Похожие презентации:
Системы массового обслуживания: понятия, примеры, модели
1.
Системы массовогообслуживания: понятия, примеры,
модели
2.
Система массового обслуживания• Система массового обслуживания
(СМО) — это система, в которой есть хотя
бы один канал обслуживания, поток заявок
и поток обслуживаний.
• Большой класс систем, которые сложно
изучить аналитическими способами, но
которые хорошо изучаются методами
статистического моделирования, сводится к
системам массового обслуживания (СМО).
3.
СМО• Каждая СМО состоит из определенного
числа обслуживающих единиц (приборов,
устройств, пунктов, станций), которые
будем называть каналами обслуживания.
Каналами могут быть линии связи, рабочие
точки, вычислительные машины, продавцы
и др. По числу каналов СМО подразделяют
на одноканальные и многоканальные.
4.
СМООбслуживание — это непосредственное взаимодействие с клиентом,
которое направлено на удовлетворение его спроса.
Системой массового обслуживания (СМО) называется система, в
которой:
• возникает массовые требования на выполнения каких-либо видов
услуг
• происходит удовлетворение этих требований — обслуживание
Главной особенностью процессов массового обслуживания является их
случайность. Выделяются две взаимодействующие стороны, одна из
которых обслуживает, а вторая выступает в качестве обслуживаемой.
Присутствие случайности в поведении одной из сторон приводит к
случайному протеканию всего процесса обслуживания. Причины
случайности заключаются в массовом характере потребностей, а также
в случайности работы обслуживающей системы.
5.
СМОПредметом теории массового обслуживания является
построение математических моделей, связывающих
заданные условия работы СМО (число каналов, их
производительность, характер потока заявок и т.п.) с
показателями эффективности СМО, описывающими ее
способность справляться с потоком заявок.
В качестве показателей эффективности
СМО используются: среднее число заявок, обслуживаемых
в единицу времени; среднее число заявок в очереди;
среднее время ожидания обслуживания; вероятность
отказа в обслуживании без ожидания; вероятность того,
что число заявок в очереди превысит определенное
значение и т.п.
6.
СМОСМО делят на два основных типа (класса): СМО с
отказами и СМО с ожиданием (очередью). В СМО с отказами
заявка, поступившая в момент, когда все каналы заняты,
получает отказ, покидает СМО и в дальнейшем процессе
обслуживания не участвует (например, заявка на телефонный
разговор в момент, когда все каналы заняты, получает отказ и
покидает СМО необслуженной). В СМО с ожиданием заявка,
пришедшая в момент, когда все каналы заняты, не уходит, а
становится в очередь на обслуживание.
СМО с ожиданием подразделяются на разные виды в
зависимости от того, как организована очередь: с
ограниченной или неограниченной длиной очереди, с
ограниченным временем ожидания и т.п.
7.
СМО• Примерами СМО могут служить:
автобусный маршрут и перевозка
пассажиров; производственный конвейер
по обработке деталей; влетающая на чужую
территорию эскадрилья самолетов, которая
«обслуживается» зенитками ПВО; ствол и
рожок автомата, которые «обслуживают»
патроны; электрические заряды,
перемещающиеся в некотором устройстве
и т. д.
8.
СМОПримеры процессов массового обслуживания
• обслуживание покупателей в сфере
мелкооптовой и розничной торговли;
• транспортное обслуживание;
• работа телекоммуникационных сетей;
• медицинское обслуживание;
• гостиничный бизнес;
• обслуживание в бистро, кафе, ресторанах;
• обработка документов в системе управления;
• туристический бизнес и многие др.
9.
СМО• Заявки поступают в СМО обычно не регулярно,
а случайно, образуя так
называемый случайный поток заявок
(требований). Обслуживание заявок, вообще
говоря, также продолжается какое-то
случайное время. Случайный характер потока
заявок и времени обслуживания приводит к
тому, что СМО оказывается загруженной
неравномерно: в какие-то периоды времени
скапливается очень большое количество заявок
(они либо становятся в очередь, либо покидают
СМО необслуженными), в другие же периоды
СМО работает с недогрузкой или простаивает.
10.
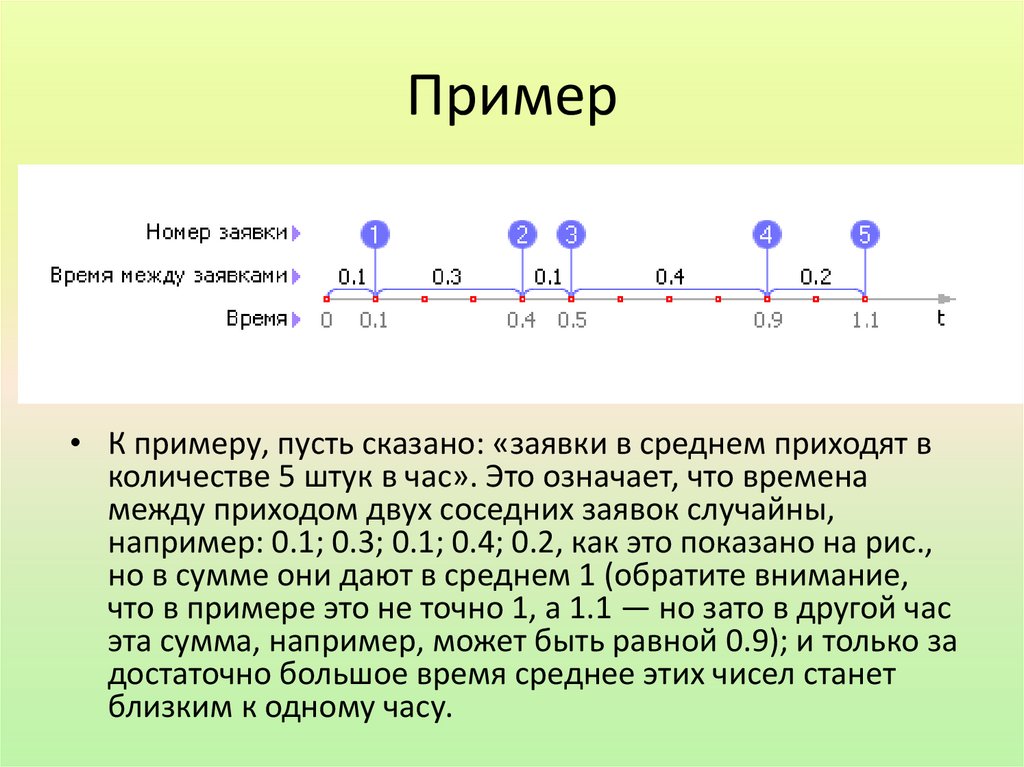
Пример• К примеру, пусть сказано: «заявки в среднем приходят в
количестве 5 штук в час». Это означает, что времена
между приходом двух соседних заявок случайны,
например: 0.1; 0.3; 0.1; 0.4; 0.2, как это показано на рис.,
но в сумме они дают в среднем 1 (обратите внимание,
что в примере это не точно 1, а 1.1 — но зато в другой час
эта сумма, например, может быть равной 0.9); и только за
достаточно большое время среднее этих чисел станет
близким к одному часу.
11.
• Результат (например, пропускнаяспособность системы), конечно, тоже будет
случайной величиной на отдельных
промежутках времени. Но измеренная на
большом промежутке времени, эта
величина будет уже, в среднем,
соответствовать точному решению. То есть
для характеристики СМО интересуются
ответами в статистическом смысле.
12.
Система массового обслуживания считается заданной, еслиопределены:
1) входящий поток требований, или, иначе говоря, закон
распределения, характеризующий моменты времени
поступления требований в систему. Первопричину требований
называют источником. В дальнейшем условимся считать, что
источник располагает неограниченным числом требований и
что требования однородны, т. е. различаются только
моментами появления в системе;
2) система обслуживания, состоящая из накопителя и узла
обслуживания. Последний представляет собой одно или
несколько обслуживающих устройств, которые в дальнейшем
будем называть приборами. Каждое требование должно
поступить на один из приборов, чтобы пройти обслуживание.
Может оказаться, что требованиям придется ожидать, пока
приборы освободятся. В этом случае требования находятся в
накопителе, образуя одну или несколько очередей. Положим,
что переход требования из накопителя в узел обслуживания
происходит мгновенно;
13.
Система массового обслуживаниясчитается заданной, если
определены:
3) время обслуживания требования каждым прибором, которое
является случайной величиной и характеризуется некоторым законом
распределения;
4) дисциплина ожидания, т. е. совокупность правил,
регламентирующих количество требований, находящихся в один и тот
же момент времени в системе. Система, в которой поступившее
требование получает отказ, когда все приборы заняты, называется
системой без ожидания. Если требование, заставшее все приборы
занятыми, становится в очередь и ожидает до тех пор,
пока освободиться один из приборов, то такая система называется
чистой системой с ожиданием. Система, в которой требование,
заставшее все приборы занятыми, становится в очередь только в том
случае, когда число требований, находящихся в системе, не превышает
определенного уровня (в противном случае происходит потеря
требования), называется смешанной системой обслуживания;
14.
Система массового обслуживаниясчитается заданной, если
определены:
5) дисциплина обслуживания, т. е. совокупность правил, в
соответствии с которыми требование выбирается из очереди для
обслуживания. Наиболее часто на практике используются следующие
правила:
- заявки принимаются к обслуживанию в порядке очереди;
- заявки принимаются к обслуживанию по минимальному времени
получения отказа;
- заявки принимаются к обслуживанию в случайном порядке в
соответствии с заданными вероятностями;
6) дисциплина очереди, т.е. совокупность правил, в соответствии с
которыми требование отдает предпочтение той или иной очереди
(если их не сколько) и располагается в выбранной очереди.
Например, поступившее требование может занять место в самой
короткой очереди; в этой очереди оно может расположиться
последним (такая очередь называется упорядоченной), а может
пойти на обслуживание вне очереди. Возможны и другие варианты.
15.
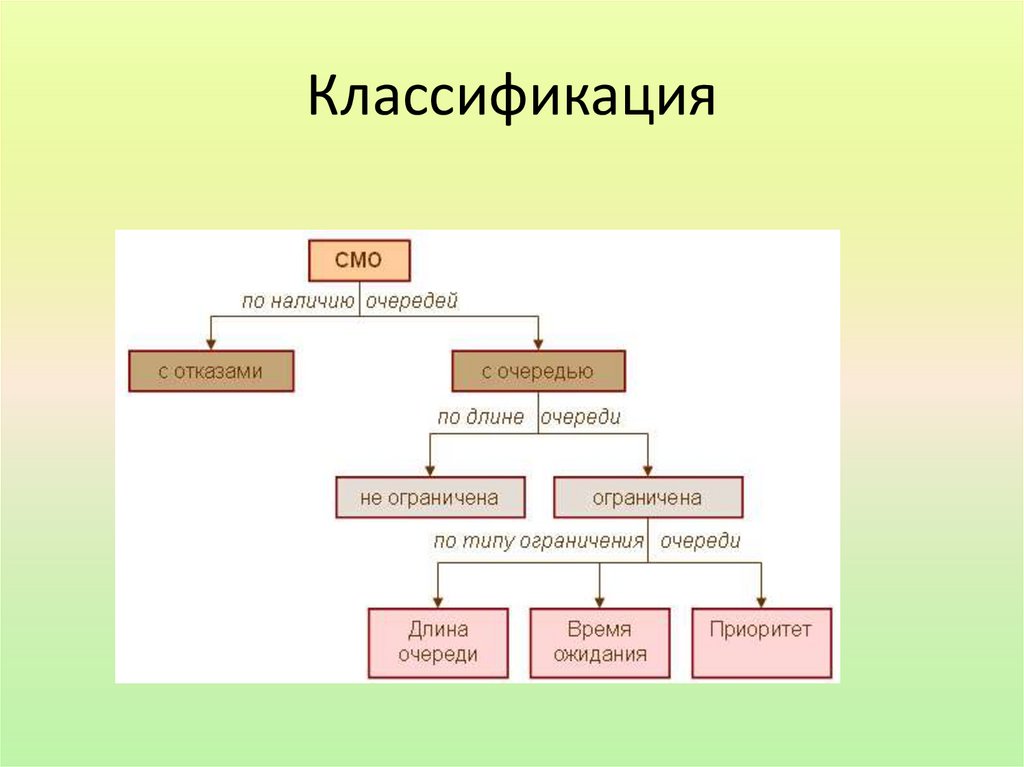
Классификация систем массовогообслуживания
СМО могут быть двух видов:
♦ СМО с отказами;
♦ СМО с ожиданием (т. е. с очередью).
Обслуживание в системах с очередью может
иметь различный характер:
Ø обслуживание может быть упорядоченным;
Ø обслуживание в случайном порядке;
Ø обслуживание с приоритетом, при этом
приоритет может быть с прерыванием и без
прерывания.
16.
Системы с очередью делятся на:• системы с неограниченным ожиданием, при
этом поступившая в СМО задача становится в
очередь и ждет обслуживания. Рано или
поздно она будет обслужена;
• системы с ограниченным ожиданием, при
этом на заявку в очереди накладываются
ограничения, например ограниченное время
пребывания в очереди, длина очереди, общее
время пребывания в СМО. В зависимости от
типа СМО для оценки эффективности могут
быть применены разные показатели.
17.
Классификация• Для СМО с отказами используются следующие
показатели эффективности:абсолютная
пропускная способность А – среднее число
заявок, которое может быть обслужено в
единицу времени;
• относительная пропускная способность Q –
относительное среднее число заявок. При этом
относительную пропускную способность
можно найти по формуле
Q=A/ λ
где λ – это интенсивность поступления заявок в
СМО.
18.
КлассификацияДля СМО с ожиданием абсолютная пропускная
способность А и относительная пропускная
способность Q теряют смысл, но важными
становятся другие характеристики:
Ø единица времени ожидания в очереди;
Ø среднее число заявок в очереди;
Ø среднее время пребывания в системе.
Для СМО с ограниченной очередью интересны
обе группы характеристик.
19.
Классификация20.
Описание моделиНа вход n-канальной СМО с m-очередью поступает простейший поток заявок с
интенсивностью λi в зависимости от состояния системы.
Интенсивность простейшего потока обслуживания каналом или каналами μi в
зависимости от состояния системы.
Если заявка застаёт все каналы свободными, то она принимается на
обслуживание и обслуживается одним из n каналов.
После окончания обслуживания один канал освобождается.
Если вновь прибывшая заявка застаёт в системе свободным хотя бы один
канал, то она принимается на обслуживание одним из свободных каналов и
обслуживается до конца.
Если заявка застаёт все каналы занятыми, то она становится в очередь и
«терпеливо» ждёт своего обслуживания.
Дисциплина очереди естественная: кто раньше пришёл, тот раньше и
обслуживается. Максимальное число мест в очереди m.
Если вновь прибывшая заявка застаёт в очереди m-заявок, то она получает
отказ и исключается из обслуживания.
Состояние рассмотренной системы будем связывать с числом заявок,
находящихся в системе.
21.
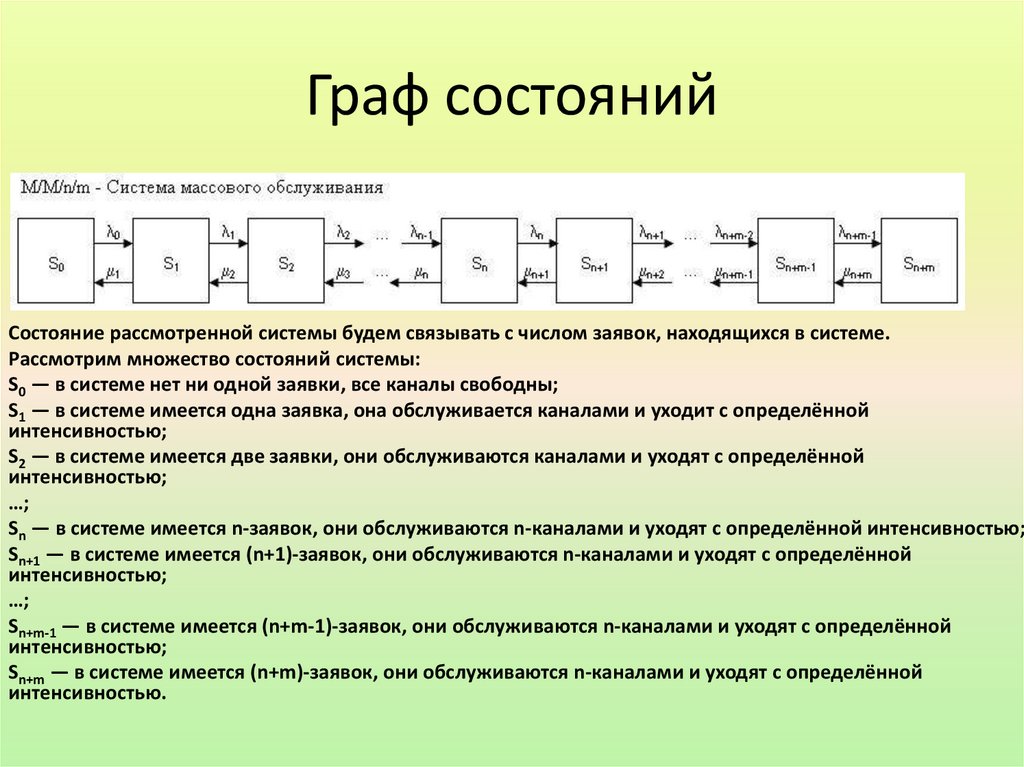
Граф состоянийСостояние рассмотренной системы будем связывать с числом заявок, находящихся в системе.
Рассмотрим множество состояний системы:
S0 — в системе нет ни одной заявки, все каналы свободны;
S1 — в системе имеется одна заявка, она обслуживается каналами и уходит с определённой
интенсивностью;
S2 — в системе имеется две заявки, они обслуживаются каналами и уходят с определённой
интенсивностью;
…;
Sn — в системе имеется n-заявок, они обслуживаются n-каналами и уходят с определённой интенсивностью;
Sn+1 — в системе имеется (n+1)-заявок, они обслуживаются n-каналами и уходят с определённой
интенсивностью;
…;
Sn+m-1 — в системе имеется (n+m-1)-заявок, они обслуживаются n-каналами и уходят с определённой
интенсивностью;
Sn+m — в системе имеется (n+m)-заявок, они обслуживаются n-каналами и уходят с определённой
интенсивностью.
22.
Система дифференциальныхуравнений
• Система дифференциальных уравнений,
описывающих поведение системы, имеет вид:




















 Математика
Математика








