Анализ прохождения сигналов через линейные цепи. Урок 7

1. ТЕМА 7 АНАЛИЗ ПРОХОЖДЕНИЯ СИГНАЛОВ ЧЕРЕЗ ЛИНЕЙНЫЕ ЦЕПИ

2. ЛЦ С ПОСТОЯННЫМИ ПАРАМЕТРАМИ

При прохождении любых сигналов через ЛЦ с постоянными
параметрами изменяется их форма за счёт ослабления или
усиления составляющих их спектра в зависимости от частоты,
что
приводит
к
линейным
частотным
искажениям.
Количественная оценка таких изменений выполняется путём
применения методов анализа, в принципе, пригодных для любого
типа ЛЦ.
Существуют четыре основных метода: классический; временной;
спектральный; операторный. Все они, КРОМЕ классического,
используют принцип суперпозиции, т. е.:
1 – входной сигнал разбивается на сумму элементарных
сигналов: коротких импульсов – во временном методе;
гармонических
колебаний
–
в
спектральном
методе;
гармонических колебаний, затухающих по экспоненте – в
операторном методе;
2 – с помощью той или иной характеристики цепи находится
отклик на каждый элементарный сигнал;
3 – определяется сумма откликов, представляющая собой
выходной сигнал.

3. КЛАССИЧЕСКИЙ МЕТОД (МЕТОД ДИФФ. УРАВНЕНИЙ)

• Основан на том, что по законам Кирхгофа составляется
линейное дифференциальное уравнение n-й степени,
связывающее известную функцию входного сигнала
(воздействия) Uвх(t) и искомую функцию выходного
сигнала (реакции) Uвых(t):
dU âû õ (t )
d 2U âû õ (t )
d nU âû õ( t )
a0U âû õ (t ) a1
a2
... an
2
n
dt
dt
dt
dU âõ (t )
d 2U âõ (t )
d mU âõ (t )
b0U âõ (t ) b1
b2
... bm
2
dt
dt
dt m
где a0, a1, … an и b0, b1, … bm – для ЛЦ с постоянными
параметрами являются постоянными вещественными
коэффициентами.

4. КЛАССИЧЕСКИЙ МЕТОД (МЕТОД ДИФФ. УРАВНЕНИЙ)

Искомая функция сигнала на выходе цепи Uвых(t)
определяется в виде суммы двух функций:
Uвых(t) = Uвых1(t) + Uвых2(t),
где Uвых1(t) – частное
решение
дифференциального
уравнения, которое непосредственно зависит от вида
входного воздействия и описывает вынужденный
режим;
–
Uвых2(t) – общее решение уравнения при Uвх(t) = 0,
которое описывает переходные процессы в цепи.
• Решение дифференциального уравнения можно найти
путём использования формализованных процедур
преобразования Лапласа (операторного метода). Этот
метод используется для анализа простейших цепей,
описываемых дифференциальными уравнениями не выше
2-го порядка.

5. ВРЕМЕННОЙ МЕТОД (МЕТОД ИНТЕГРАЛА ДЮАМЕЛЯ)

• Базируется на использовании импульсной (ИХ) или
переходной (ПХ) характеристик цепи и разбиении сигнала
на короткие импульсы. Используется чаще всего для
анализа переходного режима цепи.
• ИХ обозначается h(t) и является функцией реакции цепи на
входное воздействие в виде единичной дельта-функции:
Uвх(t) = (t) и Uвых(t) = h(t) = T[ (t)].
где T – оператор цепи.
• ПХ обозначается g(t) и является функцией реакции цепи на
входное воздействие в виде единичного скачка (функции
Хевисайда):
Uвх(t) = (t) и Uвых(t) = g(t) = T[ (t)].

6. ВРЕМЕННОЙ МЕТОД (МЕТОД ИНТЕГРАЛА ДЮАМЕЛЯ)

• Так как (t )
d (t )
, то
dt
d (t ) d (T [ (t )]) dg (t )
h(t ) T [
]
dt
dt
dt
и
t
g (t ) h(t )dt
• Учитывая, что спектр дельта-функции (t) равномерный и
бесконечный, h(t) и K(j ) взаимосвязаны
преобразованиями Фурье:
1
j t
h(t )
K
(
j
)
e
d
2
K ( j ) h(t )e j t dt

7. ВРЕМЕННОЙ МЕТОД (МЕТОД ИНТЕГРАЛА ДЮАМЕЛЯ)

Для реальных цепей h(t) = 0 при t 0 и K(j ) является
аналитической функцией, то есть K(j ) = KRe( ) + jKIm( ).
Минимально-фазовая цепь - электрическая цепь, амплитудночастотная и фазо-частотная характеристика которой
определяются друг через друга однозначно.
для минимально-фазовых цепей функции KRe( ) и KIm( ) связаны
между собой преобразованиями Гильберта, поэтому достаточно
знать одну из них.
Так как Sвых(j ) = K(j ) Sвх(j ), то
t
t
0
0
U âû õ (t) h(t ) U âõ (t ) h( )U âõ (t )d h(t )U âõ ( )d
t
t
dU âõ (t )
dU âõ ( )
g (t )
d g (t )
d
d
d
0
0
- четыре вида интегралов Дюамеля.
• Недостатком метода являются существенные вычислительные
трудности нахождения интегралов свёртки для сложных функций

8. СПЕКТРАЛЬНЫЙ (ЧАСТОТНЫЙ) МЕТОД

Основан на использовании свойств передаточной частотной
характеристики (ЧХ) цепи K(j ) и известной спектральной
плотности входного сигнала Sвх(j ). Применяется для анализа
цепей в установившемся режиме. Реализуется так:
1) определение ЧХ цепи K(j );
2) определение спектра входного сигнала с помощью прямого
преобразования Фурье:
Sâõ ( j ) U âõ (t )e j t dt
3) нахождение спектра выходного сигнала:
Sâû õ ( j ) Sâõ ( j ) K ( j ) Sâõ ( ) K ( )e
j[ âõ ( ) ê ( )]
где K( ) – амплитудно-частотная характеристика (АЧХ);
к( ) – фазо-частотная характеристика (ФЧХ) цепи;
Sвх( ) и вх( ) – соответственно, модуль и фаза спектра Uвх(t).

9. СПЕКТРАЛЬНЫЙ (ЧАСТОТНЫЙ) МЕТОД

• 4) определение выходного сигнала с помощью обратного
преобразования Фурье:
1
j t
U âû õ (t )
S
(
j
)
e
d
âû
õ
2
• Этот метод широко применяется благодаря свойству
гармонических сигналов не изменять свою форму при
прохождении через ЛЦ и физической наглядности, когда
достаточно найти спектр Uвых(t), чтобы судить об
искажениях Uвх(t).
• На основе этого метода легко сформулировать требования
к неискаженной передаче сигналов: АЧХ цепи должна быть
постоянной, а ФЧХ – линейной в пределах эффективной
ширины спектра входного сигнала.

10. ОПЕРАТОРНЫЙ МЕТОД

• МЕТОД ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
Используется представление входного и выходного сигналов
преобразованиями Лапласа:
прямое преобразование –
Sâõ ( p) U âõ (t )e pt dt
0
обратное преобразование –
1
U âû õ (t )
2 j
c j
c- j
Sâû õ ( p)e pt dp
где Uвх(t), Uвых(t) и Sвх(p), Sвых(p) – соответственно, оригинал и
изображение входного и выходного сигналов; p = + j –
оператор Лапласа.
• При этом Sâû õ ( p ) Sâõ ( p ) K ( p ) ,
где K(p) – передаточная функция цепи.

11. ОПЕРАТОРНЫЙ МЕТОД

• Передаточная функция К(р) получается путем замены
переменной j на p.
• Нахождение Uвых(t) при заданном Uвх(t) и K(p) содержит три
процедуры:
– 1) преобразование Uвх(t) Uвх(p);
– 2) определение Uвых(p) = K(p)Uвх(p);
– 3) преобразование Uвых(p) Uвых(t).
• Практическое применение операторного метода ранее
упрощалось благодаря наличию таблиц прямого и
обратного преобразований Лапласа, теперь - благодаря
наличию пакетов прикладного ПО.

12. ПРОХОЖДЕНИЕ СИГНАЛОВ ЧЕРЕЗ АПЕРИОДИЧЕСКИЕ ЦЕПИ

ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ СИГНАЛОВ
Рассмотрим дифференцирующую (а) и интегрирующую (б) цепи.
C
R
i(t)
i(t)
R
Uвх(t)
Uвых(t)
Uвх(t)
а
C
Uвых(t)
б
При дифференцировании
dU âõ (t )
U âû õ (t ) 0
dt
При интегировании
1
U âû õ (t )
U âõ (t ) dt
0
0
где 0 – постоянная величина, имеющая размерность времени
для сохранения размерности исходного сигнала.

13. ПРОХОЖДЕНИЕ СИГНАЛОВ ЧЕРЕЗ АПЕРИОДИЧЕСКИЕ ЦЕПИ

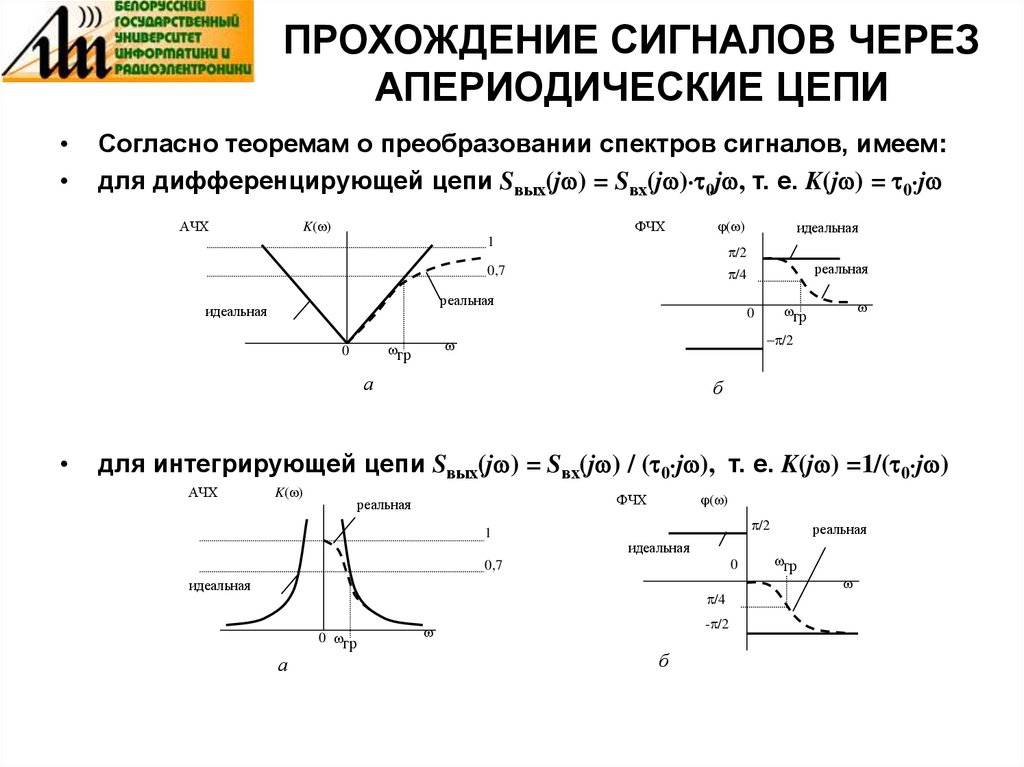
Согласно теоремам о преобразовании спектров сигналов, имеем:
для дифференцирующей цепи Sвых(j ) = Sвх(j ) 0j , т. е. K(j ) = 0 j
АЧХ
ФЧХ
K( )
/2
0,7
/4
реальная
идеальная
идеальная
реальная
гр
0
– /2
гр
0
а
( )
1
б
для интегрирующей цепи Sвых(j ) = Sвх(j ) / ( 0 j ), т. е. K(j ) =1/( 0 j )
АЧХ
K( )
( )
ФЧХ
реальная
1
/2
идеальная
0
0,7
идеальная
/4
0 гр
а
- /2
б
реальная
гр

14. АЧХ И ФЧХ ДИФФЕРЕНЦИРУЮЩЕЙ ЦЕПИ

Для дифференцирующей цепи ЧХ определяется как
U âû õ ( j )
1
K ( j )
U âõ ( j ) 1 1/( j 0 )
или при переходе от комплексных величин АЧХ будет
K ( )
1
1 1 / ( 0 ) 2
Для ФЧХ получим
где 0=RC – постоянная времени RC-цепи.
Граничная частота полосы пропускания RC-цепи гр по уровню
0,707 равна гр = 1 / 0
1
( ) arctg
0

15. АЧХ И ФЧХ ИНТЕГРИРУЮЩЕЙ ЦЕПИ

Для интегрирующей цепи ЧХ определяется как
U âû õ ( j )
1
K ( j )
U âõ ( j ) 1 j 0
или при переходе от комплексных величин АЧХ будет
K ( )
Для ФЧХ получим
1
1 ( 0 ) 2
( ) arctg( 0 )
где 0=RC – постоянная времени RC-цепи.
Таким образом, рассмотренные цепи могут осуществлять
процесс приближенного дифференцирования входного сигнала
при условии fв<<fгр
( fв– верхняя частота в спектре сигнала, f гр 1 / 2 0 )
и интегрирования при fв>>fгр.

16. ПРОХОЖДЕНИЕ ПРЯМОУГОЛЬНОГО ИМПУЛЬСА ЧЕРЕЗ ДЦ И ИЦ

Для прямоугольного импульса с амплитудой Е напряжения на
элементах RC-цепи изменяются как
U R (t ) Ee
t / 0
U C (t ) E 1 e
E
0,9E
Uс(t)
0,63
UR(t)
0,1E
0
0
• Время нарастания – tн = 2,3 0 .
2,3 0
t
t / 0

17. ПРОХОЖДЕНИЕ ПРЯМОУГОЛЬНОГО ИМПУЛЬСА ЧЕРЕЗ ДЦ И ИЦ

Для прямоугольного импульса с амплитудой Е напряжения на
элементах RC-цепи изменяются как
U R (t ) Ee
t / 0
U C (t ) E 1 e
E
0,9E
Uс(t)
0,63
UR(t)
0,1E
0
0
• Время нарастания – tн = 2,3 0 .
2,3 0
t
t / 0

18. ПРОХОЖДЕНИЕ ПРЯМОУГОЛЬНОГО ИМПУЛЬСА ЧЕРЕЗ ДЦ И ИЦ

Представим входной прямоугольный импульс в виде
U(t) = E[1(t) – 1(t – tи)].
Из теории цепей известно, что импульсная характеристика для
дифференцирующей RC-цепи
h(t ) (t )
1
0
e t / 0 1(t )
Тогда, по методу интеграла Дюамеля, выходной сигнал
1 t / 0
U вых (t ) U вх ( )h(t )d E 1( ) 1( tи ) (t ) e
d
0
0
0
t
t
Ee t / 0 1(t ) Ee( t и ) / 0 1(t и ) .
Напряжение на резисторе
0, t 0;
t / 0
U R (t ) Ee
, 0 t и;
Ee t / 0 Ee (t и ) / 0 , t .
и

19. ПРОХОЖДЕНИЕ ПРЯМОУГОЛЬНОГО ИМПУЛЬСА ЧЕРЕЗ ДЦ И ИЦ

Представим входной прямоугольный импульс в виде
U(t) = E[1(t) – 1(t – tи)].
Для интегрирующей RC-цепи импульсная характеристика равна
h(t )
Выходной сигнал
t
t / 0
1 t /
0 d
U âû õ (t ) E 1( ) 1( è ) e
τ
0
0
E 1 e
1 t / 0
e
1(t )
0
1(t ) E 1 e
Напряжение на конденсаторе
( t è ) / 0
1(t ) .
è
0, t 0;
t / 0
UC (t ) E (1 e
), 0 t è ;
t / 0
(t è ) / 0
E
(1
e
)
E
(1
e
), t è .

20. ПРОХОЖДЕНИЕ ПРЯМОУГОЛЬНОГО ИМПУЛЬСА ЧЕРЕЗ ДЦ И ИЦ

Uвх(t)
Uвх(t)
E
E
а
а
0
Uвых(t)
E
0,9Е
б
0
и
01
Uвых(t)
E
0,9Е
02 03
б
0,1Е
0
и
и1
и2
01
< 02< 03
и
t
01
02
03
t
01
02
03
t
01
02
03
0,1Е
и
0
и1
t
и2
и3
01
< 02< 03

21. ПРОХОЖДЕНИЕ ПРЯМОУГОЛЬНОГО ИМПУЛЬСА ЧЕРЕЗ ДЦ И ИЦ

Форма сигнала на выходе дифференцирующей RC-цепи тем
ближе к производной от входного сигнала, чем меньше значение
0 1/(2 fâ ) fâ 1/ è
0 в сравнении с и или когда
,
Эта цепь как бы “укорачивает” импульсный сигнал.
При fв>>fгр цепь не оказывает влияния на сигнал за исключением
устранения постоянной составляющей и используется в качестве
разделительной цепи по постоянному току.
Форма сигнала на выходе интегрирующей RC-цепи тем ближе
к интегралу от входного сигнала,
0 1/(2 чем
fâ ) больше
fâ 1/ è значение 0 в
сравнении с и или когда
,
Эта цепь как бы “удлиняет” импульсный сигнал.
При fв<<fгр , ( 0 / и 0,03) выходной сигнал близок к входному
Аналогичные результаты можно получить, используя RL-цепи.
Так, заменяя C на L, соответственно получим интегрирующую и
дифференцирующую RL-цепи.
.