Похожие презентации:
Рівновеликі многокутники. 8 клас
1.
Прензентація до урокугеометрії у 8 класі.
Гордієнко Т.М.
2.
ЧОМУ РІВНОВЕЛИКІ ФІГУРИВВАЖАЮТЬСЯ
РІВНОСКЛАДЕНИМИ?
3.
1 ІСНУЮТЬ РІВНОВЕЛИКІ ФІГУРИ;2 РІВНОВЕЛИКІ ФІГУРИ Є
РІВНОСКЛАДЕНИМИ;
3 БУДЬ ЯКУ ФІГУРУ МОЖНА ШЛЯХОМ
РОЗРІЗАННЯ ПЕРЕКРОІТИ У
РІВНОВЕЛИКУ ЇЙ ФІГУРУ,НАПРИКЛАД У
КВАДРАТ,АБО ПАРАЛЕЛОГРАМ
4.
Вершина С трикутника АВС з основою АВрухається по прямій, паралельній стороні АВ. При
цьому отримуємо різні трикутники. Деякі з них ми
бачимо на малюнку.
Чи будуть ці трикутники рівновеликі?
5.
Площа S цих трикутників приймає одній ті самі значення, так як всі трикутники
зі спільною основою и рівними
висотами.
Фігури, які мають рівну площу
називають рівновеликими.
6.
Рівновеликі фігури - плоскі фігури однієїплощі, або геометричні тіла з одинаковими
об’ємами. Приклади:
а=8
в=2
а=4
S=16
S=16
7.
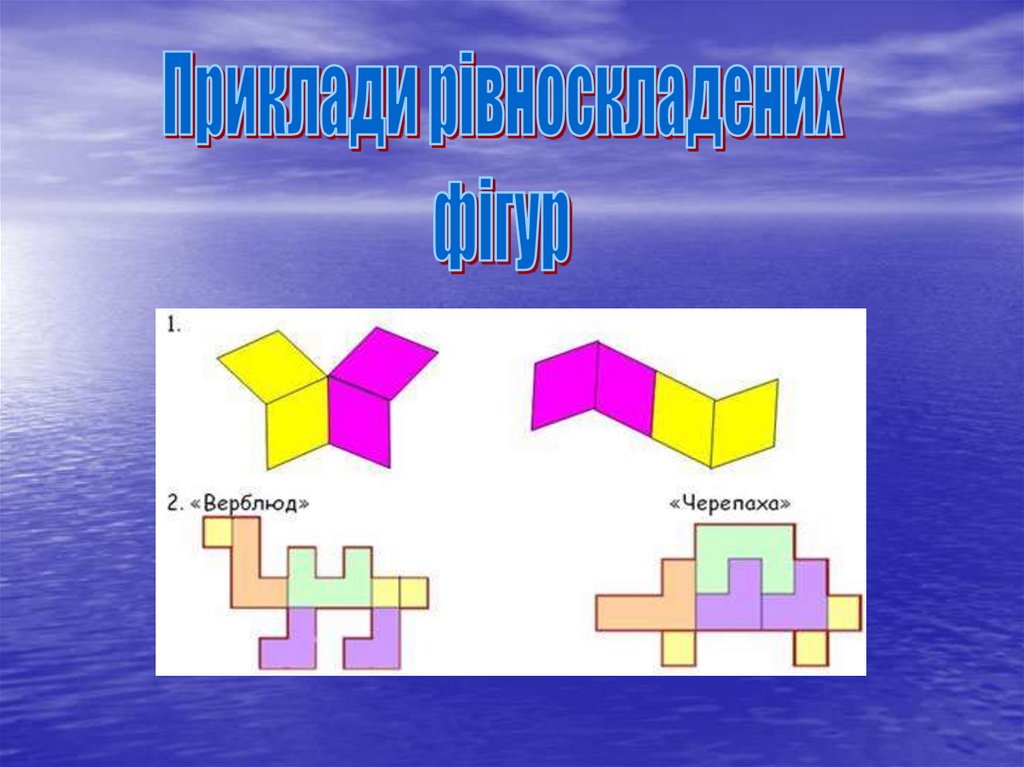
це фігури, які можна розрізати на однакове числорівних часттн.. Рівноскладені фігури є
рівновеликими. Угорський математик Я. Больяй
(1832) і німецький математик П. Гервін (1833)
довели, що рівновеликі многокутники являються
рівноскладеними (теорема Больяй - Гервіна). Тому
розрізанням на частини і перекладанням цих частин
можна будь-який многокутник перетворити у
рівновеликий йому квадрат.
8.
9.
Всякий многокутник можнарозрізати на деяке число
трикутників.
10.
• Медіана разбиває трикутник на дватрикутника однакової площі.
• Медіани трикутника перетинаються в одній
точці, яка ділить кожну з них у відношенні
2:1, рахуючи від вершини. Ця точка
називається центром ваги трикутника.
• Весь трикутник ділиться своїми медіанами на
шість рівновеликих трикутників.
11.
Точку перетину медіан трикутниканазивабть центром ваги або
центром мас. Виявляється, якщо
помістити в вершини трикутника
рівні маси, то їх центр попаде в цю
точку. Центр рівних мас іноді
називають центроідом. В цій же
точці розміщується і центр мас
однорідної трикутної пластинки.
Якщо подібну пластинку помістити
на шпильку так, щоб гострий кінець
останньої попав точно в центроід, то
пластинка буде знаходитися у
равновазі.Спробуйте зробити це
самі і переконайтеся в
справедливості даного твердждення.
12.
• Чи можна перекроїти квадрат у будь-якийбажаний многокутник тої ж площини або, що
те саме, будь-який многокутник перекроїти у
рівновеликий йому квадрат?
• Відповідь: Так!
• Дуже важливе твердження. Всякий
многокутник можна претворити в
рівновеликий йому квадрат.
Доведенням може служити яка-небудь
можлива послідовність перетворень
многокутника у квадрат.
13. Всякий трикутник рівноскладений з деяким паралелограмом
14.
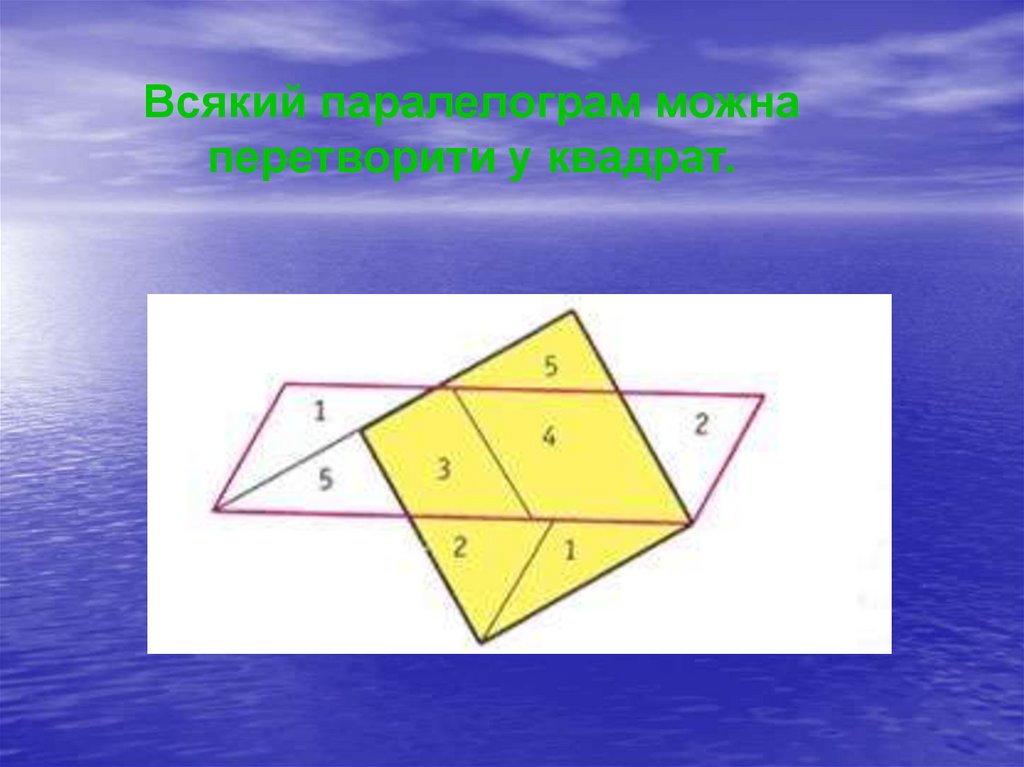
Всякий паралелограм можнаперетворити у квадрат.
15.
Спробуй самстворити
перетворення
фігур













 Математика
Математика








