Похожие презентации:
Квантовая механика. Лекция 5
1.
Квантовая механикаЛекция 5
h
l = mV
2.
Идея корпускулярно-волнового дуализмаматерии – Луи де Бройль (1892-1987)
2
3.
В 1923 году французский физик Луи де Бройльвыдвинул гипотезу об универсальности
корпускулярно-волнового дуализма: не только
фотоны, но и электроны и любые другие частицы
материи наряду с корпускулярными обладают также и
волновыми свойствами.
Согласно де Бройлю, с каждым микрообъектом
связаны, с одной стороны, корпускулярные
характеристики – энергия E и импульс p, а с другой
стороны, волновые характеристики – частота ν и
длина волны λ.
3
4.
Корпускулярные и волновыехарактеристики микрообъектов связаны
такими же количественными
соотношениями, как и у фотона:
E = h ; E = p c m c
2
2 2
2 4
E h h
для фотона m = 0 p = =
=
c
c
l
h
для частицы m 0 l =
p
4
5.
56.
Самый важный вопрос о волнах де Бройля6
7.
Первое экспериментальное подтверждениегипотезы де Бройля было получено в 1927 году
американскими физиками К. Девиссоном и
Л. Джермером. Они обнаружили, что пучок
электронов, рассеивающийся на кристалле никеля,
дает дифракционную картину.
В этих экспериментах кристалл играл роль
естественной дифракционной решетки. По
положению дифракционных максимумов была
определена длина волны электронного пучка,
которая оказалась в полном соответствии с формулой
де Бройля.
7
8.
Эксперименты Дэвиссона-Джермера8
9.
В 1928 году английский физикДж. Томсон наблюдал дифракционную
картину, возникающую при
прохождении пучка электронов с
энергией~10 кэВ через тонкую (0.1 мкм)
фольгу из золота. На фотопластинке
наблюдались концентрические светлые
и темные кольца, радиусы которых
менялись с изменением скорости
электронов (т. е. длины волны) согласно
де Бройлю.
9
10.
11.
Электронный микроскоп — прибор,позволяющий получать изображение
объектов с максимальным увеличением
до 106 раз, благодаря использованию
вместо светового потока пучка электронов
с энергиями 200 эВ — 400 кэВ и более
(просвечивающие – до 1 МэВ).
Разрешающая способность электронного
микроскопа в 1000—10000 раз превосходит
разрешение традиционного светового
микроскопа и для лучших современных
приборов может быть меньше одного
ангстрема.
1932 году М. Кнолль и Э. Руска
11
12.
Использование открытия де Бройля дляописания атома
12
13.
Как описать частицы?Частицы обладают волновыми свойствами.
Простейшей волной с частотой ω и
волновым вектором κ является плоская
монохроматическая волна- плоская волна
де Бройля
i ( wt kr )
(r , t ) = Ae
( i / )( Et pr )
(r , t ) = Ae
13
14.
максимумы в картине дифракцииэлектронов соответствуют наибольшей
интенсивности волн де Бройля.
Ψ -функция характеризует состояние
микрочастицы
Физический смысл волн де Бройля- это
волны вероятности. Вероятность
нахождения частицы в интервале от х до
x+dx
2
( х) dx = P
14
15.
Статистическая интерпретацияПринципиально невозможно предсказать,
куда попадет очередной электрон после
рассеяния, существует лишь определенная
вероятность попадания электрона в то или
иное место.
Таким образом, описание состояния
микрообъекта и его поведения может быть
дано только на основе понятия вероятности.
15
16.
Корпускулярно-волновой дуализм.Статистическая интерпретация.
1. Микрочастица сочетает в себе свойства
и частицы и волны.
2. Движение микрочастиц носит
вероятностный характер.
3. Классические представления о
движении неприменимы. Понятие
траектории неприменимо.
16
17.
Pm
Z
r
X
Y
18.
19.
Микрочастица – это образование особого рода:частица+волна.
Необходимость построения непротиворечивой
теории, объясняющей процессы, происходящие в
микромире. За короткий период с июня 1925-го года
и по июнь 1926-го года, были опубликованы сразу
три оригинальных и независимо сделанных
варианта полной квантовой теории.
– матричная квантовая механика Вернера
Гейзенберга (1901-76).
– волновая механика
Эрвина Шредингера
(1887-1961).
– квантовая алгебра Пауля Дирака (1902 1984).
19
20.
Принцип неопределенностейГейзенберга (1927 г.)
В.Гейзенберг выдвинул идею о
принципиальной невозможности
измерения определенных пар связанных между
собой характеристик частицы так, чтобы они
одновременно имели точные значения.
Микрочастица не может иметь одновременно
точных значений координат (x,y,z)и компонентов
импульса ( p x , p y , pz ), а также энергии некоторого
состояния частицы и промежутка времени, в
течение которого оно существует.
20
21.
Принцип неопределенностейГейзенберга
Пары канонически сопряженных величин
(динамические переменные):
1) Координаты и импульс
2) E-энергия и t-время
Соотношения неопределенностей
x p x
y p y
Е t
z p z
Произведение неопределенностей двух сопряженных
переменных не может быть по порядку величины меньше
постоянной Планка.
21
22.
Стационарные состояния электронав атоме
Если бы электрон упал на ядро, его координата и
импульс одновременно имели бы точное значение,
что несовместимо с принципом неопределенности
e2
2
e2
p2
k
k =
r p = E =
2
r
r 2mr
2m
2
2
e
E
k 2 =0
= 2
3
r
2mr
r
4
2
2
k me
; Emin =
rmin =
2
2
2
kme
22
23.
Принцип дополнительностиВ 1927 году Н. Бор сформулировал принципиальное
положение квантовой механики – принцип
дополнительности, согласно которому получение
экспериментальной информации об одних физических
величинах, описывающих микрообъект, неизбежно связано с
потерей информации о некоторых других величинах,
дополнительных к первым.
В соответствии с принципом дополнительности волновое и
корпускулярное описания микропроцессов не исключают и
не заменяют, а дополняют друг друга. Для формирования
представления о микрообъекте необходим синтез этих двух
описаний.
23
24.
25.
Состояние микрочастицы описывается в квантовоймеханике волновой функцией Ψ, являющейся
функцией координат и времени и может быть
найдена путем решения уравнения:
U = i
2m
t
Это уравнение было установлено Шредингером в 1926
г. называется общим уравнением Шредингера.
i – мнимая единица, m – масса частицы, - оператор
Лапласа, U – потенциальная энергия частицы
25
26.
= (x , y, z)E
U
- оператор Лапласа
= 2 2 2
x
y
z
2
2
2
27.
Волновая функция и ее статистический смыслВероятность нахождения частицы в момент времени t в
области пространства с координатами определяется
интенсивностью волновой функции.
2
dP = dV
- комплексная функция, а вероятность всегда
действительная и положительная величина, то за меру
интенсивности принимают квадрат модуля волновой
функции
dP
2
=
=
Плотность вероятности
dV
Вероятность
2
P = dP = dV
V
V
( x, y, z, t ) dV = 1
2
27
28.
Волновая функция – объективная характеристикасостояния микрочастицы. Она должна быть:
1. Конечной
2. Однозначной
3. Непрерывной
Среднее значение физической величины,
характеризующей микрообъект, находящийся в
состоянии, описываемом волновой функцией Ψ,
L = L dV = L dV
2
28
29.
Уравнение Шредингера29
30.
Волны де Бройля30







































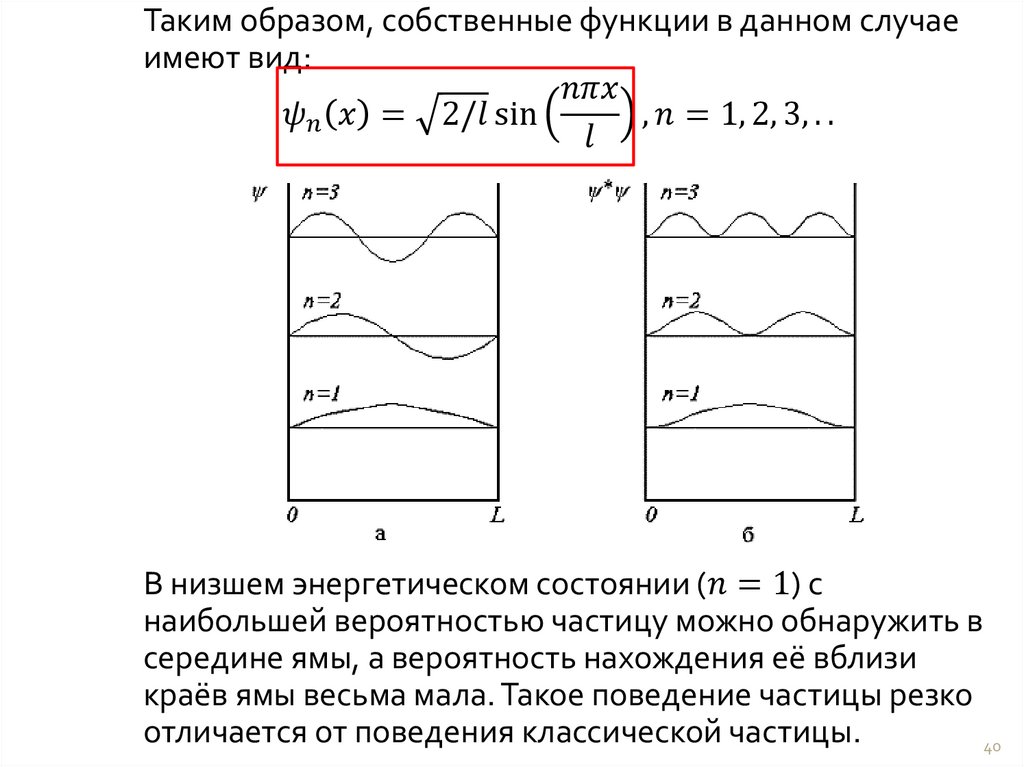





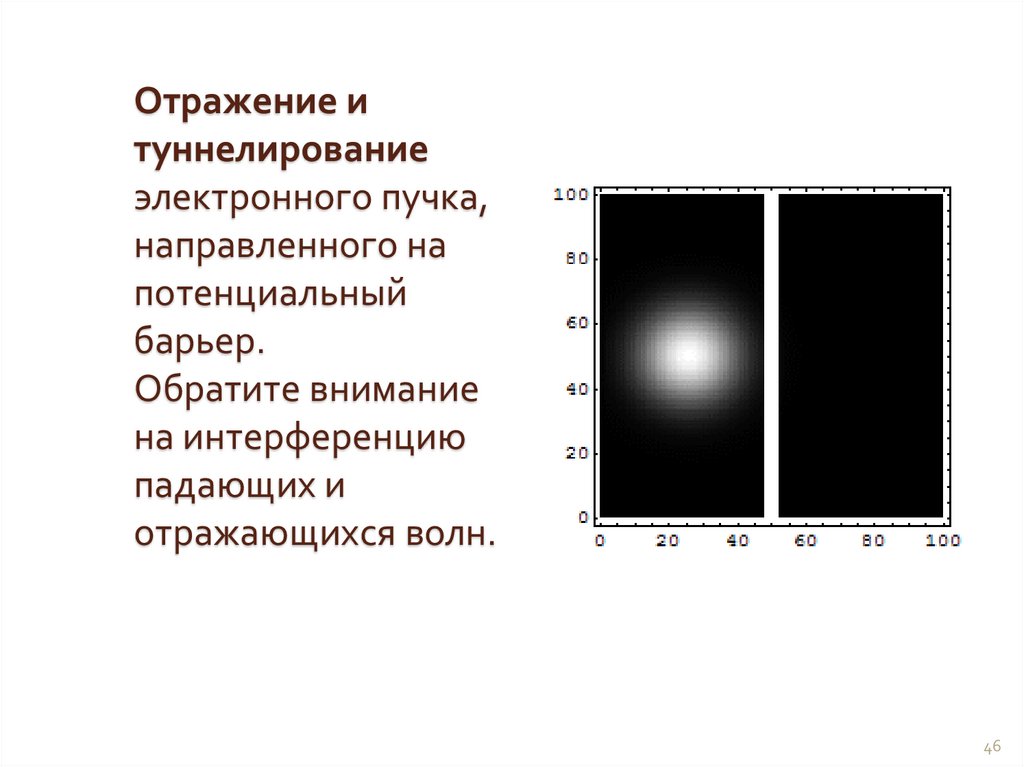















 Физика
Физика








