Квантовая механика

1.

Объясняет поведение микрочастиц,
обладающих волновыми свойствами.
В основе квантовой механики:
гипотеза де Бройля,
соотношение неопределенностей Гейзенберга,
уравнение Шредингера.

2.

Луи де Бройль (1892 - 1987) , Франция;
Вернер Гейзенберг (1901-1975), Германия;
Эрвин Шредингер ( 1887-1961), Австрия.

3.

Гипотеза де Бройля (1923 г.)
Корпускулярно-волновой дуализм универсален: соотношения, выполняющиеся для
фотонов
h , p
h
,
справедливы и для частиц , имеющих
массу покоя.

4.

Любой частице,
обладающей
импульсом p ,
сопоставляется волновой
процесс с длиной волны
h
.
p

5.

Для классической частицы
p m ,
c
для релятивистской частицы
p
m0
1
2
c
2
.
~ c

6.

Рассеяние электронов монокристаллом
никеля
Электронная пушка
Клинтон Дэвиссон,,Лестер Джермер (1927 г.)
U уск
V
G
Ni
Цилиндр
Фарадея

7.

2
p
eU уск ;
2m
p 2meU уск ;
h
;
2meU уск
2d sin n , n 1,2,...
const
угол скольжения;
U уск n / 2d sin me nD.

8.

Зависимость силы тока от ускоряющего
напряжения
Сила тока I
определяется
I
числом электронов,
отраженных от кристалла.
U уск nD
0
D
D
U уск
Максимумы кривой отстоят друг от друга
на одинаковых расстояниях.

9.

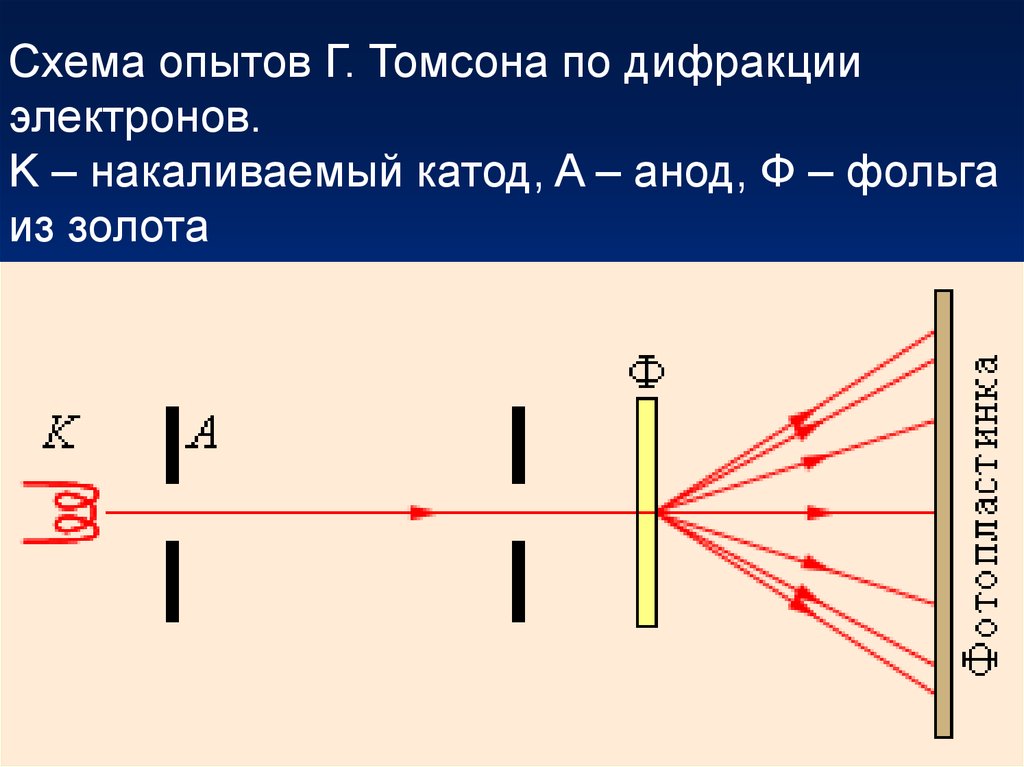
Схема опытов Г. Томсона по дифракции
электронов.
K – накаливаемый катод, A – анод, Ф – фольга
из золота

10.

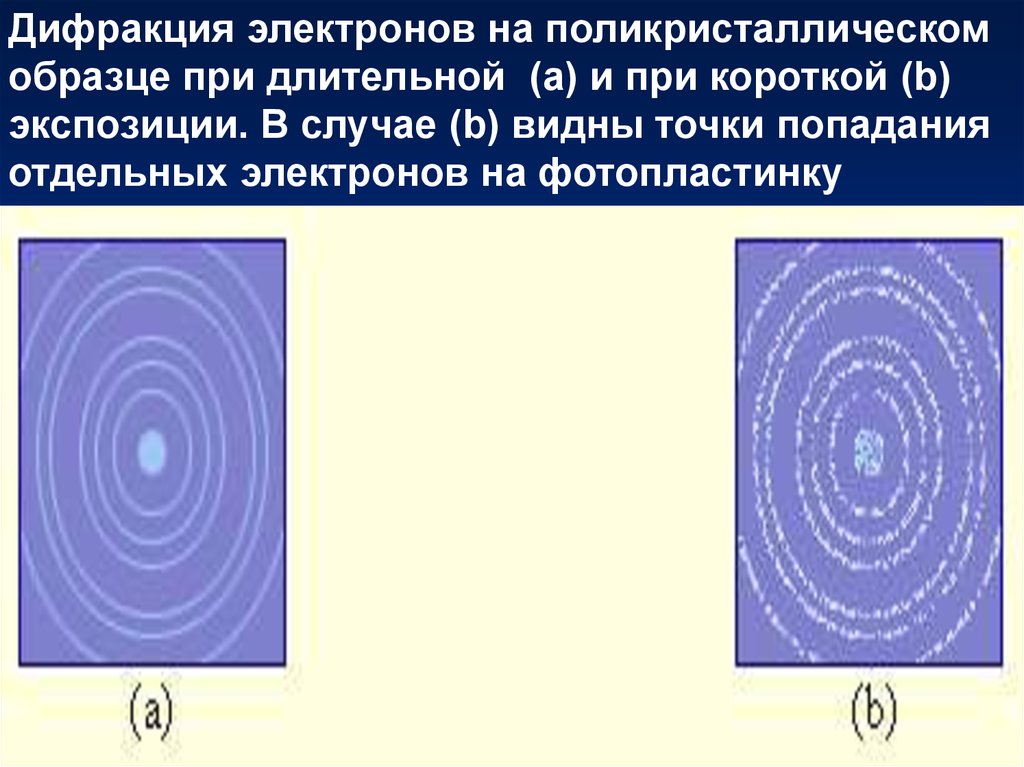
Дифракция электронов на поликристаллическом
образце при длительной (a) и при короткой (b)
экспозиции. В случае (b) видны точки попадания
отдельных электронов на фотопластинку

11.

Свойства волн де Бройля:
1) имеют специфическую квантовую
природу, нет аналогии с волнами в
классической физике;
x, y, z, t
2) волновая функция
используется для расчета вероятности
нахождения частицы в данной точке
пространства в данный момент времени;

12.

3) интенсивность волн де Бройля
определяет квадрат модуля
2
функции
;
4) фазовая скорость волн де Бройля
для классической частицы, движущейся
со скоростью
:
W
m
ф
;
k
k
p
2m
2
2

13.

5) групповая скорость волн де Бройля:
d d dW d p p
.
u
dk d k dp dp 2m m
2
Использованы обозначения:
циклическая частота,
k – волновое число,
h
2
постоянная Планка.

14.

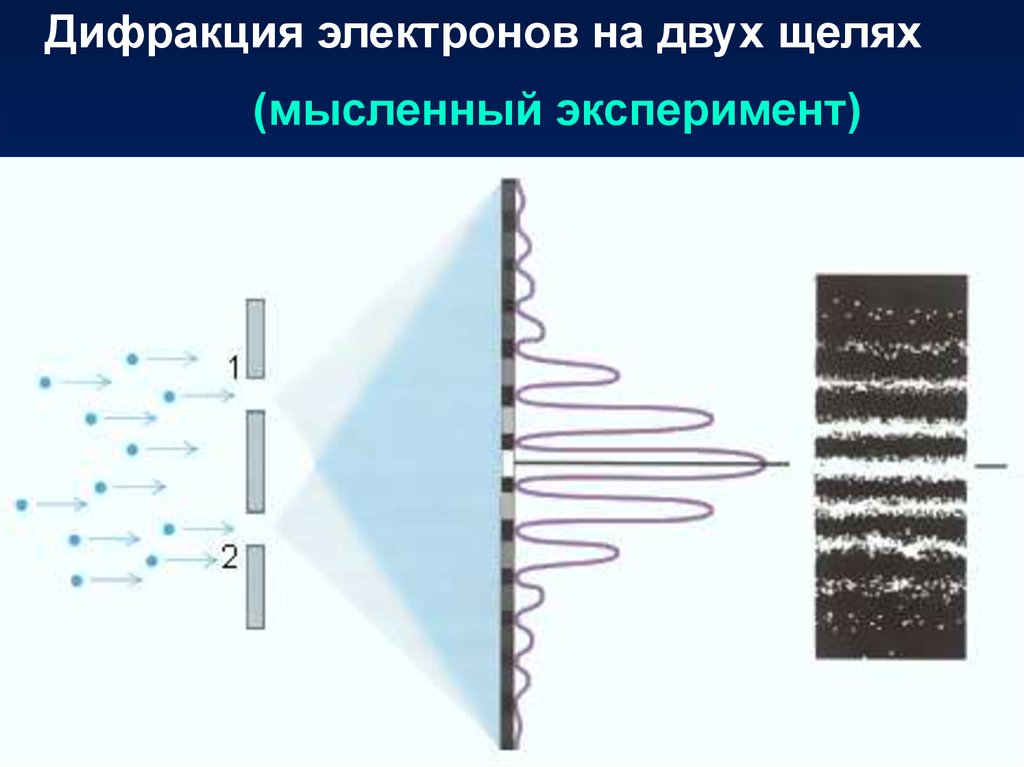
Дифракция электронов на двух щелях
(мысленный эксперимент)

15.

Можно ли экспериментально обнаружить
волновые свойства макрообъекта?
Пуля массой 10 г летит со
скоростью 500 м/с. Определить
длину волны де Бройля для этого
макрообъекта.
34
h
6,63 10 Дж с
34
1,3 10 м.
3
m 10 10 кг 500 м / с
Ответ : ( ? )

16.

Соотношение неопределенностей
Гейзенберг (1927г.): произведение
неопределенностей координаты и
соответствующей ей проекции импульса
не может быть меньше постоянной Планка
x p x ,
y p y ,
z p z .
Квантовое ограничение
применимости классической механики к
микрообъектам.

17.

Дифракция электронов на щели.
График справа – распределение
электронов на фотопластинке

18.

Соотношение неопределенностей
связывает и другие сопряженные
величины – энергию частицы в
возбужденном состоянии и время ее
пребывания в данном состоянии:
E t ,
где
t
E
неопределенность энергии
состояния системы,
промежуток времени существования этого состояния.

19.

Разброс энергии
E / t
возрастает с уменьшением времени
жизни.
Следовательно, неопределенность
частоты E / h увеличивается,
cпектральные линии размыты.

20.

Почему электрон не падает на ядро?
Если электрон приближается к ядру, то
неопределенности в значениях координат
электрона уменьшаются, и увеличиваются
неопределенности в значении импульса
электрона. В системе координат “ядро
атома” средние значения импульса
электрона и его координат равны нулю.

21.

Cледовательно,
p x p x ;
p y p y ;
p z p z ,
x p x / me ;
y p y / me ;
z p z / me .
Кинетическая энергия электрона
увеличиваeтся , электрон
удаляется от ядра.

22.

Уравнение Шредингера
(1926 г.)
- основное уравнение нерелятивистской
квантовой механики.
Временное уравнение Шредингера:
i
U x, y, z , t ,
t
2m
2

23.

где
t
m
i
мнимая единица;
волновая функция;
частная производная волновой
функции по времени;
масса частицы;

24.

2 2 2
x
y
z
2
U x, y, z, t
2
2
оператор
Лапласа;
потенциальная функция
(энергия) частицы в
силовом поле.
Если потенциальная энергия частицы
не зависит от времени, то функции
называются собственными.

25.

В этом случае поведение частицы
описывают стационарным уравнением
Шредингера:
2m
2 W U 0,
где
U
W
полная энергия частицы;
ее потенциальная энергия;
W U Wк кинетическая энергия
частицы.

26.

Волновая
функция должна
удовлетворять условиям:
1) быть конечной, непрерывной и
однозначной;
2) иметь непрерывные производные
,
,
,
;
x y z t

27.

3) функция
должна быть
интегрируема , т.е.
2
2
dxdydz 1
- условие нормировки
функции.