Bi̇lgi̇li̇ arama yöntemleri̇

1.

BİL408 – YAPAY ZEKA
BİLGİLİ ARAMA YÖNTEMLERİ
Dr. Gulshat Muhametjanova
[email protected]

2.

Hatırlatma
• Bilgisiz Arama Yöntemleri
– Genişlik-öncelikli (Breadth-first)
– Eşit-maliyetli (Uniform-cost)
– Derinlik-öncelikli (Depth-first)
– Derinlik-sınırlı (Depth-limited)
– Yinelemeli Derinleşen (Iterative deepening)
– İki Yönlü (Bi-directional)
2

3.

Bilgili Arama
• Bu yöntemler, problem hakkındaki bilgiden
de yararlanarak arama yaparlar
• Bunun için hedefe olan tahmini uzaklık
(maliyet) kullanılır
• Aramayı yönetmek için sezgiseller kullanılır
– Bu tahmini gerçekleyen fonksiyona Sezgisel
(Heuristic) fonksiyonu (h(n)) denilir
3

4.

Bilgili Arama Stratejileri
• En iyi öncelikli (Best-first)
• Aç gözlü (Greedy)
• A*
4

5.

En iyi öncelikli (Best-first) arama
• Genel yaklaşım: Her durum için, o durumun
istenebilirliğini (desirability) tarif edecek bir
tahmin fonksiyonu f(n) kullanılır
• En çok istenen ilerletilmemiş durum ilerletilir
Uygulama:
• Durumları (düğümleri) istenebilirlikleri azalacak
şekilde sırala: Priority Queue
Özel durumlar:
• Aç gözlü arama (greedy search)
• A*arama
5

6.

Aç Gözlü (Greedy) Arama
• Hedef durumuna en yakın olduğu tahmin
edilen/düşünülen durumu ilerletir
• Tahmin fonksiyonu
– f(n) = h(n) = n durumundan hedef duruma kadar
olan, sezgisele göre hesaplanmış masraf
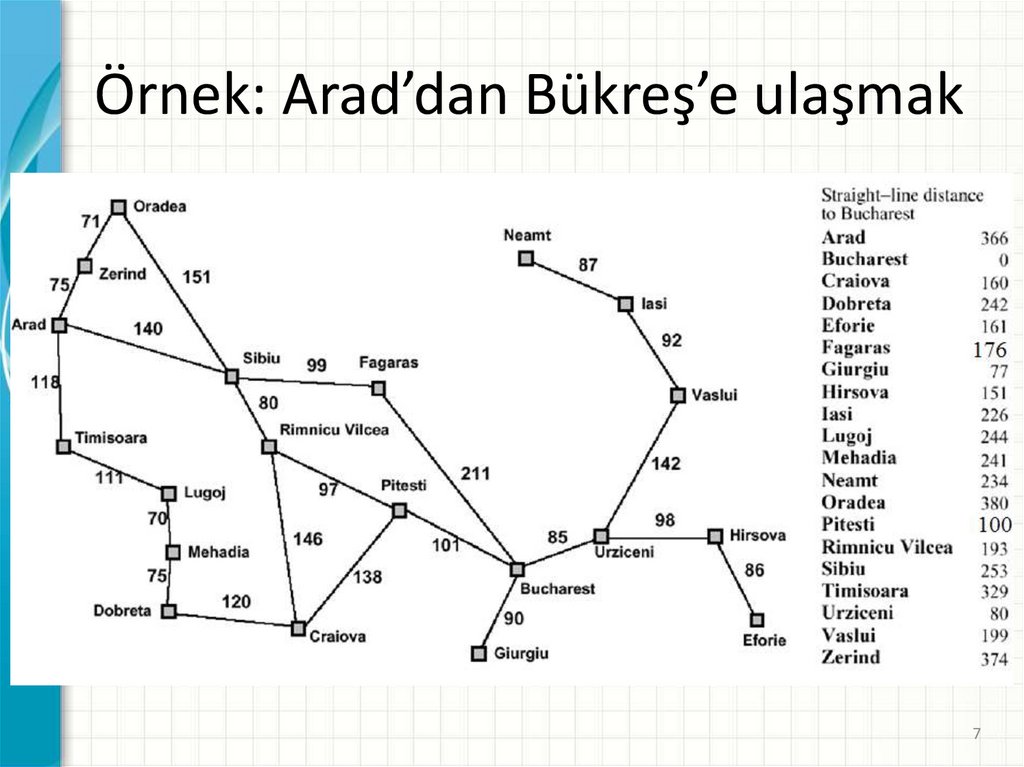
• Örnek: hSLD(n)= n şehrinden İzmir’e kadar
olan kuş uçuşu mesafe
– SLD: Straight Line Distance
– h(n) = 0, n hedef ise
6

7.

Örnek: Arad’dan Bükreş’e ulaşmak
7

8.

Greedy Çözümü
8

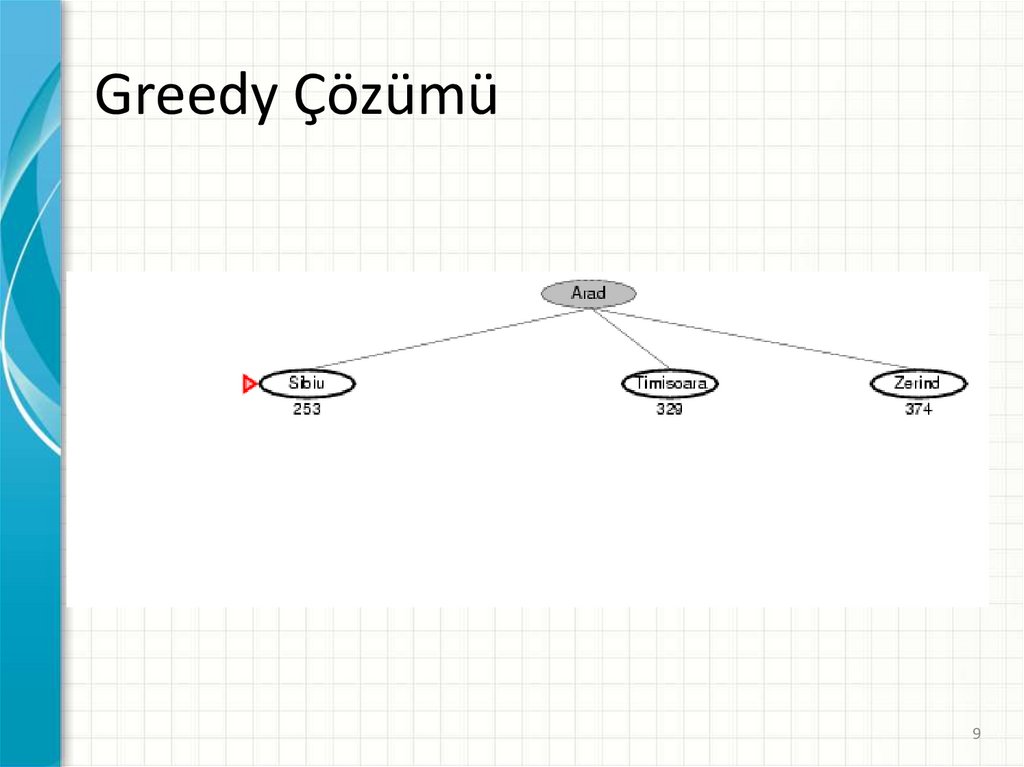
9.

Greedy Çözümü
9

10.

Greedy Çözümü
10

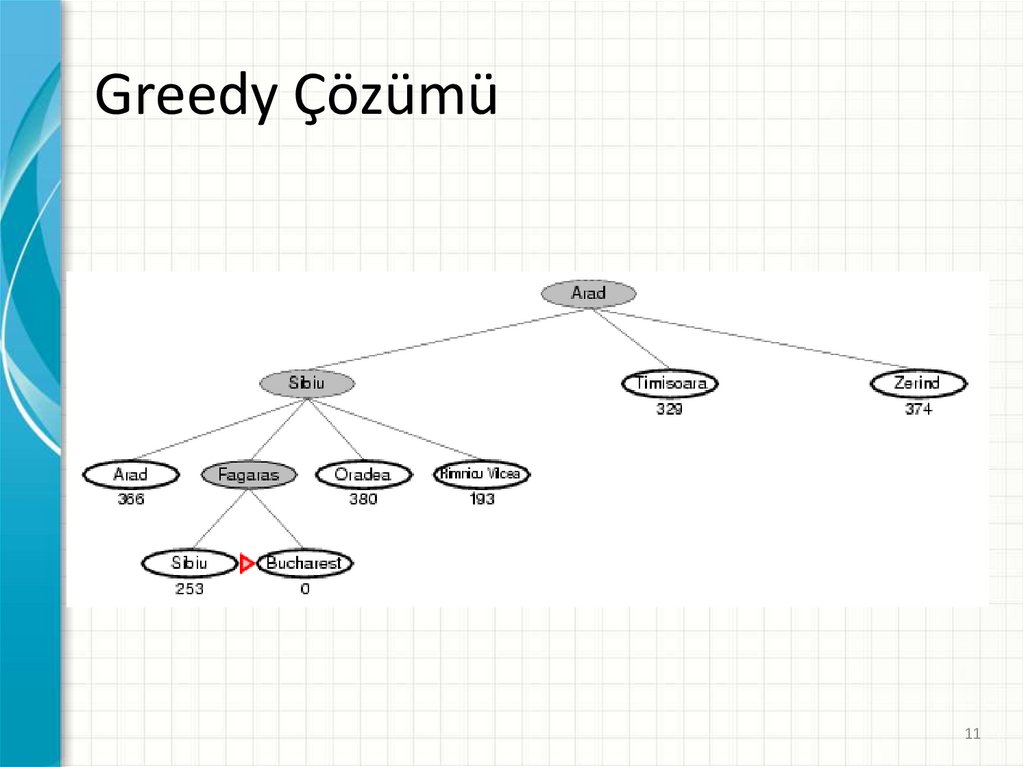
11.

Greedy Çözümü
11

12.

Aç Gözlü: Özellikleri
• Completeness: Hayır
– Döngülerde takılabilir:
– Iasi > Neamt > Iasi > Neamt > …
• Time complexity: O(bm)
– Fakat iyi bir heuristic bu zamanı çok azaltabilir
• Space complexity: O(bm)
– Değerleri karşılaştırmak için bütün düğümleri
bellekte tutar
• Optimality: Hayır
b: dallanma faktörü
m: arama ağacının max derinliği
12

13.

A* Arama
• Ana Fikir: Masraflı olan yolları ilerletmekten
kaçın
• Değerlendirme fonksiyonu: f(n) = g(n) + h(n)
– g(n) : n’e ulaşmak için şimdiye kadarki maliyet
– h(n) : n’den hedefe olan tahmini maliyet
– f(n) : n’den hedefe olan yolun tahmini toplam
maliyeti
• Teorem: A* arama optimaldir
13

14.

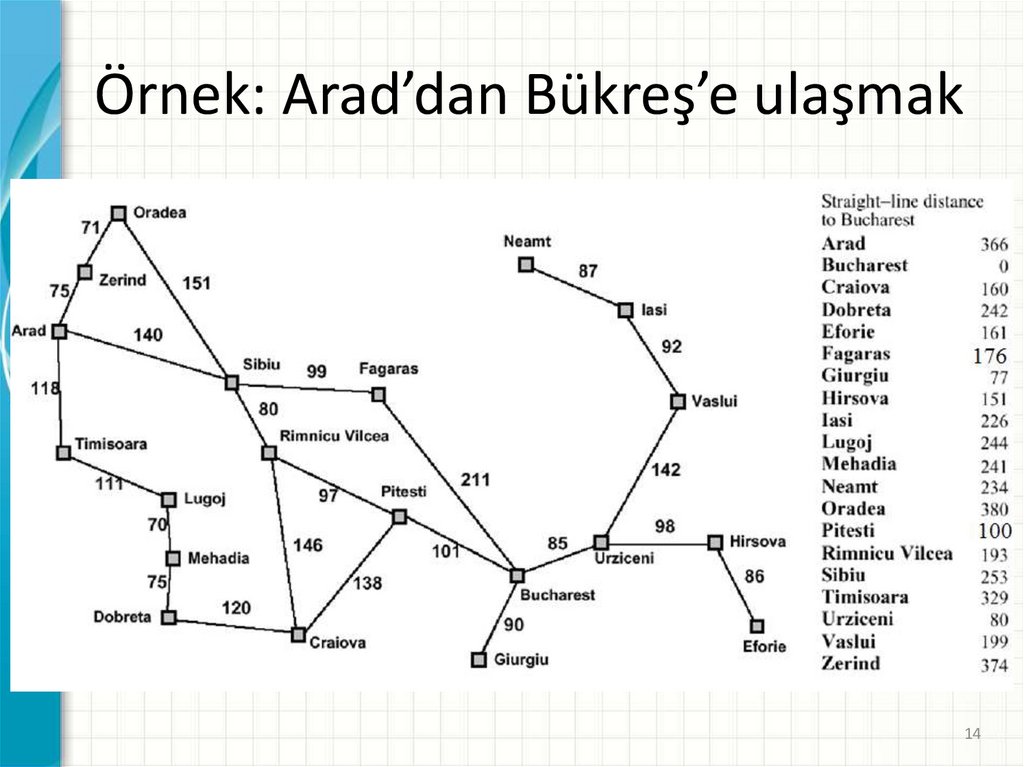
Örnek: Arad’dan Bükreş’e ulaşmak
14

15.

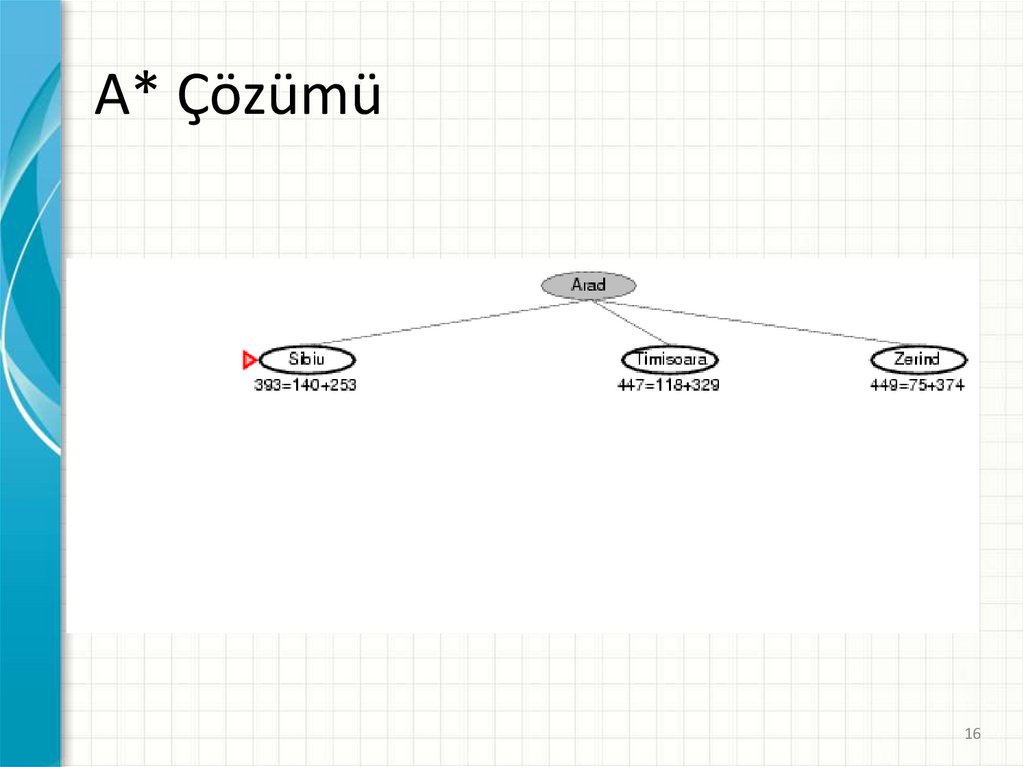
A* Çözümü
15

16.

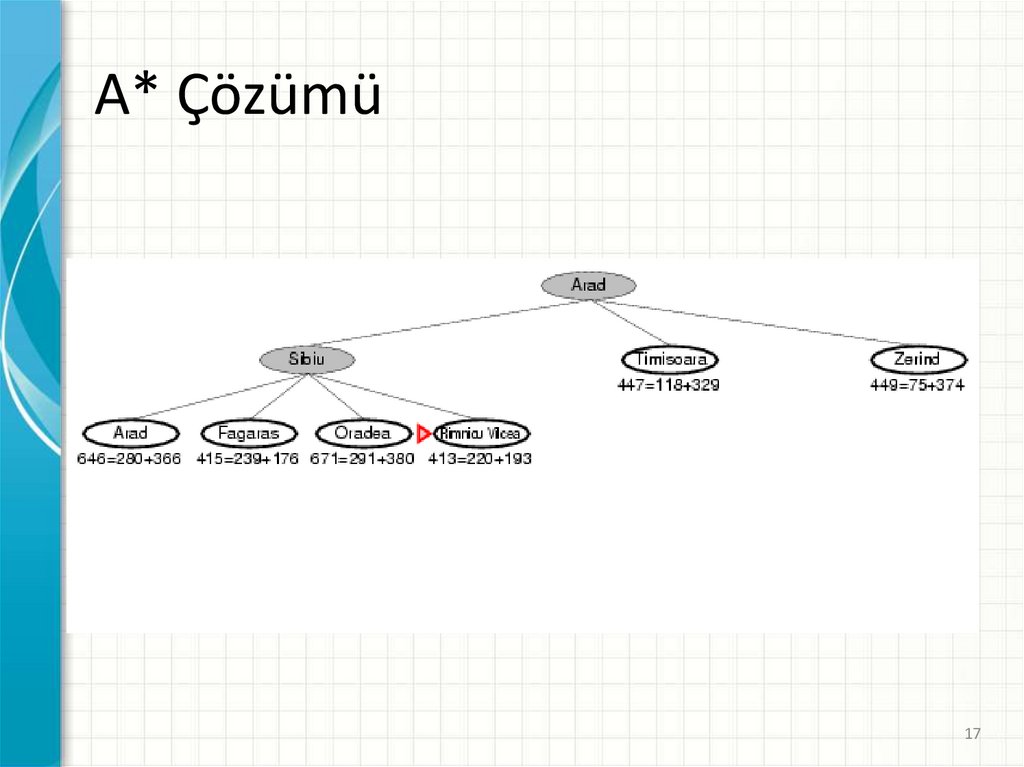
A* Çözümü
16

17.

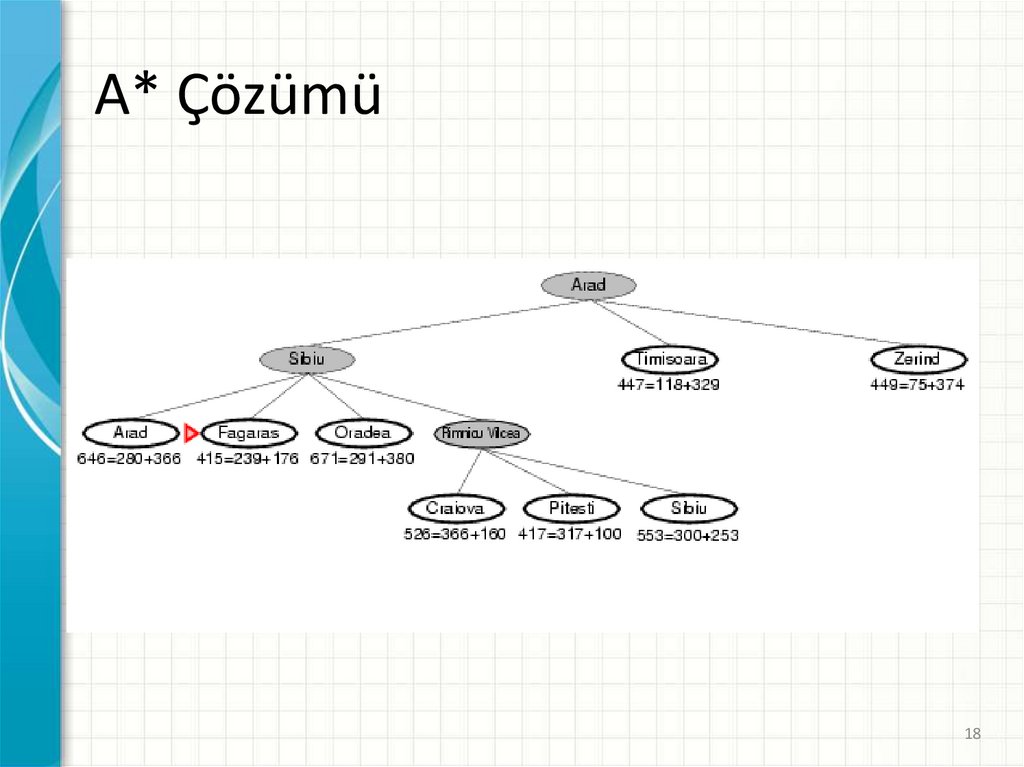
A* Çözümü
17

18.

A* Çözümü
18

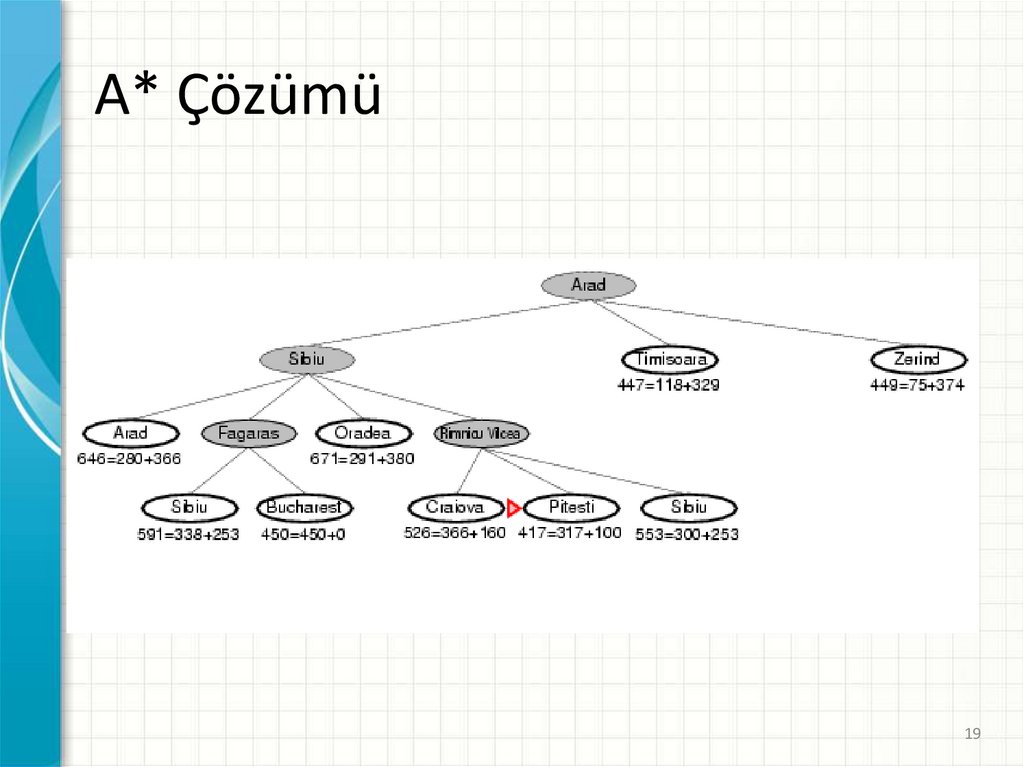
19.

A* Çözümü
19

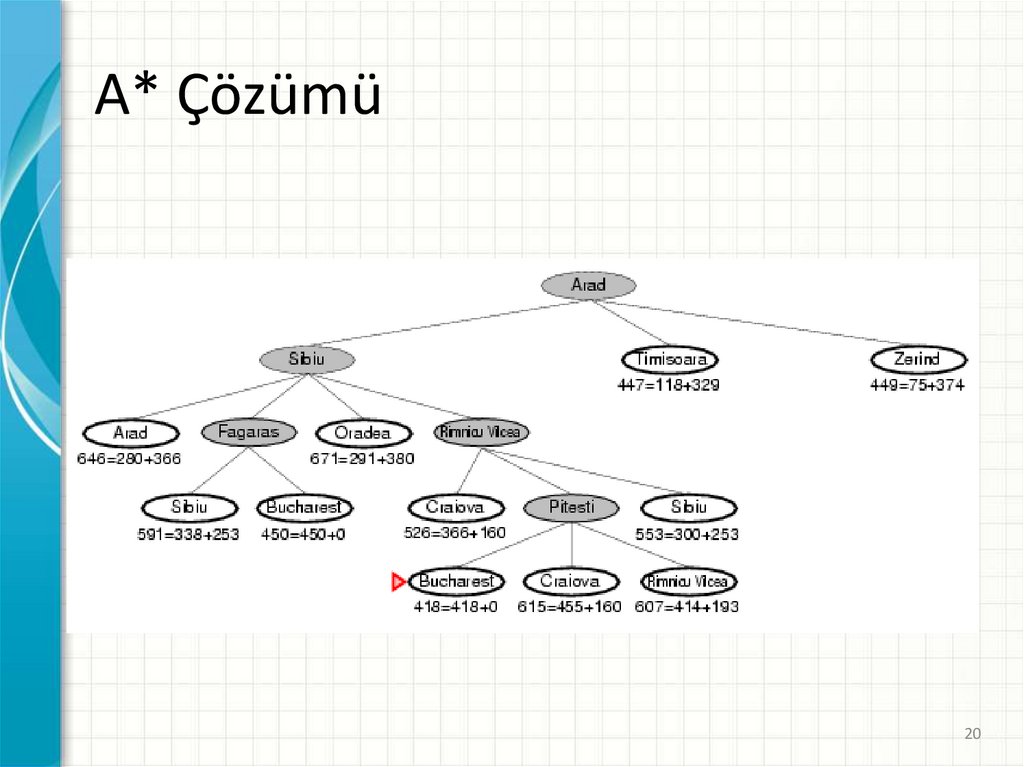
20.

A* Çözümü
20

21.

Örnek-2
4
A
3
5
S
4
4
B
C
5
D
2
E
G
4
3
F
• h(T)= T’ den G’ ye düz yol uzaklığı
A
S
10.4
B
6.7
C 4
11
G
8.9
D
E
6.9
F
3
21

22.

S
3 + 10.4 = 13.4 A
D 4 + 8.9 = 12.9
S
A 13.4
D
9 + 10.4 = 19.4 A
A 13.4
A 13.4
E 6 + 6.9 = 12.9
S
D
19.4 A
11 + 6.7 = 17.7 B
E
F 10 + 3.0 = 13.0
S
19.4 A
D
17.7 B
E
DUR!
F
G 13 + 0.0 = 13.0
22

23.

A* Özellikleri
• Completeness: Evet
– Döngülere girmediği için
• Time complexity: Kullanılan sezgisele göre
değişebilir
– En kötü durum (worst case): Çözüm yolunun
uzunluğunda eksponansiyel
• Space complexity: O(bm)
– Bütün düğümleri bellekte tutar
• Optimality: Evet
b: dallanma faktörü
m: arama ağacının max derinliği
23

24.

Optimallik
IF for tüm T: h(T) ile hedef düğüme kalan maliyetin altında paha
biçilmişse (UNDERestimate)
THEN A* optimal dir.
• hSLD(n): her zaman gerçek uzaklıktan küçük olduğundan
kabul edilebilir sezgiseldir
Değerinin
altında paha
biçilen kalan
maliyeti
içerir
A 13.4
S
19.4 A
D
17.7 B
Gerçek kalan maliyetle
bu yol en az 13.4 olmalıdır
E
F
G 13
G
24

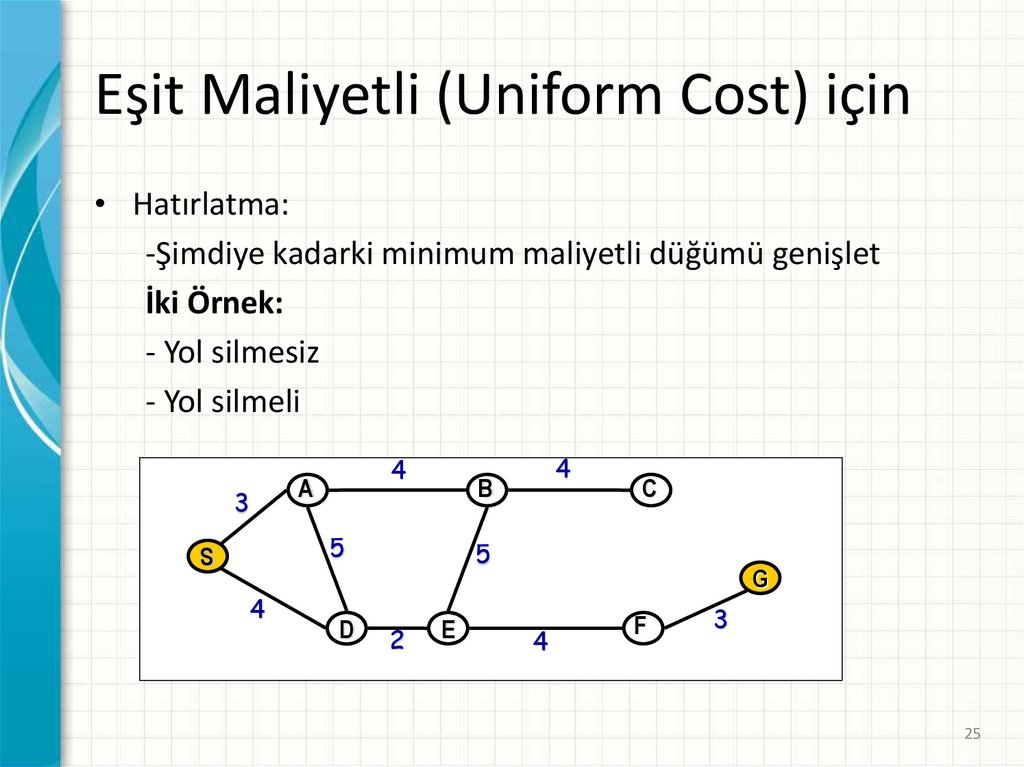
25.

Eşit Maliyetli (Uniform Cost) için
• Hatırlatma:
-Şimdiye kadarki minimum maliyetli düğümü genişlet
İki Örnek:
- Yol silmesiz
- Yol silmeli
4
A
3
5
S
4
D
4
B
C
5
2
E
G
4
F
3
25

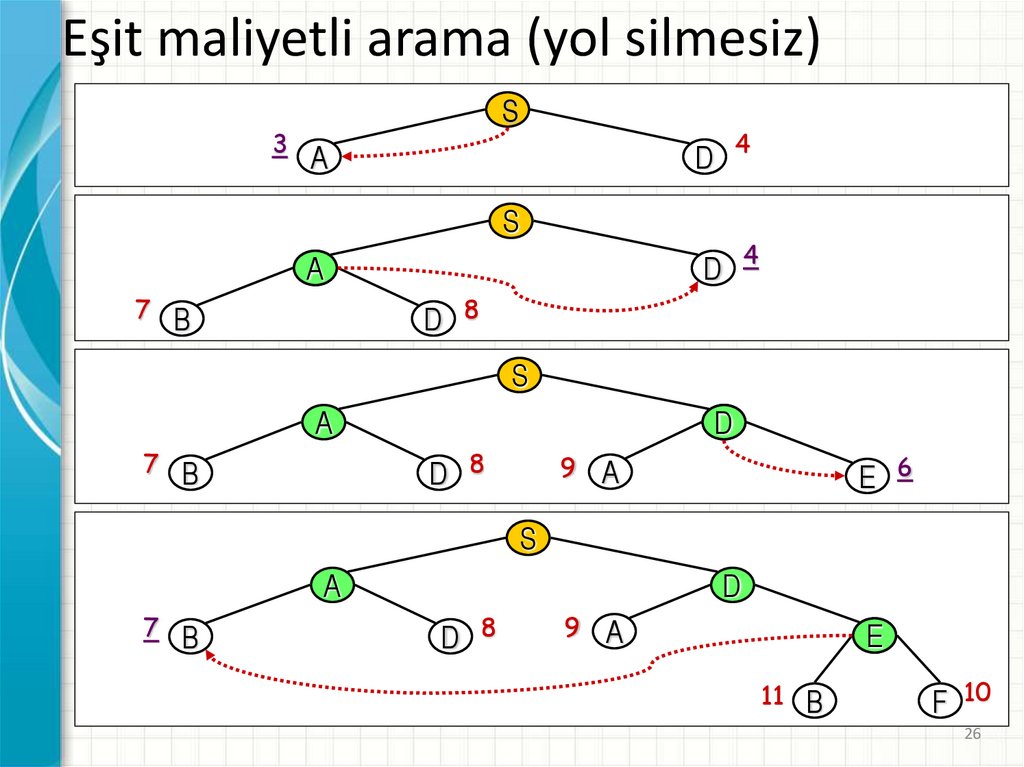
26.

Eşit maliyetli arama (yol silmesiz)
3
S
A
4
D
S
A
7
4
D
D 8
B
S
A
7
D
D 8
B
9
E 6
A
S
A
7
B
D
D 8
9
A
E
11
B
F 10
26

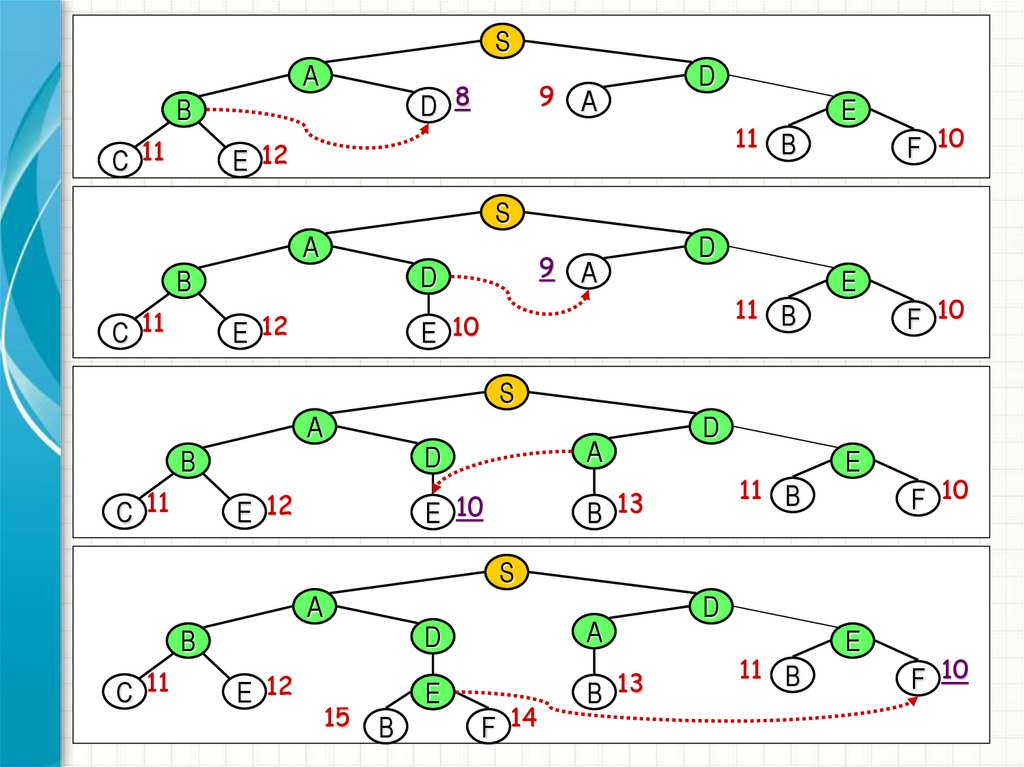
27.

S
A
B
C 11
9
D 8
A
D
11 B
E 12
E
F 10
S
A
D
B
C 11
9
E 12
A
D
11 B
E 10
E
F 10
S
A
B
C 11
E 12
D
A
E 10
B 13
D
11 B
E
F 10
S
A
B
C 11
E 12
15
B
D
A
E
B 13
F 14
D
11 B
E
F 10
27

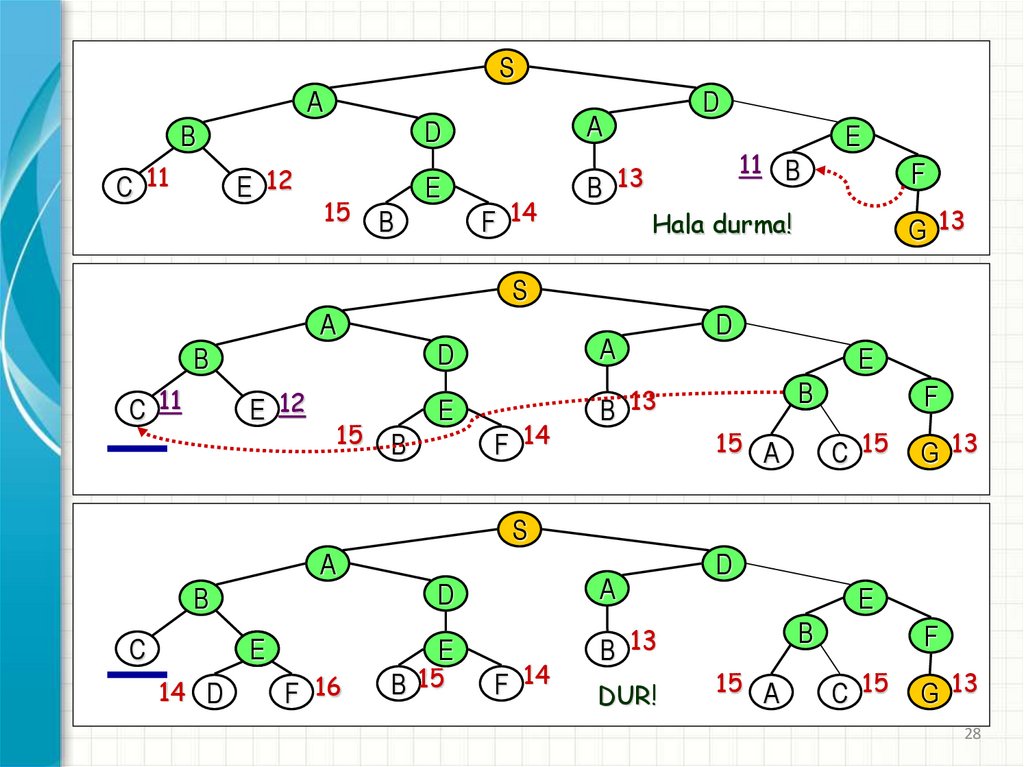
28.

S
A
B
C 11
E 12
15
D
A
E
B 13
B
F 14
D
11 B
E
F
G 13
Hala durma!
S
A
B
C 11
E 12
15
D
A
E
B 13
B
F 14
D
E
B
15 A
F
C 15
G 13
S
A
B
C
E
14 D
F 16
D
A
E
B 13
B 15
F 14
DUR!
D
E
B
15 A
F
C 15
G 13
28

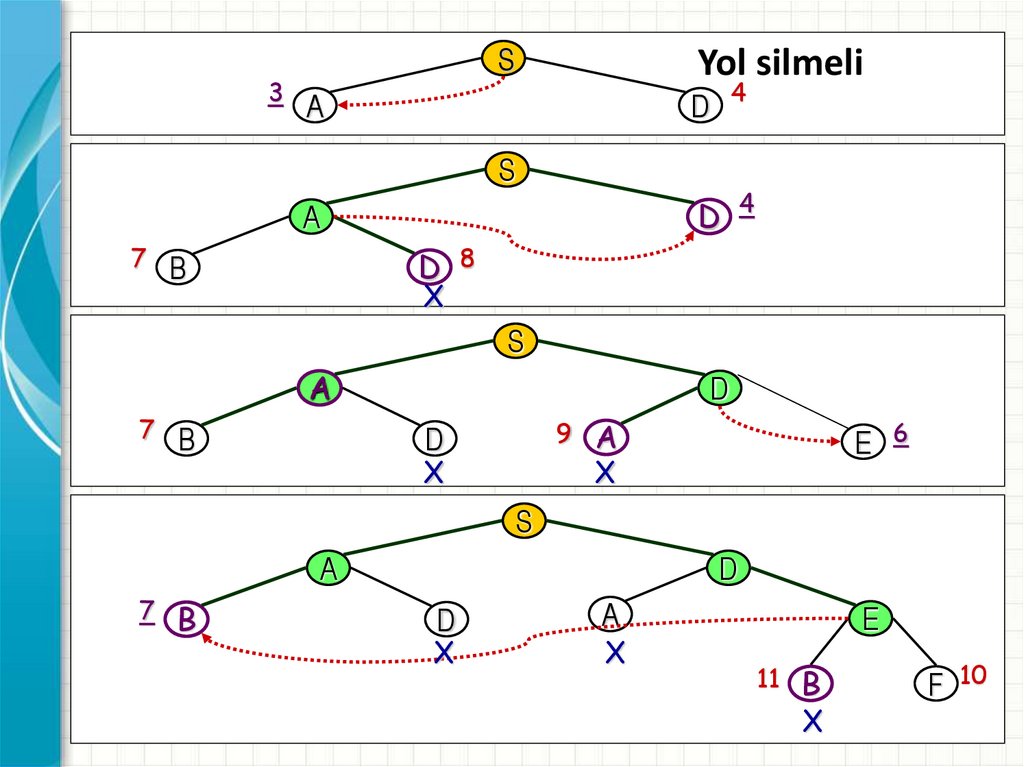
29.

3
S
Yol silmeli
A
S
D 4
A
7
4
D
D 8
B
X
S
A
7
B
D
9
D
X
E 6
A
X
S
A
7
B
D
D
X
A
X
E
11
B
X
F 10
29

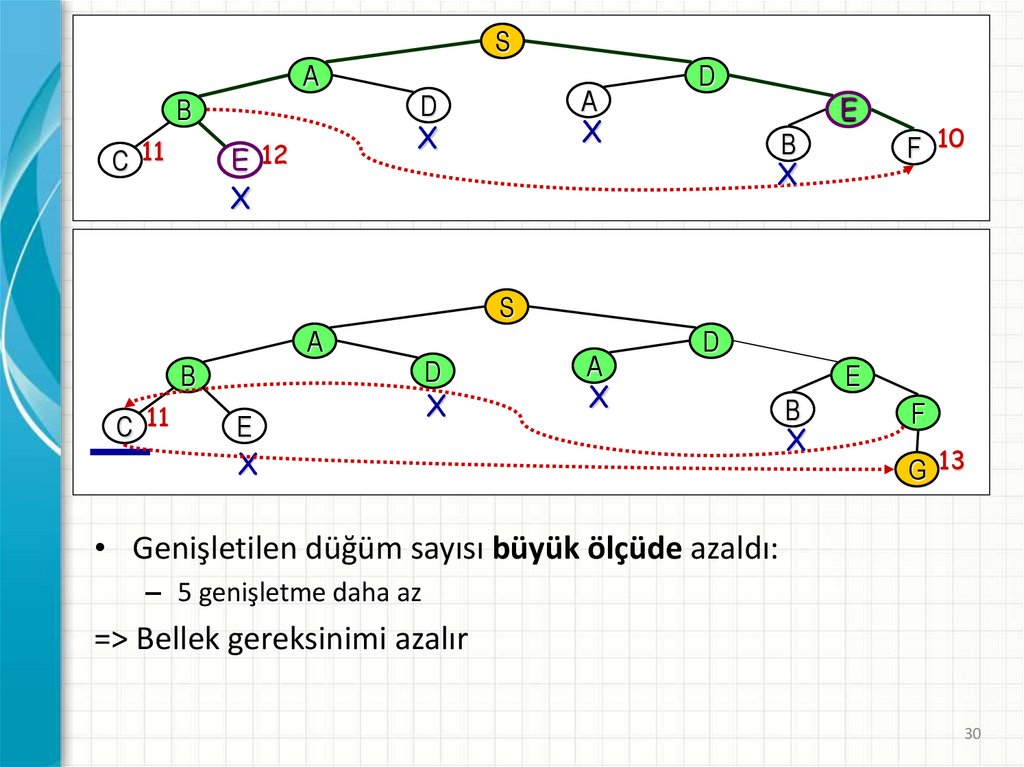
30.

S
A
B
C 11
E 12
A
X
D
X
D
E
B
X
X
F 10
S
A
B
C 11
E
X
D
X
A
X
D
E
B
X
F
G 13
• Genişletilen düğüm sayısı büyük ölçüde azaldı:
– 5 genişletme daha az
=> Bellek gereksinimi azalır
30

31.

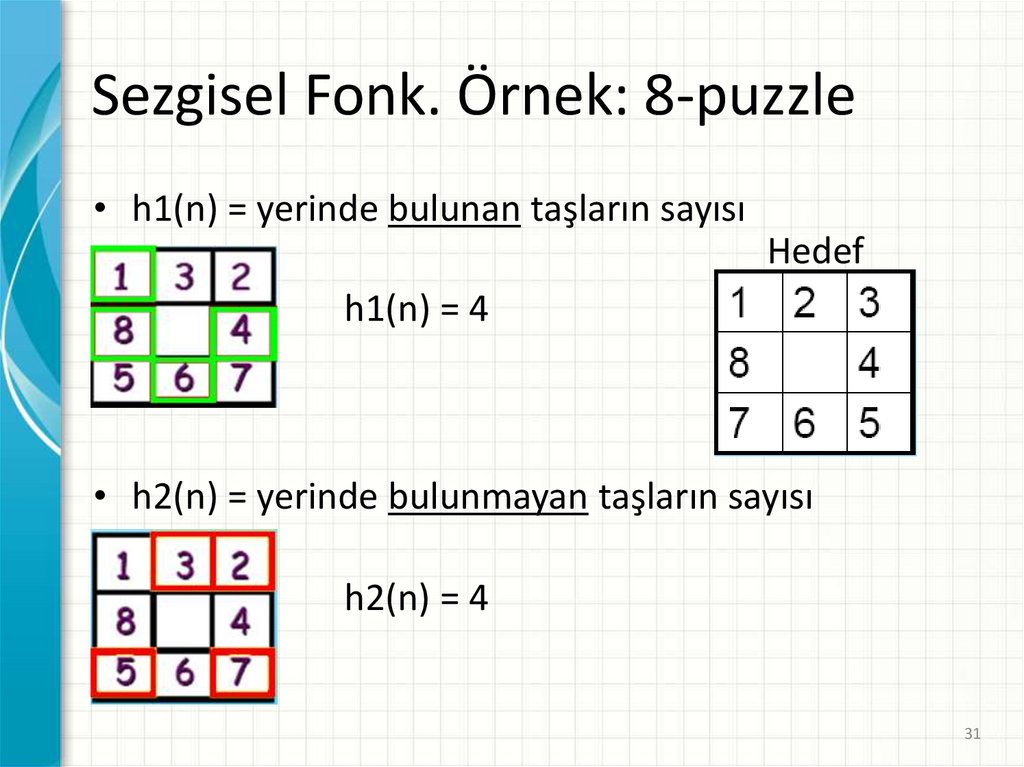
Sezgisel Fonk. Örnek: 8-puzzle
• h1(n) = yerinde bulunan taşların sayısı
Hedef
h1(n) = 4
• h2(n) = yerinde bulunmayan taşların sayısı
h2(n) = 4
31

32.

Sezgisel Fonk. Örnek: 8-puzzle
• h3(n) = taşların hedefteki yerlerine uzaklıkları
toplamı (yatay ve dikey hane toplamları)
• Bu uzaklıklara Manhattan uzaklığı da denir
h3(n) = 1 + 1 + 2 + 2 = 6
32

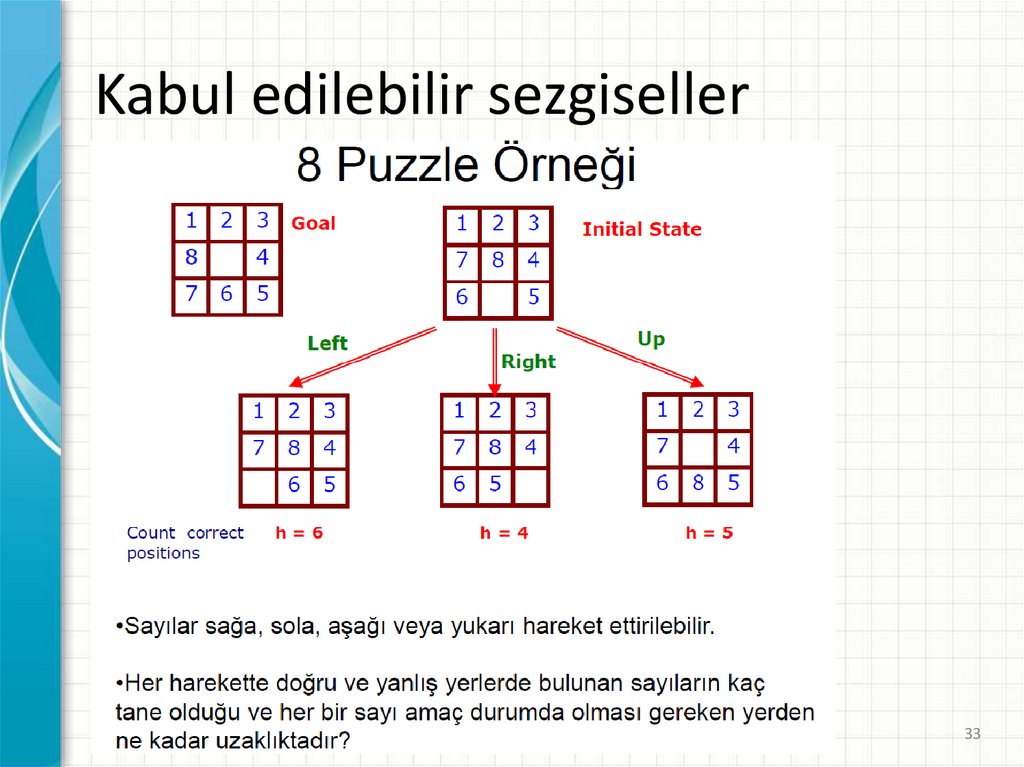
33.

Kabul edilebilir sezgiseller
33

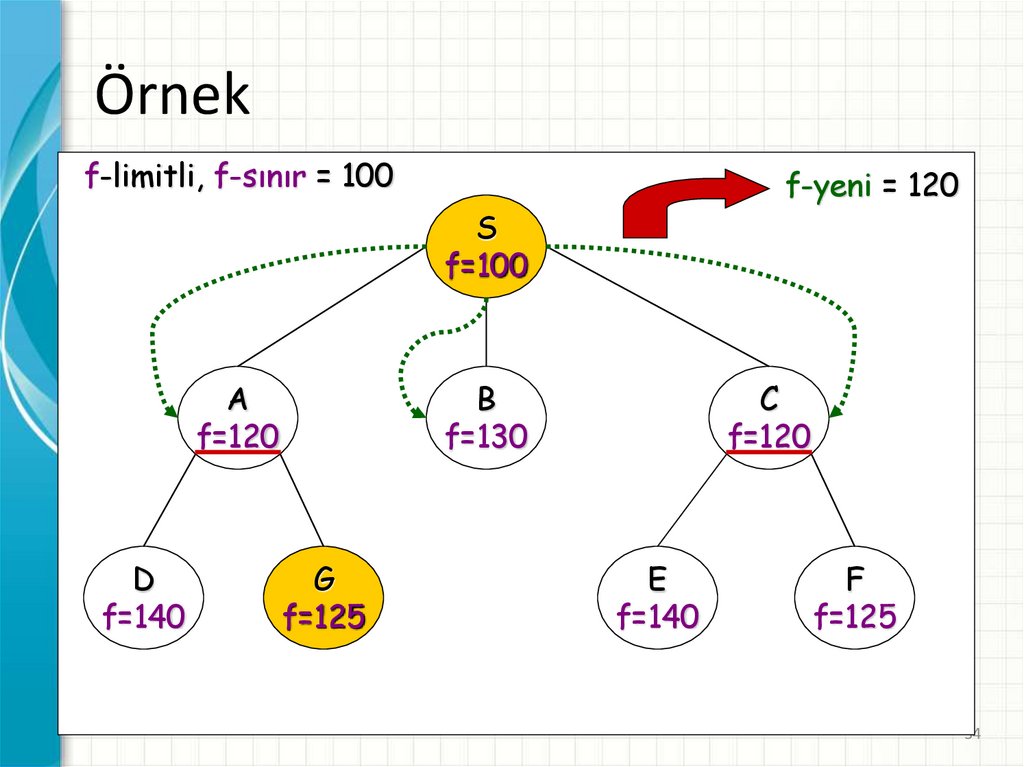
34.

Örnek
f-limitli, f-sınır = 100
f-yeni = 120
S
f=100
A
f=120
D
f=140
B
f=130
G
f=125
C
f=120
E
f=140
F
f=125
34

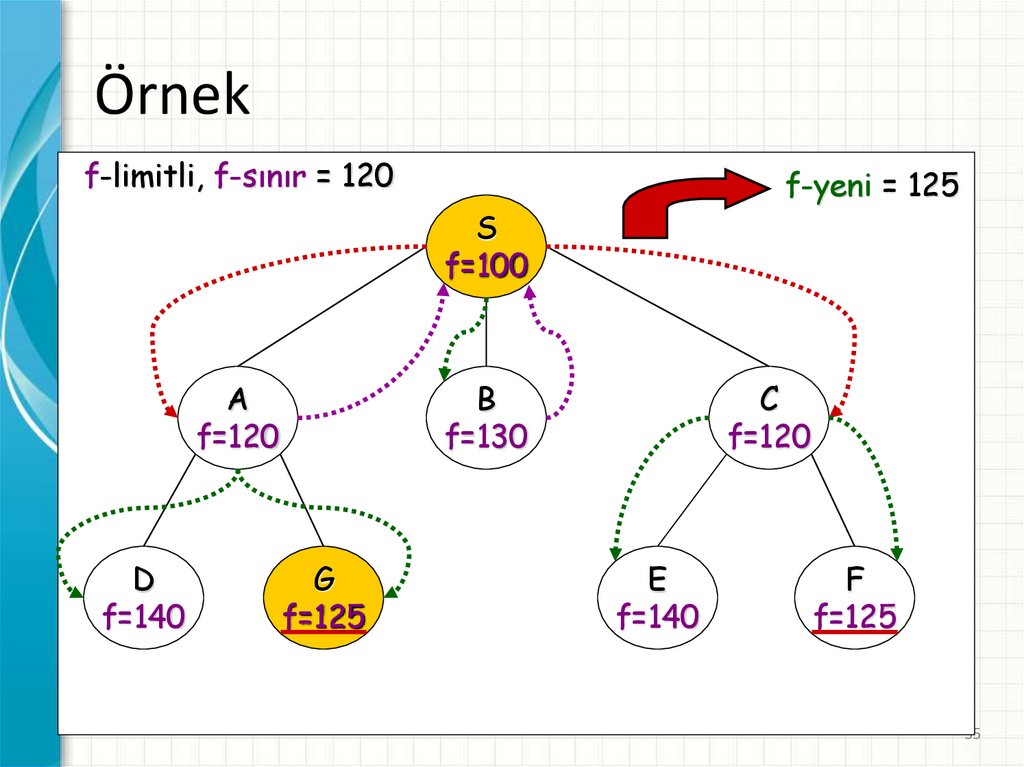
35.

Örnek
f-limitli, f-sınır = 120
f-yeni = 125
S
f=100
A
f=120
D
f=140
B
f=130
G
f=125
C
f=120
E
f=140
F
f=125
35

36.

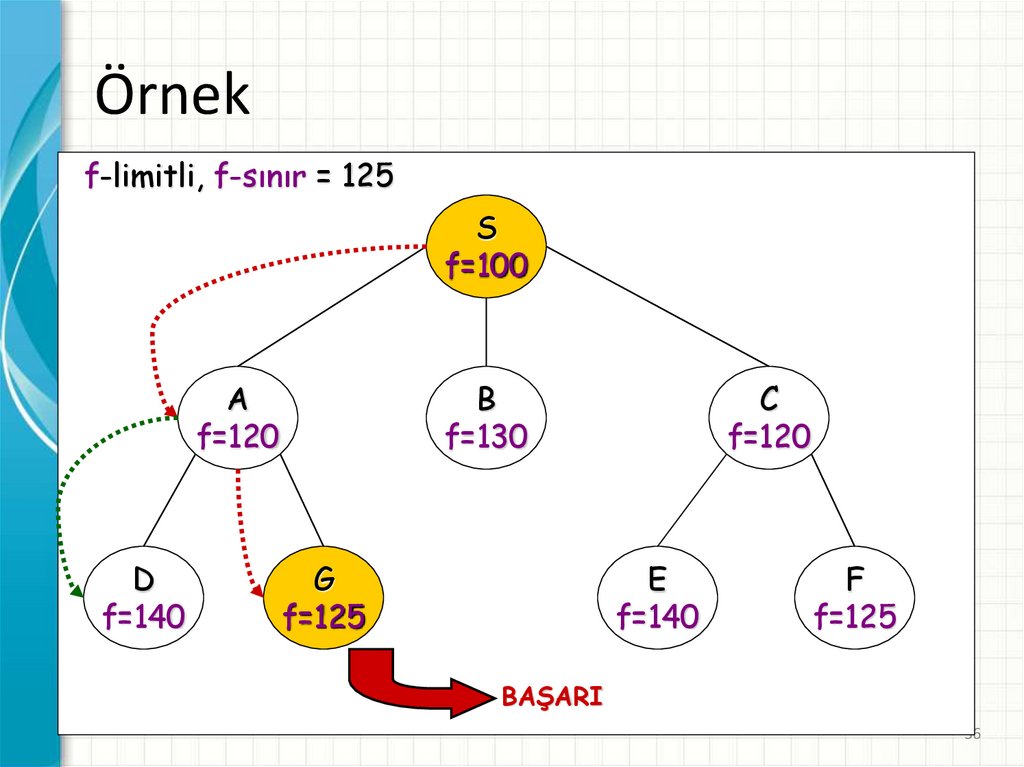
Örnek
f-limitli, f-sınır = 125
S
f=100
A
f=120
D
f=140
B
f=130
G
f=125
C
f=120
E
f=140
F
f=125
BAŞARI
36

37.

SONUÇ: Bilgisiz ve Bilgili Arama
• Bilgisiz arama algoritmaları, düğümlerin amaca
uzaklığı hakkında bir bilgiye sahip değildirler. Eğer
belirli sayıda düğüm varsa, uygun çözüm bulunabilir
• Bilgili arama yaklaşımlarında, amaca olan tahmini
uzaklık kullanılır. Amaca yakın olan düğümler ilk
önce açılır. Çözümün bulunması garanti değildir. Bu
yöntemlerin başarılı olmasında doğru
değerlendirme fonksiyonunun seçilmesi önemli rol
oynar
37

38.

SORULAR?
38