Перпендикулярность прямых и плоскостей

1. Перпендикулярность прямых и плоскостей

2.

Определение. Две прямые называются
перпендикулярными, если они пересекаются
под прямым углом.
Определение. Прямая, пересекающая
плоскость, называется перпендикулярной к
этой плоскости, если она .перпендикулярна
любой прямой, которая лежит в данной
плоскости.

3.

Перпендикулярные прямые в пространстве.
Лемма.
Если одна из двух параллельных
прямых перпендикулярна
к третьей прямой, то и другая прямая
перпендикулярна к этой прямой.

4.

Параллельные прямые, перпендикулярные к плоскости
Теорема.
Если одна из двух параллельных
прямых перпендикулярна
к плоскости, то и другая прямая
перпендикулярна к этой плоскости.
Обратная теорема.
Если две прямые перпендикулярны к
плоскости, то они параллельны

5.

1)
2)
3)

6.

Признак перпендикулярности прямой и плоскости.
Теорема.
Если прямая перпендикулярна к двум
пересекающимся прямым, лежащим в
плоскости, то она перпендикулярна к
этой плоскости.

7.

Признак перпендикулярности прямой и плоскости.
Теорема.
Через любую точку пространства проходит
Прямая , перпендикулярная к данной
плоскости, и притом только одна.

8.

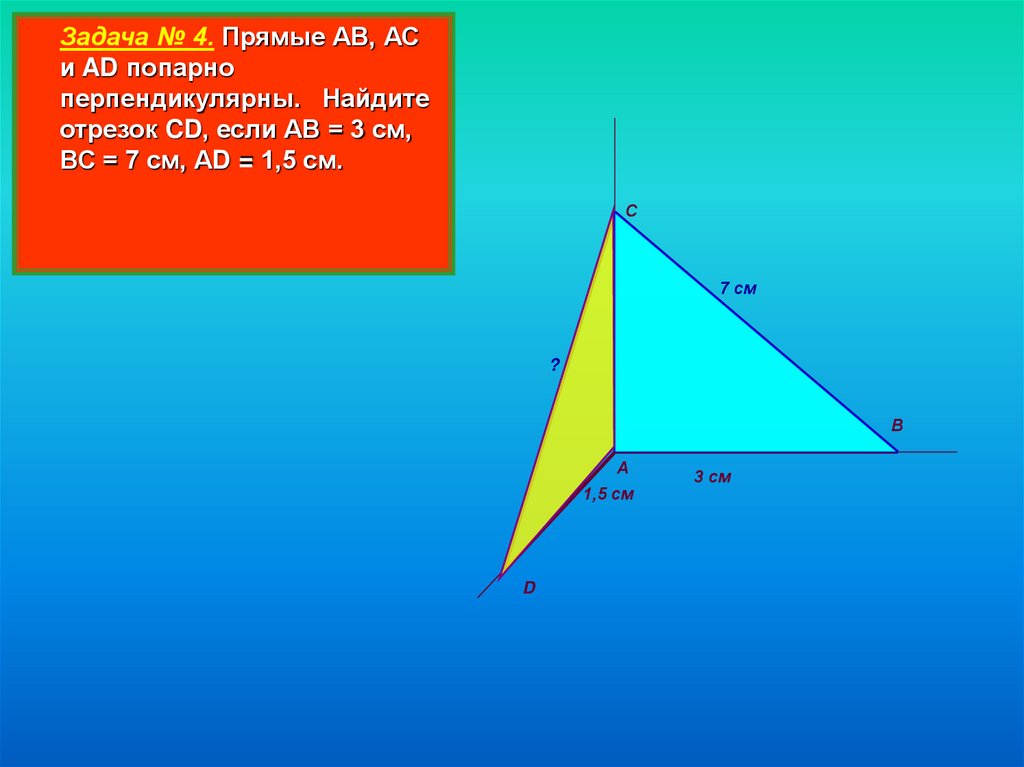
Задача № 4. Прямые АВ, АС
и AD попарно
перпендикулярны. Найдите
отрезок CD, если АВ = 3 см,
ВС = 7 см, АD = 1,5 см.
С
7 см
?
В
А
1,5 см
D
3 см

9.

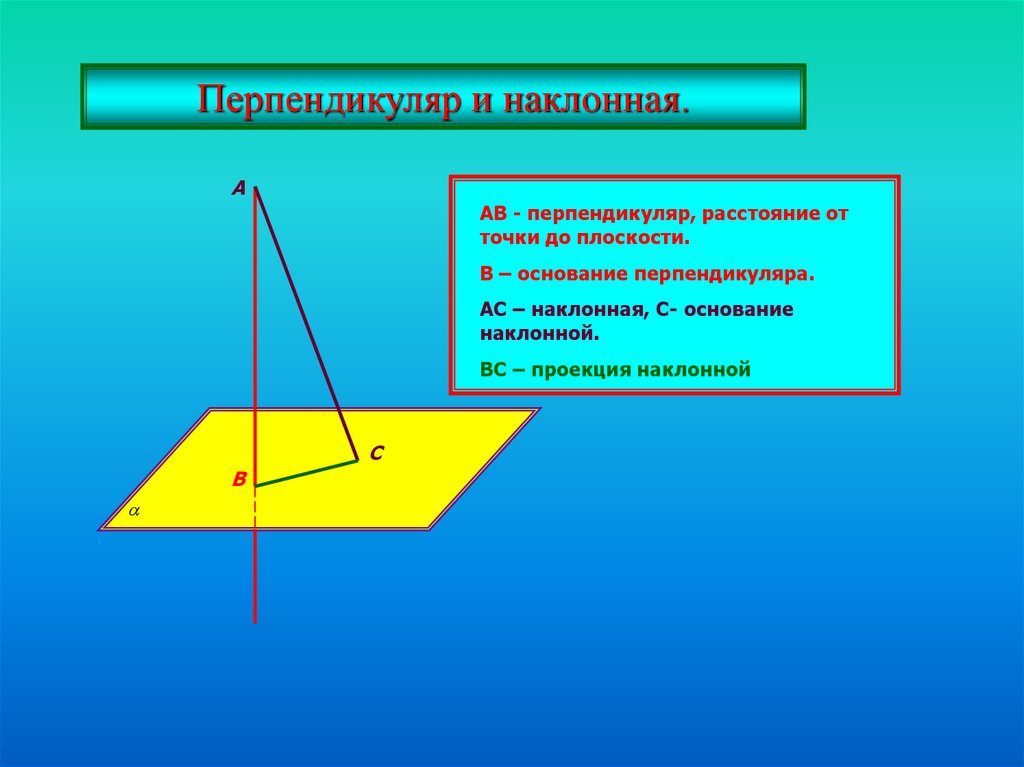
Перпендикуляр и наклонная.
А
АВ - перпендикуляр, расстояние от
точки до плоскости.
В – основание перпендикуляра.
АС – наклонная, С- основание
наклонной.
ВС – проекция наклонной
С
В

10.

А
Задача 6 Из точки к
плоскости проведены две
наклонные. Найдите длины
наклонных, если наклонные
относятся как 1:2, а проекции
наклонных равны 1 см и 7 см.
О
С
В

11.

12.

Двугранным углом называется фигура, образованная
прямой
a и двумя полуплоскостями с общей границей
a, не принадлежащими одной плоскости.
Прямая a – ребро двугранного угла
a
Две полуплоскости – грани двугранного угла

13.

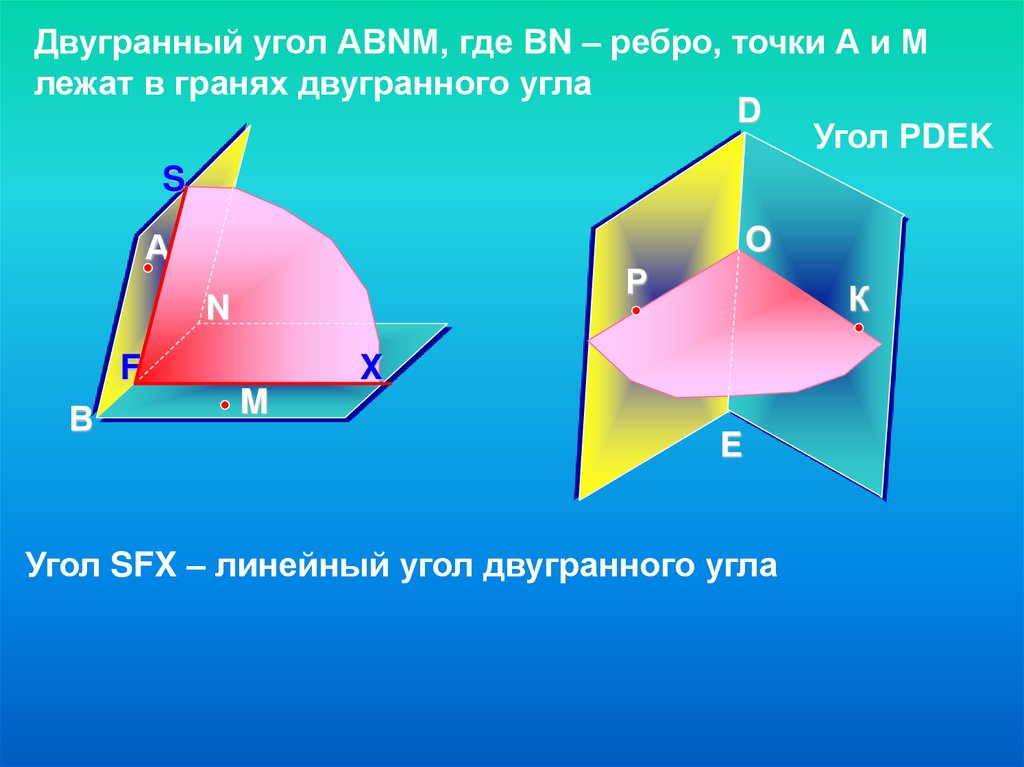
Двугранный угол АВNМ, где ВN – ребро, точки А и М
лежат в гранях двугранного угла
D
Угол РDEK
S
O
А
Р
N
F
В
К
X
M
E
Угол SFX – линейный угол двугранного угла

14.

Все линейные углы двугранного угла равны друг другу.
O
А
В
O
А1
1
В1

15.

Двугранный угол может быть прямым, острым,
тупым

16.

Плоскости и взаимно перпендикулярны
пересекаются по прямой с. Докажите, что любая прямая
плоскости , перпендикулярная к прямой с,
перпендикулярна к плоскости .
A
c
C
B

17.

Задача № 5. Прямые АВ, АС
и AD попарно
перпендикулярны. Найдите
отрезок CD, если ВD = 9 см,
ВС = 16 см, АD = 5 см.
С
?
В
А
D

18.

Задача 7 Из точек А и
В, лежащих в двух
перпендикулярных
плоскостях, опущены
перпендикуляры АС и
ВD на прямую
пересечения
плоскостей. Найдите
длину отрезка АВ,
если:
АС = 4 м, ВD =
12 м, СD = 6 м.
• А
?
4м
900
D
6м
С
900
В
12
м