Перпендикулярность прямых и плоскостей. Повторение

1.

2.

Повторение
Определение. Прямая называется перпендикулярной к
плоскости, если она перпендикулярна к любой прямой,
лежащей в этой плоскости.
a
S
F
A
a
N
D
H
a AS , a AF , a FS , a ND, a DH , a HN

3.

Повторение
Признак перпендикулярности прямой и плоскости.
Если прямая перпендикулярна к двум
пересекающимся прямым, лежащим в плоскости, то
она перпендикулярна к этой плоскости.
a
p
p , a p,
q , a q,
a

4.

Планиметрия
Стереометрия
А
А
а
М
Н
М
Н
Отрезок АН – перпендикуляр
Точка Н – основание перпендикуляра
Отрезок АМ – наклонная
Точка М – основание наклонной
Отрезок МН – проекция
наклонной на прямую а
Отрезок МН – проекция
наклонной на плоскость

5.

Планиметрия
Стереометрия
А
А
а
М
Н
Н
М
Из всех расстояний от точки А
до различных точек прямой
а
плоскости
наименьшим является длина
перпендикуляра.
Расстояние от точки до
Расстояние от точки до
прямой – длина
плоскости – длина
перпендикуляра
перпендикуляра

6.

Если две плоскости параллельны, то все точки одной
плоскости равноудалены от другой плоскости.
II
Расстояние от произвольной точки одной из параллельных
плоскостей до другой плоскости называется
расстоянием между параллельными плоскостями.

7.

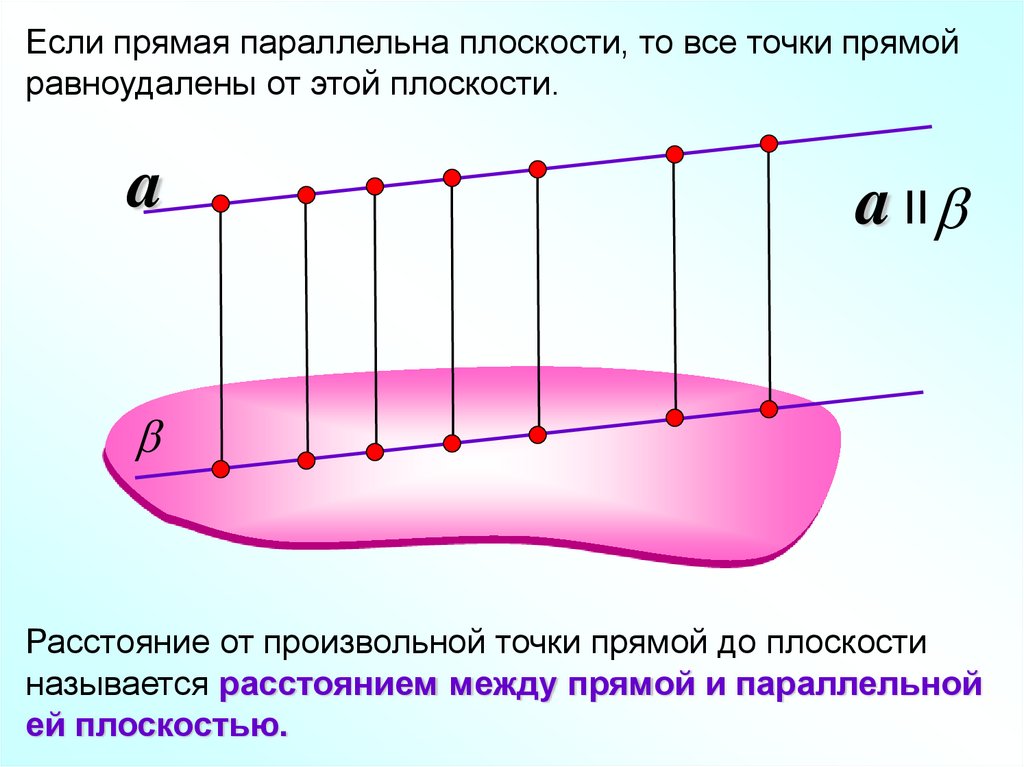
Если прямая параллельна плоскости, то все точки прямой
равноудалены от этой плоскости.
a
a II
Расстояние от произвольной точки прямой до плоскости
называется расстоянием между прямой и параллельной
ей плоскостью.

8.

Если две прямые скрещиваются, то через каждую из них
проходит плоскость, параллельная другой прямой, и притом
только одна.
a
a b
a II
b
Расстояние между одной из скрещивающихся прямых и
плоскостью, проходящей через другую прямую параллельно
первой, называется расстоянием между
скрещивающимися прямыми.

9.

Расстояние
Отрезок, имеющий
между одной
концы
изна
скрещивающихся
двух скрещивающихся
прямых и
плоскостью,
прямых и перпендикулярный
проходящей черезкдругую
этим прямым,
прямую называется
параллельно
первой,
их общим
называется
перпендикуляром.
расстоянием между
скрещивающимися
На рисунке АВ – общий
прямыми.
перпендикуляр.
В
А

10.

Теорема о трех перпендикулярах.
Прямая, проведенная в плоскости через основание
наклонной перпендикулярно к ее проекции на эту
плоскость, перпендикулярна и к самой наклонной.
А
П-Р
Н
Н-я
П-я
М
a

11.

Обратная теорема.
Прямая, проведенная в плоскости через основание
наклонной перпендикулярно к ней,
перпендикулярна и к ее проекции.
А
П-Р
Н
Н-я
П-я
М
a

12.

Через вершину А прямоугольника АВСD проведена прямая
АК, перпендикулярная к плоскости прямоугольника. Известно,
что КD = 6 см, КВ = 7 см, КС = 9 см. Найдите:
КА – искомое расстояние
а) расстояние от точки К до плоскости прямоугольника АВСD;
б) расстояние между прямыми АК и СD. АD – общий перпендикуляр
АD – искомое расстояние
№150.
K
Найдем другие прямые углы…
СD AD
6
D
9
П-я 1
С
П-я 1
П-Р
?
А
BC BA
7
П-я 2
В
TTП
CD DK
Н-я 1
TTП
BC BK
Н-я 2

13.

Углом между прямой и плоскостью, пересекающей эту
прямую и не перпендикулярной к ней, называется угол
между прямой и ее проекцией на плоскость.
М
Н-я
А
П-Р
П-я
Н

14.

Найти угол между наклонными и плоскостью
(описать алгоритм построения).
М
М
H
F
H
FМ
П-Р
F
А
R
Н
К
FH

15.

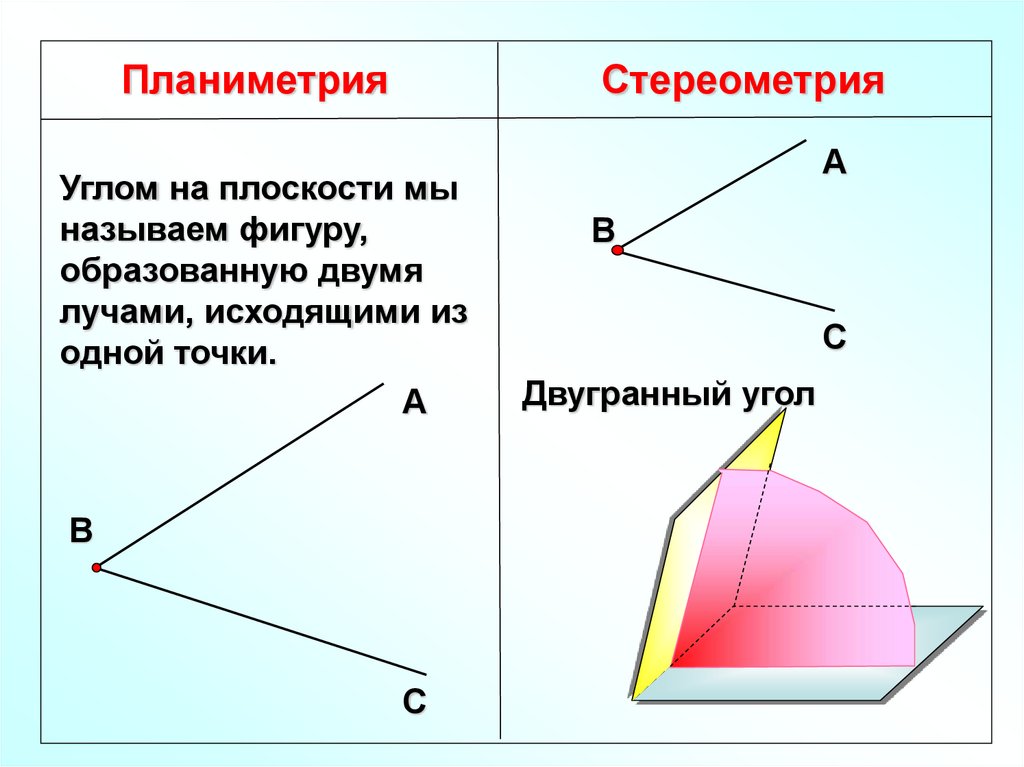
Планиметрия
Стереометрия
Углом на плоскости мы
называем фигуру,
образованную двумя
лучами, исходящими из
одной точки.
А
В
С
А
В
С
Двугранный угол

16.

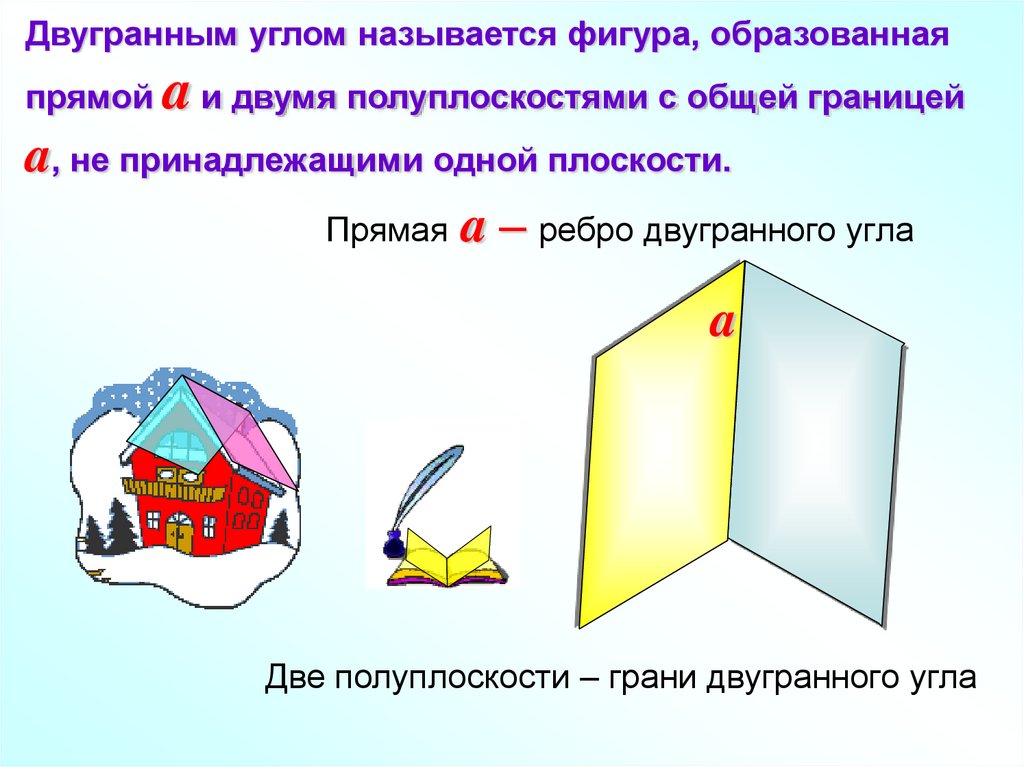
Двугранным углом называется фигура, образованная
прямой
a и двумя полуплоскостями с общей границей
a, не принадлежащими одной плоскости.
Прямая a – ребро двугранного угла
a
Две полуплоскости – грани двугранного угла

17.

Алгоритм построения линейного угла.
Угол РОК – линейный угол двугранного угла РDEК.
D
Градусной мерой двугранного
угла называется градусная мера
его линейного угла.
O
Р
К
E
Плоскость линейного угла ( РОК ) DE

18.

Все линейные углы двугранного угла равны друг другу.
Лучи ОА и О1А1 – сонаправлены
Лучи ОВ и О1В1 – сонаправлены
O
А
В
Углы АОВ и А1О1В1 равны,
как углы с сонаправленными
сторонами
O
А1
1
В1

19.

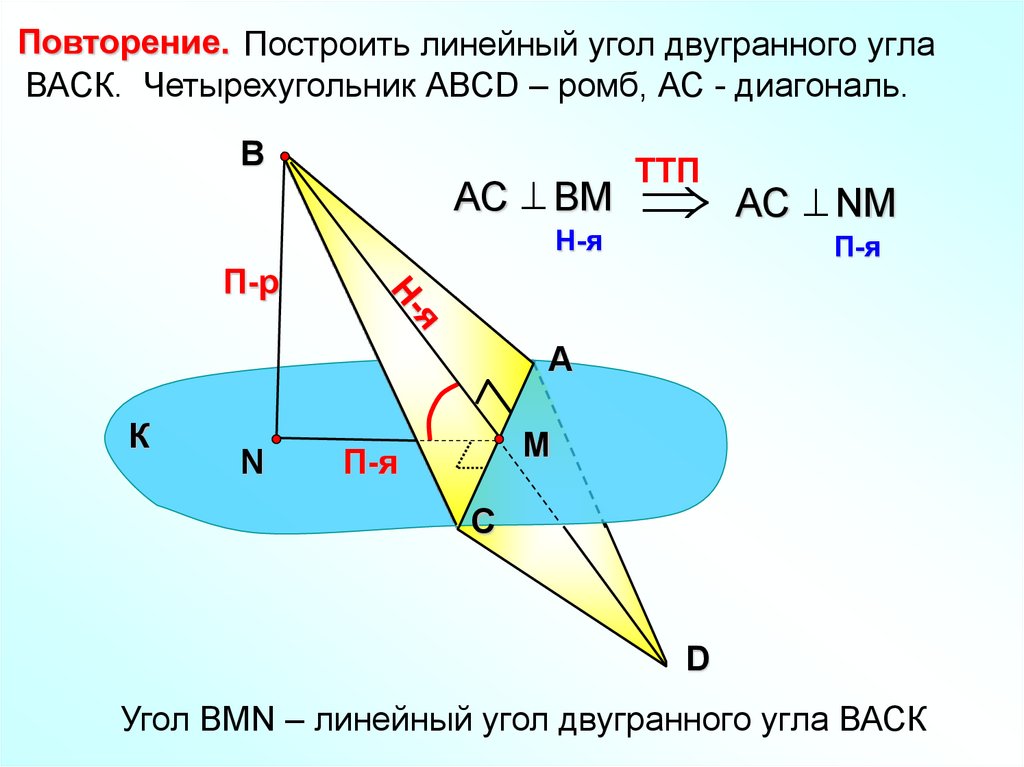
Повторение. Построить линейный угол двугранного угла
ВАСК. Четырехугольник АВСD – ромб, АС - диагональ.
В
АС ВМ
H-я
TTП
АС NМ
П-я
П-р
А
К
N
M
П-я
С
D
Угол ВMN – линейный угол двугранного угла ВАСК

20.

Две пересекающиеся плоскости называются
перпендикулярными (взаимно перпендикулярными),
если угол между ними равен 900.

21.

Признак перпендикулярности двух плоскостей.
Если одна из двух плоскостей проходит через прямую,
перпендикулярную к другой плоскости, то такие
плоскости перпендикулярны.
В
С
D
А

22.

Следствие. Плоскость, перпендикулярная к прямой,
по которой пересекаются две данные плоскости,
перпендикулярна к каждой их этих плоскостей.
a