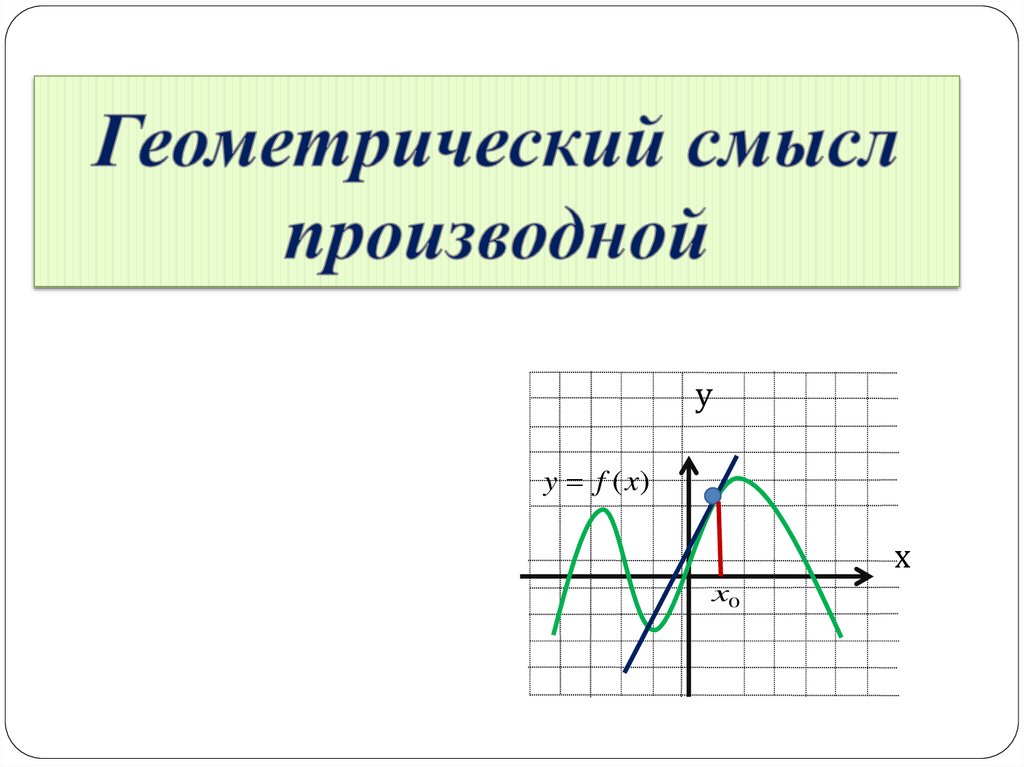
Геометрический смысл производной

1.

у
y f (x)
х
x0

2.

Цель урока:
1. познакомить обучающихся с геометрическим смыслом
производной;
2. формировать умения и навыки обучающихся
применять
полученные
знания
при
решении
упражнений;
3. развивать внимание, память, логическое мышление;
4. формировать умение оценивать свой уровень знаний и
стремление его повышать, способствовать развитию
потребности к самообразованию.
5. воспитывать ответственность, целеустремленность,
умение работать в команде.

3.

«Проверь себя и своего соседа»
1.
2.
3.
4.
5.
6.
7.
8.
9.
x2 +3x
cos2x
(u·v)'
5x
(f(g(x)))'
(xn)'
sinx
(u+v)'
1
2
3
4
5
6
7
8
9
cosx
u' + v'
2x + 3
-2sin2x
x
u'v+uv'
f'(g(x))·g'(x)
5
10.
10 nxn-1
Ответ:
37- 49
58«3»
610
71
«5» 14
- 10 25
б. «4»
9-8 б.
- 7-6
б. 83 96 102

4.

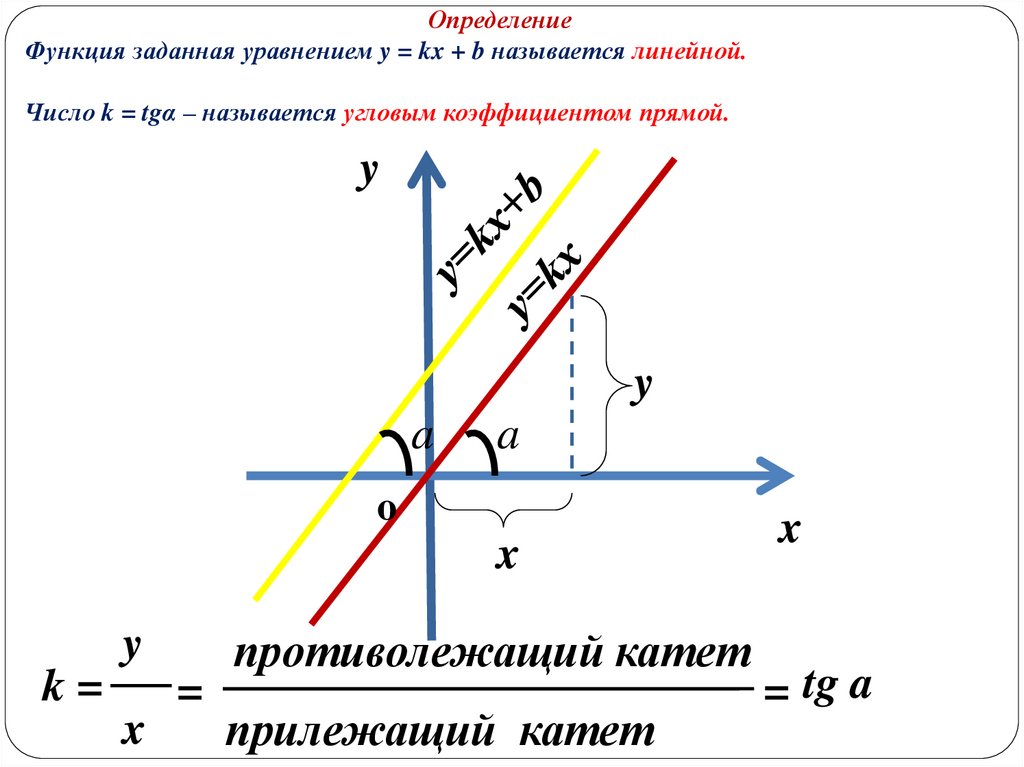
Определение
Функция заданная уравнением y = kx + b называется линейной.
Число k = tgα – называется угловым коэффициентом прямой.
y
y
a
a
o
x
y
k=
x
=
противолежащий катет
прилежащий катет
x
= tg a

5.

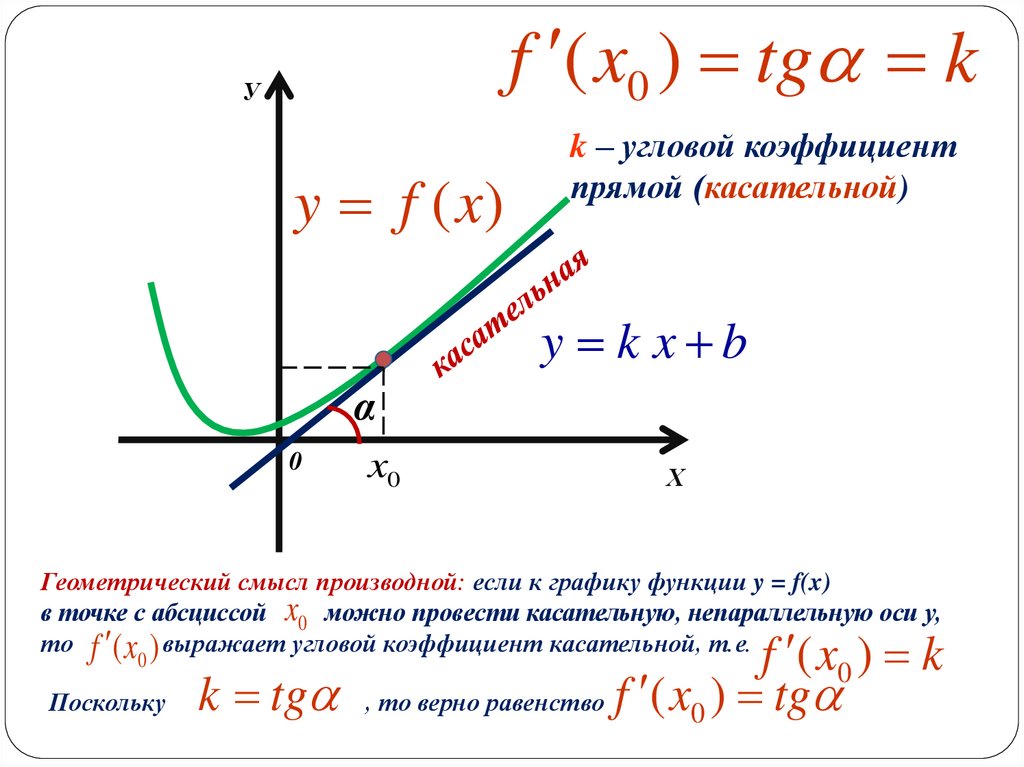
f ( x0 ) tg k
У
y f (x)
k – угловой коэффициент
прямой (касательной)
y k x b
α
0
x0
Х
Геометрический смысл производной: если к графику функции y = f(x)
в точке с абсциссой x0 можно провести касательную, непараллельную оси у,
то f ( x ) выражает угловой коэффициент касательной, т.е.
0
Поскольку
f ( x0 ) k
k tg , то верно равенство f ( x0 ) tg

6.

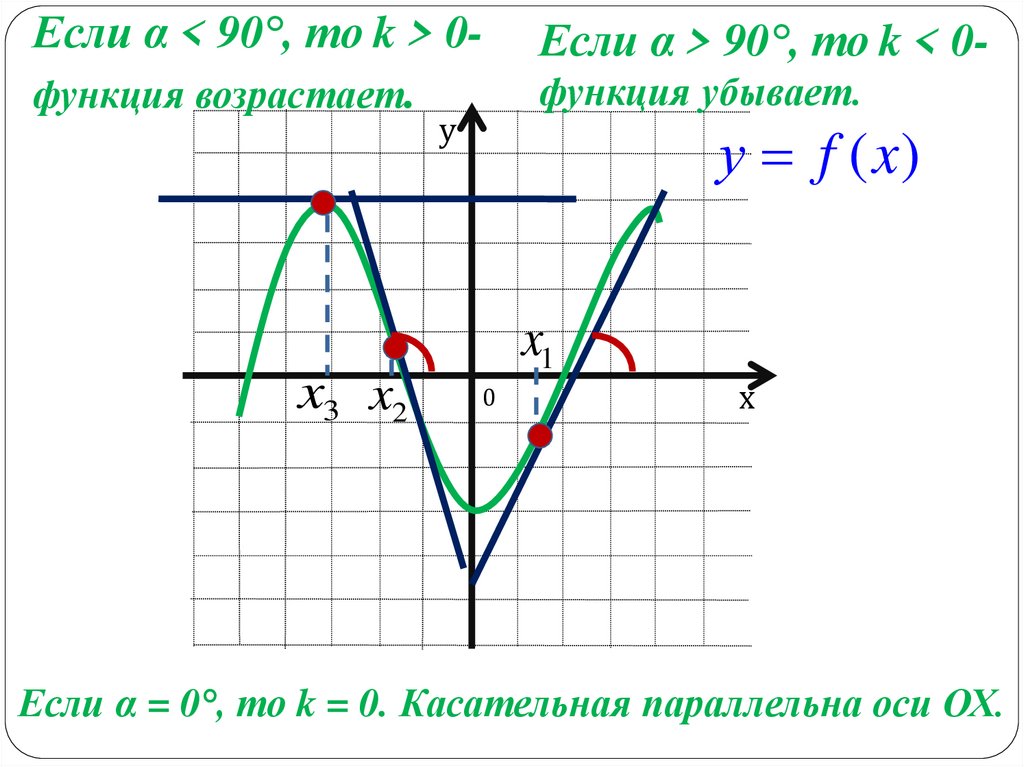
Если α < 90°, то k > 0-
Если α > 90°, то k < 0-
функция возрастает.
функция убывает.
x3 x2
у
у f (x)
x1
0
х
Если α = 0°, то k = 0. Касательная параллельна оси ОХ.

7.

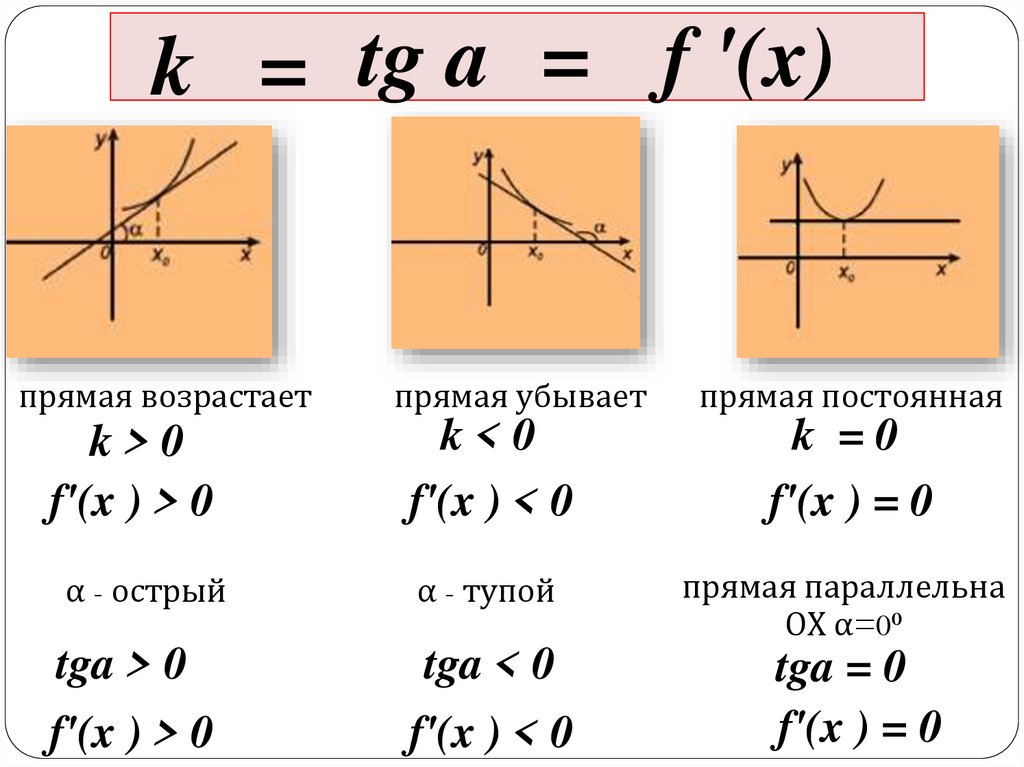
k = tg a = f '(x)
прямая возрастает
k>0
f'(x ) > 0
α - острый
tga > 0
f'(x ) > 0
прямая убывает
прямая постоянная
k<0
f'(x ) < 0
k =0
f'(x ) = 0
α - тупой
прямая параллельна
ОХ α=0⁰
tga < 0
f'(x ) < 0
tga = 0
f'(x ) = 0

8.

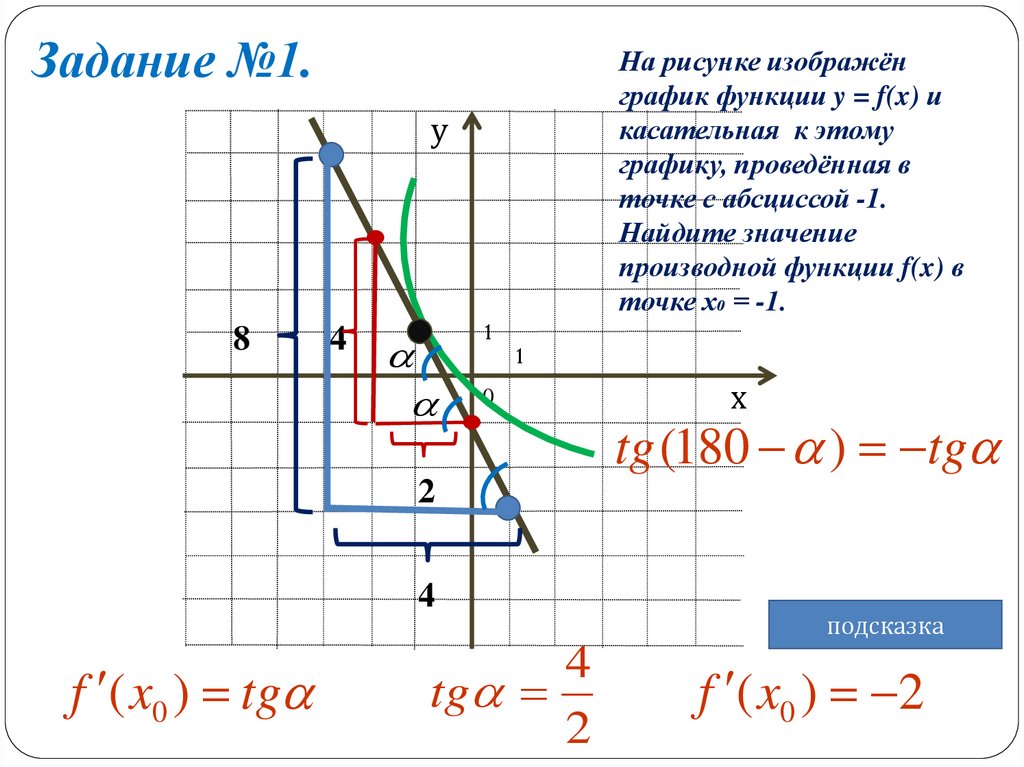
Задание №1.
На рисунке изображён
график функции y = f(x) и
касательная к этому
графику, проведённая в
точке с абсциссой -1.
Найдите значение
производной функции f(x) в
точке х₀ = -1.
у
8
4
1
1
0
х
tg (180 ) tg
2
4
f ( x0 ) tg
4
tg
2
подсказка
f ( x0 ) 2

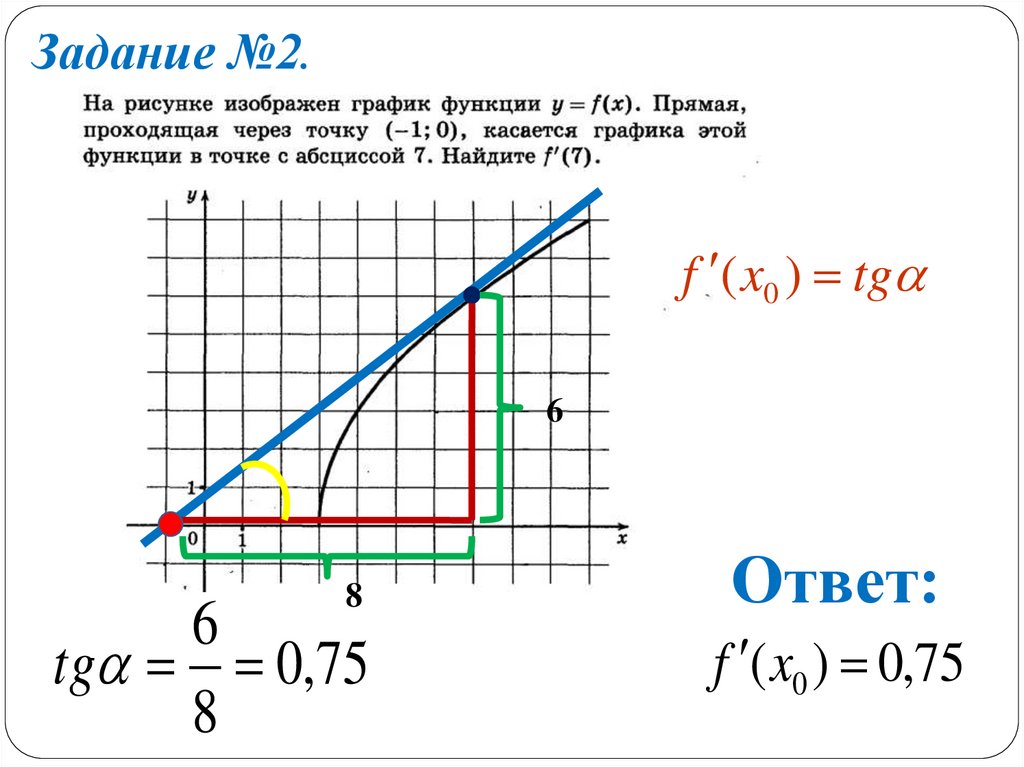
9.

Задание №2.
f ( x0 ) tg
6
8
6
tg 0,75
8
Ответ:
f ( x0 ) 0,75

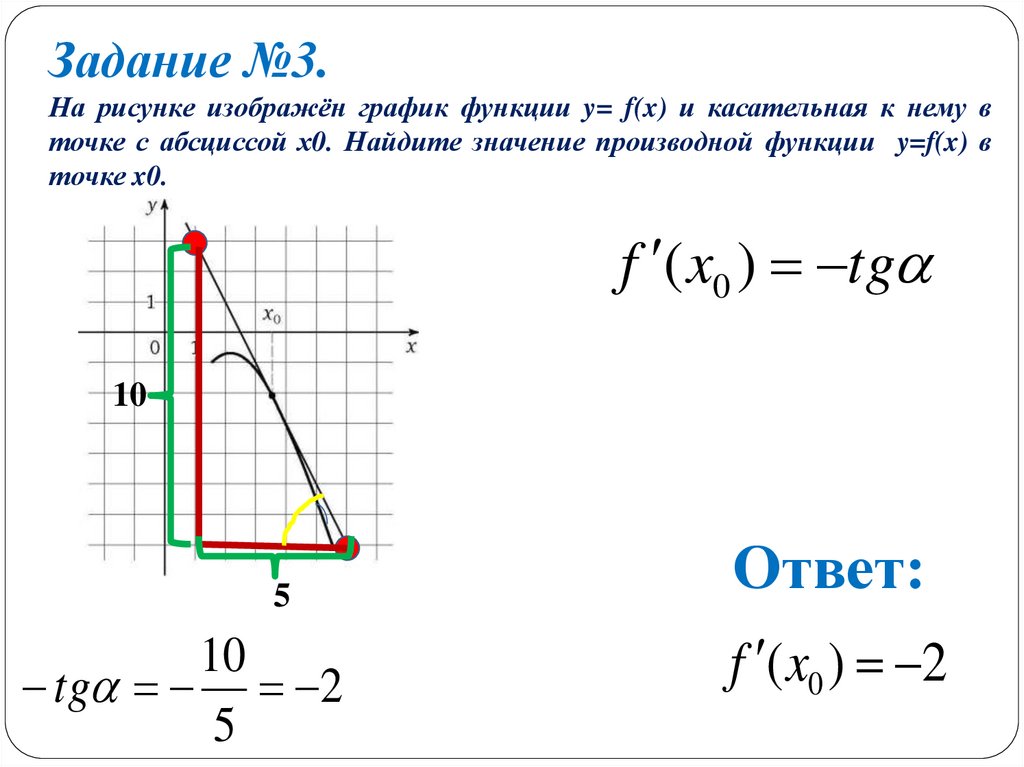
10.

Задание №3.
На рисунке изображён график функции y= f(x) и касательная к нему в
точке с абсциссой х0. Найдите значение производной функции y=f(x) в
точке x0.
f ( x0 ) tg
10
5
10
tg 2
5
Ответ:
f ( x0 ) 2

11.

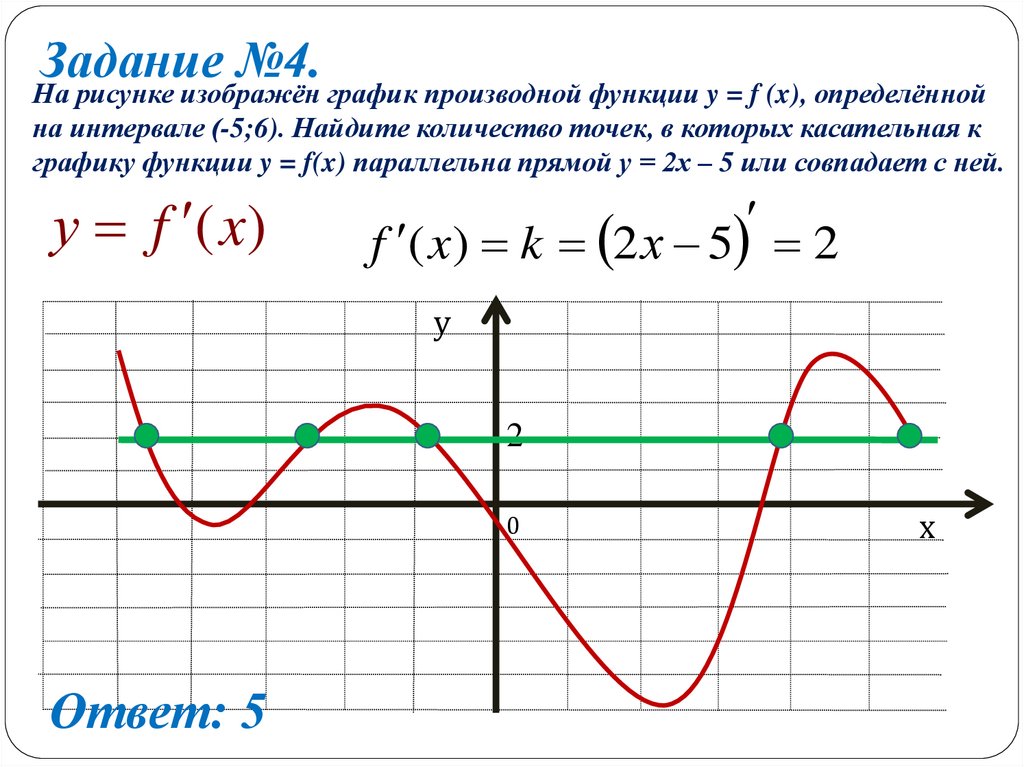
Задание №4.
На рисунке изображён график производной функции y = f (x), определённой
на интервале (-5;6). Найдите количество точек, в которых касательная к
графику функции y = f(x) параллельна прямой у = 2х – 5 или совпадает с ней.
у f (x)
f ( x) k 2 х 5 2
у
2
0
Ответ: 5
х

12.

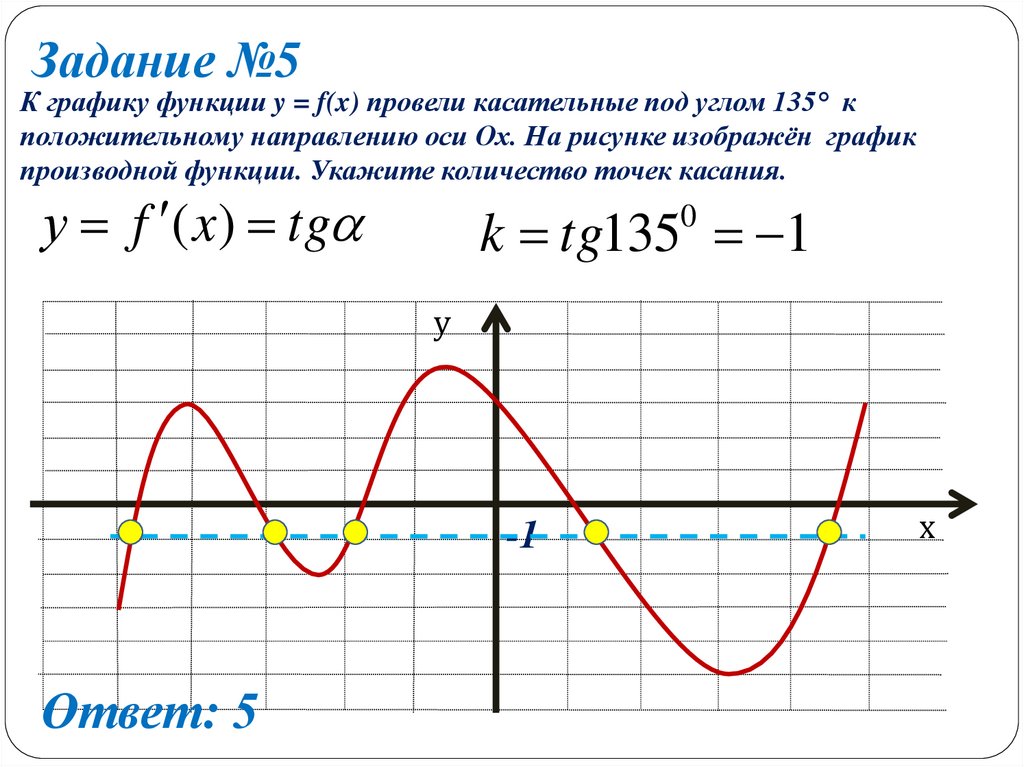
Задание №5
К графику функции y = f(x) провели касательные под углом 135° к
положительному направлению оси Ох. На рисунке изображён график
производной функции. Укажите количество точек касания.
у f ( x) tg
k tg135 1
0
у
-1
Ответ: 5
х

13.

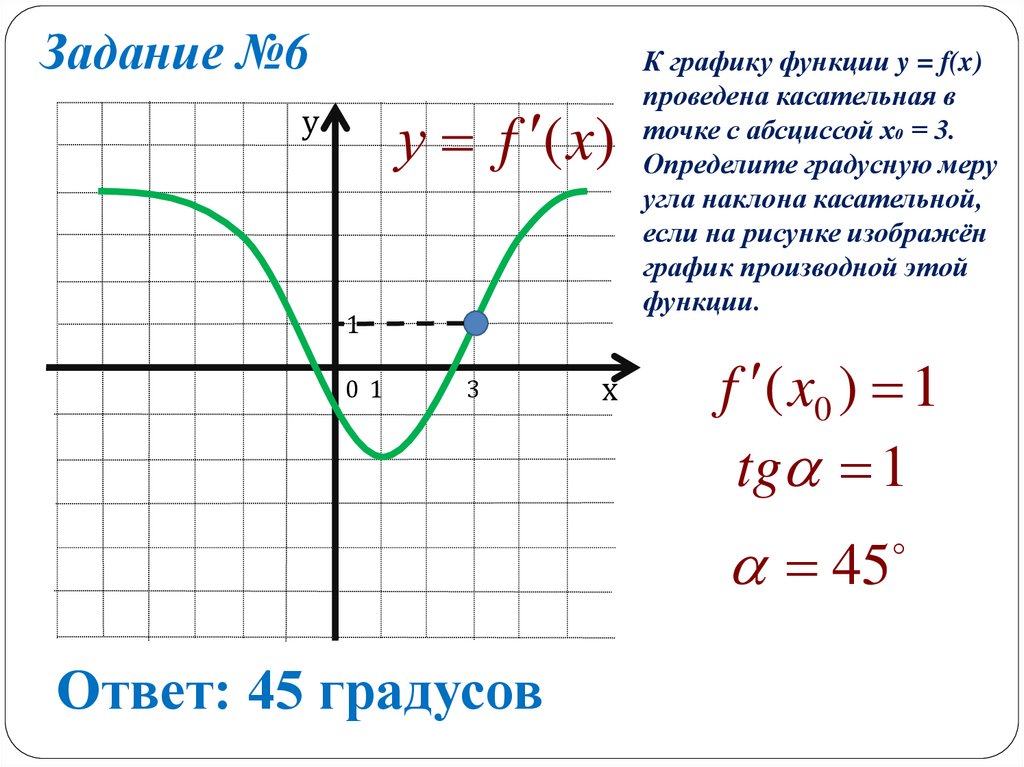
Задание №6
у f (x)
у
1
01
3
х
К графику функции y = f(x)
проведена касательная в
точке с абсциссой х₀ = 3.
Определите градусную меру
угла наклона касательной,
если на рисунке изображён
график производной этой
функции.
f ( x0 ) 1
tg 1
45
Ответ: 45 градусов

14.

Задание №7
Найти угловой коэффициент
касательной, проведенной к графику
функции y=2x+ctgx в точке с абсциссой
Решение.
1. Найдем производную функции:
.
2. Вычислим значение найденной производной в точке х0:
Ответ: k= 1

15.

Задание №8
Найти угол между касательной к графику функции
y= x4 – 2x3 +3 в точке с абсциссой
Решение.
- тангенс угла наклона касательной к
графику функции в определенной точке равен значению производной функции
в этой точке. Найдем производную и подставим вместо х значение
и
осью Ох
f ′(x) = 4x3– 6x2,
tgα = -1, α = 1350.
Ответ: α = 1350

16.

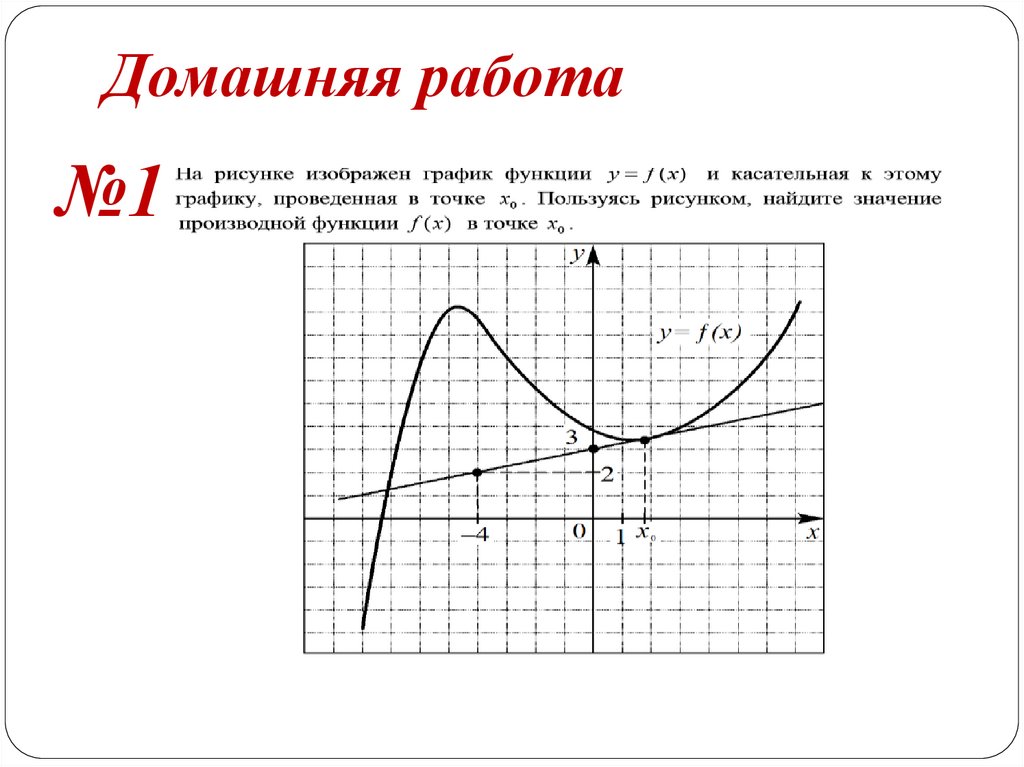
Домашняя работа
№1

17.

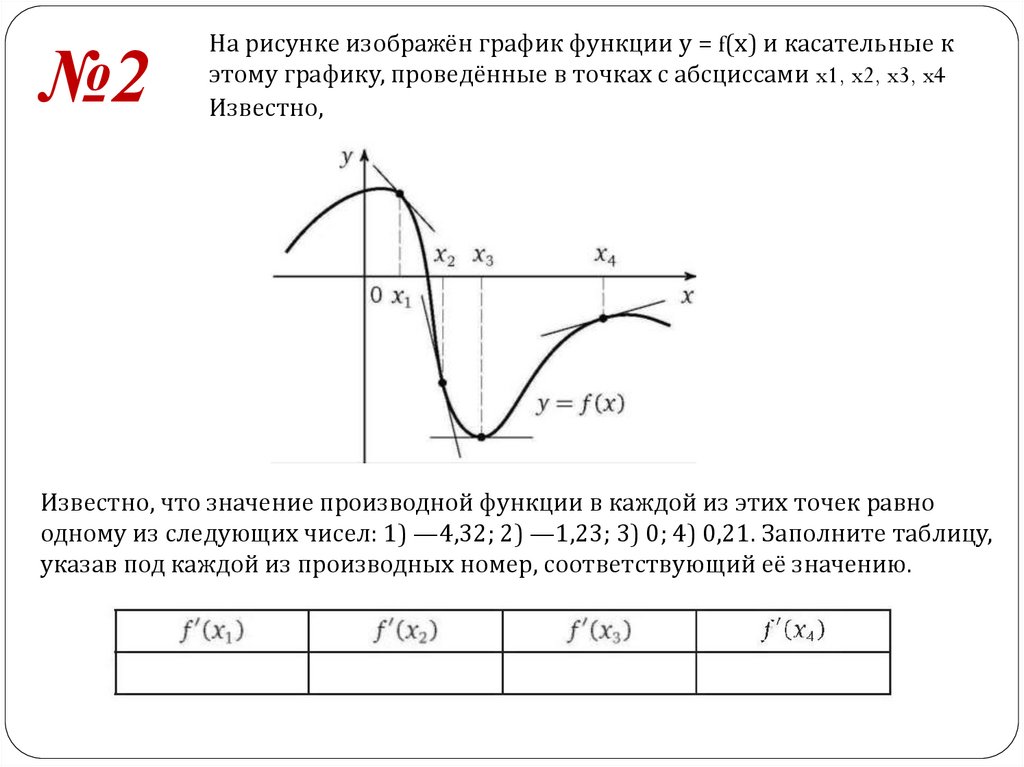
№2
На рисунке изображён график функции у = f(х) и касательные к
этому графику, проведённые в точках с абсциссами x1, x2, x3, x4
Известно,
Известно, что значение производной функции в каждой из этих точек равно
одному из следующих чисел: 1) —4,32; 2) —1,23; 3) 0; 4) 0,21. Заполните таблицу,
указав под каждой из производных номер, соответствующий её значению.

18.

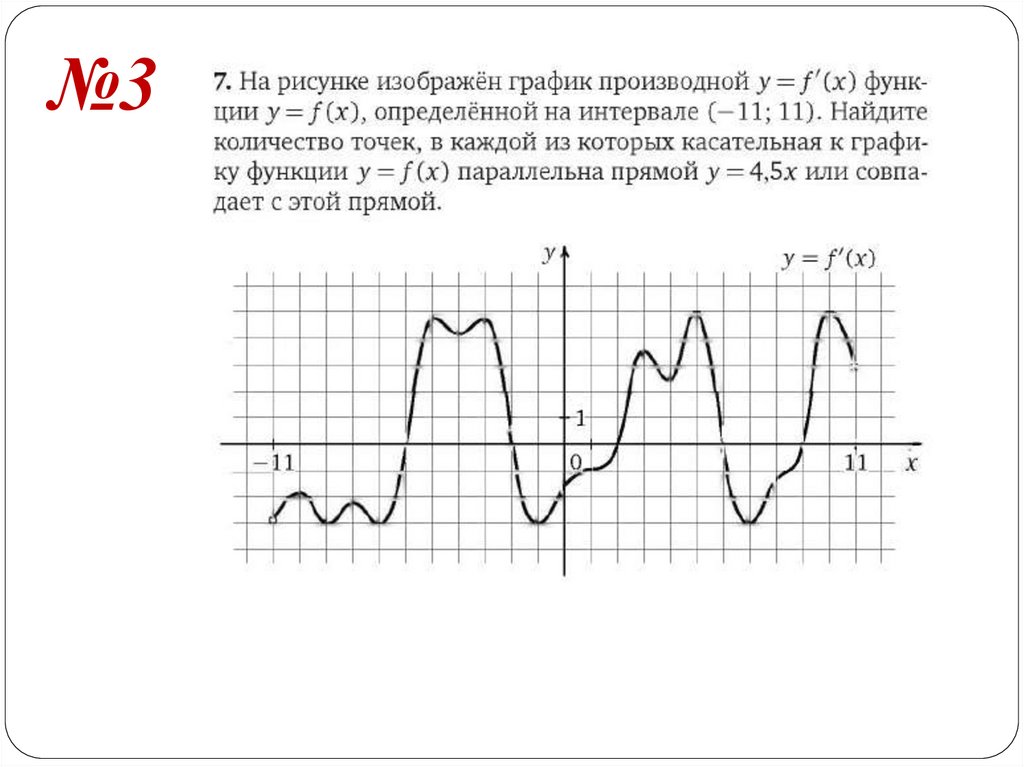
№3

19.

.
№4
Найти угловой коэффициент касательной к графику
функции y= f(x) в точке с абсциссой x0:
A) f(x) = x3, x0=1;
B) Б) f(x) = sinx,