Геометрический смысл производной

1.

Урок № 34

2.

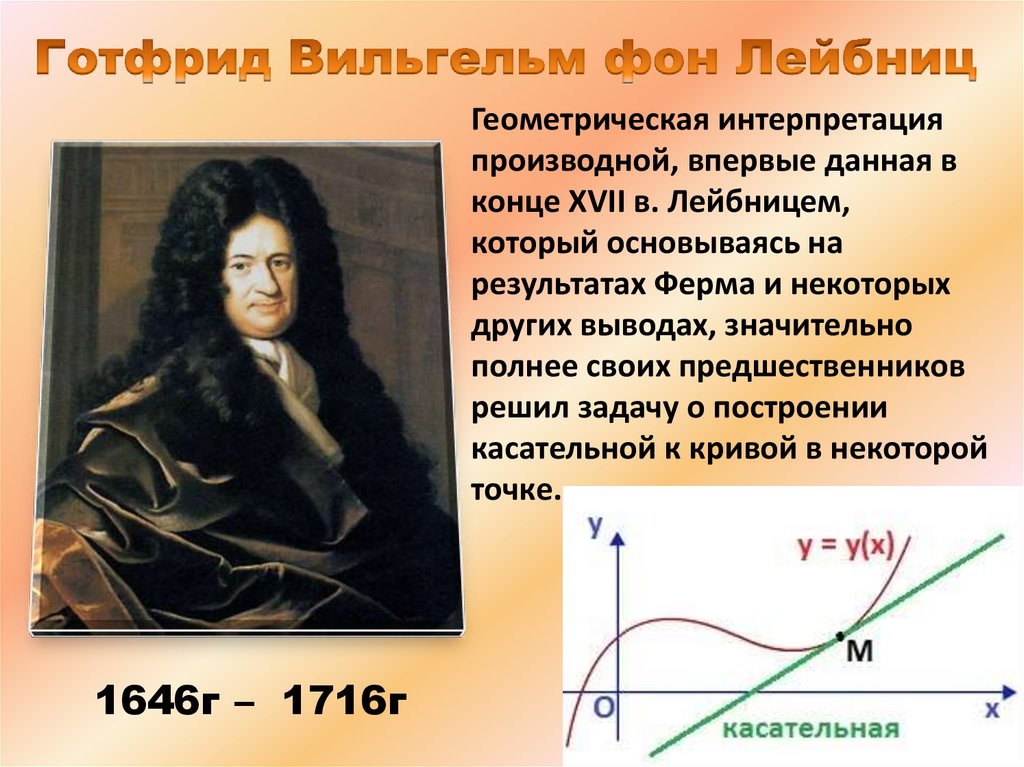
Геометрическая интерпретация
производной, впервые данная в
конце XVII в. Лейбницем,
который основываясь на
результатах Ферма и некоторых
других выводах, значительно
полнее своих предшественников
решил задачу о построении
касательной к кривой в некоторой
точке.
1646г – 1716г

3.

y
y
a
a
o
x
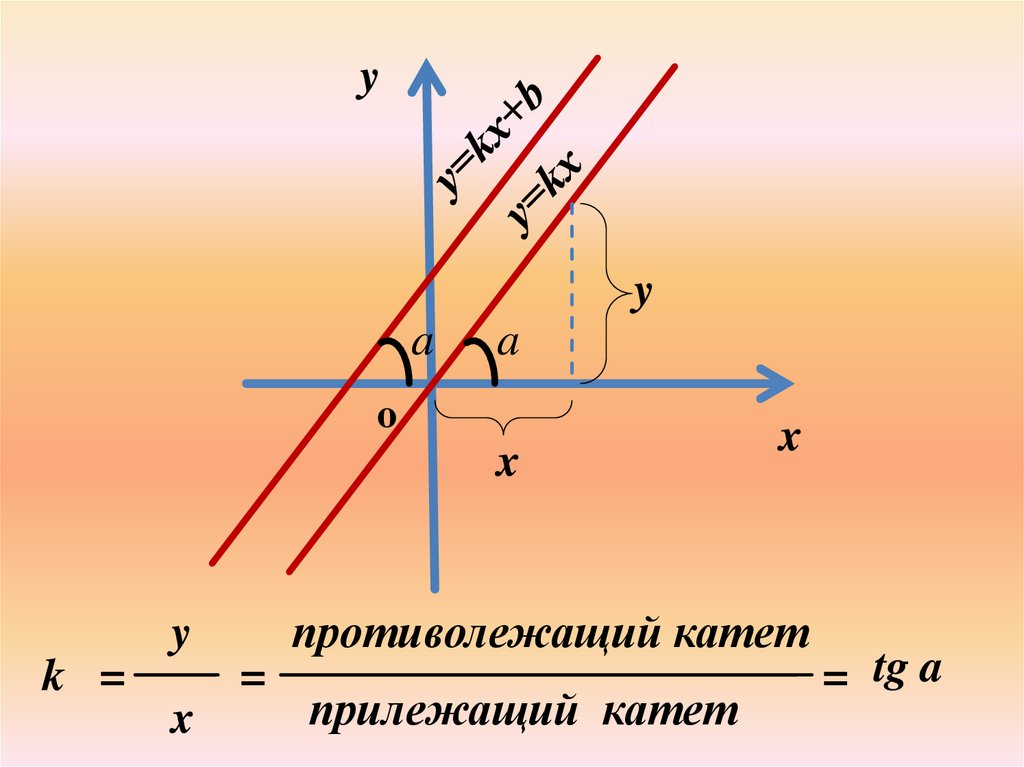
противолежащий катет
y
k =
=
x
x
прилежащий катет
= tg a

4.

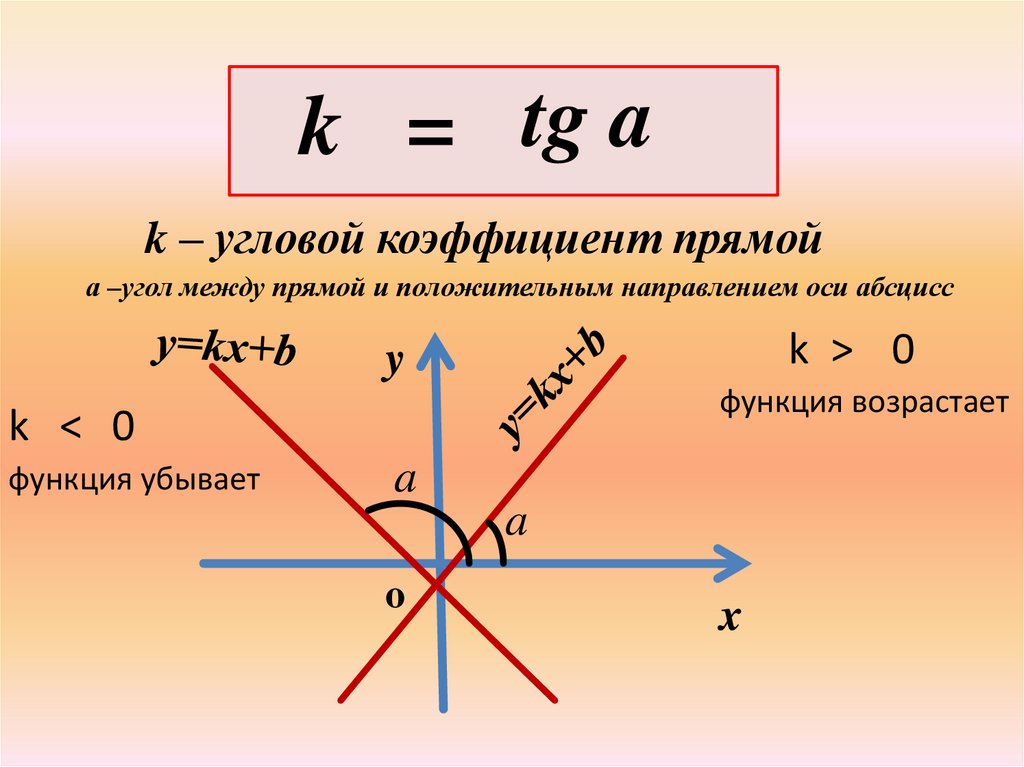
k = tg a
k – угловой коэффициент прямой
а –угол между прямой и положительным направлением оси абсцисс
k > 0
y
функция возрастает
k < 0
функция убывает
a
a
o
x

5.

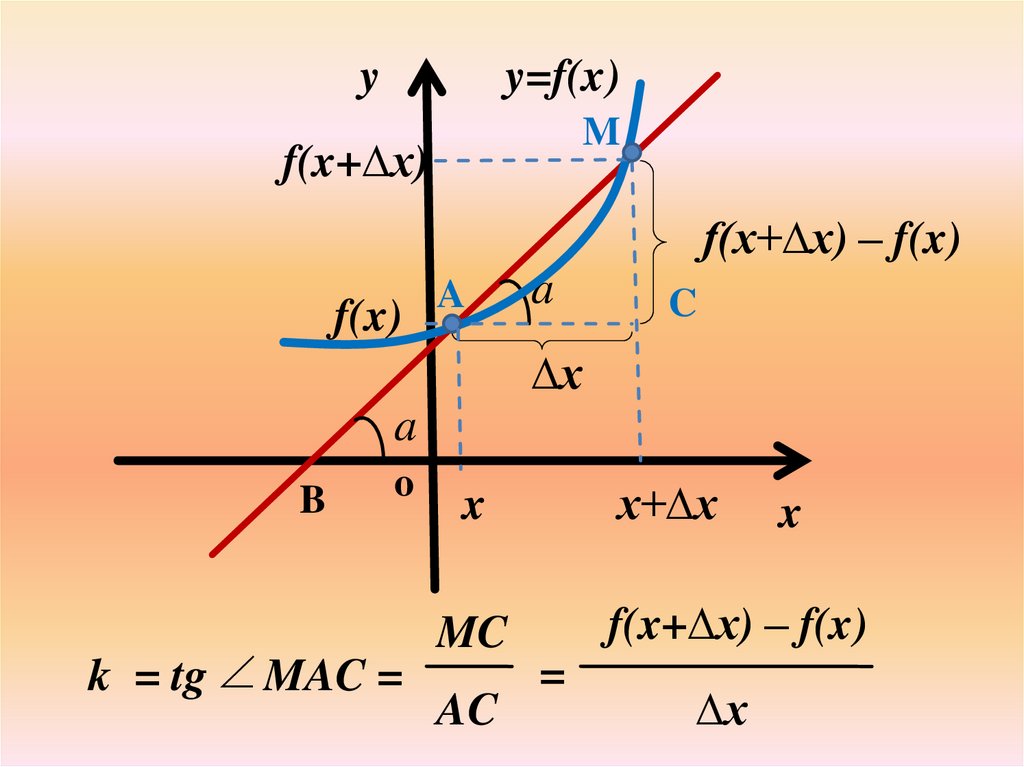
y
y=f(x)
M
f(x+∆х)
f(x+∆х) – f(x)
f(x)
A
a
C
∆х
a
B
o
k = tg MAC =
x
x+∆х
MC
f(x+∆х) – f(x)
AC
=
∆х
x

6.

y
y=f(x)
M
f(x+∆х)
f(x+∆х) – f(x)
f(x)
A
a
C
∆х
x
x+∆х x
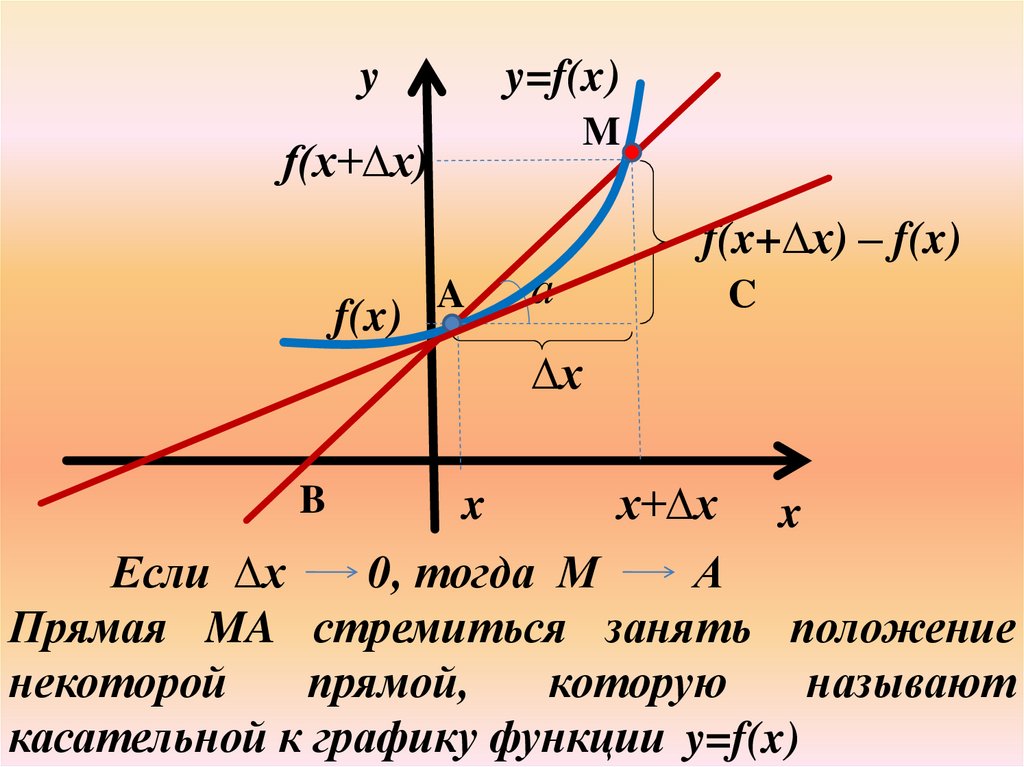
Если ∆х
0, тогда М
А
Прямая MA стремиться занять положение
некоторой
прямой,
которую
называют
касательной к графику функции y=f(x)
B

7.

f(x+∆х)
–
f(x)
lim k = lim
= f ' (x)
∆х 0 ∆х 0
∆х
k = tg a = f ' (x)
Значение производной в точке равно
угловому коэффициенту касательной к графику
функции в этой точке

8.

k = tg a = f ' (x)
прямая возрастает
прямая убывает
прямая постоянная
k>0
f'(x ) > 0
k<0
f'(x ) < 0
k =0
f'(x ) = 0
α - острый
α - тупой
прямая параллельна ОХ
α=0⁰
tga > 0
f'(x ) > 0
tga < 0
f'(x ) < 0
tga = 0
f'(x ) = 0

9.

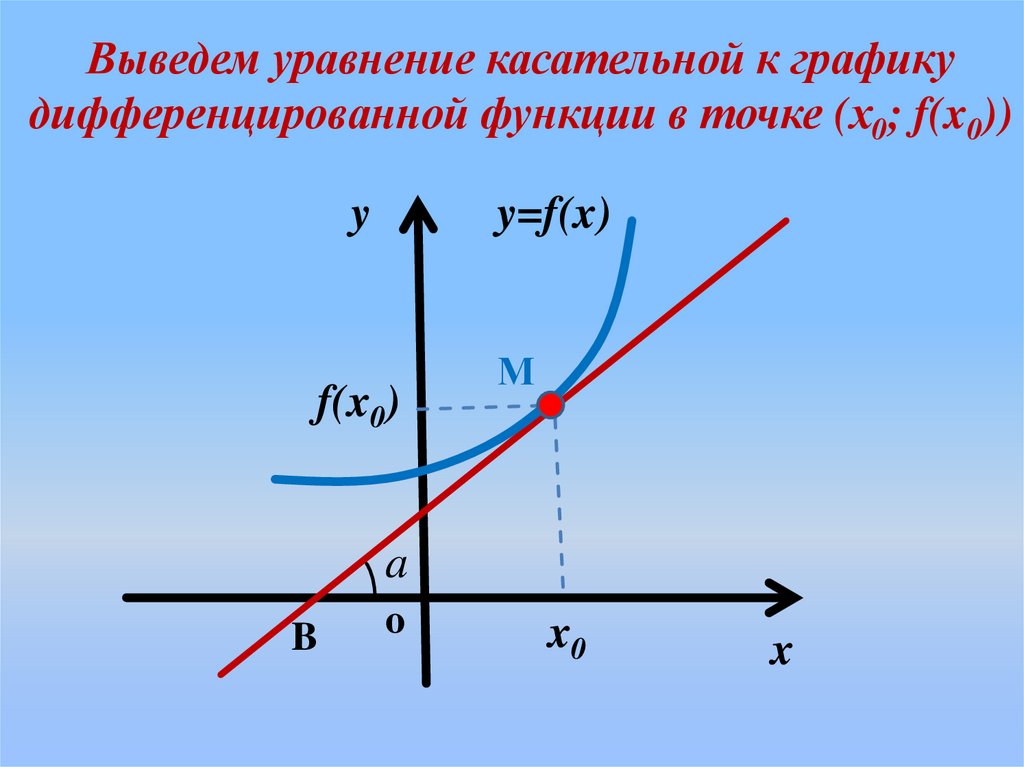
Выведем уравнение касательной к графику
дифференцированной функции в точке (х0; f(x0))
y
y=f(x)
f(x0)
М
a
B
o
x0
x

10.

y=kx +b
(1)
k = tg a = f ' (x)
y=f' (x0 )x+ b
(2)
Т.к. касательная проходит через точку с координатами
(х0; f(x0)) , подставим ее координаты в уравнение (2) и найдем b
f(x0)=f' (x0 )x0+ b
b =f(x0) – f' (x0 )x0
Подставьте в уравнение (2) значение b и сделав
соответствующие преобразования получите:
у = f(x0) + f '(x0)(х – х0)

11.

Алгоритм
нахождения уравнения касательной
к графику функции y=f(x)
в точке с абсциссой х0
1. f(x0) – находим значение функции в данной точке
2. f '(x) – находим производную данной функции
3. f'(x0) - находим значение производной функции в
данной точке
4. Подставляем данные в уравнение касательной к
графику функции
у = f(x0) + f '(x0)(х – х0)

12.

Решаем задачи № 857-861 (только нечетные)