Похожие презентации:
Принятие решений в условиях неопределенности. Игры с природой
1.
Принятие решений в условияхнеопределенности
Игры с природой
1
2.
Понятие «игры с природой».
Особенности платежной матрицы игры с
природой.
Чистые и составные критерии в играх с
природой.
2
3.
Теория игр — это теория математических моделей принятияоптимальных решений в условиях наличия неопределенности и
противоположных интересов у различных сторон конфликта.
Теория игр применяется в вопросах борьбы фирм за рынки, в
явлениях олигополии, в планировании рекламных компаний, при
формировании цен на конкурентных рынках, в обменных и торговых
операциях, в биржевой игре, в анализе коалиционного поведения и
т.д. С позиций теории игр можно рассматривать вопросы
централизации и децентрализации управления производством,
оптимальное
планирование
по
нескольким
показателям,
планирование в условиях неопределенности, порождаемой,
например, техническим прогрессом, преодоление ведомственных
противоречий и другие вопросы.
3
4.
Современный мир – мир потрясений, непредсказуемыхизменений и кризисов. Конфликтная ситуация,
экстремальная, ситуация риска давно заняли свою нишу
в мире научных исследований. Тем не менее,
существует еще много неизученных процессов
человеческой деятельности, и поведение человека в
ситуации
неопределенности
–
тому
пример.
Неопределенность все более становится неотъемлемой
характеристикой жизни в связи с чем очевидна
необходимость понимания поведения человека и
особенностей принимаемых им решений в условиях
неопределенности.
5.
Всякая теоретико-игровая модель обычно отражаетситуацию, в которой взаимодействуют несколько
заинтересованных сторон, чьи интересы не
совпадают. Участвующие в ситуации стороны обычно
называют игроками, а решения, которые способны
принимать игроки, - стратегиями. Цель игры состоит
в поиске оптимальных стратегий участников с
учетом
различных
условий
(уровень
информированности, число разыгрываний, понимание
рациональности поведения и т.д.).
6.
Существуют ситуации, в которых предполагается логичность (рациональность)действий игроков, каждый из которых хочет получить для себя максимум
выгоды. Другая разновидность - так называемые игры с природой.
Обычно описание (формализация ситуации) начинается с построения
платежной матрицы, что является, по существу, наиболее трудоемким этапом
подготовки принятия решения. Ошибки в платежной матрице не могут быть
компенсированы никакими вычислительными методами и приведут к
неверному итоговому результату.
Отличительная особенность игры с природой состоит в том, что в ней
сознательно действует только один из участников, в большинстве случаев
называемый ЛПР (статистик). Второму игроку (природе) не важен результат,
либо он не способен к осмысленным решениям. Например, условия не зависят
от действий игрока, а определяются внешними факторами: реакция рынка,
который не будет вредить одному конкретному игроку, государственная
политика, реальная природа…
7.
Игра, в которой осознанно действует только один изигроков, А (он же ЛПР, активный участник, статистик),
называется игрой с природой.
«Природа», П – это обобщенное понятие второго
участника, не преследующего собственных целей и
не стремящегося обратить в свою пользу ошибки
активного игрока.
Природа может реализовать одно из своих
возможных состояний и не имеет целью получение
выигрыша.
7
8.
Неопределенность в игре с природой – этоситуация, в которой условный противник (среда)
не имеет противоположных интересов, но
выигрыш действующего игрока во многом
зависит от неизвестного заранее состояния
противника.
Причина неопределенности - недостаток
информации о внешних условиях, диктуемых
окружающей средой, и особенностях реализации
решений.
8
9.
Неопределенность может быть следствием многих влиянийсреды, таких, как:
► колебание спроса;
► нестабильность экономической ситуации;
► изменение курса валют;
► колебание уровня инфляции;
► неустойчивая биржевая ситуация;
► изменение политической обстановки;
► форсмажорные обстоятельства;
► погода как природное явление…
9
10.
Примеры ситуаций, которые могут быть смоделированы,как игра с природой (и часто встречаются в задачах):
1. Предприниматель выбирает объем производства, рынок
формирует спрос.
2. Фермер выбирает сельхозкультуры для посева, погода
может реализоваться различная.
3. Менеджер магазина выбирает объем закупок,
покупатели реализуют спрос…
Во всех случаях один игрок разумен (ЛПР), другому
(природа) безразлично.
11.
Платежная матрица - это один из методов отображения информациив ситуации, когда имеется два участника. Он полезен, когда ЛПР
должен установить, какая из его стратегий в наибольшей мере будет
способствовать достижению его цели.
Платеж может выражать величину денежного вознаграждения или
полезность, являющиеся следствием конкретной стратегии в
сочетании с конкретными обстоятельствами. Если платежи
представить в форме таблицы (или матрицы), получаем платежную
матрицу. Матрица показывает, что платеж зависит от определенных
событий, которые могут свершиться.
В платёжной матрице элементами являются числа, выражающие
выигрыши и проигрыши игроков. Выигрыши и проигрыши могут
также выражаться в баллах, других единицах или быть
безразмерными. В игре с природой ее элементы – результаты
только для ЛПР.
12.
Игра с природой представляется в видеплатежной матрицы, элементы которой
аij– выигрыши игрока А, но они не
являются проигрышами природы П.
Ей безразличен результат.
12
13.
3.1. Понятие игры с природойПлатежная матрица еще называется
матрицей доходности (матрицей
выигрышей). Она агрегирует
информацию о возможной
доходности, полезности вариантов
стратегии игрока А при различных
сценариях развития ситуации
(различных состояниях природы).
(Иногда фактически она бывает матрицей убытков, отраженных
положительными величинами, что влияет на форму использования
критериев принятия решения)
13
14.
Для ЛПР результат важен и зависит нетолько от выбранной им стратегии, но и
от заранее неизвестного состояния
природы (при этом список состояний и
величины результатов при сочетании
стратегии ЛПР и состояния природы
известны).
ЛПР
еще
называют
«статистиком», т.к. в некоторых случаях
он может собрать статистику состояний
природы (знать частоты их реализации),
более или менее надежную.
15.
Каждый элемент платежной матрицы aij – выигрышигрока А при стратегии Ai в состоянии природы Пj
П1
выигрыши игрока А
П2
a11 a12
a21 a22
... ...
am1 am 2
…
Пn
... a1n
... a2 n
... ...
... amn
A1
A2
Am
природа (П)
15
16.
3.2. Принятие решений в условиях неопределенностиЕсли будет принято i-e решение, а
состояние внешней среды соответствует
j-й ситуации, то лицо, принимающее
решение, получит доход aij
{выбранная стратегия Аi + реализовавшееся
состояние природы Пj} => результат аij
16
17.
Пример 1 построения платежной матрицы(задание, подобное тому, что в лабораторной работе)
Параметры, в зависимости
от которых платежная
функция принимает
конкретный вид
Пока только построим матрицу платежей!
18.
19.
Эти значения выделены зеленым в итоговой таблице на следующемслайде.
20.
21.
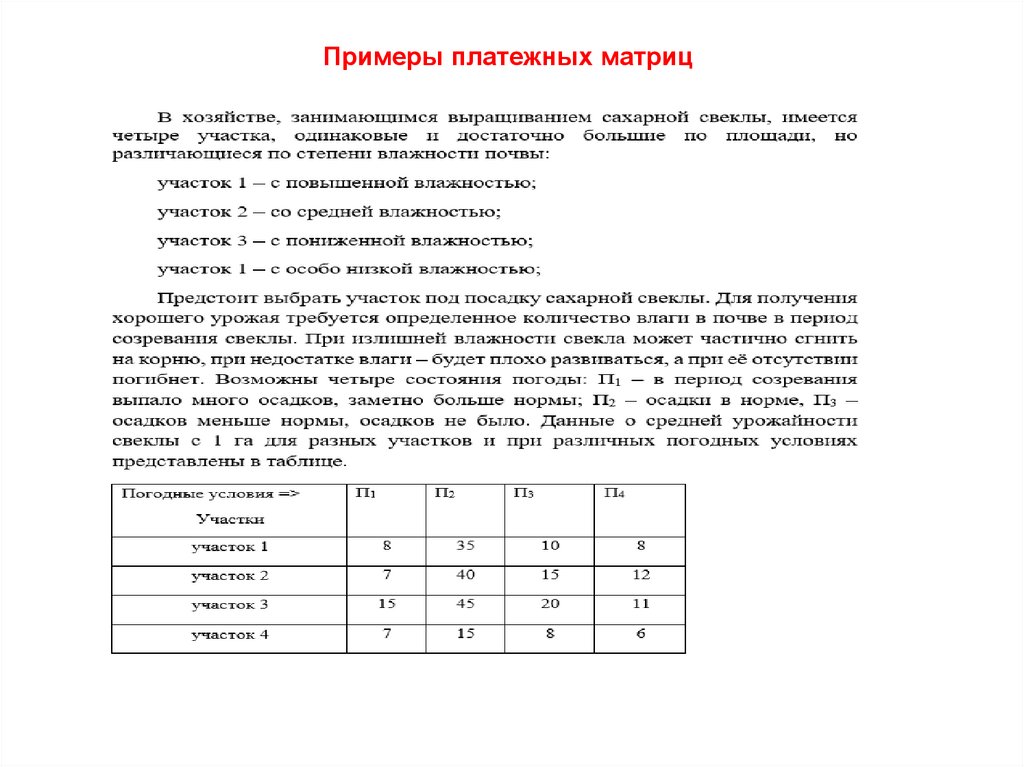
Примеры платежных матриц22.
23.
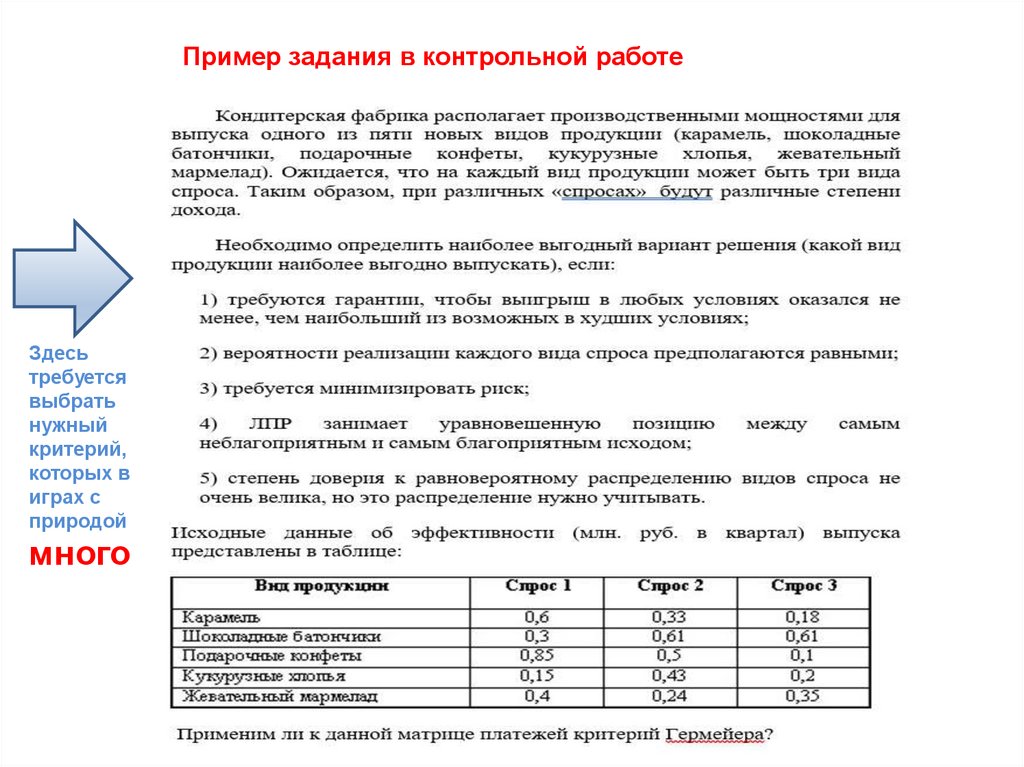
Пример задания в контрольной работеЗдесь
требуется
выбрать
нужный
критерий,
которых в
играх с
природой
много
24.
Пример 2 построения платежнойматрицы
Условие. В новом жилом массиве создается телевизионное ателье
для ремонта в стационарных условиях не более 8 тыс.
телевизоров в год. Для упрощения примем, что поток заявок на
ремонт в условиях стационара выражается числами 2, 4, 6 и 8
тыс. в год. Накопленный опыт аналогичных предприятий
показывает, что прибыль от ремонта телевизора составляет 9 ден.
ед., потери, вызванные отказом в ремонте из-за недостатка
мощностей, оценивается в 5 ден. ед., а убытки от простоя
специалистов и оборудования при отсутствии заявок обходится в
6 ден. ед. в расчете на каждый телевизор. Придав
рассматриваемой ситуации игровую схему, составить платежную
матрицу.
25.
а11 = 2*9;а12 = 2*9 – 5*2 = 8;
а13 = 2*9 – 5*4 =-2;
…
а21 = 2*9 – 6*2 = 6;
а22 = 4*9 = 36;
…
а31 = 2*9 – 6*4 = -6;
…
а43 = 6*9 – 6*2 = 42;
а44 = 8*9 = 72.
Получается матрица:
26.
Обычно, решая игру с природой, ЛПР долженвыбрать
стратегию
с
оптимальным
показателем качества (таковых может оказаться
одна или более, как и критериев качества).
Ситуацию с комбинированием стратегий не
рассматриваем (хотя постановка подобных
задач и методы их решения существуют)!
27.
Различают два вида задачв играх с природой:
1.Задачи о принятии решений в условиях полной
неопределенности,
когда
нет
возможности
получить информацию о вероятностях появления
состояний природы.
2.Задачи о принятии решений в условиях риска,
когда известны вероятности, с которыми природа
может принять каждое своё состояние.
27
28.
Предположим, что лицо, принимающее решение,может выбрать одну из возможных альтернатив,
обозначенных номерами i = 1, 2, …, m
Ситуация является полностью неопределенной,
т. е. известен лишь набор возможных вариантов
состояний внешней (по отношению к лицу,
принимающему решение) среды, обозначенных
номерами j = 1, 2, …, n.
28
29.
Обычно, когда принимается решение вусловиях риска, вероятности состояний среды
хоть как-то могут быть оценены. Если же ЛПР
желает оценить величину риска, не зная их,
строится матрица рисков и применяется
критерий Сэвиджа.
30.
Построение матрицы рисков:Предположим, необходимо провести оценку риска в
условиях, когда реальная ситуация неизвестна. Если
игрок знал бы точно, что осуществится именно j-е
состояние природы, то выбрал бы наилучшее для этого
состояния решение, то есть ту стратегию, которая
принесет наибольший выигрыш при фиксированном j.
Таким образом, выбираются наилучшие результаты в
каждом столбце
bj = max(aij),
i = 1, 2, …, n
и далее будут найдены отклонения от них, составляющие
величины рисков.
30
31.
Принимая i-e решение, игрок А рискует получить не bj, а только aij, тоесть, если игрок примет i-е решение, а в природе реализуется j-е
состояние, то произойдет недополучение дохода в размере:
rij b j aij a max j aij
(по сравнению с тем, как если бы игрок знал точно, что реализуется j-е
состояние природы, и выбрал бы решение, приносящее наибольший доход
bj = max(aij), j = 1, 2, …, n)
amax j
– значение показателя доходности варианта стратегии с
максимальной доходностью из имеющихся i-ых вариантов при наступлении
j-ого сценария развития событий
aij - значение показателя доходности i-ого варианта стратегии при
наступлении
j-ого сценария развития событий (элемент платежной
матрицы).
31
32.
R=где
r11
...
r
i1
...
r
m1
... r1 j
... ...
... rij
... ...
rmj
... r1n
... ...
... rin
... ...
rmn
rij b j aij a max j aij
32
33.
Матрица рисков отражает риск (упущеннуювыгоду) от реализации вариантов стратегии
для каждой альтернативы развития
событий, т.е. риск выбора определенного
варианта стратегии.
Ее особенность: любой ее элемент больше
или равен нулю.
34.
При решении задачи о принятии решений вусловиях неопределенности для отбора вариантов
стратегии применяют так называемые критерии
оптимальности, т.е. правила, позволяющие указать
способ выбора наилучшего для ЛПР решения с
учетом особенностей ситуации принятия решения
(информированность ЛПР, склонность его к риску,
желание получить гарантированный результат,
уровень доверия к имеющейся информации и т.д.).
Результаты при применении различных критериев
(рекомендованные к выбору стратегии) могут
различаться!
34
35.
3.2. Принятие решений в условиях неопределенностиДля выбора наиболее эффективного варианта
стратегии ко всем возможным вариантам развития
ситуации рекомендуется применить несколько
критериев. Оптимальной разумно считать ту
стратегию из имеющихся, на которую укажет
большинство критериев
(если таковая
имеется). При наличии нескольких наилучших
вариантов с одинаковой частотой ЛПР может
поставить дополнительные требования (или
«бросить жребий»).
35
36.
Простые (чистые) критерии в играх сприродой
К ним относятся:
1) критерий Вальда;
2) критерий максимакса;
3) критерий Байеса;
4) критерий Лапласа;
5) критерий Сэвиджа.
Замечание: принятие решений в условиях риска
происходит при применении критерия Байеса.
Оценка же самой величины риска дается в критерии
Сэвиджа, а максимальный риск весьма часто имеет
место при применении критерия максимакса.
37.
1) Критерий Вальда (другие названия: критерийгарантированного
результата,
максиминный
критерий, пессимистический критерий) предполагает,
что природа, как активный участник (враг), стремится
реализовать наихудшее состояние для ЛПР при
выбранной им стратегии. Он рекомендует выбирать
наибольший элемент платежной матрицы из её
минимально возможных элементов:
W = max min a ij ,
i
здесь
j
a ij – элементы платежной матрицы.
37
38.
Критерий Вальда предназначен для выбора израссматриваемых вариантов стратегий варианта с
наибольшим
показателем
эффективности
из
минимально возможных показателей для каждого
из этих вариантов (принцип: «лучшее их худших»).
Данный
критерий
обеспечивает
максимизацию
минимального выигрыша, который может быть получен
при реализации каждого из вариантов стратегий.
Критерий ориентирует лицо, принимающее решение, на
осторожную линию поведения, направленную на получение
дохода и минимизацию возможных рисков одновременно.
38
39.
Применение критерия Вальда оправдано, еслиситуация, в которой принимается решение,
характеризуется следующими обстоятельствами:
► о вероятности наступления того или иного
состояния природы ничего не известно;
► требуется максимально снизить риск и
гарантировать неуменьшаемый результат;
► реализуется малое количество решений (в
идеале: решение принимается один раз).
39
40.
Тип товараА1
А2
А3
П1
Спрос
П2
П3
20
16
13
15
12
18
10
14
15
В строках платежной матрицы выделены наименьшие
платежи, из которых ЛПР разумно предпочтет наибольший.
40
41.
W max min aij max( 10;12;13) 13i
j
Обычно минимальные элементы строк записывают в
добавочный
столбец
платежной
матрицы.
Полученный результат соответствует стратегии А3 .
41
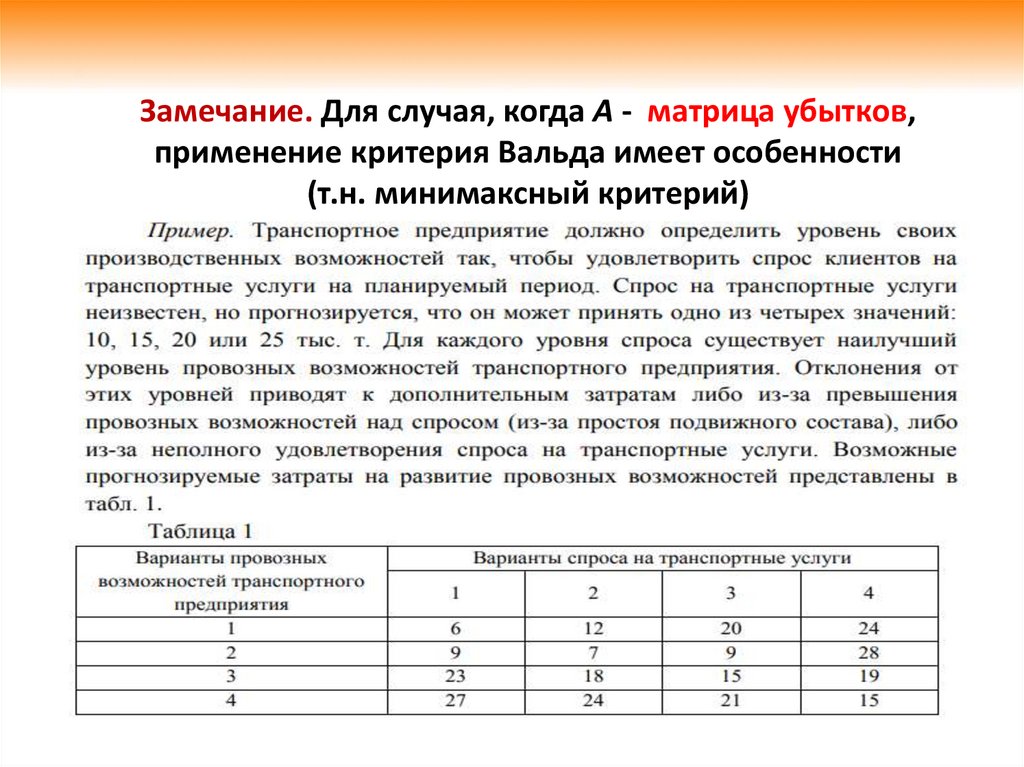
42.
Замечание. Для случая, когда А - матрица убытков,применение критерия Вальда имеет особенности
(т.н. минимаксный критерий)
43.
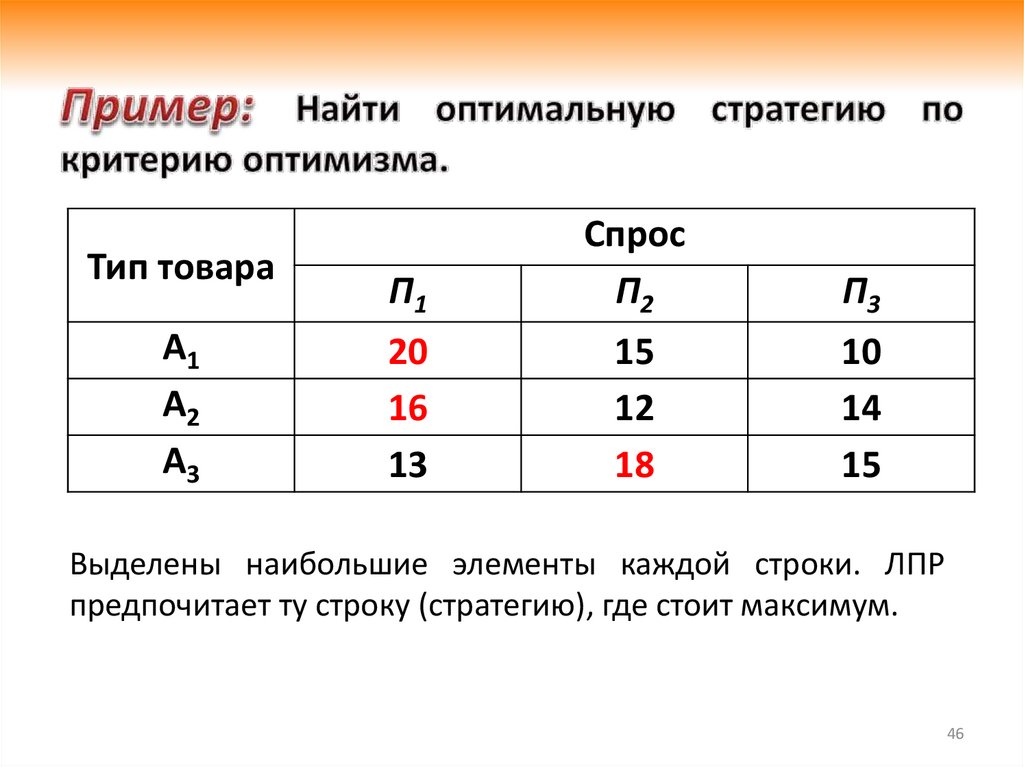
44.
2) Критерий крайнего оптимизма (критериймаксимакса) рекомендует ЛПР для выбора ту ее
стратегию, которая содержит в соответствующей
строке платежной матрицы наибольший элемент из
всех её максимально возможных в каждой строке
элементов:
M = max max a ij ,
i
j
44
45.
Данный критерий предполагает, что развитиеситуации будет максимально благоприятным
для лица, принимающего решение (природа –
«друг» ЛПР, она реализует самую выгодную
ему
стратегию).
Вследствие
этого,
оптимальным выбором будет вариант с
наибольшим
значением
показателя
эффективности в матрице доходности.
45
46.
Тип товараА1
А2
А3
П1
Спрос
П2
П3
20
16
13
15
12
18
10
14
15
Выделены наибольшие элементы каждой строки. ЛПР
предпочитает ту строку (стратегию), где стоит максимум.
46
47.
M max max aij max( 20;16;18) 20i
j
Полученный результат соответствует
стратегии А1
Замечание: минимальный платеж (10) также стоит в первой
строке, поэтому выбирая первую стратегию, игрок рискует как
максимально выиграть, так и максимально проиграть. Критерий
максимакса – часто самый рискованный. Насколько силен
(вероятен) риск, зависит от вероятностей состояний природы,
но про них ничего пока не известно.
47
48.
3) Критерий Сэвиджа (критерий минимаксного рискаСэвиджа) предписывает выбирать минимальный из
максимальных элементов по строкам матрицы рисков:
S = min max r ij ,
i
j
Здесь и нужна
матрица рисков,
чье определение
дано на сл. 30-32.
Среди элементов матрицы рисков сначала выбирается
максимальный риск, соответствующий каждой стратегии, а
затем из них выбирается наименьший. Пессимистично
настроенный игрок предполагает, что состояние природы будет
таковым, что для любой его стратегии риск будет наибольшим, а
стратегию выбирает такую, чтобы этот риск минимизировать.
48
49.
Критерий Сэвиджа позволяет выбрать вариантстратегии с меньшей величиной риска по
сравнению с более высоким, первоначально
ожидаемым уровнем риска.
Данный критерий ориентирует лицо принимающее
решение на более благоприятное развитие ситуации по
сравнению с наихудшим состоянием, на которое то
рассчитывало вначале. Критерий имеет сходство с
критерием Вальда (пессимизм), но в некоторых случаях эти
критерии указывают на различные оптимальные
стратегии.
49
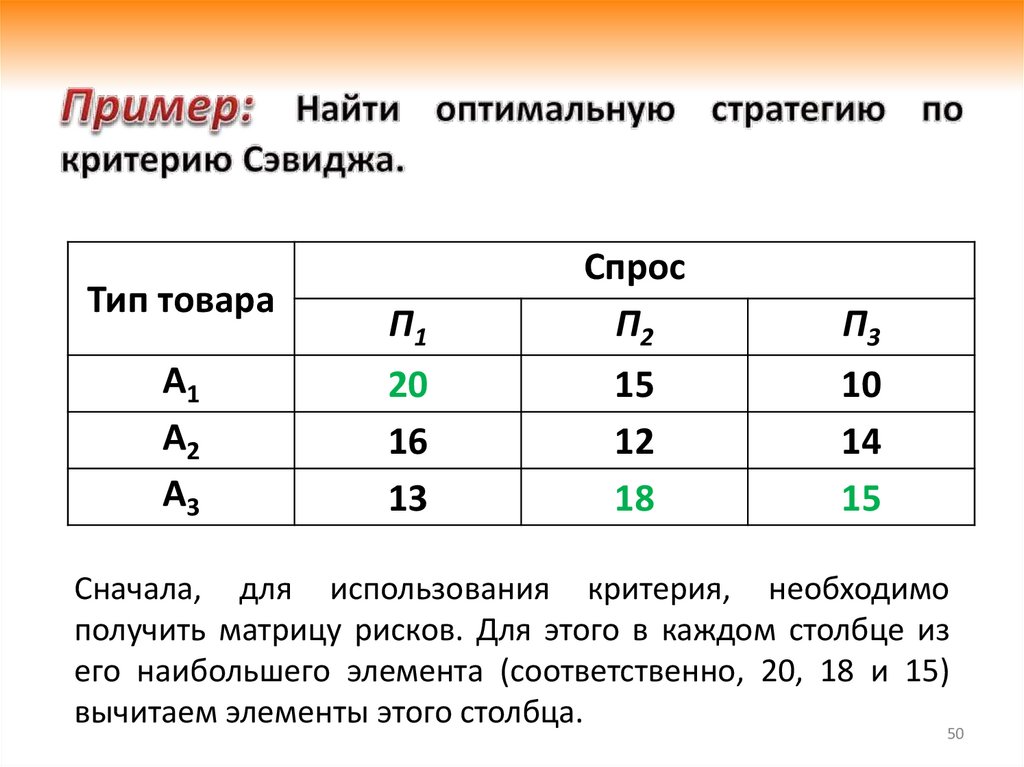
50.
Тип товараА1
А2
А3
П1
Спрос
П2
П3
20
16
13
15
12
18
10
14
15
Сначала, для использования критерия, необходимо
получить матрицу рисков. Для этого в каждом столбце из
его наибольшего элемента (соответственно, 20, 18 и 15)
вычитаем элементы этого столбца.
50
51.
Применяя формулу rij = amaxj - aij, построим матрицу рисков R:R=
Тип
товара
А1
А2
А3
Спрос
П1
П2
П3
0
4
7
3
6
0
5
1
0
S min max rij min( 5 ;6 ;7 ) 5
i
Полученный
стратегии А1.
j
результат
соответствует
выбору
51
52.
4) Критерий Байеса (в некоторых источниках – критерийБайеса-Лапласа) отступает от условий полной
неопределенности. Он предполагает, что возможным
состояниям природы можно приписать (узнать, собрав
статистику)
определенную
вероятность
их
наступления и, определив математическое ожидание
выигрыша для каждого решения, выбрать то, которое
обеспечивает наибольшее значение выигрыша с учетом
этих вероятностей. То есть, основываясь на
предыдущих наблюдениях, ЛПР может прогнозировать
будущее состояние природы (статистический принцип).
Вероятности наступления состояний природы Пj
обозначим qj (сумма qj должна быть равна 1!).
53.
Правило, в соответствии с которым принимаетсярешение:
В скобках стоит мат.ожидание М(Аi)
H = max max a ij+ 1 min a ij ,
i
j
j
Фактически, ЛПР ориентируется
на максимальное
математическое ожидание платежей, соответствующих
стратегиям Аi, учитывая все возможные состояния природы.
53
54.
3.2. Принятие решений в условиях неопределенностиКритерий Байеса
предъявляет к ситуации,
принимается решение, следующие требования:
в
которой
– вероятности qj появления состояний Пj известны и не зависят от
времени;
– решение реализуется (теоретически) бесконечно много раз;
– для малого числа реализаций решения допускается некоторый риск.
При достаточно большом количестве реализаций среднее значение
постепенно стабилизируется. Поэтому при полной (бесконечной)
реализации какой-либо риск исключён. Исходная позиция
применяющего – критерий оптимистичнее, чем в случае критерия
Вальда, однако она предполагает более высокий уровень
информированности ЛПР и достаточно длинные реализации.
Недостаток: трудности могут возникнуть при сборе и оценке
статистических данных. Это один из критериев, требующий от ЛПР
повышенной информированности.
54
55.
Пусть вероятности состояний природы (спроса) следующие:Находим математические ожидания по элементам строк:
Замечание.
Обычно
вероятности
больше для
средних
состояний
природы, и
меньше – для
крайних. В
последнем
столбце стоят
суммы
произведений
элементов строк
на
соответствующие
вероятности.
По результатам расчетов рекомендуется выбрать третью стратегию как
оптимальную.
55
56.
3.2. Принятие решений в условиях неопределенности5)Критерий Лапласа.
В
ряде
случаев
представляется
правдоподобным следующее рассуждение:
если информации о вероятностях состояний
природы нет, состояния природы можно
считать
равновероятными.
Этот
предположение
называют
«принципом
недостаточного основания» Лапласа. ЛПР как
бы
искусственно
добавляет
статистику
появлений Пj, тем самым увеличивая риск,
если эта статистика далека от истины.
56
57.
Правило выбора:58.
все qj = 1/3, ищемПолученный результат соответствует стратегии А3
58
59.
Заметим, что гипотеза о равновероятностисостояний
природы
искусственной,
поэтому
является
довольно
принципом
Лапласа
можно пользоваться лишь в ограниченных
случаях. В более общем случае следует считать,
что состояния природы не равновероятны и
использовать для решения критерий Байеса,
если это возможно.
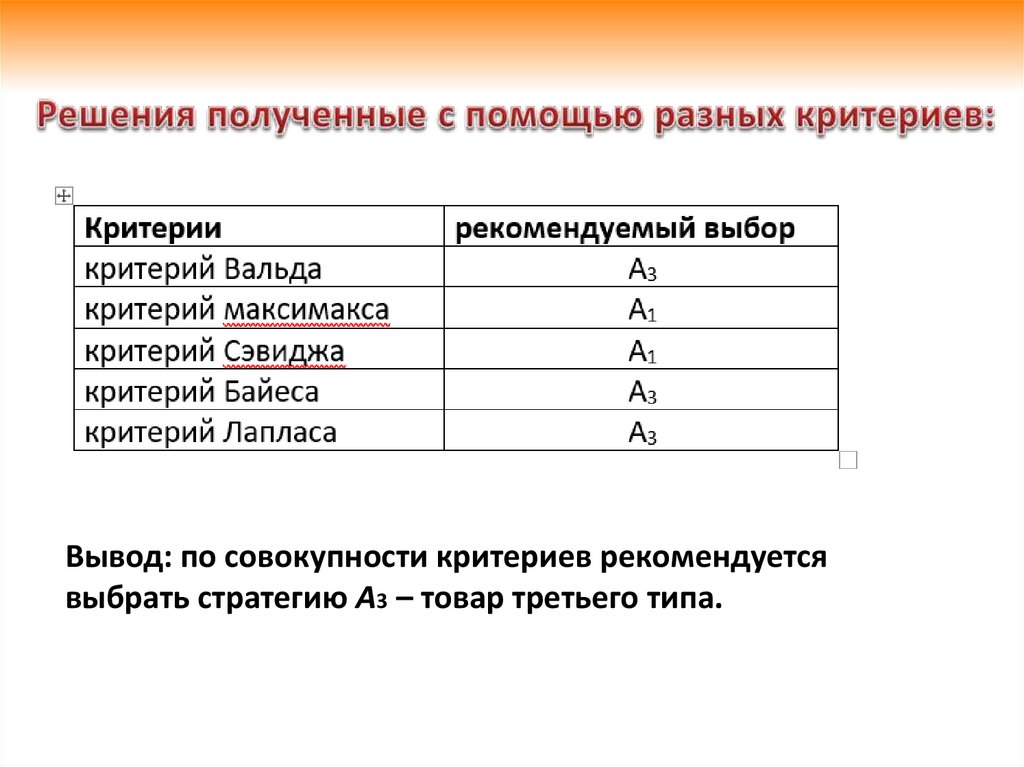
60.
Вывод: по совокупности критериев рекомендуетсявыбрать стратегию А3 – товар третьего типа.
61.
Замечание.Большое число критериев, используемых в
«играх с природой» при принятии решений
(в отличии от антагонистических и
биматричных
игр,
где
главное
–
максимизировать
выигрыш
или
минимизировать убыток) – не недостаток
Теории игр. Оно объясняется различными
типами поведения ЛПР и особенностями
состояний природы (склонность к риску,
информированность, число разыгрываний).
62.
Производные (составные) критериив играх с природой
К ним относятся:
1) критерий Гурвица;
2) критерий Ходжа-Лемана;
3) критерий Гермейера;
4) критерий произведений.
63.
Предположим, ЛПР не может сделать окончательныйвыбор между ситуациями оптимизма и пессимизма.
Представляется логичным, что при выборе решения
вместо одной из двух крайностей в оценке ситуации
разумно придерживаться некоторой промежуточной
позиции, учитывающей возможность как наихудшего,
так и наилучшего, благоприятного поведения
природы. Такой компромиссный вариант и был
предложен Гурвицем.
Леонид Абрамович Гурвич (21 августа 1917-24 июня 2008) американский экономист российско-еврейского происхождения,
почётный профессор Университета Миннесоты. Работал в Комиссии
Коулса, лауреат премии по экономике памяти Альфреда Нобеля за 2007
год за работу совместно с Эриком Маскиным и Роджером Майерсоном
над теорией оптимальных механизмов. Старейший экономист,
получивший премию памяти Альфреда Нобеля (это произошло в 90
лет).
64.
3.2. Принятие решений в условиях неопределенности1. Критерий Гурвица ориентирован на
установление баланса между случаями
крайнего пессимизма и крайнего оптимизма
при выборе стратегии путем взвешивания
обоих исходов с помощью коэффициента
оптимизма.
Он позволяет избежать пограничных
состояний при принятии решения –
неоправданного оптимизма и крайнего
пессимизма и выбрать наиболее вероятный
вариант
стратегии,
обеспечивающий
наилучшую эффективность.
64
65.
Величину λ называют коэффициентом оптимизма, а также коэффициентом доверия или коэффициентом пессимизма.66.
КритерийГурвица
как
бы
«взвешивает»
пессимистический и оптимистический подходы к
анализу неопределенной ситуации. Он предназначен
для выбора некоторого среднего элемента матрицы
доходности, отличающегося от крайних состояний –
от минимального и максимального элементов:
(это одна из 2-х возможных его форм)
где
λ – коэффициент оптимизма, 0 1
67.
Коэффициентλ
выражает
количественно
«меру
оптимизма» игрока А при выборе стратегии и
определяется им из субъективных соображений на основе
статистических исследований результатов принятия
решений или личного опыта лица принимающего решение
в схожих ситуациях.
67
68.
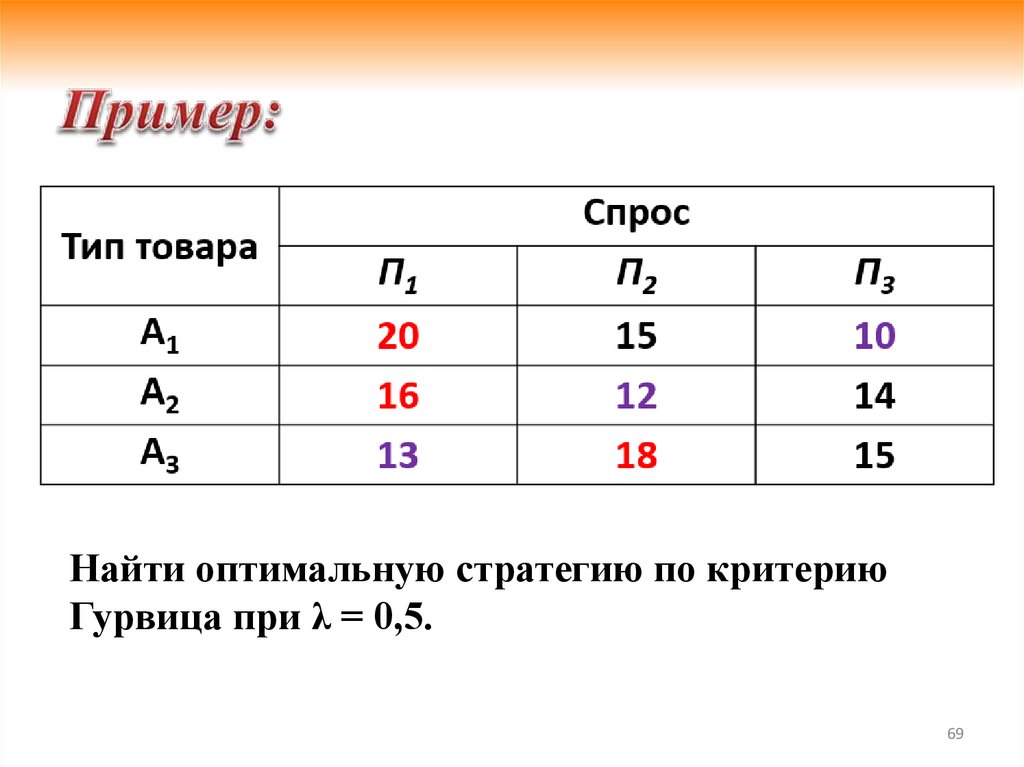
Рекомендация по оформлению:69.
Найти оптимальную стратегию по критериюГурвица при λ = 0,5.
69
70.
7071.
ЗамечанияПри использовании данного критерия ЛПР фактически
учитывает только информацию о наилучшем и
наихудшем результатах при выборе каждой из
стратегий. Остальные элементы платежной матрицы
никак не используются. Таким образом, часть
информации при принятии решения игнорируется.
Применение критерия оправдано, если ситуация, в
которой он используется, характеризуется следующими
обстоятельствами:
- о вероятностях появления состояний природы Пj
ничего не известно;
- фактически достаточно знать влияние наилучшего и
наихудшего из них;
- решение принимается один раз и допускается
некоторый риск.
72.
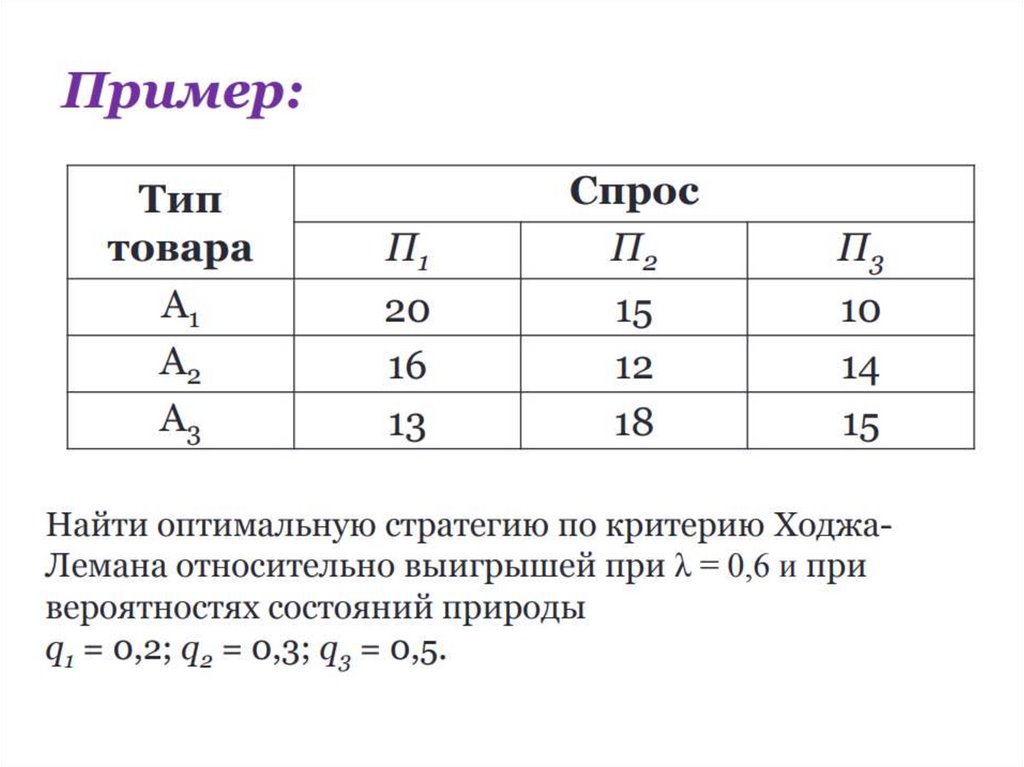
2. Критерий Ходжа-Лемана73.
Оптимальная стратегия по критерию ХоджаЛемана определяется как та, на которойреализуется максимум выражения:
Замечание. Иногда, если вероятности состояний природы не известны,
используют предположение о равновероятных состояниях, как в критерии
Лапласа. Риск при этом увеличивается.
73
74.
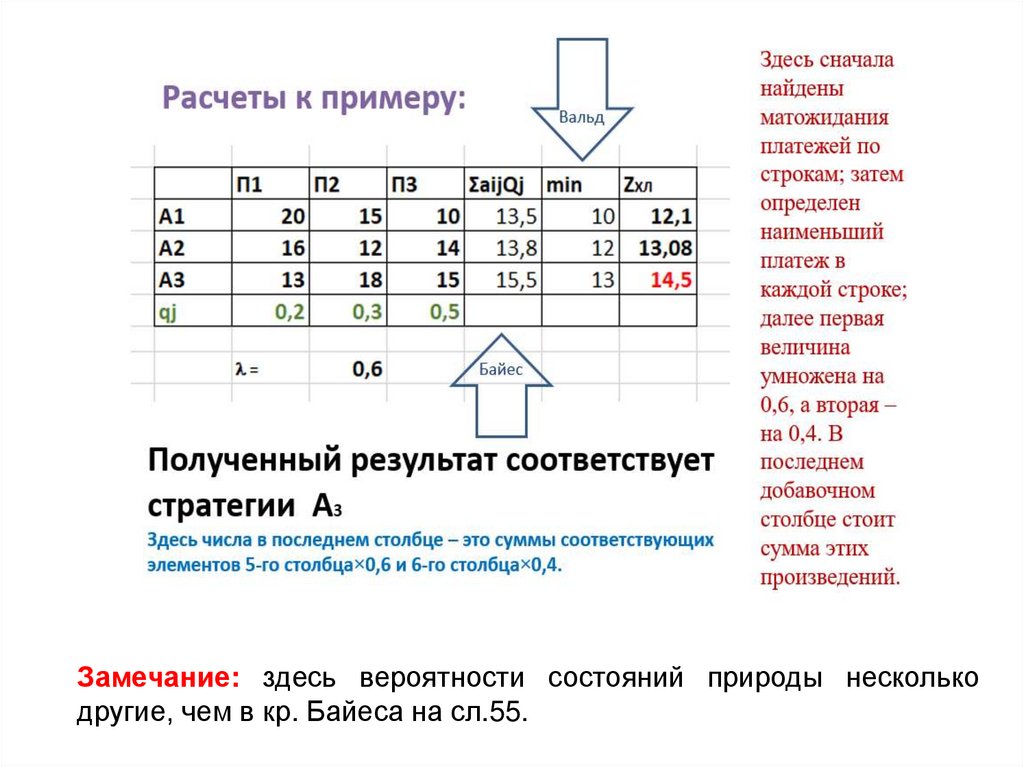
7475.
76.
Замечание: здесь вероятности состояний природы несколькодругие, чем в кр. Байеса на сл.55.
77.
Он применяется для задач принятия решений вусловиях риска, для решения задач выбора стратегии с
целью оптимизации величины потерь или издержек.
Такие задачи довольно часто встречаются в
хозяйственной практике при оценке экономических,
логистических затрат.
Предполагается, как и в критерии Ходжа-Лемана, что
ЛПР обладает дополнительной информацией о
вероятностях состояний природы.
Юрий Борисович Гермейер (18 июля 1918-24 июня 1975) советский учёный, специалист в области прикладной математики,
исследования операций и теории игр. Основатель кафедры
исследования операций на факультете вычислительной математики
и кибернетики МГУ.
77
78.
3.1. Понятие игры с природой78
79.
Пусть вероятности состояний спроса те же, что в предыдущемслучае:
79
80.
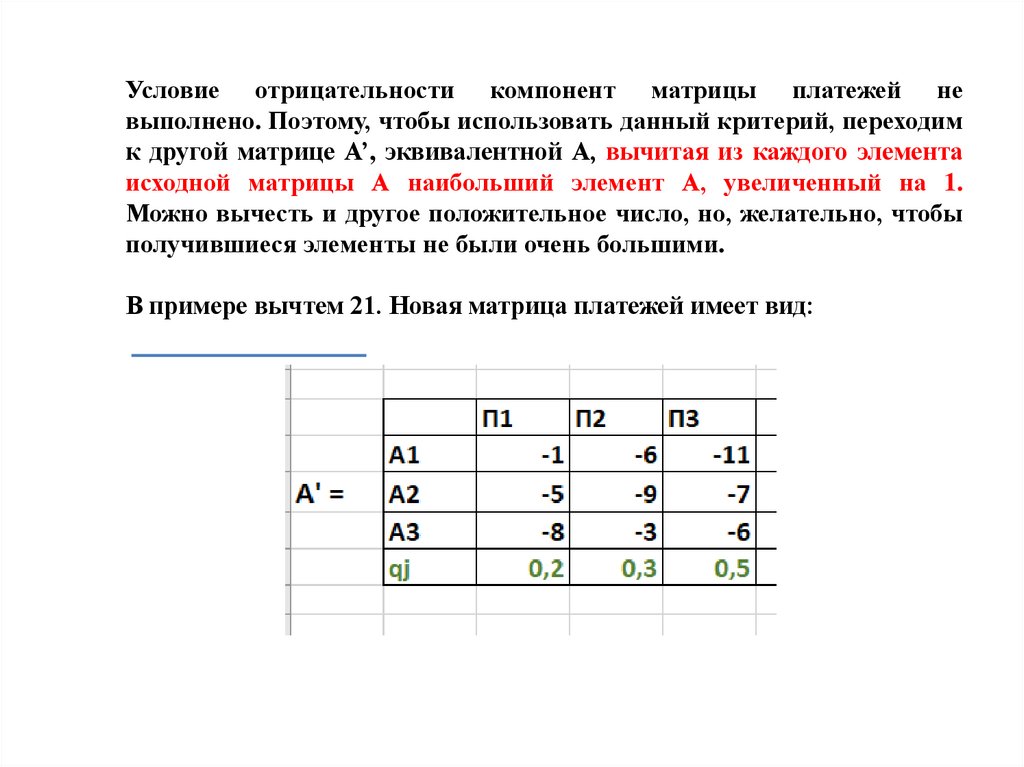
Условие отрицательности компонент матрицы платежей невыполнено. Поэтому, чтобы использовать данный критерий, переходим
к другой матрице А’, эквивалентной А, вычитая из каждого элемента
исходной матрицы А наибольший элемент А, увеличенный на 1.
Можно вычесть и другое положительное число, но, желательно, чтобы
получившиеся элементы не были очень большими.
В примере вычтем 21. Новая матрица платежей имеет вид:
81.
Расчеты к примеру:Наиболь
шее из
минима
льных
произве
дений с
учетом
вероятн
ости
спроса
Полученный результат соответствует
стратегии А3
82.
Замечание.Критерий Гермейера в чем-то похож и на критерий Вальда и на критерий
Байеса. На первый – в том, что ЛПР также действует по принципу «лучшее
из худших», но объективнее оценивает результат. Сходство со вторым - в
необходимости знать вероятности состояний природы.
Условия применимости :
- элементы платежной матрицы ≤ 0;
- вероятности появления состояний Пj известны;
- с появлением тех или иных состояний, отдельно или в комплексе,
необходимо считаться;
- допускается некоторый риск;
- решение может реализоваться один или много раз.
Если функция распределения известна не очень надежно, а число
реализаций ситуации мало, то, следуя критерию Геймейера, получают,
вообще говоря, неоправданно большой риск. Таким образом, здесь
остается некоторая свобода для субъективных действий.
83.
4. Критерий произведенийКритерий произведений основан на максимизации величины
Матрица решений дополняется новым столбцом,
содержащим произведения всех компонент каждой строки
при условии, что все aij > 0. Выбираются те варианты, в
строках которых находятся наибольшие значения этого
столбца.
83
84.
Применениеэтого
критерия
обусловлено
следующими обстоятельствами:
1) вероятности появления состояний природы
неизвестны;
2) с появлением каждого из состояний необходимо
считаться;
3) допускается малое число реализаций решения;
4) возможен некоторый риск.
84
85.
Если условие положительности компонент платежной матрицы нарушено,то следует выполнять некоторый сдвиг aij + a с некоторой константой a > 0.
Если же никакая константа не может быть признана имеющей смысл, то
критерий произведений неприменим.
Следует также отметить, что, если среди элементов некоторой строки
платежной матрицы имеется элемент, положительный, но очень близкий к
нулю, а остальные элементы не сильно отличаются друг от друга,
использование критерия произведений наверняка приведет к «невыбору»
(обесцениванию) соответствующей стратегии. Таким образом, снижается
риск получить решение, для которого существует результат в виде почти
нулевой выгоды при одном из состояний природы.
85
86.
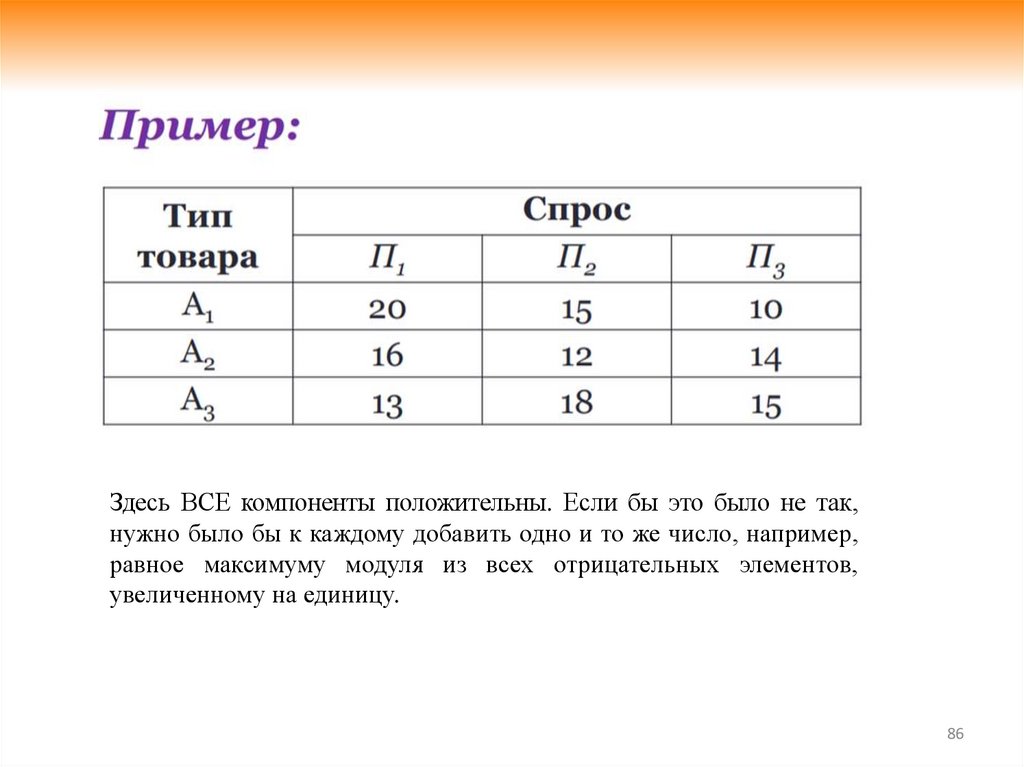
Здесь ВСЕ компоненты положительны. Если бы это было не так,нужно было бы к каждому добавить одно и то же число, например,
равное максимуму модуля из всех отрицательных элементов,
увеличенному на единицу.
86
87.
Расчеты к примеру:Наибольшее
из
произведен
ий
элементов
строк
Полученный результат соответствует
стратегии А3
87
88.
Замечание.Выбор
оптимального
решения
согласно
данному
критерию
оказывается менее пессимистическим, чем,
например,
выбор в соответствии с максиминным
критерием
Вальда.
В
результате
применения
критерия
происходит некоторое выравнивание между
большими и малыми
значениями выигрышей aij, и,
устанавливая оптимальный вариант решения, мы можем
при фиксированных состояниях Пj получить большую
выгоду, чем при использовании критерия гарантированного
результата,
но
при
этом
должна
учитываться
возможность появления и худших результатов. Следует
отметить, что при использовании этого критерия ни число
реализаций, ни информация о распределении вероятностей
не принимаются во внимание.
89.
3.2. Принятие решений в условиях неопределенностиОбщий вывод по четырем
критериям:
Стратегия
А3 является безоговорочным
лидером и рекомендуется к окончательному
выбору.
89




















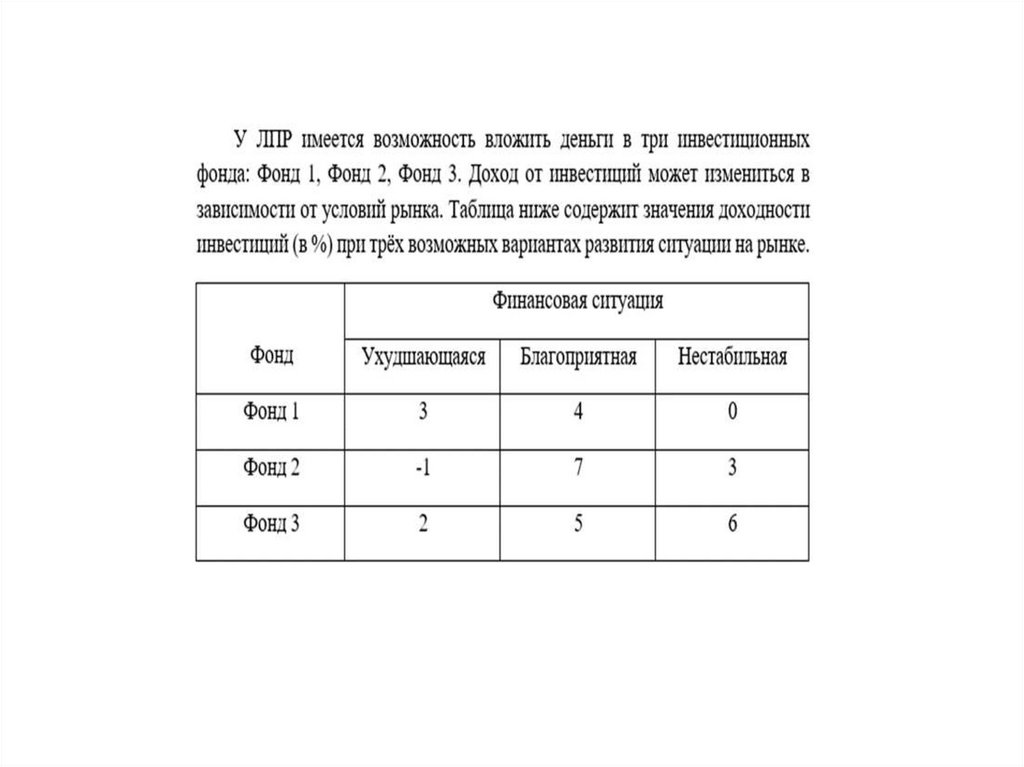

























































 Математика
Математика