Похожие презентации:
Алгоритмы на графах. Часть 3
1.
АЛГОРИТМЫ НА ГРАФАХ ЧАСТЬ 3Циклы
Компоненты связности
Топологическая сортировка
2.
• Поиск в глубину и его приложения• Пометки времени
• Компоненты связности
• Топологическая сортировка
• Эйлеров цикл
• Гамильтонов цикл
3.
Поиск в глубину• Согласно этому алгоритму обход вершин графа осуществляется по
следующему правилу.
• Начиная с некоторой вершины, мы идем по ребрам графа, пока не упремся в
тупик. Вершина называется тупиком, если в ней нет исходящих ребер,
ведущих в непосещенные вершины.
• После попадания в тупик мы возвращаемся назад вдоль пройденного пути,
пока не обнаружим вершину, у которой есть исходящие ребра, ведущие в
непосещенные вершины, и из нее идем по одному из таких ребер.
• Процесс кончается, когда мы возвращаемся в начальную вершину, а все
соседние вершины уже оказались посещенными.
• Если после этого остаются непосещенные вершины, то повторяем поиск из
одной из них в соответствии с вышеописанным алгоритмом. Так делаем до
тех пор, пока не обнаружим все вершины графа.
4.
Поиск в глубину• Переходя в вершину U из вершины V по ребру (V, U), мы
запоминаем предшественника U при обходе в глубину: p[U] = V
• Для вершин, у которых предшественников нет, положим
p[U] = −1. Таким образом, получается дерево поиска в глубину
• Если поиск повторяется из нескольких вершин, то получается
несколько деревьев, образующих лес поиска в глубину
• Лес поиска в глубину состоит из всех вершин исходного графа и
ребер, по которым эти вершины впервые достигнуты
5.
Поиск в глубину• Для наглядности будем считать, что в процессе работы алгоритма
вершины графа могут быть белыми, серыми и черными
• Изначально все вершины помечены белым цветом:
color[V] = white
• Впервые обнаружив вершину V, мы красим ее серым цветом:
color[V] = grey
• По окончании обработки всех исходящих ребер красим вершину V в
черный цвет: color[V] = black
6.
Поиск в глубину• Для каждой вершины в процессе поиска в глубину полезно запоминать
еще два параметра:
• в d[v] будем записывать «время» первого попадания в вершину;
• в f [v] —«время» окончания обработки всех исходящих из v ребер.
• При этом d[v] и f [v] представляют собой целые числа из диапазона от 1 до 2|V|, где
|V|—число вершин графа.
• Вершина v будет белой до момента d[v] , серой между d[v] и f [v] , черной
после f [v] .
7.
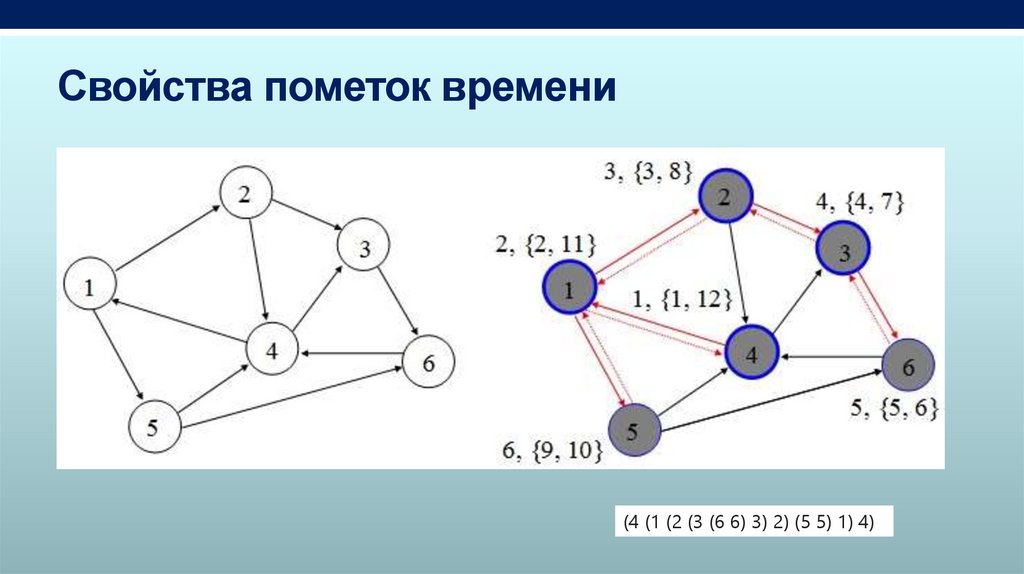
Свойства пометок времени• Время обнаружения и время окончания обработки образуют правильную
скобочную структуру.
• Таким образом, для любой вершины u из W(v) верно: d[v] < d[u] < f [u] < f
[v] , что соответствует выражению (v... (u...u) ...v). (Доказательство – по
индукции).
8.
Свойства пометок времени• При поиске в глубину как в ориентированном, так и в неориентированном
графе для любых двух вершин u и v выполняется ровно одно из трех
утверждений:
1. отрезки [d[u] , f [u] ] и [d[v] , f [v] ] не пересекаются;
2. отрезок [d[u] , f [u] ] целиком содержится внутри отрезка [d[v] , f [v] ] , и u потомок v в дереве поиска в глубину;
3. отрезок [d[v] , f [v] ] целиком содержится внутри отрезка [d[u] , f [u] ] , и v потомок u в дереве поиска в глубину.
• Эти утверждения позволяют быстро определять взаимное расположение
вершин в лесу поиска в глубину.
Теорема про белый путь. Вершина v является потомком вершины u в
лесу поиска в глубину тогда и только тогда, когда в момент d[u]
обнаружения вершины u существует путь из u в v, состоящий только
из белых вершин.
9.
Свойства пометок времени(4 (1 (2 (3 (6 6) 3) 2) (5 5) 1) 4)
10.
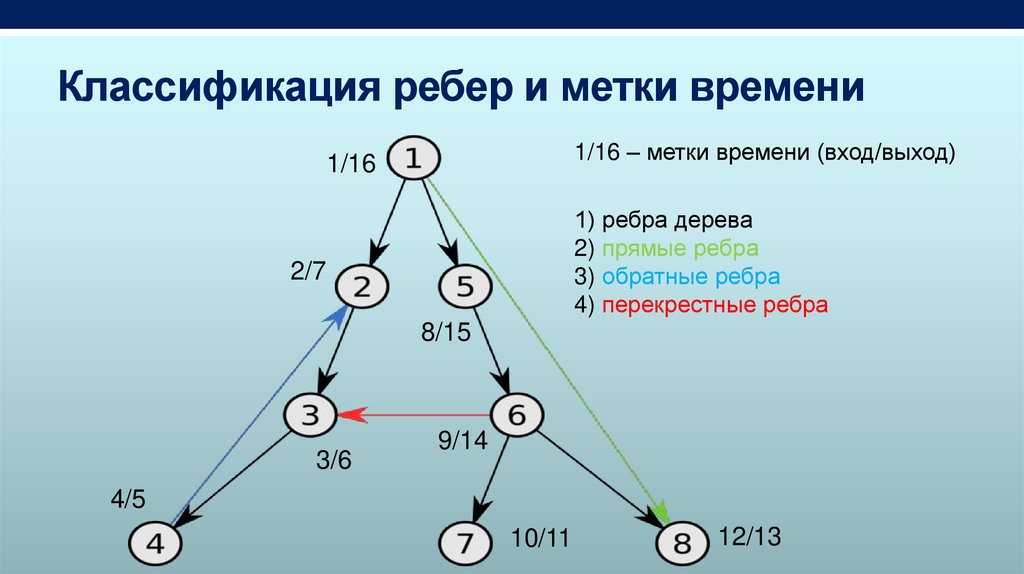
Классификация реберРебра ориентированного графа делятся на несколько категорий в
зависимости от их роли при поиске в глубину.
1. Ребра деревьев - это ребра, входящие в лес поиска в глубину.
2. Прямые ребра - это ребра, соединяющие вершину с ее потомком, но не
входящие в лес поиска в глубину.
3. Обратные ребра - это ребра, соединяющие вершину c ее предком в
дереве поиска в глубину (ребра-циклы, возможные в ориентированных
графах, считаются обратными ребрами).
4. Перекрестные ребра - все остальные ребра графа. Они могут
соединять две вершины из одного дерева поиска в глубину, если ни
одна их этих вершин не является предком другой, или же вершины из
разных деревьев.
11.
Классификация ребер и метки времени1/16 – метки времени (вход/выход)
1/16
1) ребра дерева
2) прямые ребра
3) обратные ребра
4) перекрестные ребра
2/7
8/15
3/6
9/14
4/5
10/11
12/13
12.
Классификация ребер• Тип ребра (V, U) можно определить по цвету вершины U в
момент, когда ребро исследуется в первый раз:
белый цвет означает ребро дерева ((V, U) войдет в лес поиска в
глубину)
серый (U является предком V) – обратное ребро
черный ( ни одна из них не является предком другой) – прямое или
перекрестное ребро
Ориентированный граф не имеет циклов тогда и
только тогда, когда поиск в глубину не находит в нем
обратных ребер
13.
Классификация ребер• Тип ребра (v, u) можно определить по пометкам времени
a) ребром дерева или прямым ребром тогда и только тогда, когда
d[u] < d[v] < f[v] < f[u]
b) обратным ребром тогда и только тогда, когда
d[v] < d[u] < f[u] < f[v]
c) поперечным ребром тогда и только тогда, когда
d[v] < f[v] < d[u] < f[u]
Теорема. О классификации ребер в неориентированном графе. При
поиске в глубину в неориентированном графе произвольное
ребро является или ребром дерева, или обратным. Прямых и
перекрестных ребер не существует.
14.
Поиск цикла в неориентированном графе• Также будем «красить» вершины в различные цвета (1 (белый) — мы еще
не посещали вершину, 2 (серый) — посетили вершину и
зациклились, 3 (черный) — посетили вершину и вышли из неё).
• В векторе M будем хранить сам граф.
• Для проверки на цикличность воспользуемся векторами visited и colours:
• в первом будем отмечать посещали ли мы вершину ранее или нет,
• во втором же изначально будут хранится только 1 (белые) вершины, далее, по мере
поиска, они будут приобретать другие цвета.
• Если мы захотим посетить 2 (серую) вершину, то это будет означать, что
мы отыскали цикл в этой вершине.
• Осталось лишь вывести его на экран. Для этого ищем вершины, цвет
которых 2 (серый), для первой встретившейся вершины, в которой есть
цикл, выведем вторую вершину.
15.
Поиск цикла в неориентированном графеint t = 0;
for (int i = 0; i < n; i++) {
if (dfs(i)) t = 1;
}
if (t == 0)
cout << "NO";
else {
cout << "YES" << endl;
vector <int> iscyclic;
for (int i = 0; i < colours.size(); i++) {
if (colours[i] == 2) iscyclic.push_back(i);
}
cyclic (iscyclic[0]);
for (int i = 1; i < cyclicnodes.size(); i++)
cout << cyclicnodes[i] + 1 << " ";
}
16.
Поиск цикла в неориентированном графе// рекурсивный поиск в глубину для каждой вершины, так же помечаем каждую вершину одним из трех
цветов
bool dfs (int v) {
colours[v] = 2;
visited[v]++;
for (int i = 0; i < M[v].size(); i++) {
if (colours[M[v][i]] != 3 and visited[M[v][i]] != 2) {
if (colours[M[v][i]] == 1) {
if (dfs(M[v][i])) return true;
}
else {
if (colours[M[v][i]] == 2) return true;
}
}
if (colours[v] == 3) return false;
if (visited[v] == 2) return false;
}
colours[v] = 3;
return false;
}
17.
Поиск цикла в неориентированном графе// поиск цикличных вершин
void cyclic (int v) {
for (int i = 0; i < M[v].size(); i++) {
cyclicnodes.push_back(M[v][i]);
if (cyclicnodes[0] == cyclicnodes[cyclicnodes.size() - 1] and cyclicnodes.size() > 1)
break;
cyclic (M[v][i]);
}
}
18.
Топологическая сортировка• Пусть имеется ориентированный граф G без циклов. Задача о
топологической сортировке этого графа состоит в том, чтобы указать
такой порядок вершин, при котором ребра графа ведут только из вершин
с меньшим номером к вершинам с большим номером.
• Если в графе есть циклы, то такого порядка не существует.
• Можно переформулировать задачу о топологической сортировке
следующим образом: расположить вершины графа на горизонтальной
прямой так, чтобы все ребра графа шли слева направо.
19.
Топологическая сортировка• Применяется при создании параллельных алгоритмов, когда по
некоторому описанию алгоритма нужно составить граф зависимостей его
операций и, отсортировав его топологически, определить, какие из
операций являются независимыми и могут выполняться параллельно
(одновременно).
• Примером использования топологической сортировки может служить
создание карты сайта, где имеет место древовидная система разделов.
• Также топологическая сортировка применяется при обработке исходного
кода программы в некоторых компиляторах и IDE, где строится граф
зависимостей между сущностями, после чего они инициализируются в
нужном порядке, либо выдается ошибка о циклической зависимости.
• Также с помощью топологической сортировки можно найти гамильтонов
путь в ациклическом графе.
20.
Топологическая сортировкаПрименим поиск в глубину к нашему графу.
• Завершая обработку каждой вершины (делая ее черной), заносим ее в
начало списка.
• Если вдруг вошли в серую вершину - найден цикл, топологическая
сортировка невозможна.
• По окончании обработки всех вершин полученный список будет
содержать топологическую сортировку данного графа.
• Таким образом, искомая топологическая сортировка — это сортировка в
порядке убывания времён выхода.
• Так как в результирующий список должны попасть все n вершин нашего
графа, то реализовать его можно на обычном массиве, записывая в него
элементы списка начиная с n-го места в массиве и заканчивая первым.
21.
Топологическая сортировка(1)
(4)
(5)
(3)
(2)
Визуализация:
https://www.cs.usfca.edu/~galles/visualization/TopoSortDFS.html
22.
Топологическая сортировкаvoid dfs (int v) {
used[v] = true;
for (size_t i=0; i<g[v].size(); ++i) {
int to = g[v][i];
if (!used[to])
dfs (to);
}
ans.push_back (v);
}
void topological_sort() {
for (int i=0; i<n; ++i)
used[i] = false;
ans.clear();
for (int i=0; i<n; ++i)
if (!used[i])
dfs (i);
reverse (ans.begin(), ans.end());
}
23.
Эйлеров цикл• Эйлеровым путем (англ. Eulerian path) в графе называется путь,
который проходит по каждому ребру, причем ровно один раз.
• Эйлеров цикл (англ. Eulerian cycle) — замкнутый эйлеров путь.
• Граф называется эйлеровым (англ. Eulerian graph), если он содержит
эйлеров цикл.
• Граф называется полуэйлеровым, если он содержит эйлеров путь, но не
содержит эйлеров цикл.
• Если в графе существует более одной компоненты связности с ребрами,
то очевидно, что нельзя пройти по их ребрам одним путем
24.
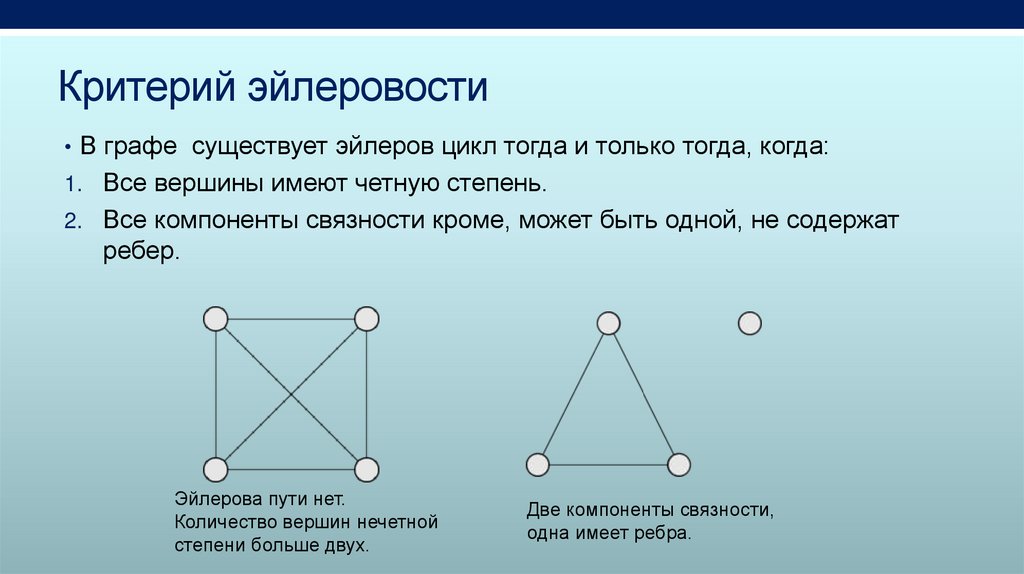
Критерий эйлеровости• В графе существует эйлеров цикл тогда и только тогда, когда:
1. Все вершины имеют четную степень.
2. Все компоненты связности кроме, может быть одной, не содержат
ребер.
Эйлерова пути нет.
Количество вершин нечетной
степени больше двух.
Две компоненты связности,
одна имеет ребра.
25.
Эйлеров цикл• Перед запуском алгоритма необходимо проверить граф на эйлеровость.
• Чтобы построить Эйлеров путь, нужно запустить алгоритм из вершины с
нечетной степенью.
• Используется просмотр графа методом поиска в глубину, при этом ребра
удаляются.
• Порядок просмотра (номера вершин) запоминается.
• При обнаружении вершины, из которой не выходят ребра, мы их удалили, ее
номер записывается в стек, и просмотр продолжается от предыдущей вершины.
• Обнаружение вершин с нулевым числом ребер говорит о том, что найден цикл.
• Его можно удалить, четность вершин (количество выходящих ребер ) при этом
не изменится.
• Процесс продолжается до тех пор, пока есть ребра.
• В стеке после этого будут записаны номера вершин графа в порядке,
соответствующем эйлерову циклу.
26.
Эйлеров циклprocedure FindEulerPath (V)
1. перебрать все рёбра, выходящие из вершины V;
каждое такое ребро удаляем из графа, и
вызываем FindEulerPath из второго конца этого ребра;
2. добавляем вершину V в ответ.
Сложность этого алгоритма, очевидно, является линейной относительно
числа рёбер.
27.
Эйлеров циклvoid search_euler (int v, vector < vector < int > > &D, vector < int > &c)
{
for (int i = 0; i < D[v].size (); ++ i)
if (D[v][i]) {
/// если ребро есть, то проходим по нему
D[v][i] = 0;
D[i][v] = 0;
search_euler (i, D, c);
}
c.push_back (v);
}
28.
Эйлеров цикл2
7
2
7
6
6
1
1
5
5
3
4
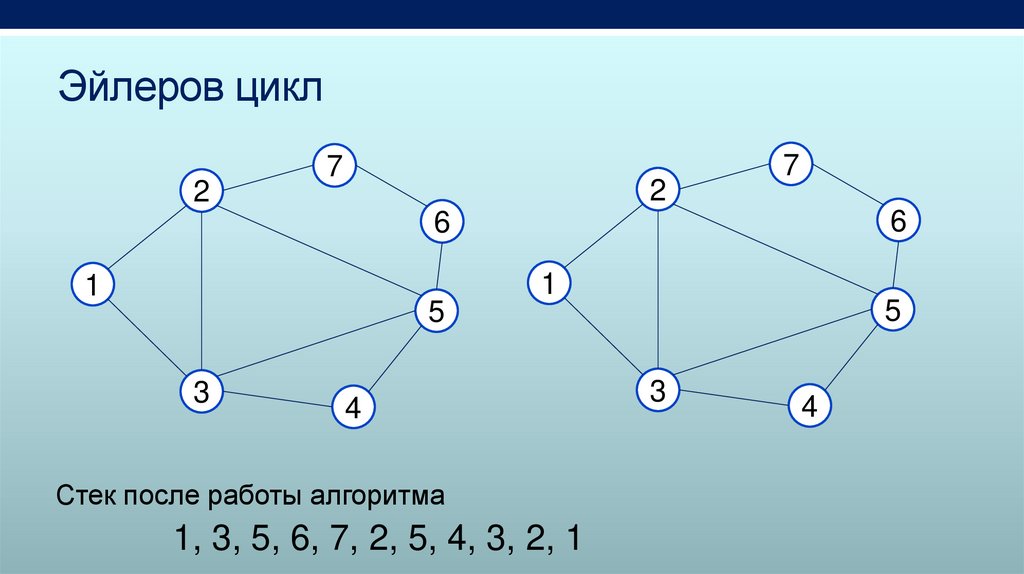
Стек после работы алгоритма
1, 3, 5, 6, 7, 2, 5, 4, 3, 2, 1
3
4
29.
Эйлеров цикл. Время работы• Если реализовать поиск ребер инцидентных вершине и удаление ребер
за O(1), то алгоритм будет работать за O(E).
• Чтобы реализовать поиск за O(1):
• для хранения графа следует использовать списки смежных вершин;
• для удаления достаточно добавить всем ребрам свойство deleted
бинарного типа.
• Ухудшить алгоритм может лишь процедура удаления ребра из графа,
которая встречается почти в каждой итерации.
• на поиски удаляемого ребра затрачивается время 2*O(n), где n количество вершин графа.
• Из приведенных рассуждений можно сделать вывод, что общая
сложность алгоритма есть O(VE).
30.
Деревья Эйлерова обхода• Для динамически изменяющегося дерева выполнить следующие
запросы:
• link(u,w) — добавить ребро (u,w) (при условии, что вершины u и w
принадлежат разным деревьям),
• cut(u,w) — разрезать ребро (u,w) (при условии, что ребро (u,w)
принадлежит дереву),
• isConnected(u,w) — определить принадлежат ли вершины u и w одной
компоненте связности.
31.
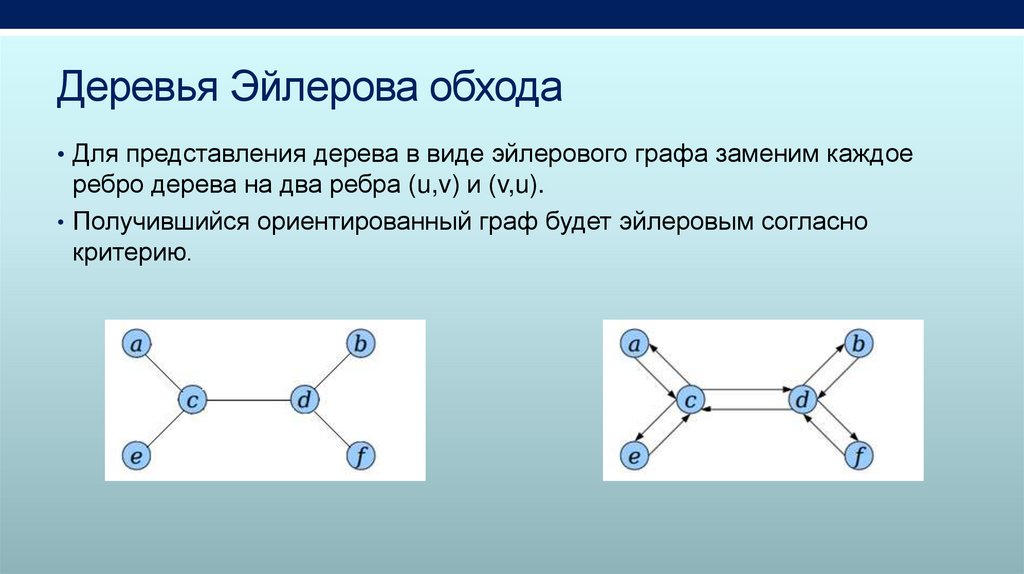
Деревья Эйлерова обхода• Для представления дерева в виде эйлерового графа заменим каждое
ребро дерева на два ребра (u,v) и (v,u).
• Получившийся ориентированный граф будет эйлеровым согласно
критерию.
32.
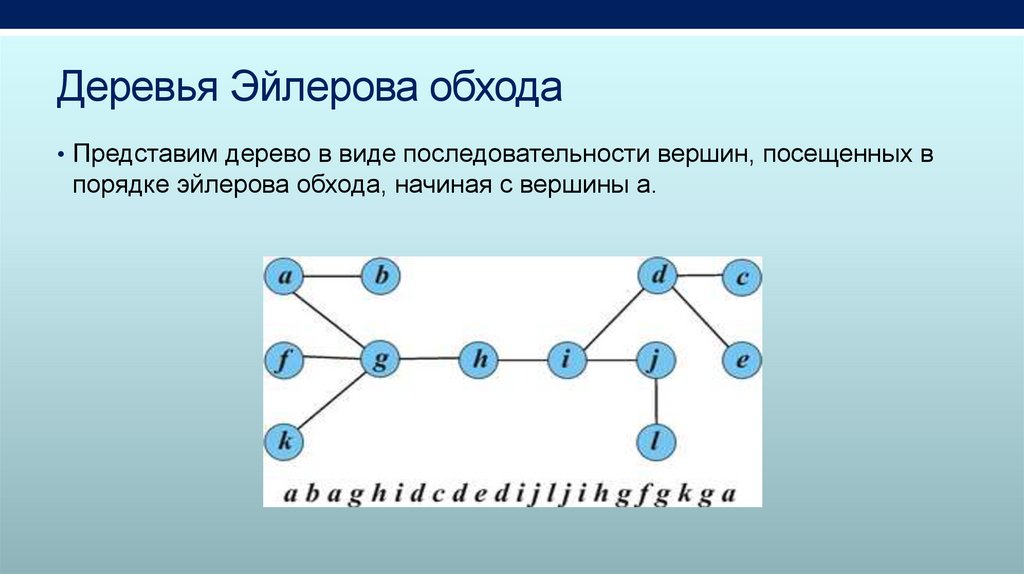
Деревья Эйлерова обхода• Представим дерево в виде последовательности вершин, посещенных в
порядке эйлерова обхода, начиная с вершины a.
33.
Деревья Эйлерова обхода• https://neerc.ifmo.ru/wiki/index.php?title=%D0%94%D0%B5%D1%80%D0%B
5%D0%B2%D1%8C%D1%8F_%D0%AD%D0%B9%D0%BB%D0%B5%D1%
80%D0%BE%D0%B2%D0%B0_%D0%BE%D0%B1%D1%85%D0%BE%D0
%B4%D0%B0
• http://codeforces.com/blog/entry/18369?locale=ru
34.
Гамильтоновы графы• Гамильтоновым путём (англ. Hamiltonian path) называется простой путь,
проходящий через каждую вершину графа ровно один раз.
• Гамильтоновым циклом (англ. Hamiltonian cycle) называют замкнутый
гамильтонов путь.
• Граф называется полугамильтоновым (англ. Semihamiltonian graph),
если он содержит гамильтонов путь.
• Граф называется гамильтоновым (англ. Hamiltonian graph), если он
содержит гамильтонов цикл.
35.
Достаточные условия гамильтоновости графа• Если






























 Математика
Математика








