Расчёт показателей балансовой надёжности для ЭЭС с сильными связями

1.

РАСЧЁТ ПОКАЗАТЕЛЕЙ БАЛАНСОВОЙ НАДЁЖНОСТИ ДЛЯ
ЭЭС С СИЛЬНЫМИ СВЯЗЯМИ
Выпускная квалификационная работа по направлению
13.03.02 – Электроэнергетика и электротехника
Студент:
Белоусов Александр Максимович
Руководитель:
Губин Павел Юрьевич
Екатеринбург
2023

2.

Балансовая надёжность
Балансовая надежность (БН) определяется как способность ЭЭС обеспечивать совокупную потребность в
электрической мощности и энергии потребителей с учетом ограничений в виде плановых и неплановых
отключений элементов ЭЭС и ограничений на поставку энергоресурсов и определяет обеспечение спроса на
электроэнергию и мощность с учетом характеристик и режимов работы элементов ЭЭС.
Одними из главных показателей БН являются:
Вероятность безотказной работы ЭЭС;
Математическое ожидание недоотпуска электроэнергии потребителям;
2

3.

Цели и задачи работы
Цель работы: Разработать программу, которая будет выполнять вычисление МО и
вероятность дефицита мощности.
Задачи работы:
1. Выполнить анализ методов оценки ПБН
2. Реализовать расчёт МО и вероятности дефицита
варианта ЭЭС в Microsoft excel
3. Реализовать расчёт МО и вероятности дефицита
варианта ЭЭС в Visual Studio
4. Сравнить полученные результаты
5. Сделать вывод об эффективности каждого из методов
3

4.

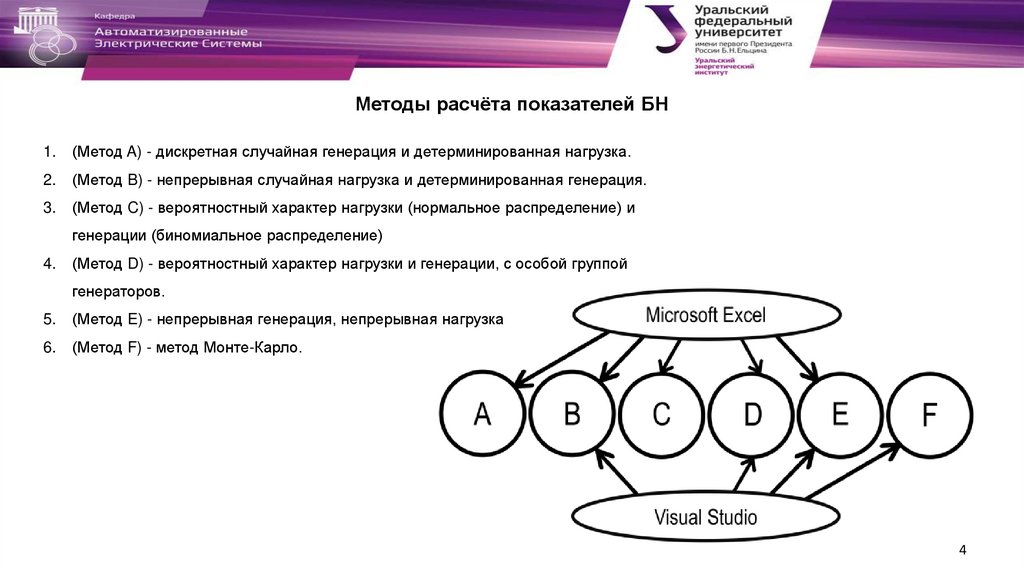
Методы расчёта показателей БН
1.
(Метод A) - дискретная случайная генерация и детерминированная нагрузка.
2.
(Метод B) - непрерывная случайная нагрузка и детерминированная генерация.
3.
(Метод C) - вероятностный характер нагрузки (нормальное распределение) и
генерации (биномиальное распределение)
4.
(Метод D) - вероятностный характер нагрузки и генерации, с особой группой
генераторов.
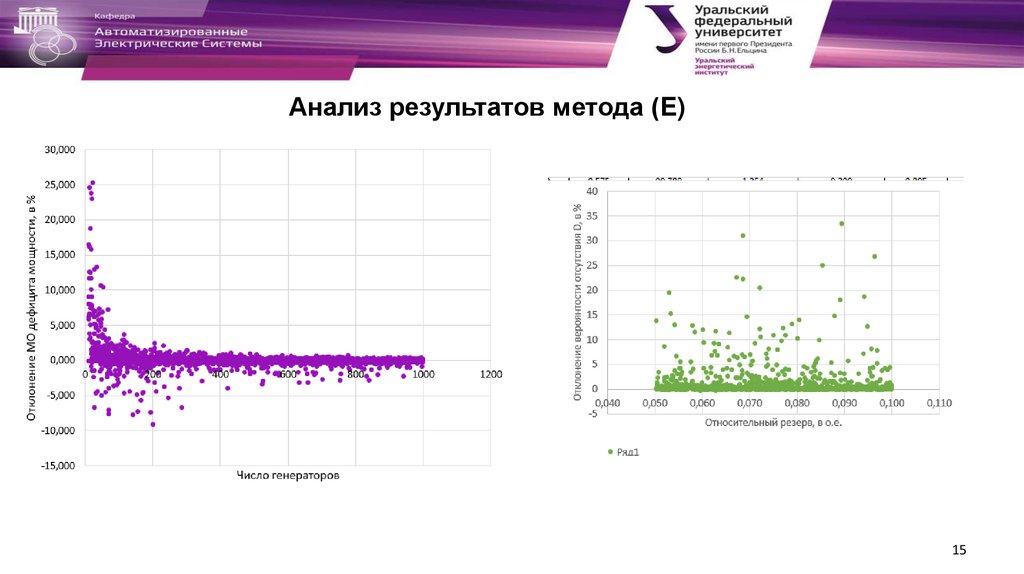
5.
(Метод E) - непрерывная генерация, непрерывная нагрузка
6.
(Метод F) - метод Монте-Карло.
4

5.

Метод (А) - дискретная случайная
генерация и детерминированная нагрузка
Случайное число k работоспособных агрегатов в группе из n энергоблоков описывается
биномиальным распределением
B k, n, q = Cnk ⋅ pk ⋅ qn−k ,
где p – вероятность безотказной работы генератора, Cnk - число сочетаний из n элементов по k
Вероятность дефицита мощности можно рассчитать в соответствии со следующей формулой
n
P(D) = ෍ B k, n, q ⋅ η
k=0
Математическое ожидание (МО) дефицита мощности можно найти как
n
М D = ෍ B k, n, q ⋅ η ⋅ L − Gk ,
k=0
где η – индикатор дефицитного состояния, Gk - располагаемая мощность генерации.
5

6.

Метод (B) - непрерывная случайная нагрузка и
детерминированная генерация
Нагрузка распределяется в соответствии с функцией распределения FL
L~N(mL , σL )
Тогда вероятность дефицита мощности
P D = Ƿ L > G = ℱL G = 1 − FL G ,
где FL G - функция распределения нагрузки
МО дефицита мощности
∞
∞
М(D) = න (x − G) ⋅ dFL (x) = න x ⋅ dFL (x) − G ⋅ (1 − FL (G))
В свою очередь
G
G
∞
න x ⋅ dFL (x) = mL ⋅ ℱL (G) + σL 2 ⋅ fL (G)
И в результате получаем
G
М D = mL − G ⋅ ℱL G + σL 2 ⋅ fL G ,
где mL - это МО нагрузки, σL - СКО нагрузки
6

7.

Метод (С)- вероятностный характер нагрузки и
биноминальное распределение генерации
Вероятность дефицита мощности можно найти как
n
P D = ෍ B k, n, q ⋅ ℱL (Gk , mL , σL )
k=0
где – k число отключенных блоков; B k, n, q – вероятность биномиального
распределения; Gk = k Pбл – располагаемая мощность. МО дефицита мощности
n
M D = ෍ B k, n, q ⋅ ηk ⋅ Mk (D)
k=0
где Mk(D) – МО дефицита мощности, соответствующее Gk :
Mk (D) = (mL − Gk ) ⋅ ℱL (Gk ) + σL 2 ⋅ fL (Gk )
7

8.

Метод (D) - вероятностный характер нагрузки и
генерации, с особой группой генераторов
Как и ранее будет анализироваться небаланс мощности