Расчёт показателей надёжности схем электроснабжения (тема № 3)

1.

ТЕМА №3 РАСЧЁТ ПОКАЗАТЕЛЕЙ НАДЁЖНОСТИ СХЕМ
ЭЛЕКТРОСНАБЖЕНИЯ
3.1 Надёжность структур с последовательным соединением
элементов.
3.2 Надёжность структур с параллельным соединением
элементов.
3.3 Надёжность структур со смешанным соединением
элементов.
3.4 Метод минимальных сечений для расчёта надёжности
сложных структур.

2.

3.1 Надёжность структур с последовательным
соединением элементов
Последовательным соединением называется такая структура,
отказ которой наступает при выходе из строя хотя бы одного
элемента, т. е. последовательная структура работоспособна, если
все её элементы работоспособны.

3.

1. Вероятность безотказной работы последовательной структуры
n
Pс ( t ) P(
1 t ) P2 ( t ) ... Pn ( t ) P(
i t ). (3.1)
i 1
2. Вероятность отказа последовательной структуры
n
n
Qс ( t ) 1 Pс ( t ) 1 P(
i t ) 1 ( 1 Qi ( t )).
i 1
i 1
(3.2)

4.

3. Параметр потока отказов структуры:
n
ωс ωi .
(3.3)
i 1
4. Среднее время безотказной работы с учётом (2.34)
1
Tс .
ωс
(3.4)
5. Среднее время восстановления структуры:
1 n
Т Вс
ωiТ Вi .
ωс i 1
(3.5)

5.

3.2 Надёжность структур с параллельным
соединением элементов
Параллельным соединением называется структура, отказ
которой наступает при отказе всех элементов, входящих в
структуру.

6.

1. Вероятность отказа параллельной структуры
n
Qс ( t ) Q1( t ) Q2 ( t ) ... Qn ( t ) Q j ( t ). (3.11)
j 1
2. Вероятность безотказной работы параллельной структуры
n
n
j 1
j 1
Pс ( t ) 1 Qс ( t ) 1 Q j ( t ) 1 ( 1 Pj ( t )).(3.12)

7.

1
(max)
T(min) ω
TВ(max) .
(3.13)
Для m параллельно соединенных элементов
m
m
(m)
1
ωс ω j TВj TВj ;
j 1
j 1
(m)
Вc
T
-1
-1
T Вj .
j 1
m
(3.14)
(3.15)

8.

Для структуры, состоящей из двух параллельно
соединенных элементов 1 и 2, параметр потока отказов
ω
ω1 ω2 TВ1 TВ2
(3.16)
(2)
c
TВ1 TВ2
ω ω
,
(3.17)
(2)
c
или
ω
1
2
8760
среднее время восстановления
(2)
Вc
T
TВ1 TВ2
.
TВ1 TВ2
(3.18)

9.

3.3 Метод минимальных сечений для расчета надёжности
сложных структур
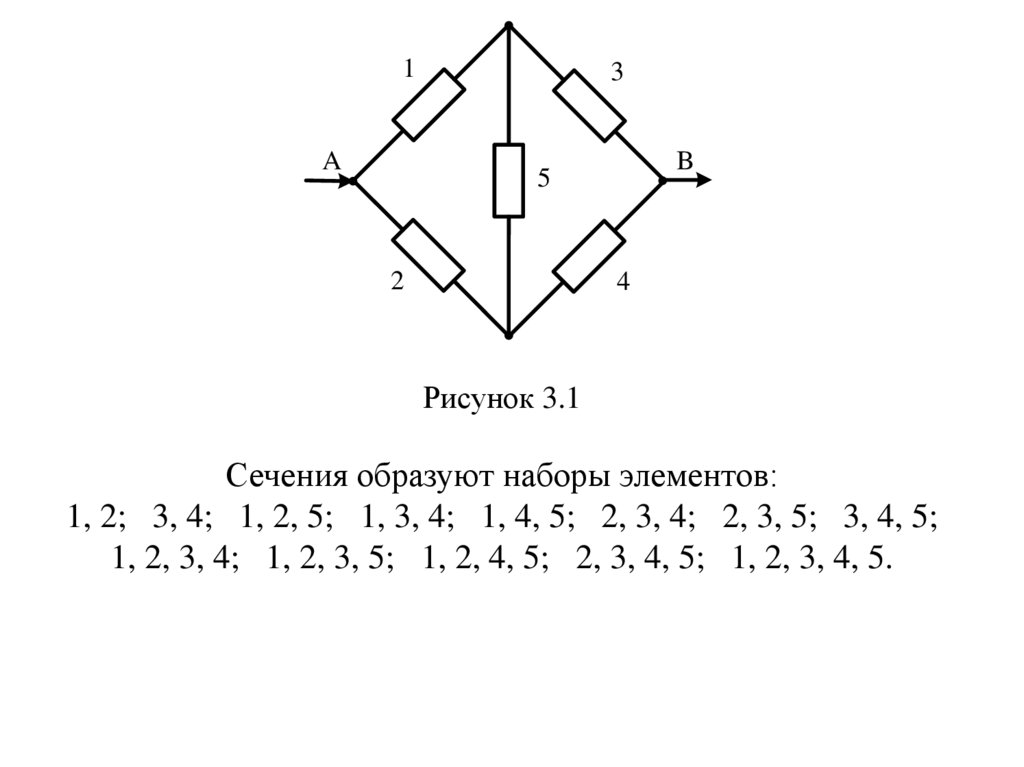
Существуют и более сложные структуры, например, мостиковая
схема (рис. 3.1). В этой структуре элементы соединены таким
образом, что её дальнейшее упрощение невозможно.
Набор элементов, отказ которых приводит к отказу структуры
(т.е. разрыву всех связей между входом и выходом) в теории
надёжности называется сечением.
Если выявить все сечения, содержащиеся в исследуемой
структуре, и определить их надёжность, то можно определить
надёжность всей структуры.

10.

1
A
3
B
5
2
4
Рисунок 3.1
Сечения образуют наборы элементов:
1, 2; 3, 4; 1, 2, 5; 1, 3, 4; 1, 4, 5; 2, 3, 4; 2, 3, 5; 3, 4, 5;
1, 2, 3, 4; 1, 2, 3, 5; 1, 2, 4, 5; 2, 3, 4, 5; 1, 2, 3, 4, 5.

11.

Минимальное сечение – сечение, удаление из которого хотя бы
одного элемента приводит к тому, что оставшееся множество
элементов уже не будет сечением (появится хотя бы один путь…).
Минимальное сечение не содержит в себе других сечений.

12.

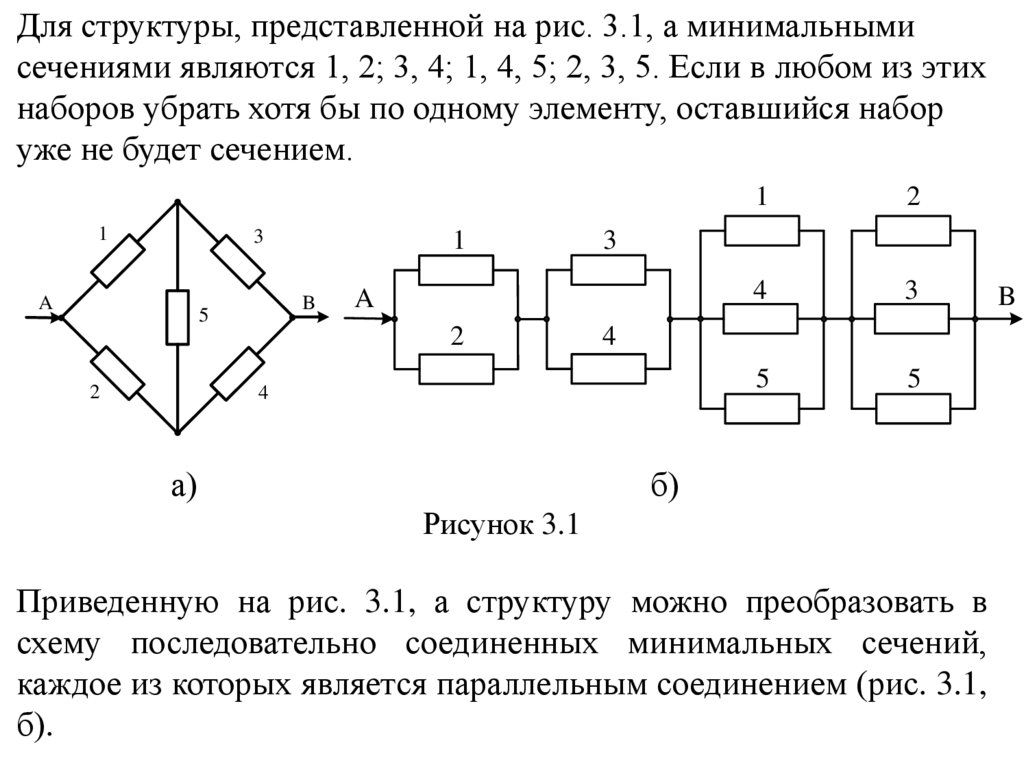
Для структуры, представленной на рис. 3.1, а минимальными
сечениями являются 1, 2; 3, 4; 1, 4, 5; 2, 3, 5. Если в любом из этих
наборов убрать хотя бы по одному элементу, оставшийся набор
уже не будет сечением.
1
3
A
B
5
2
1
4
3
5
5
4
4
а)
2
3
A
2
1
б)
Рисунок 3.1
Приведенную на рис. 3.1, а структуру можно преобразовать в
схему последовательно соединенных минимальных сечений,
каждое из которых является параллельным соединением (рис. 3.1,
б).
B