Похожие презентации:
Оптика
1. ОПТИКА
ХрамовВладимир Николаевич
E-mail: vladimir.khramov@volsu.ru
ОПТИКА
Мультимедийные лекции
кафедры
радиофизики
2. ЛИТЕРАТУРА (основная)
• СтафеевС.К., Боярский К.К., Башнина Г.Л. Основы оптики: Учебное пособие. СПб. :
Питер, 2006. 336 с.
• Калитеевский
Н.И. Волновая оптика: Учебное пособие для вузов. 3-е изд. М. : Высш.
шк., 1995. 463 с.
• Бутиков
Е.И. Оптика: Учебное пособие для студентов физических специальностей
вузов. 2-е изд., перераб. и доп. СПб. : Невский диалект; БХВ-Петербург, 2003. 480 с.
• Ахманов
С.А., Никитин С.Ю. Физическая оптика: Учебник. М. : Изд-во Моск. ун-та,
1998. 656 с.
• Матвеев
А.Н. Оптика: Учебное пособие для физических специальностей вузов. М. :
Высшая школа, 1985. 351 с.
• Родионов С.А. Основы оптики. Конспект лекций. СПб. : СПб ГИТМО, 2000. 167 с.
• Прикладная
физическая оптика: Учебник для вузов / И.М. Нагибина, В.А. Москалев,
Н.А. Полушкина, В.Л. Рудин. 2-е изд., испр. и доп. М. : Высш. шк., 2002. 565 с.
• Сивухин Д.В. Оптика: Учебное пособие. 2-е изд., испр. М. : Наука, 1985. 752 с.
• Нагибина
И.М. Интерференция и дифракция света: Учебное пособие для оптических
специальностей вузов. Л. : Машиностроение, 1985. 328 с.
• Годжаев Н.М. Оптика: Учебное пособие для вузов. М. : Высшая школа, 1977. 432 с.
• Ландсберг
Г.С. Оптика: Учебное пособие для физических специальностей вузов. М. :
Наука, 1976. 928 с.
• Крауфорд Ф. Волны. М. : Наука, 1976. 528 с.
• Борн М., Вольф Е. Основы оптики. 2-е изд. М. : Наука, 1973. 720 с.
3. ЛИТЕРАТУРА (решение задач)
• ГинзбургВ.Л., Левин Л.М. Сивухин Д.В., Четверикова Е.С., Яковлев И.А. Сборник
задач по общему курсу физики. Оптика / Под ред Д.В. Сивухина. 4-е изд. М. :
Наука, 1977. 320 с.
• Иродов
И.Е. Задачи по общей физике: Учебное пособие. 2-е изд. М. : Наука, 1988.
416 с.
• Ильичева
Е.Н., Кудеяров Ю.А., Матвеев А.Н. Методика решения задач оптики /
Под ред. А.Н. Матвеева. М. : Изд-во Моск. ун-та, 1981. 232 с.
4. ЛИТЕРАТУРА (для лабораторных работ)
• АникеевБ.В., Куценко С.А., Храмов В.Н. Методические указания к
лабораторным работам по курсу «Основы оптики». Волгоград : Изд-во ВолГУ,
2006. 96 с.
• Аникеев
Б.В., Храмов В.Н. Оптика: Физический практикум: Поляризация света.
Методические указания к лабораторным работам. Ч.1. Волгоград : Изд-во ВолГУ,
1997.
• Аникеев
Б.В., Храмов В.Н. Оптика: Физический практикум: Дифракция света.
Методические указания к лабораторным работам. Ч.2. Волгоград : Изд-во ВолГУ,
1997.
• Руководство
к лабораторным занятиям по физике / Под ред. Л.Л. Гольдина. М. :
Наука, 1973. 688 с.
• Физический практикум / Под ред. В.И. Ивероновой. М. : Физматгиз, 1962. 956 с.
• Лабораторный
практикум по физике: Учеб. пособие для студентов втузов /
Ахматов А.С., Андреевский В.М., Кулаков А.И. и др.; Под ред. А.С. Ахматова. М. :
Высшая школа, 1980. 360 с.
• Специальный
физический практикум. Ч.3. / Под ред. А.А. Харламова. М. : Изд-во
Моск. ун-та, 1977. 382 с.
5. Основные разделы дисциплины «Оптика»
• Введение. Место оптики в физике• Описание световых волн
• Немонохроматическое излучение
• Дисперсия света
• Отражение и преломление света на границе двух сред
• Основы геометрической оптики
• Интерференция света
• Дифракция света
• Основы голографии
• Распространение света в анизотропных средах
• Рассеяние света
• Генерация света
6. ВВЕДЕНИЕ
Место оптики в физике7. Что такое оптика?
Оптика (от греч. opto’s – видимый, зримый) –раздел физики, в котором изучаются
явления, связанные с распространением и
взаимодействием с веществом коротких
электромагнитных волн, длина которых
лежит в интервале 0,01 нм 1 мм.
8. Оптический диапазон ЭМВ
•Рентгеновский(от 0,01 до 5 нм)
• Ультрафиолетовый (УФ)
(от 5 нм до 380 нм)
• Видимый
(от 380 нм до 780 нм)
•Инфракрасный (ИК)
(от 780 нм до 1 мм)
9. Оптический диапазон ЭМВ
10. Спектр излучения Солнца вблизи поверхности Земли
11. Диапазоны видимой области спектра
Видимые цветаФиолетовый
Синий
Голубой
Зеленый
Желто-зеленый
Желтый
Оранжевый
Красный
Диапазон длин волн, нм
380 450
450 480
480 510
510 550
550 575
575 585
585 620
620 780
12. Тема 1 Описание световых волн
13. Уравнения Максвелла для изотропной несегнетоэлектрической и неферромагнитной среды
Drot
H
j;
t
rot E B ;
t
div B 0;
div D ;
D E;
0
B 0 H;
j E.
H и B – напряженность и индукция
магнитного поля.
E и D – напряженность и индукция
электрического поля.
j – плотность токов проводимости.
– объемная плотность свободных зарядов.
– удельная проводимость.
14. Уравнения Максвелла в вакууме при отсутствии токов (j = 0) и зарядов ( = 0)
Уравнения Максвелла в вакуумепри отсутствии токов (j = 0) и зарядов ( = 0)
D
rot H t ;
rot E B ;
t
div B 0;
div D 0;
D 0 E;
B 0 H
15. Волновое уравнение
Дифференцируем первое уравнение повремени, пользуясь материальными
уравнениями и независимостью
пространственных и временных переменных:
1
2E
rot rot E 0 2
0
t
Используем второе уравнение:
Воспользуемся тождеством из векторного
анализа:
rot rot E = grad div E – 2E
2
1 E
E 2 2 0.
c t
2
2E
H
0 2
rot
t
t
1
c
0 0
Волновое уравнение
- скорость света в вакууме.
с = 299 792 458 м/с
16. Плоские волны
Найдем решение волнового уравнения для скалярной функции Ф=Ф(r,t).Частный случай – одномерная задача, Ф = Ф(z,t).
В момент времени t при z = const функция Ф имеет вполне определенное
значение, одинаковое на всей плоскости z = const.
Такое соответствующее поле называется однородным. В этом случае
волновое уравнение принимает вид:
2Ф 1 2Ф
2 2 0.
2
z
c t
17. Плоские волны
Используем новые формальные независимые переменные: = z – ct, = z + ctФ Ф Ф
;
z
Ф
Ф
Ф
c
c
.
t
С помощью почленного вычитания и аналогичного сложения правых и левых частей
перепишем в виде:
Ф 1 Ф
Ф
Ф 1 Ф
Ф
2
;
2
.
z c t
z c t
В операторном виде:
1
1
Ф 2 Ф;
Ф 2 Ф.
z c t
z c t
Перемножив эти уравнения (с операторной точки зрения):
1 1
Ф 2 2 Ф
z с t z с t
2
2
1 2
2 2 2 Ф 4
Ф
c t
z
18. Плоские волны
Получаем:2Ф 1 2Ф
2Ф
2 2 4
0.
2
z
с t
Интегрируя по , получаем функцию, зависящую только от :
Ф
( ).
Интегрируя далее по , получим решение в виде: Ф ( )d Ф1 ( ) С1 ,
где постоянная интегрирования С1 является функцией , в чем можно
убедиться, проинтегрировав сначала по , а затем по . Отсюда получаем
общее решение в виде:
Ф( , ) Ф1 ( ) Ф2 ( ),
или окончательно в исходных переменных:
Ф( z , t ) Ф1( z ct ) Ф2 ( z ct ).
19. Плоские волны. Физический смысл
Ф Ф2 ( z ct ).Значение аргумента функции в точке z в момент
времени t совпадает со значением аргумента
функции в точке z+ z в момент t+ t, если z=c t,
т.к.
z – ct = z + z – c(t + t) .
Функция Ф2(z – ct) описывает волну произвольной формы, движущуюся со
скоростью v = z/ t = c в направлении положительных значений оси Z. В
процессе движения значение Ф2 в каждой точке волны и форма волны не
изменяются.
Функция Ф1(z+ct) описывает волну произвольной формы, движущуюся
со скоростью с в направлении отрицательных значений оси Z. Значение Ф1 в
каждой точке волны и форма волны в процессе движения не изменяются.
Значение функции Ф для фиксированных z и t является постоянным на
плоскости, перпендикулярной оси Z. Такие волны называются плоскими.
20. Сферические волны
Рассмотрим изотропную волну от точечного источника. Решение волновогоуравнения будем искать в виде Ф(r,t), где r – расстояние от точечного
источника. В сферической системе координат (r, , ) :
2Ф 2 Ф
1
2Ф 1 2Ф ctg Ф
Ф Ф 2
2 2
2
2
2
2
r r r sin
r
r
r
2
1 2
1
Ф
1
2Ф
sin
rФ 2
2 2 2,
r sin
r r 2
r sin
Решение из соображений симметрии не зависит от угловых координат.
Волновое уравнение
Общее решение
1 2Ф 1 2
1 2Ф
Ф 2 2
rФ 2 2 0
2
r r
c t
c t
2
2
1 rФ
rФ 2
0,
2
2
r
c
t
Ф( r , t )
или
Ф1 ( r ct ) Ф2 ( r ct )
.
r
r
Значение Ф в фиксированный момент времени на сфере постоянного радиуса
является постоянным. Такие волны называются сферическими.
21. Плоские гармонические волны
Если Ф1 и Ф2 в являются гармоническими функциями своего аргумента, то волнаназывается гармонической.
Плоская гармоническая волна, распространяющаяся в направлении положительных значений оси Z:
Ф z, t A cos t z / c B sin t z / c .
A, B, – амплитуда волны, – частота волны,
аргумент в квадратных скобках – фаза волны
Плоская гармоническая волна, распространяющаяся в направлении отрицательных значений оси Z:
Ф z, t A cos t z / c B sin t z / c .
Другое определение плоской волны.
Волна, у которой поверхностями постоянных фаз являются плоскости,
называется плоской.
Учитывая, что = сТ = 2 с/ :
Ф z, t A cos t kz ,
где k = /c = 2 / – волновое число.
22. Волновой вектор
Рассмотрим случай бегущей в положительномнаправлении оси Z плоской гармонической волны (см.
рис.). Введем вектор k, называемый волновым, модуль
которого равен волновому числу, а направление
совпадает с направлением распространения волны. Тогда
для произвольной точки с радиус-вектором r можно
записать:
Ф r, t A cos t k r .
Эта формула не зависит от системы координат и
характеризует в общем случае плоскую волну,
распространяющуюся в направлении вектора k.
Примечание
Плоскую гармоническую волну можно рассматривать как частный случай
гармонических волн общего вида
Ф r, t A r cos t g r ,
где А(r) и g(r) зависят от положения r рассматриваемой точки. Поверхности
постоянной фазы такой волны, вообще говоря, не совпадают с поверхностями
постоянной амплитуды (неоднородная волна).
23. Комплексная форма записи плоской волны
iФормула Эйлера e cos i sin
Ф r, t A cos t k r
Ф r, t B sin t k r
Ф(r, t ) A Re exp( i ( t k r ))
Ф(r, t ) B Im exp( i ( t k r ))
Общее решение для плоской волны в комплексной форме:
~ i t k r
Ф r, t A e
,
~
где А - комплексная амплитуда.
Учитывая, что
~ ~ i
A Ae ,
~
Im A
tg
~,
Re A
получаем:
~ i t k r
Ф r, t A e
Любую гармоническую волну можно представить в форме
с действительной амплитудой
24. Плоская световая волна
Для анализа структуры плоской ЭМВ воспользуемся записью уравненийМаксвелла с помощью определения и свойств оператора Гамильтона (наблаоператора):
ex
ey
ez ,
x
y
z
rot A A ,
Тогда уравнения Максвелла примут вид:
div A A .
E
B 0 0 t ;
E B ;
t
0 ;
E 0 .
25. Плоская световая волна
Подставим в уравнения Максвелла для вакуума решения для плоской ЭМВ:E r, t E0 e i t k r ;
B r, t B 0 e i t k r ,
где E0 и B0 – постоянные векторы, не зависящие от координат и времени (в
общем случае их компоненты могут быть комплексными).
Учтем:
e ik r ik e ik r ;
Соотношения, описывающие структуру
плоской световой волны:
i t
e
i e i t
t
k B 0 0 E;
k E B;
k B 0;
k E 0.
26. Структура плоской световой волны
Векторы Е и В плоской волны перпендикулярны вектору k, т.е. направлениюраспространения. Это означает, что плоская ЭМВ является поперечной. E, B и
k составляют тройку взаимно перпендикулярных векторов.
Т.к. k, , 0, 0 – вещественные величины, то это значит, что E и B в плоской
ЭМВ колеблются в одинаковой фазе.
Соотношение между напряженностью электрического поля и магнитной
индукцией плоской ЭМВ в вакууме:
E =cB .
k
k
27. Плотность потока энергии световых волн
Вектор ПойнтингаS E H.
Для плоской волны в вакууме плотность потока энергии:
1
1 2
S S E H E H
EB
E c 0 E 2 .
0
0c
Интенсивность света:
S t c 0 E0 2 cos 2 t
Плотность импульса световой волны:
G
1
c 0 E0 2 .
t
2
S
.
2
c
[Вт/м2]
28. Световое давление
Иоганн Кеплер(1571–1630)
Отклонение хвостов комет
29. Световое давление
Петр НиколаевичЛебедев
(1866–1912)
Если ЭМВ падает нормально на плоскую поверхность и
полностью поглощается, то световое давление
Если поглощение частичное, а остальное отражается и –
коэффициент поглощения, то Sпогл = S и по закону сохранения
энергии Sотр = (1– )S , тогда
S
p (2 )
p cG
S
c
c
Если поверхность, на которую направляется ЭМВ полностью отражающая, то
давление света на нее в 2 раза больше, чем на полностью поглощающую
поверхность.
30. Суперпозиция световых волн
Суперпозиция бегущих плоских монохроматичных световых волнЗаданы две волны, для которых k1= k2= k, 1 = 2 = .
k B1 0 0 E1
k E B
1
1
k B1 0
k E1 0
k B 2 0 0 E 2
k E B
2
2
k B 2 0
k E 2 0
E1 cB1
E2 cB2 .
Принцип суперпозиции полей:
k B 0 0 E ;
k E B ;
k B 0 ;
k E 0 ;
E cB .
E E1 E 2 ; B B1 B 2 ,
Две плоские монохроматические бегущие ЭМВ с
одинаковой частотой, распространяющиеся в одном
и том же направлении, в результате сложения дают
плоскую монохроматическую ЭМВ той же частоты,
распространяющуюся в том же направлении.
31. Суперпозиция световых волн
БиенияРассмотрим случай: 1 2 , E1 E2 , k1 k2 :
E1x E0 cos 1t k1 z
E2 x E0 cos 2 t k2 z .
E E x E1x E2 x E0 cos 1t k1 z E0 cos 2 t k2 z
k k 2 1 2
k k2
2
2 E0 cos 1
t 1
z cos
t 1
z
2
2
2
2
z 1
z
1
Незатухающая бегущая
2 E0 cos 1 2 t cos 1 2 t .
в сторону +Z
c 2
c
2
немонохроматическая
волна.
Ex
2E 0
0
Если | 1 – 2 | 1 + 2 , то соотношения
описывают ЭМВ с с частотой ( 1 + 2) / 2 и
медленно меняющейся амплитудой.
z
Гармонические колебания с медленно изменяющейся
амплитудой называются биениями.
= | 1 – 2| -частота биений.
32. Суперпозиция световых волн
Стоячие волныСуперпозиция двух монохроматических волн с 1 = 2 = , E10 = E20 = E0 , E1 E2
и распространяющихся навстречу друг другу:
E1 E0 cos t kz ;
E2 E0 cos t kz ,
– разность фаз.
E E1 E2 2 E0 cos kz cos t .
2
2
2 E0 cos kz
2
- амплитуда колебаний
напряженности поля в
заданной точке z
Узлы – точки оси Z, где
Узел
Пучность
/2
cos kz / 2 0
Пучности – точки оси Z, где
cos kz / 2 1
33. Суперпозиция световых волн
Стоячие волныМагнитная индукция в данном случае
получается
из
суперпозиции
магнитных
индукций волн:
Суммарное поле:
E0
B
1 c cos t kz ;
B2 E0 cos t kz .
c
2 E0
B B1 B2
sin kz sin t .
c
2
2
Объемная плотность энергии
электромагнитного поля
1
w E D H B
2
Энергия стоячей волны, заключенная между
соседними узлами и пучностями, остается
постоянной с течением времени.
34. Поляризация световых волн
Поляризация света – это физическая характеристикаоптического излучения, описывающая поперечную
анизотропию световых волн, т.е. неэквивалентность
различных направлений в плоскости, перпендикулярной
направлению распространения волны.
Световые волны, у которых направления колебаний
векторов электрического E и магнитного H полей
сохраняются неизменными в пространстве или
изменяются по определенному закону, называются
поляризованными.
35. Поляризация световых волн
Если вектор E световой волныколеблется лишь в одной неизменной
в пространстве плоскости, то такая
волна называется линейно или
плоско
поляризованной.
При
линейной поляризации плоскость,
содержащая волновой вектор k и
вектор E, называется плоскостью
поляризации волны.
Если
колебания
вектора
E
совершаются так, что его конец
описывает окружность в плоскости,
перпендикулярной
направлению
распространения волны k, то такая
волна называется поляризованной
по
кругу,
если
эллипс,
то
эллиптически поляризованной.
36. Поляризация световых волн
Световая волна, в которой различные направления вектораE в поперечной к направлению распространения волны
плоскости равновероятны, называется естественной
(естественно
поляризованной
или
неполяризованной).
37. Поляризация световых волн
Закон МалюсаI( )=I0cos2
Поляризаторы
38. Поляризация световых волн
Суперпозиция двух линейно поляризованных волнРассмотрим суперпозицию двух линейно поляризованных волн с
одинаковыми частотами , амплитудами электрических полей E1 и E2,
распространяющихся в одном направлении (вдоль оси Z декартовой системы
координат) со сдвигом фаз . Пусть вектор E1 колеблется в плоскости XZ, а
вектор E2 – в плоскости YZ:
E1 y E1z 0 ;
E1x ( z , t ) E10 sin( t kz ) ,
E2 y ( z, t ) E20 sin( t kz ) , E2 x E2 z 0.
E ={Ex; Ey; Ez}= E1+E2
E y E20 sin( t kz )cos E20 cos( t kz )sin .
Ex
E x2
E y E20
cos E20 sin 1 2 .
E10
E10
Состояние поляризации
суммарного поля в общем виде:
2
2
E
Ex
Ex E y
y
2
2
cos
sin
.
2
2
E10 E20
E10 E20
39. Поляризация световых волн
Основные случаи состояния поляризации1)
cos 0 ; sin 1
E10 E 20
2
2
E
Ex
y
1.
2
2
E10 E20
Эллиптическая поляризация
Если при наблюдении навстречу волне вращение вектора E в
фиксированной плоскости (перпендикулярной волновому вектору)
происходит по часовой стрелке, то такая волна называется правой
эллиптически поляризованной волной, если против часовой
стрелки – левой эллиптически поляризованной волной.
2)
cos 0 ; sin 1
E10 E 20
Ex2 E y2 E02
Круговая (циркулярная)
поляризация
40. Поляризация световых волн
Основные случаи состояния поляризации3)
cos 0
(общий случай)
Эллиптическая поляризация
Главные оси эллипса не совпадают с осями координат.
Ориентация эллипса зависит от сдвига фаз . При
этом эллиптичность поляризации остается и при E10 E 20
4)
cos 1 , sin 0
Ey
Ey
Ex
Ex
0;
0.
E10 E20
E10 E20
Линейная поляризация
41. Поляризация световых волн
Световая волна с любой поляризацией может бытьпредставлена в виде суперпозиции двух линейно
поляризованных во взаимно-перпендикулярных плоскостях
волн. Поэтому можно сказать, что электромагнитные волны
обладают двумя независимыми состояниями поляризации.
42. Параметры Стокса
Так как эллиптическая поляризацияявляется общим случаем сложения двух
ортогональных волн с одинаковой
частотой, то на практике часто удобно
задавать этот эллипс. Пусть в заданной
системе координат задан произвольно
ориентированный эллипс.
tg - эллиптичность,
- азимут.
Состояние поляризации часто определяют с помощью четырех параметров Стокса,
образующих вектор Стокса. Эти параметры имеют размерность интенсивности и
измеряются экспериментально: S 0 , S1 , S 2 , S3
2
S 0 E102 E20
~I
2
S1 E102 E20
S 2 2 E10 E20 cos
S 2 E E sin .
10 20
3
Из них независимыми являются только три.
Параметры Стокса между собой связаны:
S 0 S12 S 22 S 32
S1 S 0 cos 2 cos 2
S 2 S 0 cos 2 sin 2
S 3 S 0 sin 2 .
43. Смысл параметров Стокса
S0 пропорционален интенсивности света.Обычно его нормируют на 1 (нормированный вектор Стокса).
S1 задает степень преобладания линейной поляризации вдоль оси X над
поляризацией вдоль оси Y (при линейной поляризации вдоль OX S1=+1, при
линейной поляризации вдоль OY S1= -1).
S2 задает преобладание линейной поляризации под углом +450 к оси OX
+ 450 S2 = +1
- 450 S2 = -1
S3 определяет направление вращения вектора E.
Для правого вращения S3 > 0, для левого вращения S3 < 0.
Для круговой поляризации S3 = 1.
44. Сфера Пуанкаре
Наглядную интерпретацию нормированного вектора Стокса можно получить,если рассматривать три компоненты S1, S2, S3 как координаты в декартовой системе
координат, а S0 - как единичный радиус сферы. Полученная таким образом сфера, на
которой расположен конец вектора Стокса, соответствующий любой форме
поляризации, называется сферой Пуанкаре. При описании этой сферы обычно
используют географическую терминологию. На полюсах расположены две
циркулярные поляризации. На экваторе – линейные поляризации всех азимутов.
Параллели являются линиями равной эллиптичности, а меридианы – линиями равных
азимутов.
45. Примеры векторов Стокса
Естественный свет:1, 0, 0, 0
Линейно-поляризованный свет вдоль оси OX:
1, 1, 0, 0
Линейно-поляризованный свет вдоль оси OY:
1, 1, 0, 0
Линейно-поляризованный свет под углом 45 к оси OX: 1, 0, 1, 0
Правая круговая поляризация:
1, 0, 0, 1
Левая круговая поляризация:
1, 0, 0, 1
.
46. Тема 2 Немонохроматическое излучение
47. Немонохроматическое излучение
Реальное излучение имеет конечную продолжительность ипроисходит
со случайно изменяющимися амплитудой и фазой.
Ограниченность по времени и монохроматичность
исключают друг друга.
Реальную ЭМВ можно представить в виде наложения
монохроматических волн с различными частотами в
соответствии с принципом суперпозиции полей.
С математической точки зрения спектральный состав
излучения анализируется с помощью
Фурье–преобразований
48. Ряд Фурье в действительной форме
a0f t
a n cos n t bn sin n t ,
2 n 1
где
T 2
T 2
2
2
2
; an
f t cos n t dt ; bn
f t sin n t dt .
T
T T 2
T T 2
49. Интеграл Фурье
1i t
f t
F
e
d ,
2
где
F f t e i t dt
(комплексный спектр или просто спектр функции f(t)).
50. Спектр амплитуд и спектр фаз
cos nan
a n2 bn2
; sin n
bn
a n2 bn2
; An a n2 bn2 ; tg n
bn
,
an
A0
f t
An cos n t n .
2 n 1
Совокупность An называется спектром амплитуд функции f(t), а совокупность n – спектром
1
f t
A cos t d ,
2 0
A 2 F ;
tg
Im F
.
Re F
Периодические функции характеризуются дискретными
спектрами, а непериодические – непрерывными
51.
1. Спектр периодически повторяющихсяпрямоугольных импульсов
sin n / 2
An 2 U 0
;
T
n / 2
n 0.
An
n
0
2. Спектр прямоугольного импульса
F U 0
sin / 2
;
/ 2
A 2U 0
sin / 2
;
/ 2
A ( )
/2
0
1
2
3
0.
52. Соотношение между длительностью импульса и шириной спектра
Длительностью импульса называется промежуток времени t, втечение которого импульс существенно отличается от 0.
Шириной спектра называется интервал частот , на котором амплитуда
спектра существенно отлична от 0.
Ууниверсальная закономерность: ширина спектра обратно
пропорциональна длительности импульса:
t 1 .
Точное соотношение зависит от формы исследуемого сигнала и от точного
определения величин t и .
53. Модулированные волны
Гармоническоеколебание,
описывающее
волну,
характеризуется
амплитудой,
частотой
и
фазой.
Изменение этих параметров в процессе колебания
называется модуляцией, а волны при этом –
модулированными.
54. Амплитудная модуляция
Общий случайf t A0 a t cos t
Пусть
a t a0 cos t,
Тогда
или
a t A0 .
.
f t A0 a0 cos t cos t
1
1
f t A0 cos t a0 cos t a0 cos t ,
2
2
55. Модуляция частоты и фазы
tСвязь частоты и фазы
t t dt
t
0
d
.
dt
Гармоническая модуляция частоты
t 0 cos t ,
t
t t dt 0t
0
sin t.
Гармоническая модуляция фазы
t 0t sin t
d
t
0 cos t
dt
56. Модуляция частоты и фазы
Частотная и фазовая модуляции полностью эквивалентны только тогда, когдаони гармонические. При негармонической модуляции эквивалентность
невозможна и структура сигналов различна.
Для частотной модуляции:
{медленное изменение сигнала (малая )}
{большие колебания по фазе ( / )}
Для фазовой модуляции:
{медленное изменение сигнала (малая )}
{малые амплитудные колебания частоты ( )}
57. Волновые пакеты
В отличие от распространения в вакууме, в среде скорость ЭМВменьше c = const и зависит от частоты. Зависимость скорости волны от
частоты называется дисперсией.
k 1||k 2 ;E1||E 2 ;
Суперпозиция двух волн с разными частотами
E1 z , t E0 cos 1t k1 z
E 2 z , t E0 cos 2 t k 2 z .
Фазовая скорость определяется из условия: t kz const
dz
vф v
dt k
Суперпозиция двух и более волн с различными частотами составляет группу
волн (волновой пакет).
58. Групповая скорость
E z, t E1 E2t
z
t
z
2 E0 cos 1 2 k1 k 2 cos 1 2 k1 k 2 .
2
2
2
2
Ex
dz 1 2
u
.
dt k1 k 2
2E 0
0
E(t)
t
z
Скоростью группы волн или групповой скоростью u называется скорость
движения максимума огибающей амплитуды группы волн при условии, что
волновой пакет (импульс) движется как единое целое (не деформируясь).
d
u .
dk
59. Формула Рэлея
(Rayleigh Robert John, 1842–1919)u
d d (v k )
dv
v k
dk
dk
dk
k
2
;
dv
u v
d
Формула Рэлея
dk
2
d
2
60. Тема 3 Дисперсия света
61.
Рассмотрим распространение световых волн в однородных изотропныхдиэлектриках, где диэлектрическая проницаемость не зависит от координат.
Будем считать, что она не зависит и от времени.
В уравнения Максвелла замена:
0 0
( - относительная диэлектрическая проницаемость)
Фазовая скорость:
n
v
1
c c
,
0 0
n
– коэффициент (показатель) преломления
диэлектрика.
v 2 v
.
Длина волны:
Волновое число: k
2
.
v
62. Классическая электронная теория дисперсии
Дисперсия света – зависимость скоростираспространения световых волн от их частоты
Дисперсия проявляется лишь в распространении немонохроматических волн,
т.к. ее монохроматические составляющие с различными частотами
распространяются с различными скоростями. Дисперсия является следствием
зависимости поляризованности атомов от частоты.
Для нахождения явного вида ( ), входящей в материальные уравнения,
воспользуемся микроскопической классической теорией взаимодействия
электромагнитного поля волны с веществом. Микроскопическая теория
исходит из идеализированной модели строения вещества. Наибольшей
простотой отличается модель газообразной среды, т.к. для нее в первом
приближении можно не учитывать взаимодействие атомов или молекул и
считать, что действующее на отдельный атом поле совпадает со средним
полем ЭМВ. В таких условиях для получения макроскопического
материального уравнения достаточно рассмотреть действие поля ЭМВ на
изолированный атом.
63. Классическая электронная теория дисперсии
В классической теории дисперсии электрон, с которым взаимодействуетэлектромагнитное поле (внешний, или оптический электрон), в атоме
рассматривается как затухающий дипольный осциллятор, характеризуемый
определенной собственной частотой о и постоянной затухания .
Уравнение его движения в поле E(t) = Eoe–i t световой волны имеет вид:
r r 02r
e
E t ,
m
где r – смещение электрона из положения равновесия, e и m – заряд и масса
электрона.
e/m
i t
r (t ) 2
E(t )
Решение: r (t ) r0 e
2
0 i
Дипольный момент атома p(t), индуцированный полем E(t):
e2 / m
p(t ) er 2
E(t )
2
0 i
64. Классическая электронная теория дисперсии
Если N – концентрация электронов с собственной частотой колебаний 0, тополяризованность (поляризация) P среды определяется как:
P Np
С другой стороны:
P 0 E
где – линейная диэлектрическая восприимчивость среды, которая в общем случае
зависит от частоты . Векторы D, E и P связаны соотношением:
D 0E P
Относительная диэлектрическая проницаемость:
( ) 1 ( )
e2 N
( ) 1
m 0 02 2 i
65. Классическая электронная теория дисперсии
nПоказатель преломления, а следовательно, и скорость ЭМВ зависят от
частоты. n – комплексная величина:
n( ) n in
2
02 2
e2 N
2
;
n n 1
2
2
2
2
2
0m
0
2
2n n e N
.
0 m 2 2 2 2 2
0
Для прозрачных или частично прозрачных
в оптическом диапазоне диэлектриков:
2
2
и n 0
2
2 2
0
e2 N
n 1
0 m 02 2
2
Для различных ансамблей электронов
с собственными частотами 0i и концентрацией Ni
2
Ni
e
2
n 1
0 m i 02i 2
66. Нормальная дисперсия
Вдали от собственных резонансов n’( ) ~ 1n 2 1 n 1 n 1 2 n 1
(для прозрачных диэлектриков, разреженных газов)
Ni
e2
n 1
2 0 m i 02i 2
Дисперсионная кривая
.
Если действительная часть
показателя преломления
увеличивается с ростом частоты,
то дисперсия называется
нормальной.
Нормальная дисперсия
наблюдается во всей области
прозрачности диэлектриков.
67. Нормальная дисперсия
Статическое значение показателя преломления(для малых частот ( << 0i)) :
Ni
e2
n 1
2 0 m i 02i
Для больших частот ( >> 0i )
n 1 и n 1
e2
1
n 1
2 Ni
2 0 m
Для коротковолнового излучения диэлектрик является оптически
менее плотной средой, чем вакуум. Например, для рентгеновского
излучения может наблюдаться полное отражение.
При очень больших частотах характер связи электронов роли не
играет, а показатель преломления n зависит лишь от общей
концентрации всех электронов.
68. Аномальная дисперсия
Вблизи собственных частот нельзя пренебречь затуханием .n является непрерывной функцией. С учетом не слишком большого поглощения
(n ~ 1)
2
2
2
0
e N
n
1
;
2
2 2
2 2
2
m
0
0
2
n e N
.
2
2
2
2
2
2 0 m
0
Вблизи
резонансных
частот
вещественная
часть
показателя
преломления уменьшается с ростом
частоты (аномальная дисперсия).
Мнимая часть показателя преломления в
общем случае определяет величину
поглощения.
Поэтому
область
аномальной дисперсии соответствует
области поглощения световых волн
данным веществом.
69. Аномальная дисперсия
70. Тема 4 Отражение и преломление света на границе двух диэлектриков
71. Отражение и преломление света на границе двух диэлектриков
Граничные условия для векторовD2 n D1n ; B2 n B1n ;
поля световой волны на границе между
двумя диэлектриками при отсутствии
E2 E1 ; H 2 H1 ,
свободных зарядов и токов
проводимости
где , n – индексы тангенциальной (касательной к
границе раздела) и нормальной компоненты
вектора соответственно.
Частота ЭМВ при отражении и преломлении не
меняется:
0
1
2
.
Плоскость, в которой лежат волновой вектор
k0 и нормаль к поверхности раздела n в
точке падения луча, называется
плоскостью падения
Волновые векторы падающей, отраженной и преломленной волн лежат в
одной плоскости.
72. Отражение и преломление света на границе двух диэлектриков
n1 sin 0 n2 sin 2Закон преломления (закон Снеллиуса)
(Snellius Willebord 1591–1626)
n2
n21
n1
– относительный показатель преломления
1 0
Закон отражения
sin 0
n21
sin 2
73. S- и P-поляризация
Вектор E0 в падающей волне может иметь произвольный азимут (угол между E иплоскостью падения. Разложим векторы электромагнитного поля на две составляющие:
перпендикулярные плоскости падения (будем обозначать их индексом s (или ) и
параллельные плоскости падения (будем обозначать их индексом p (или )):
E0 E0 p E0s ;
E1 E1 p E1s ;
E2 E2 p E2s .
(E p ; B s ; k )
(E s ; B p ; k )
правовинтовые тройки векторов и
образуют сами плоские ЭМВ.
E 2 Es2 E 2p
Плотность потока энергии исходной волны равна сумме плотностей потока энергии волн, на
которые она разлагается.
Плоскую волну с произвольным азимутом можно разложить на сумму волн, у одной из которых
Ep (p – поляризация) лежит в плоскости падения, а у другой Es (s – поляризация) –
перпендикулярна ей.
Изучив поведение этих волн на границе с учетом принципа суперпозиции и аддитивности (в
данном случае) плотностей потока энергии, получим поведение ЭМВ с произвольным
азимутом.
74. Отражение и преломление s-поляризованной волны
E0 E1 E 2 ;(H 0 H1 ) H 2 .
k 0 k0 e k 0 ;
k 1 k1 e k1 ;
k 2 k1 e k 2 .
Z
Граничные условия
– волновое сопротивление (импеданс) среды
Для вакуума
H e k E
1
Z
1
E 0 n
E0
A B C D A C B D A D B C
1
E0 e k 0 n E1 e k1 n 1 E2 e k 2 n
Z1
Z2
Z
0
377 Ом
0
H e k E E 0 n
1
Z E0
H E e k n
1
Z
75. Отражение и преломление s-поляризованной волны
E1 E21 E E ;
0
0
e n E1 e n Z1 E2 e n .
k1
k2
k 0
E0
Z 2 E0
Rs
Z 2 cos 0 Z1 cos 2
;
Z 2 cos 0 Z1 cos 2
2Z 2 cos 0
Ts
.
Z 2 cos 0 Z1 cos 2
Обобщенные формулы Френеля
для s – поляризации
E1
– амплитудный
R коэффициент отражения
E0
E2
T
E0
– амплитудный
коэффициент пропускания
sin 0 2
Rs
;
sin 0 2
2 cos 0 sin 2
Ts
.
sin 0 2
Формулы Френеля
для s – поляризации
для диэлектриков
76. Отражение и преломление s-поляризованной волны
При отражении света от диэлектрика с n21>1 фаза отраженной волныизменяется на 1800.
При отражении света от диэлектрика с n21<1 фаза отраженной волны не
изменяется.
При преломлении скачка фазы не происходит.
Случай полного внутреннего отражения (n21<1 , 0> п) требует отдельного
рассмотрения.
77. Отражение и преломление p-поляризованной волны
Граничные условияE Z H e k ;
H 0 H1 H 2 .
n H0
E0 E1 E 2 ;
Z1 cos 0 Z 2 cos 2
Rp
;
Z1 cos 0 Z 2 cos 2
Tp
2 Z 2 cos 0
,
Z1 cos 0 Z 2 cos 2
Обобщенные формулы Френеля
для p – поляризации
Rp
tg 0 2
;
tg 0 2
2 cos 0 sin 2
Tp
.
sin 0 2 cos 0 2
Формулы Френеля
для p – поляризации
для диэлектриков
1
.
H0
78. Явление Брюстера
0 БДля p–поляризованной волны при некотором угле падения
называемом углом Брюстера, отраженная волна отсутствует, R
т.е.
p Б 0
Это называется явлением Брюстера (Brewster David, 1781 – 1868) (1815 г.).
з 2
tg з
;
2
n2
n21 .
n1
При переходе через угол Брюстера фаза колебаний
отраженной волны скачком меняется
0 на
Б . При
при падающей волне с произвольным азимутом отражается
лишь s – поляризованная компонента.
Стопа Столетова
79. Нормальное падение света
При нормальном падении света0 2 0
понятия s– и p– поляризаций теряют смысл и формулы дают один и тот
же результат.
Для диэлектрика 1 2 Z
n1 n2
R
;
n1 n2
1
n
2n1
T
.
n1 n2
80. Энергетические соотношения при преломлении и отражении
Энергетическим коэффициентом отражения называетсяабсолютное значение отношения нормальных компонент
векторов Пойнтинга в отраженной и падающих волнах:
S1n
S1 n
S0n S 0 n
Энергетический коэффициент пропускания вводится аналогичным
образом для преломленной волны:
S 2n S 2 n
S0n S 0 n
e k 0 n e k1 n cos 0
k 0 n k1 cos 0 ;
2
R ;
k 2 n k 2 cos 2 ,
Z1 cos 2
2
T
Z 2 cos 0
81. Энергетические соотношения при преломлении и отражении
Z cos 0 Z1 cos 2s 2
cos
Z
cos
Z
2
1
0
2
Z1 cos 0 Z 2 cos 2
p
Z
cos
Z
cos
0
2
2
1
2
s
2
4 Z1Z 2 cos 0 cos 2
Z 2 cos 0 Z1 cos 2 2
p
4 Z1Z 2 cos 0 cos 2
Z1 cos 0 Z 2 cos 2 2
.
1
При 0 = 0 для 1 = 2
n n
’ 1 2
n1 n2
2
’
4n1n2
n1 n2 2
82. Полное внутреннее отражение
Из закона Снеллиуса следует, что существуетпредельный (или критический) угол п падения, при
котором угол преломления
2
2
sin п
0
n2
n1
угол преломления 2 имеет обычную геометрическую
п интерпретацию, и коэффициенты R и T являются вещественными.
0 > п
- не существует вещественного угла преломления 2 , т.к. закон
Снеллиуса дает для sin 2 значение больше единицы, а для cos 2 – чисто
мнимое значение:
n12
n12
2
cos 2 1 2 sin 0 i 2 sin 2 0 1
n2
n2
sin 2
n1
sin 0 > 1 .
n2
Im
83. Полное внутреннее отражение
x sin 2 z cos 2E2 E20 exp i t
v2
i z cos 2
x
.
E20 exp
exp i t
v
v
/
sin
2
2 2
I
II
Волна во второй среде (преломленная)
В такой записи сомножитель I означает
комплексную амплитуду волны II,
распространяющейся вдоль оси X со
скоростью v 2 / sin 2
n1
x
sin
0
n2
2 n1
E2 E20 exp
z sin 0 1 exp i t
n
v
2
2 2
2
Знак (+) в первой экспоненте соответствует безграничному возрастанию поля в
среде, что лишено физического смысла. Поэтому остается (–), что
соответствует быстро убывающей с ростом z амплитуде волны,
распространяющейся во второй среде вдоль X. Практически эта неоднородная
волна существует лишь в поверхностном слое второй среды толщиной
порядка длины волны. Причем фазовая скорость этой неоднородной (и
соответственно не плоской) зависит как от свойств среды, так и от угла
падения.
84. Полное внутреннее отражение
Формулы Френеля для ПВОRp
2
2
n21
cos 0 i sin 2 0 n21
2
n21
cos 0 i
sin
2
Rs
2
0 n21
2
cos 0 i sin 2 0 n21
2
cos 0 i sin 2 0 n21
2
p, s Rp, s 1
d
2 / 2
2
глубина проникновения
n1
sin 0 1
n2
(амплитуда поля на глубине d падает в е раз):
85. Полное внутреннее отражение
R p exp i p ; Rs exp i stg
p
2
2
sin 2 0 n21
2
n21
cos 0
p s
2
sin 2 0 n21
s
; tg
;
2
cos 0
p s
2
sin 2 0 n21
tg cos 0
2
sin 2 0
86. Полное внутреннее отражение (примеры)
Отражательные призмыРомб (параллелепипед) Френеля
54 o37
87. Полное внутреннее отражение (примеры)
Схема образования миража88. Полное внутреннее отражение (примеры)
Мираж89. Полное внутреннее отражение (примеры)
Мираж90. Полное внутреннее отражение (примеры)
Огранка бриллиантов91. Полное внутреннее отражение (примеры)
92. Распространение света в проводящих средах
~ i ;0
n~ ~ n i .
cos 2 1
В сильно поглощающих средах и металлах мнимая часть
преобладает над вещественной.
sin 0
2
n i
2
R s s e i s ;
i
Rp pe p .
При линейной поляризации падающего света с произвольным азимутом в
отраженной волне появляется сдвиг фаз, приводящий к эллиптической
поляризации отраженного света. Отраженный свет остается линейно
поляризованным, если:
падающий свет s– или p–поляризован
0 0
0
2
93. Распространение света в проводящих средах
2n
1
2
*
RR
n 1 2 2
1 n i
R
1 n i
Нормальное падение света
Оптические постоянные для металлов ( =589,3 нм)
Металл
n
Na
0,97
0,044
2,42
Ag
0,94
0,20
3,44
Cd
0,84
1,13
5,01
Al
0,83
1,44
5,23
Au
0,82
0,47
2,83
Hg
0,77
1,60
4,80
Cu
0,71
0,62
2,57
Pb
0,54
3,46
3,25
Fe
0,33
1,51
1,63
94. Распространение света в проводящих средах
Волновой вектор прошедшей в металл волны при нормальном падении имееттолько z – составляющую:
E 2 z , t 2 E0
1 n i
z
n
exp
exp
i
t
z
2
2
c
c
1 n
0
c
d
2
Закон Бугера
глубина проникновения света в металл
I I 0e
z
4
I I 0 exp
z
0
95. Тема 5 Геометрическая оптика
96. Уравнение эйконала
Волновое уравнение для световой волны в среде с показателем преломленияn=c/v:
n 2 2Ф
Ф 2 2 0
c t
2
Для монохроматической волны Ф(r, t ) (r ) exp i t
2 n 2 k 02 0
где k0= /c – волновое число в вакууме. Волновое число в среде k=nk0.
2
1 2 2
(ln
)
ln
.
2
2
x
x
x
Решение ищем в виде:
2 (ln ) (ln ) n 2 k 02 0
2
(r ) A(r ) exp iS (r )
Вещественная скалярная функция S(r) называется эйконалом
(от греческого eikon – изображение).
97. Уравнение эйконала
(ln A) (ln A) S n k i S 2 (ln A) S 02
2
2
2
2
0
2
Приравнивая нулю вещественную и мнимую части, получим два уравнения
для определения А(r) и S(r):
2 (ln A) (ln A) 2 S 2 n 2 k 02 0 ;
2
S 2 (ln A) S 0 .
Для оптического диапазона длина волны много меньше расстояния L, на
которых амплитуда волны существенно меняется (порядка размера
оптических элементов). Поэтому первыми двумя слагаемыми в первом
уравнении можно пренебречь (их сумма имеет порядок 1/L2). Тогда это
уравнение в оптическом диапазоне принимает вид уравнения эйконала:
S 2 n 2 k02
Градиент от функции S(r) направлен по нормали к поверхности S=const.
Поэтому эйконал S описывает поверхности постоянной фазы волны, а S
приводит к понятию луча, т.е. к представлению о движении световой энергии
в данной точке в определенном направлении. Лучом называется линия,
касательная к которой совпадает в каждой точке с вектором S.
98. Уравнение эйконала
Анализ распространения света в лучевом приближении составляет предметгеометрической оптики. Этот подход оправдан всегда, когда
2 A 1
2
A
В геометрической оптике не учитываются дифракционные эффекты
99. Принцип Ферма (Fermat Pierre, 1601 – 1675)
В однородной среде S=k r (k=const) и лучи являются прямымипараллельными линиями, а фронт волны – плоскостью,
перпендикулярной лучам.
Для неоднородной среды лучи имеют более сложную
конфигурацию. Пусть точки P1 и P2 соединяются лучом L (см.
рис.). Вычислим изменение фазы вдоль луча:
d S S d r S d r k0 n(r) d l
где dr направлен по лучу и совпадает с S, dl – элемент длины пути. Для
изменения фазы находим:
P2
P2
S d S k 0 n(r ) d l
P1
P1
P2
n(r) d l
- оптическая длина пути
P1
Интеграл (оптическая длина пути) вдоль луча имеет стационарное значение, т.е.
первая вариация S относительно соседних путей интегрирования равна нулю.
Реальный луч отличается от остальных кривых, соединяющих две заданные
точки, тем, что соответствующая ему оптическая длина имеет стационарное
значение, т.е. малое изменение траектории не приводит к изменению
оптической длины.
100. Принцип Ферма (Fermat Pierre, 1601 – 1675)
К принципу Ферма можно подойти и с другой стороны.Учтем что dt=dl / v – время прохождения пути dl со скоростью v, а n(r) =
c / v(r). Тогда
P2
P2
dl
dl
v
v
P
P
S k0c
1
1
где интеграл здесь дает время, затрачиваемое на прохождение пути от P1 и P2.
Лучом, соединяющим две точки, является тот путь, который делает
стационарным время, затрачиваемое светом на его прохождение.
Формулировка о стационарности времени прохождения пути между двумя
точками, с одной стороны, утверждает экстремальный характер этого времени,
а с другой стороны, не исключает наличия нескольких путей с одинаковым
временем прохождения.
101. Вывод закона преломления из принципа Ферма
Пусть требуется соединить лучом две точки P1 и P2,находящиеся
в
однородных
средах
с
коэффициентами преломления n1 и n2, разделенных
плоской границей (см. рис.). В каждой однородной
среде луч – прямая линия. Из геометрии рисунка
получаем для полного времени распространения
света между точками P1 и P2:
n1 2
n2 2
2
t
l1 x
l2 ( a x ) 2 .
c
c
t x 0 - условие стационарности
x
l12 x 2 sin 0 , (a x)
n1 x
c
l12 x 2
l22 (a x) 2 sin 2 ,
n1 sin 0 n2 sin 2
n2 ( a x )
c
l22 (a x) 2
0
102. Центрированные оптические системы
Линзами называют детали из оптически прозрачных однородных материалов,ограниченные двумя преломляющими поверхностями, из которых хотя бы одна
является поверхностью тела вращения (сфера, асферическая или
цилиндрическая поверхность).
Параксиальное приближение
sin ;
tg ;
cos 1 .
103. Преломление на первой поверхности
В точке P1 закон Снеллиуса впараксиальном приближении имеет
вид:
/ /
n1 1 n1 1
Геометрические соотношения
между углами
1 1 ; 1/ 1/
В параксиальном приближении
n1/ 1/
n1 n1/
x1/ x1
x1
n1 1
r1
x1
r1
n1/ 1/ 1 k1 n1 1
/
x
0
1
1
x1
Величина k1=(n1/–n1)/r1 называется преломляющей силой первой
поверхности.
1
Преломляющая матрица первой
R1
поверхности
0
k1
1
104. Распространение луча внутри линзы
x2 x1/ 1/n1/ n2 , 1/ 2 ,
1
n2 2
x /
2 n1
1
T21
n/
1
0
1
Передаточная матрица
0 / /
n
1 1
1 x /
1
105. Преломление на второй поверхности
Величина k2=(n2/ –n2)/r2 называетсяпреломляющей силой второй
поверхности, а матрица R2 –
преломляющей матрицей
второй поверхности:
1 k 2
R2
0
1
Знаки всех величин в приведенных выражениях необходимо брать с
учётом правила знаков: если встречаемая лучом преломляющая поверхность
выпуклая, то её радиус кривизны надо брать с положительным знаком, а если
вогнутая – с отрицательным; углы , отсчитываемые от оси Z против часовой
стрелки, положительны, а по часовой стрелке – отрицательны; расстояния,
отсчитываемые по Z (по рис. – слева направо), положительны, а против Z
(справа налево) – отрицательны; расстояния от оси Z, отсчитываемые вверх,
положительны, вниз – отрицательны.
106. Распространение луча через оптическую систему
n2/ 2/n1 1
n1 1 b
S 21
/ R2T21 R1
x1
x1 d
x2
a n1 1
c x1
det S 21 1
a k1 k 2 k1k 2 / ;
n1
b 1 k2 / ;
n1
c 1 k1 / ;
n1
d / ,
n1
где a, b, c, d
Гаусса.
называются постоянными
Независимыми являются только три из четырех
постоянных Гаусса.
Матрица
S21
полностью
описывает
рассмотренную оптическую систему.
107. Преобразование луча от плоскости предмета к плоскости изображения
n2/ 2/ 1/ / /
x l n2
0 b
1 d
n2/ 2/
n1 1
/ Q21
x
x
0 n1 1
a 1
c l n1 1 x
b al / n1
al / l cl
Q21 bl /
/ d /
n2 n1 n1
n2
a
/
/
c al / n2
Матрица преобразования
предмета к изображению
108. Преобразование луча от плоскости предмета к плоскости изображения
x/M
x
увеличение оптической системы
Под изображением понимается такое отображение плоскости предмета на
плоскость, называемую плоскостью изображения, когда все лучи, выходящие
из точки предмета, сходятся после преломления в оптической системе в одной
точке плоскости изображения, и все точки отображаются с одинаковым
увеличением.
/
/
bl
al l cl
d
0
/
/
n2
n2 n1 n1
Из определения увеличения имеем:
al /
1
al
M c / или
b
M
n1
n2
Матрица преобразования от предмета к
изображению принимает вид:
1 M a
Q21
,
M
0
det Q21 1 .
109. Кардинальные элементы оптической системы
Плоскости H и H/, увеличение для точек которых М = 1, называются главнымиплоскостями, а их пересечения с осью системы (ось Z) – главными
точками системы.
n1 (1 b)
n2/ (c 1)
lH
; lH /
a
a
где lH – отсчёт положения плоскости H относительно точки А1; lH/ – отсчёт
положения плоскости H/ относительно точки А2 .
Точка на оси системы, в которой сходятся лучи, падающие на оптическую
систему параллельно оптической оси (т.е. точка с увеличением M = 0) и точка,
выйдя из которой лучи после прохождения оптической системы становятся
параллельными оптической оси (т.е. с увеличением M = ), называются
фокусами оптической системы. Плоскости, проходящие через фокусы
перпендикулярно оптической оси, называются фокальными.
n2/ c
M 0 lF /
;
a
nb
M lF 1 ,
a
где lF – отсчёт положения переднего фокуса
относительно точки А1 , lF/ – отсчёт положения
заднего фокуса относительно точки А2 .
110. Кардинальные элементы оптической системы
Расстояние f между передней главной точкой и передним фокусом называетсяпередним фокусным расстоянием; расстояние f / между задней главной
точкой и задним фокусом называется задним фокусным расстоянием:
n1
f lF lH ;
a
n2/
f lF / lH /
a
/
Главные и фокальные плоскости называются
элементами оптической системы.
кардинальными
111. Уравнение линзы
Уравнение линзы в форме Ньютона:zz ff
Уравнение линзы в форме Гаусса:
f/ f
1
/
s
s
/
/
112. Тонкие линзы
1 1 (n12 1)1
(n12 1)
/
n12 r1r2
f
r1 r2
1 1
1
(n12 1)
/
f
r1 r2
Тонкой линзой называется линза, для которых можно пренебречь третьим
слагаемым в скобках, что соответствует малости толщины линзы по сравнению
с каждым радиусом кривизны:
1 1 f /
S 21
1
0
n2/
n
Ф / 1
f
f
1
S
0
Оптическая сила линзы
1
1
1
0
1
f2
f1
d 1
1
0
1
113. Аберрации оптических систем
Отклонения фактически получаемого изображения от идеального, описываемоговсеми предыдущими формулами, называются аберрациями.
Аберрации
Геометрические
(монохроматические)
Основные виды:
• Сферическая аберрация
• Кома
• Астигматизм
• Искривление поверхности
изображения (кривизна поля)
• Дисторсия
Хроматические
Основные виды:
• Хроматизм положения
• Сферохроматическая
аберрация
• Хроматизм увеличения
114. Сферическая аберрация
Лучи, вышедшие из осевой точки предмета, после преломления (отражения) в ОС не собираются водну точку, а пересекают ОО в различных точках. Сферическая аберрация рассматривается в
меридиональной плоскости и определяется для пучков, исходящих из осевой точки.
Исходные диафрагмы
Распределение пучка в области
параксиального изображения
Распределение пучка в области
реального изображения
115. Кома
Кома – нарушение симметрии в структуре наклонного пучка впространстве изображений. Кома проявляется в нерезкости изображения
точки, характеризующейся несимметричностью пятна рассеяния относительно
сагиттальной плоскости.
Кома – аберрация широкого пучка лучей. Основная причина комы –
так же, как и для сферической аберрации – кривизна поверхности, но в
наклонном пучке отсутствует симметрия в условиях преломления или
отражения.
116. Астигматизм
Явление астигматизма заключается в том, что лучи бесконечно узкого наклонного пучка, идущиевблизи главного луча в меридиональной и сагиттальной плоскостях, после преломления в ОС не
собираются в одну точку: лучи, идущие в меридиональной плоскости, собираются в одну точку, а
лучи, идущие в сагиттальной плоскости – в другую.
Исходный предмет
Изображение
в сагиттальной плоскости
Изображение
в меридиональной плоскости
117. Кривизна поля
Поверхности, на которых лежат фокусы (где образуются отрезкилиний при астигматизме), создаваемые меридианальной и сагиттальной
фокусировками, не совпадают между собой и не являются плоскостями. Эти
поверхности касаются лишь в точке F/ оптической оси. Этот вид аберрации
называется искривлением поверхности изображения (кривизной поля).
118. Дисторсия
Увеличение системы, вообще говоря, зависит от угла наклона падающихлучей. В результате, например, сетка из прямых линий превращается в сетку
из кривых линий. Такая аберрация называется дисторсией .
Бочкообразная
дисторсия
Подушкообразная
дисторсия
119. Глаз как оптическая система
Фокусировка глаза на предметназывается аккомодацией
Средние характеристики человеческого глаза:
Оптическая сила
~ 58 дптр.
Длина глаза
~ 22 мм.
Радиус кривизны
сетчатки
~ 9,7 мм;
преломляющей
поверхности
~ 5,6 мм.
Показатель преломления
среды
1,33;
хрусталика
~ 1,4 – 1,45.
Расстояние наилучшего зрения
25 см.
120. Линзовый телескоп
Система КеплераСистема Галилея
Увеличение
f1
M .
f2
121. Лупа
Предмет располагается на расстоянии от лупы меньше фокусного.Изображение мнимое, прямое, увеличенное.
D
Увеличение M
f
D – расстояние наилучшего зрения (25 см)
122. Микроскоп
DdM
f1 f 2
123. Тема 6 Интерференция света
124. Интерференция света
Под интерференцией света обычно понимают широкий круг явлений, вкоторых при наложении световых волн результирующая интенсивность не
равна сумме интенсивностей отдельных волн: в одних местах она больше, в
других – меньше, т.е. возникают чередующиеся светлые и темные участки –
интерференционные полосы.
Другими словами, интерференцией называется изменение средней
плотности потока энергии, обусловленное суперпозицией электромагнитных
волн.
В дальнейшем под интенсивностью световой монохроматической волны
будем понимать следующую величину (без учета размерного коэффициента):
1
1
I Re E Re E Re( E E ) E02 ,
2
2
где E0 – действительная амплитуда световой волны.
125. Интерференция света
Рассмотрим суперпозицию двух линейно поляризованных в одном направленииволн с различными амплитудами:
E1 E01 exp i( t 1 ) ;
E2 E02 exp i( t 2 ) ;
E E1 E2 .
Тогда суммарная интенсивность будет равна:
1
I Re( E1 E2 )Re( E1 E2 ) Re ( E1 E2 )( E1 E2 )
2
Интерференционный
1
*
*
*
*
Re E1 E1 E2 E2 E1 E2 E2 E1 .
член
2
1 2
2
I E01
E02
2 E01 E02 cos I1 I 2 2 I1 I 2 cos ,
2
2
I1 E01
2,
2
I 2 E02
2,
2 1 .
Для волн с разными частотами: I I1 I2 2 I1 I2 cos 2 1 2 1 t
Суммарная интенсивность изменяется от минимального значения
I min
до максимального значения
I I
2
2
I max
1
2
I1 I 2
при cos 1
при cos 1 .
126. Интерференция света
Экспериментальные способы полученияинтерференционной картины
Способы деления амплитуды волны
Способы деления фронта волны
•Интерферометр Майкельсона
•Интерферометр Тваймана-Грина
•Интерферометр Маха-Цендера
•Интерферометр Фабри-Перо
•Опыт Юнга
•Бипризма Френеля
•Бизеркала Френеля
•Билинза Бийе
•Зеркало Ллойда
127. Интерферометр Майкельсона
I 2I0 1 cos 2 1I0 – интенсивность каждой из
интерферирующих волн.
2 1 2k l2 l1
Продольный эффект Доплера
u
0 1
c
u
I u, t 2 I 0 1 cos 2 1 t
c
Функция видности
V
I max I min
I max I min
128.
Интерферометр Тваймана -ГринаИнтерферометр Маха-Цендера
129. Опыт Юнга
Разность хода:2
d
d
l y l2 y
2
2
2
d
2
y
d
2
l 2 y l 1
2
2l 2
При d<<l
yd
l
d
C точностью до величины первого порядка по
l
k
Разность фаз между волнами в точке наблюдения:
2
2 d
y
l
2 I0 1 cos
.Интерференционная картина на экране в зависимости от координатыIy: y
Ширина интерференционной полосы
y
2
2
l
d
2 d
y
l
130. Примеры интерференционных схем (метод деления фронта)
Бипризма ФренеляБизеркала Френеля
Билинза Бийе
Зеркало Ллойда
131. Когерентность света
Когерентность света - взаимная согласованность протекания во временисветовых колебаний в разных точках пространства и (или) времени,
характеризующая их способность к интерференции.
При описании интерференционных явлений часто используют понятия
временной и пространственной когерентности.
Временную
когерентность
обычно
связывают
со
степенью
монохроматичности волн (например, в интерферометре Майкельсона при
рассмотрении осевых пучков), а пространственную когерентность – с
геометрией эксперимента (как в опыте Юнга или при рассмотрении
интерференции от протяженных источников света).
132. Временная когерентность
i – средние времена сменыфазы колебания амплитуды.
N
i
ког i 1
N
Время когерентности
lког c ког
Длина когерентности
Размывание полос интерференции в интерферометре Майкельсона
обусловлено конечностью времени и длины когерентности света, т.е.
обусловлено временной когерентностью.
133. Пространственная когерентность
Пусть задан протяженный источник света с шириной b. 2 –угловая апертура интерференции. В направлении 1
положение каждой точки в пределах b роли не играет. При
распространении под углом к этому направлению положение
каждого точечного источника обуславливает дополнительную
разность хода. Максимальная разность хода достигается между
направлениями 1 и 2 или 1 и 3:
AD BC b sin
/2
- интерференционная картина исчезает.
Интерференционная картина становится достаточно
четкой, если смещение интерференционных картин,
полученных от крайних точек A и B протяженного
источника, не превышает половины полосы:
bsin
4
Условие
пространственной когерентности
При дальнейшем уменьшении размеров источника его можно считать практически точечным.
134.
Виды интерференционных полос= const; = const. При вариации геометрической разности
хода имеют место полосы равной толщины.
= const; = const. При вариации угла падения получаем
полосы равного наклона.
= const; = const. При вариации длины волны получаем
полосы равного хроматического порядка.
135. Полосы равного наклона
Оптическая разность хода:AB BC n AE
2
2
2 nh cos
Условие максимумов
m ,
m 0,1,2,3,
Условие минимумов
(2m 1) ,
2
m 0,1,2,3,
136. Полосы равной толщины
2 nh cos2
Кольца Ньютона
Радиус m-го темного кольца:
rm R m
137. Многолучевая интерференция (интерферометр Фабри-Перо)
R R;2
2
R R ;
TT 1 ,
где и – энергетические
коэффициенты
пропускания и отражения
Разность хода между соседними
интерферирующими волнами на выходе
пластины равна
Разность фаз:
E2 E0TT 1 R e
2
i
R e
4
i 2
2nh cos
k 2nkh cos
R' 1
E0TT '
N 1 R'2 exp i
138. Многолучевая интерференция (интерферометр Фабри-Перо)
I2I0 1
1
4
1
2
sin
2
Формула Эйри
2
I2/Io
1,0
1
0,5
2
3
0,0
2 m
2 (m+1)
139. Разрешающая способность и дисперсионная область ИФП
Пусть на ИФП падают две волны с близкими длинами и + . Каждая из нихсоздает свою интерференционную картину. При достаточно близких длинах волн
возникает проблема разрешения (различения) этих двух длин волн по
наложенным интерференционным картинам. Разрешающая способность
интерферометра характеризуется минимальной разницей в длинах волн,
при которой возможно их разрешение:
Для ИФП:
2 h
1
Разность длин волн, при которой наступает перекрытие полос соседних
порядков интерференции, называется дисперсионной областью (или
областью свободной дисперсии) G. Из определения дисперсионной
области следует:
m 1 m G
G
m
2
2h
0 m
G
2h
140. Применения многолучевой интерференции
•Спектроскопия•Лазерные резонаторы
•Просветление оптики
•Интерференционные зеркала
•Микро- и наноструктурные оптические
волокна
141. Тема 7 Дифракция света
142. Принцип Гюйгенса-Френеля
Пусть A – источник света, а – произвольная замкнутаяповерхность, охватывающая A (см. рис.).
Принцип Гюйгенса – Френеля: в любой точке,
находящейся вне поверхности , световая волна,
возбуждаемая источником A, может быть представлена
как результат суперпозиции когерентных вторичных волн,
которые “излучаются” элементарными воображаемыми
источниками, непрерывно распределенными вдоль
вспомогательной поверхности .
exp ikr
EP K ( ) E (r1 )
d .
r
143. Зоны Френеля
M1 P DP 2 ;M 2 P M1 P 2 ;
...................
M m P M m 1 P 2 .
2
rm2 R 2
R d m L m 1 L d m 2 .
2
2
Пренебрегая слагаемыми 2 ввиду их малости, получаем:
RL(m 1)
2
rm
.
R L
RL
Sm
.
R L
Радиус m-й зоны Френеля
Площадь зоны Френеля
144. Метод векторных диаграмм
iE P E0 E0 e E0 e
i 2
... .
Пятно Пуассона
145. Зонная пластинка Линза Френеля
Пусть лучи падают на зонную пластинку параллельно оси системы, т.е. R = . Тогдаточка P является фокусом.
2
rm (m 1) L .
Фокусное расстояние:
1 1 1
.
R L f
rm2
f L
.
(m 1)
В отличие от обычной линзы зонная пластинка имеет
несколько фокусов на оси системы в зависимости от
количества открытых зон.
146. Дифракция Френеля Дифракция Фраунгофера
2N
1
L
Дифракция Френеля (дифракция в ближней зоне)
2
N
1
L
Дифракция Фраунгофера (дифракция в дальней зоне)
– характерный размер препятствия; L – расстояние между дифракционным
экраном и экраном наблюдения.
Дифракция Френеля - дифракция сферической световой волны на
неоднородности (например, отверстии), размер которой сравним с диаметром
одной из зон Френеля
Дифракция Фраунгофера - дифракция слабо расходящегося (практически
параллельного) пучка лучей света на неоднородности (например, отверстии),
размер которой много меньше диаметра первой из зон Френеля.
ik xx / yy / / /
Ф( x, y) x , y exp
dx dy
l
S/
/
/
147. Дифракция на прямоугольном отверстии
kax;
2l
kby
2l
a/2
ikxx / / b / 2
ikyy / /
A0
sin sin
A x, y
exp
dx exp
dy A0
ab a / 2
l b / 2
l
a
I x , y A0
2
sin
2 sin
2
148. Дифракция на щели
E0 d xd E
exp i t kx sin .
b
b
E0
E1 d E1
exp i t exp ikx sin d x.
b
0
kb
b
u sin
sin
2
2
sin u
I I0
,
u
1. В центре дифракционной картины интенсивность
максимальна и равна I0
2. При углах , для которых sinu = 0, а u 0, интенсивность света
обращается в нуль. Условие минимума дифракционной картины на
одиночной щели:
b sin n ,
3.
4.
n 1, 2, 3, ...
Основная часть потока энергии сосредоточена в пределах
изменения угла дифракции между первыми (n = 1)
симметричными максимумами.
Чем меньше (уже) щель, тем шире центральный максимум. При b
центральный максимум расплывается на всю
полуплоскость ( /2). Дальнейшее уменьшение щели
приводит лишь к монотонному уменьшению интенсивности
прошедшего света.
I1
I0
0
149. Дифракция на круглом отверстии
R2
/
A0
/r
/
/
/
A r ,
r exp ikr cos d dr
2
l
R 0
2J1( /
R
2 A0 / krr / /
dr ,
2 r J 0
R 0
l
xJ 0 x dx xJ1 x
0
I1
2 J1 kRr / l
A r A0
.
kRr / l
I0
0
Угловой размер центрального светлого
пятна (диска Эйри), наблюдаемого из
центра круглого отверстия:
0 1,22
R
150. Дифракция на прямолинейном крае экрана
/2/ 2
x
y
dx / dy / ~
E ~ exp ik l
2l
x
2
l
y / 2 / x
x / 2 /
~ exp ik
dy exp ik
dx ~
2
l
2
l
0
/ 2 /
~ exp i
d ,
2
0
X cos / 2 d ; Y sin / 2 d /
/2
/
0
Спираль Корню
(клотоида)
0
/2
151. Дифракционная решетка
ukb
b
sin
sin
2
d
sin .
2
2
sin u sin N
I I0
.
u sin
I
sin
d sin m , m 0,1,2,3,...
Условие главных максимумов
b sin n , n 1, 2, 3, ...
Условие минимумов огибающей
152. Разрешающая способность и дисперсионная область дифракционной решетки
Критерий Рэлея: две спектральные линии являются разрешенными, еслимаксимум дифракционной картины для одной длины волны совпадает с
ближайшим минимумом для другой длины волны.
d sin 1max m 1;
1
d
sin
m
2 ;
2min
N
1max 2min .
mN
G
m
153. Тема 8 Основы голографии
154. Голография
Голографией называют метод записи и последующеговосстановления пространственной структуры световых
волн, основанный на явлениях интерференции и
дифракции когерентных пучков света.
Фотопластинка, на которой записана эта информация,
называется голограммой.
На
голограмме
регистрируется
не
оптическое
изображение объекта, а интерференционная картина,
возникающая при наложении световой волны, рассеянной
объектом (предметной волны), и когерентной с ней
опорной (или референтной) волны.
155. Запись голограмм
Схема записи тонкослойной голограммы156. Воспроизведение голограмм
Схема воспроизведения голограммы157.
Схема записи объемных голограмм158. Основные области применения голографии
•Запись и хранение информации, в т.ч. ивизуальной (оптическая голографическая
память)
•Оптическая обработка информации и системы
распознавания образов
•Голографическая интерферометрия
159. Тема 9 Распространение света в анизотропных средах
160. Оптическая анизотропия
Оптической анизотропией называется зависимостьоптических свойств среды от направления распространения
света в ней.
В анизотропной среде проекции поляризованности
проекциями напряженности электрического поля соотношениями:
Px 0 xx E x 0 xy E y 0 xz E z ;
Py 0 yx E x 0 yy E y 0 yz E z ;
связаны
с
Матрица величин ij называется
тензором диэлектрической
восприимчивости.
Pz 0 zx E x 0 zy E y 0 zz E z .
3
Pi 0 ij E j ;
i, j 1, 2, 3
j 1
Соотношение между компонентами вектора электрического смещения D и
поляризованностью P для анизотропной среды:
3
3
3
Di 0 Ei 0 ij E j 0 ( ij ij ) E j ij E j
j 1
j 1
ij o ( ij ij )
j 1
где ij – символ Кронекера.
тензор диэлектрической проницаемости
161. Свойства тензора диэлектрической проницаемости
Плотность электрической энергии:1 3 3
w E j ji Ei
2 j 1 i 1
1
1 3
1 3 3
w (E D) Ei Di Ei ij E j
2
2 i 1
2 i 1 j 1
1 3 3
0 ( ij ji ) Ei E j
2 i 1 j 1
Тензор диэлектрической проницаемости является симметричным:
Перейдем к новым переменным:
3
3
ij xi x j 1
i 1 j 1
xi
Ei
2w
x x2 y y2 z z 2 1
Уравнение описывает эллипсоид с полуосями,
расположенными вдоль главных осей тензора и
равными x-1/2, y-1/2, z-1/2. В главных осях:
x
ij 0
0
ij ji
0
y
0
Dx x E x ;
Dy y E y ;
Dz z E z .
Т.к. в общем случае элементы тензора диэлектрической проницаемости
неодинаковы, то в анизотропной среде векторы D и E не коллинеарны.
0
0 .
z
162. Структура световой волны в анизотропной среде
k H D ;k E H ;
0
k D 0 ;
k H 0 .
k
n
k
направление волны
S
S
направление луча
Плоскость равных фаз перемещается вдоль вектора n со скоростью v.
Скорость перемещения этой плоскости вдоль вектора луча называется
лучевой скоростью.
u v cos n, v n
Лишь при ориентации вдоль одной из главных осей кристалла
вектор D коллинеарен вектору E.
163. Зависимость фазовой скорости от направления распространения волны и плоскости поляризации
n n E E 0 v 2 D 0В главной системе координат:
ni n E Ei 1 v 2 0 i 0
(i 1, 2, 3)
ni – направляющие косинусы направления волны относительно
соответствующей главной оси.
vi
1
i 0
(i 1, 2, 3)
- главные скорости распространения волны.
1. vi – это не проекции вектора фазовой скорости на соответствующую главную
ось, а фазовые скорости волны, у которой векторы E и D коллинеарны
соответствующей главной оси;
2. Главные лучевые (групповые) скорости совпадают с главными фазовыми
скоростями.
164. Уравнение Френеля
ni20
2
2
i 1 v i v
уравнение Френеля для фазовых скоростей
i2 v i2
0
2
2
i 1 v i u
уравнение Френеля для лучевых скоростей
3
3
ni2
f (v ) 2
2
i 1 v i v
3
2
Векторы D двух волн с двумя различными скоростями v’ и v’’, которые могут
распространяться в данном направлении, взаимно перпендикулярны.
165. Эллипсоид лучевых скоростей
x2 y2 z 22 2 1
2
vx v y vz
vx, vy, vz – главные лучевые скорости. Эллипсоид, точки
поверхности которого удовлетворяют этому уравнению,
называется эллипсоидом лучевых скоростей
(координаты имеют размерность скоростей).
Направление, перпендикулярное круговому
сечению, называется оптической осью
анизотропной среды (кристалла). Для лучей,
идущих вдоль оптической оси среда ведет
себя как изотропная.
Эллипсоид с тремя различными полуосями (главными скоростями)
имеет два круговых сечения и, отсюда, две оптические оси. Такие кристаллы
называются двуосными. Если у эллипсоида лучевых скоростей любые две
главные скорости совпадаю по величине, то это эллипсоид вращения. Он
имеет лишь одно круговое сечение (и одну оптическую ось, совпадающую с
осью симметрии). Такие кристаллы называются одноосными. В случае
совпадения всех трех главных скоростей мы имеем изотропную среду.
166. Лучевая поверхность
Лучи в анизотропной среде можно рассматривать и без эллипсоида лучевыхскоростей непосредственно с помощью уравнения Френеля. Введем новые
переменные:
r u; ri xi i u
В этих переменных уравнение принимает вид:
xi2 v i2
r 2 v2 0
i 1
i
3
Это уравнение описывает поверхность четвертого порядка, называемое
лучевой поверхностью. Расстояние r от начала координат до
соответствующей точки поверхности пропорциональна лучевой скорости в
этом направлении . В каждом направлении лучевая поверхность встречается
два раза, что соответствует наличию двух скоростей распространения света в
данном направлении.
167. Двулучепреломление
Плоскость, проходящая через луч, направленный под углом к оптической оси иоптическую ось, называется главной.
У луча, вектор E0 которого направлен перпендикулярно главной плоскости,
скорость не зависит от направления и равна лучевой скорости, направленной
коллинеарно оптической оси. Такой луч называется обыкновенным.
У луча, вектор Eе которого лежит в главной плоскости, скорость зависит от
направления, т.к. соответствующая полуось эллипса в сечении эллипсоида
изменяется с изменением направления луча. Такой луч называется
необыкновенным.
Показатель преломления необыкновенного луча – величина переменная,
зависящая от направления луча. Значение ne, приводящееся для данного
кристалла в справочной литературе – это максимально отличающееся от
«обыкновенного» показателя преломления no значение.
v0 ve
отрицательные кристаллы
v0 > ve
положительные кристаллы
168. Сечения лучевых поверхностей
Т.к. внутри кристалла могут распространяться только два луча с различнымилучевыми скоростями, то преломление луча на границе с кристаллом приводит
в общем случае к возникновению двух лучей внутри кристалла. Такое явление
называется двулучепреломлением .
169. Построение Гюйгенса
Производится с помощью лучевыхповерхностей (рис. – для отрицательных
кристаллов). Лучевая поверхность строится в
AB 1
единицах
1/n.
Тогда
(здесь 1 – это показатель преломления
первой среды). Точки C и D – точки
пересечения касательных к лучевым
поверхностям, т.е. лучи OC и OD – нормали к
касательным.
170. Четвертьволновые и полуволновые пластины
Если луч падает нормально к поверхности кристалла, а оптическая осьпараллельна поверхности, то обыкновенный и необыкновенный лучи не
разделяются пространственно, а идут нормально поверхности раздела с
различными
скоростями.
На
выходе
такой
плоскопараллельной
кристаллической пластины толщиной d волны приобретают разность фаз:
2
2
no ne d
Если вектор E в падающей линейно поляризованной волне ориентирован под
углом 45o к главной плоскости и параметры пластины и
/4
/2
- вышедший свет будет иметь круговую поляризацию. Такая
пластинка называется четвертьволновой;
- на выходе – линейно поляризованная волна с ориентацией
вектора E под 90о к ориентации поля E в падающей волне
(полуволновая пластинка);
- поляризация волны не меняется (пластина в целую длину волны).
171. Компенсаторы
no ne d1 ne no d 2 no ne d1 d 2172. Поляризационные и двоякопреломляющие призмы
Призма называется поляризационной, когда на ее выходе имеется однаполяризованная волна, а двоякопреломляющей, если на выходе имеются обе
ортогонально поляризованные волны.








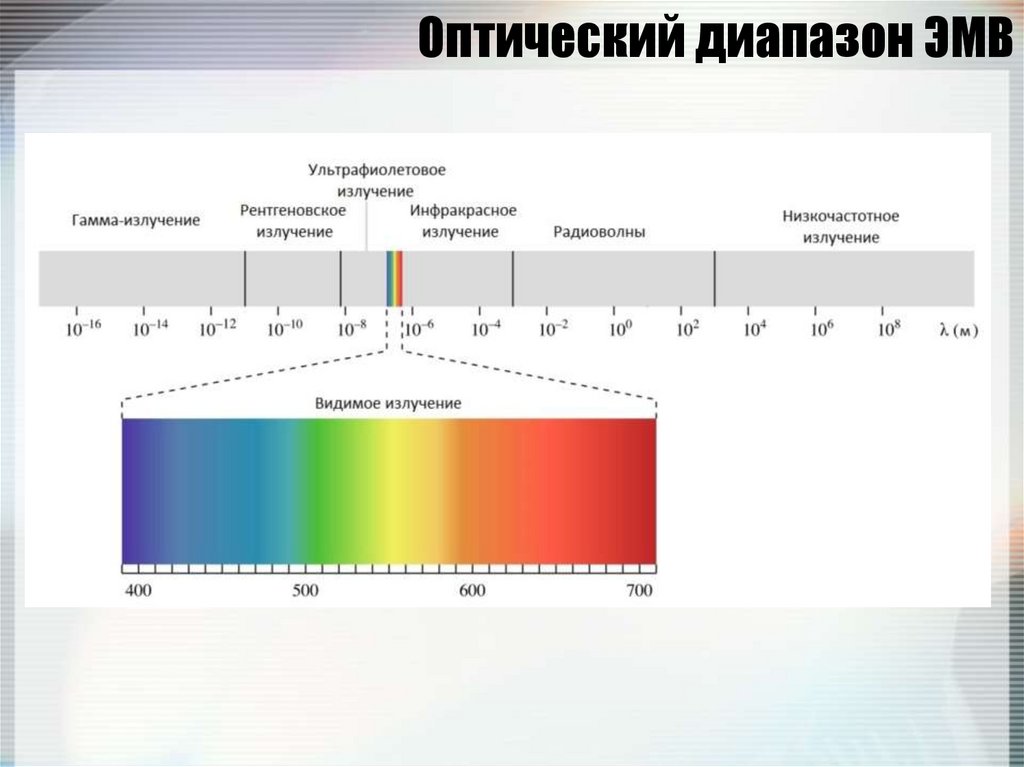

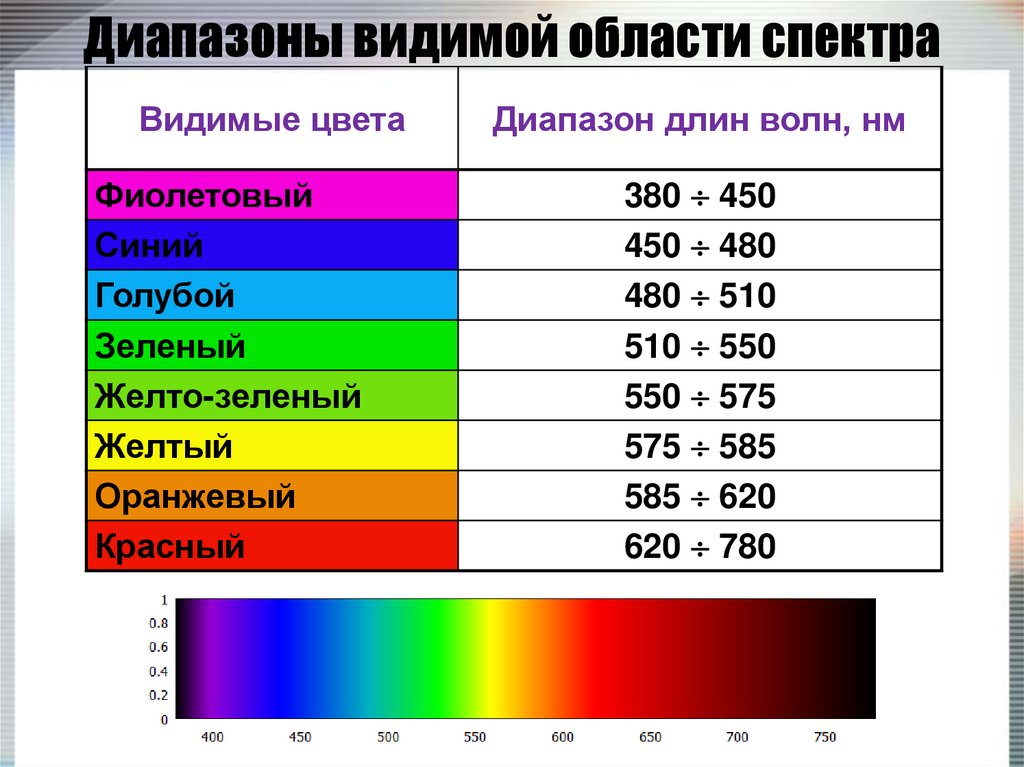














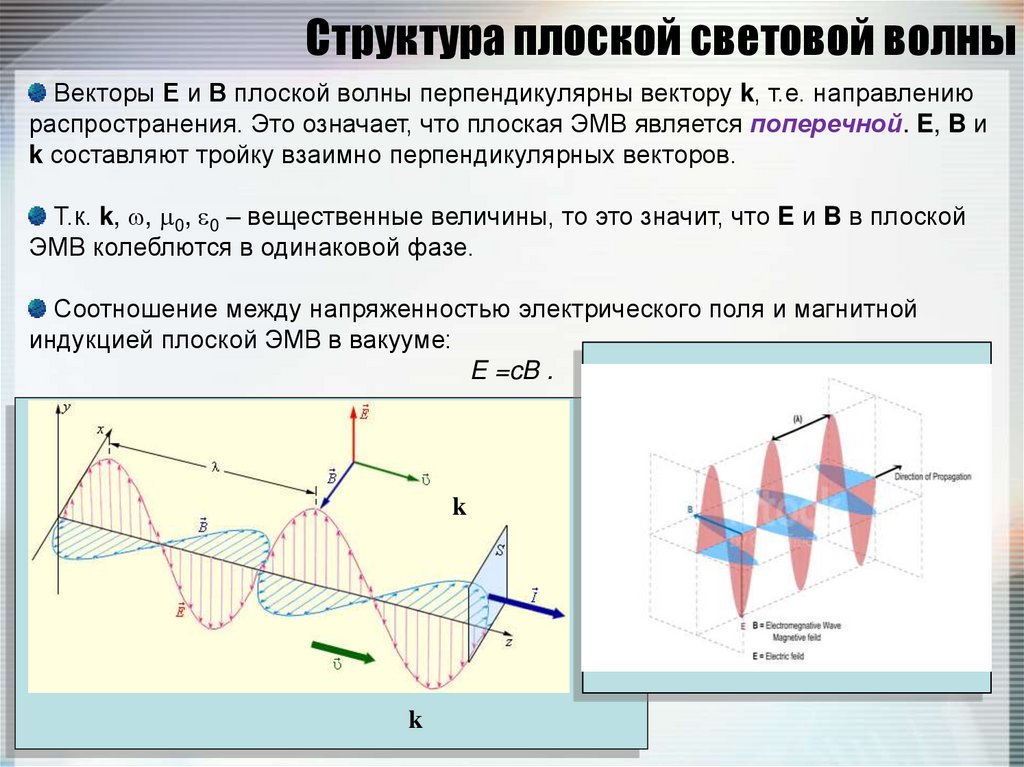

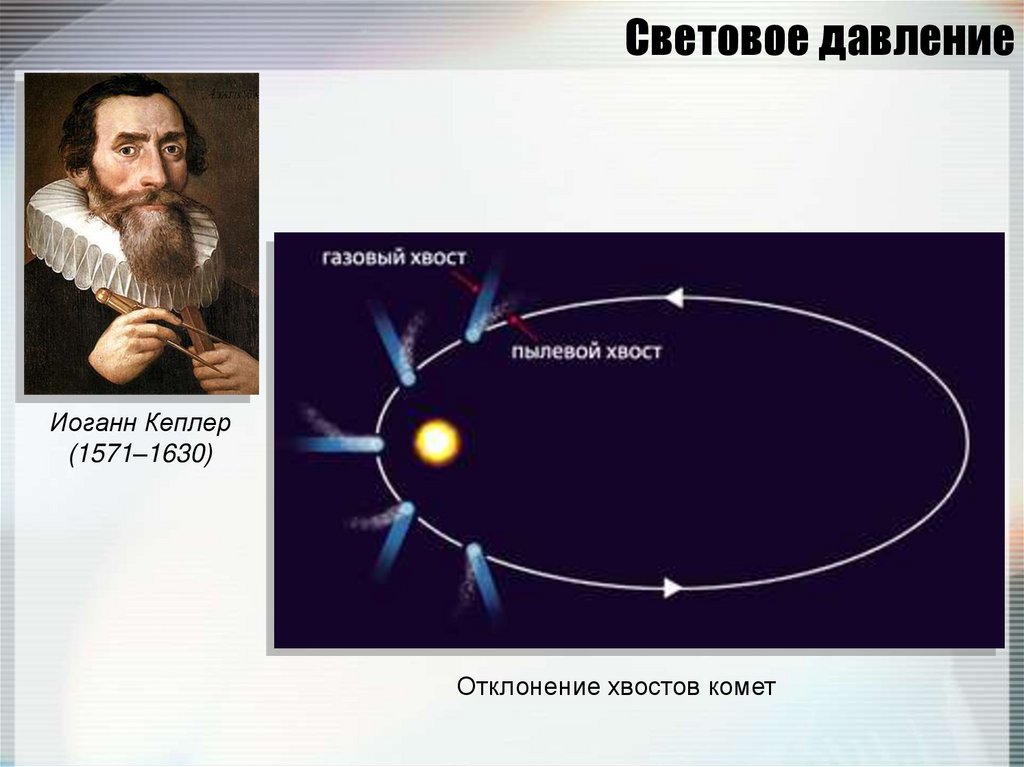



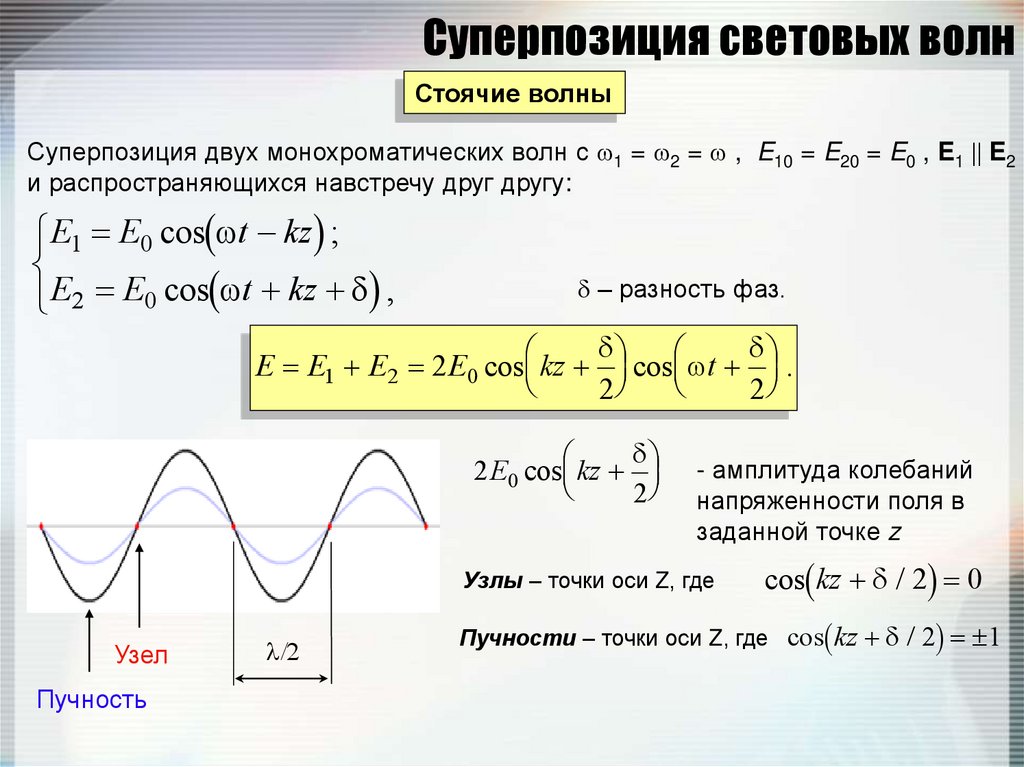


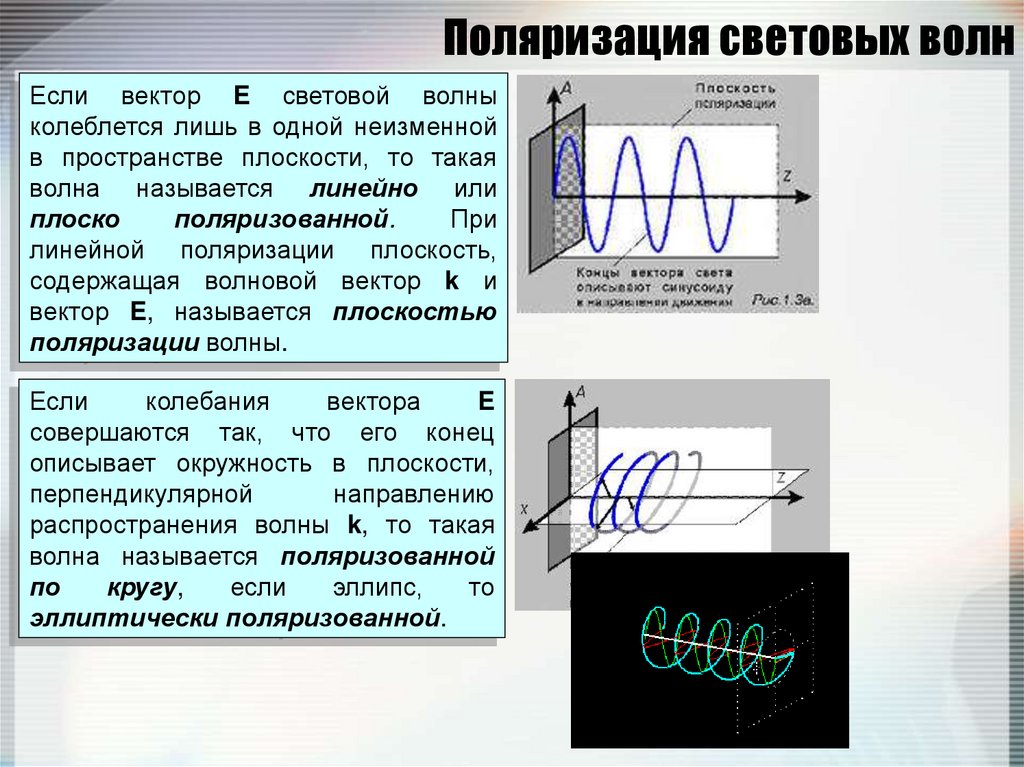

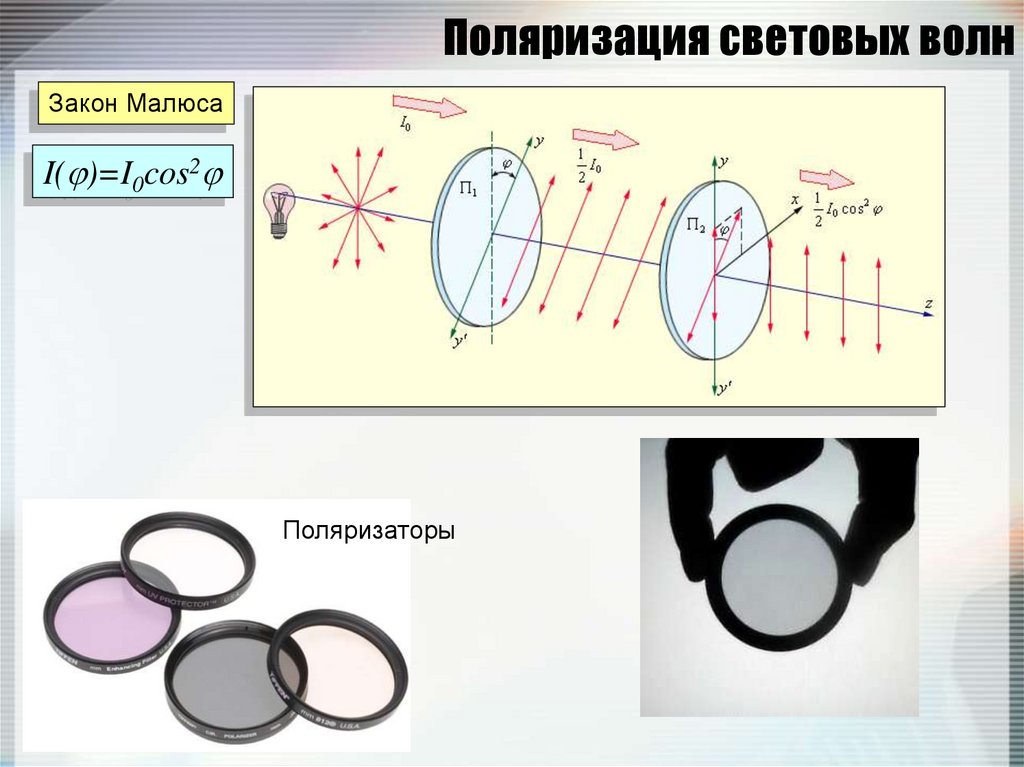













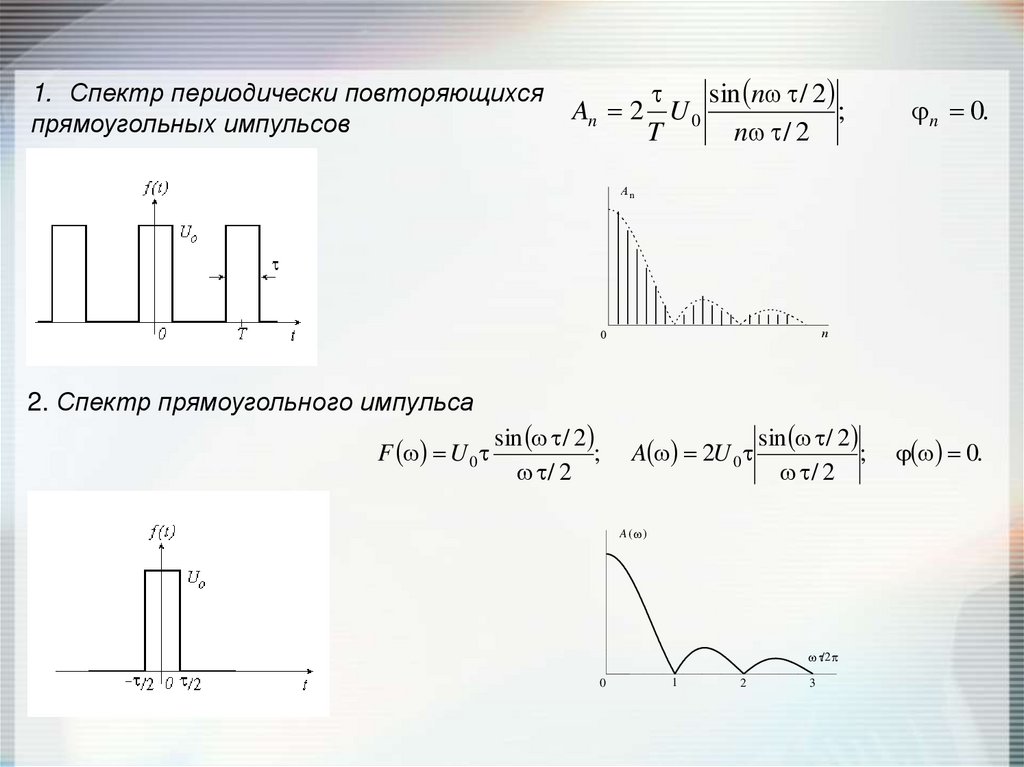














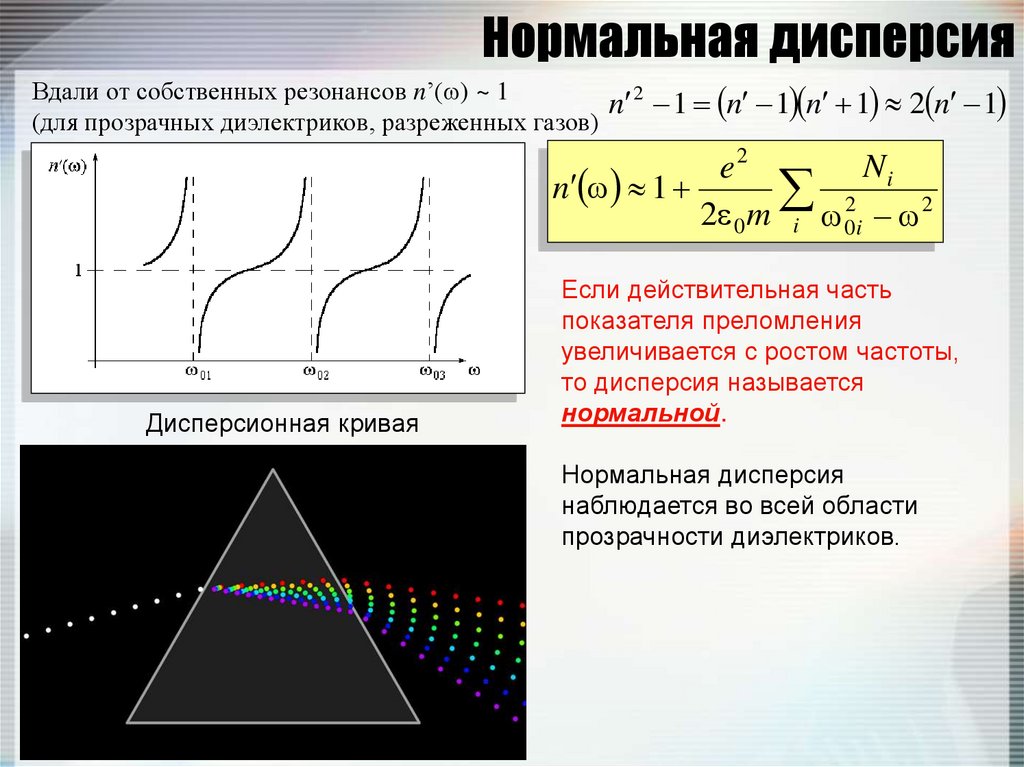
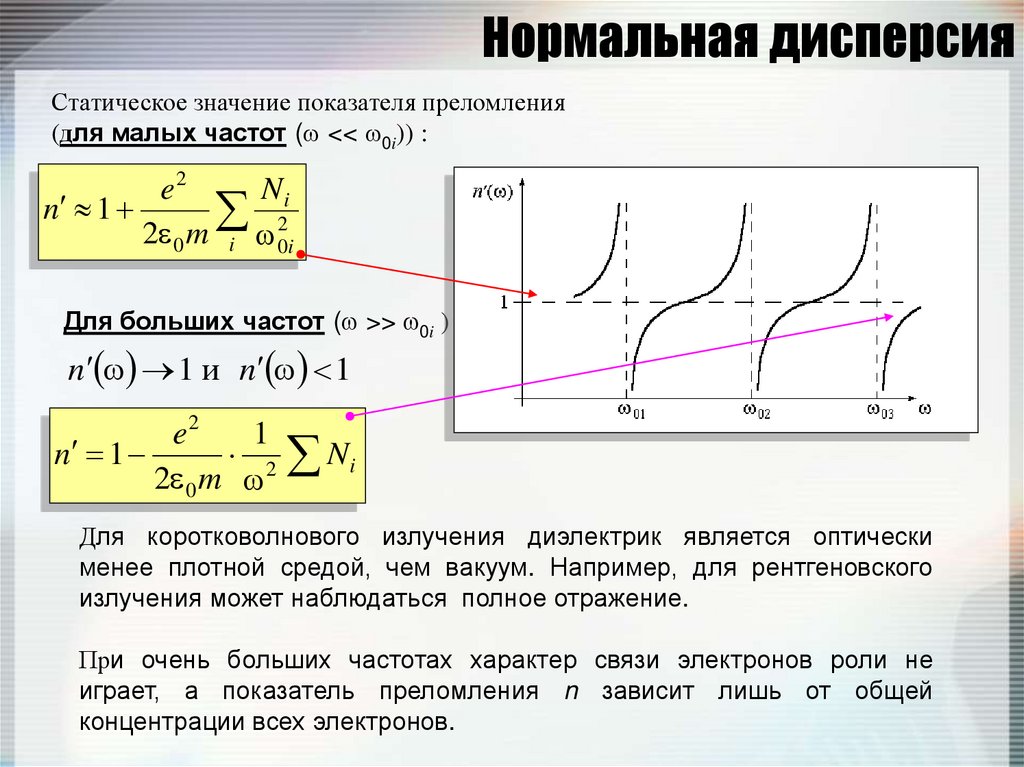
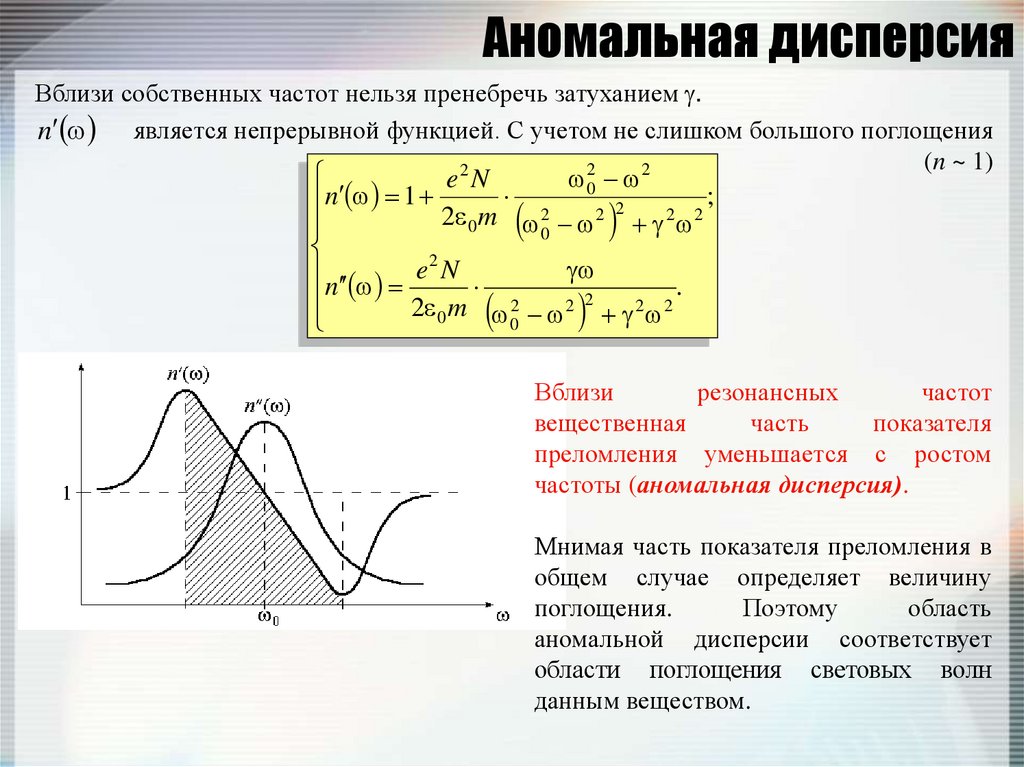


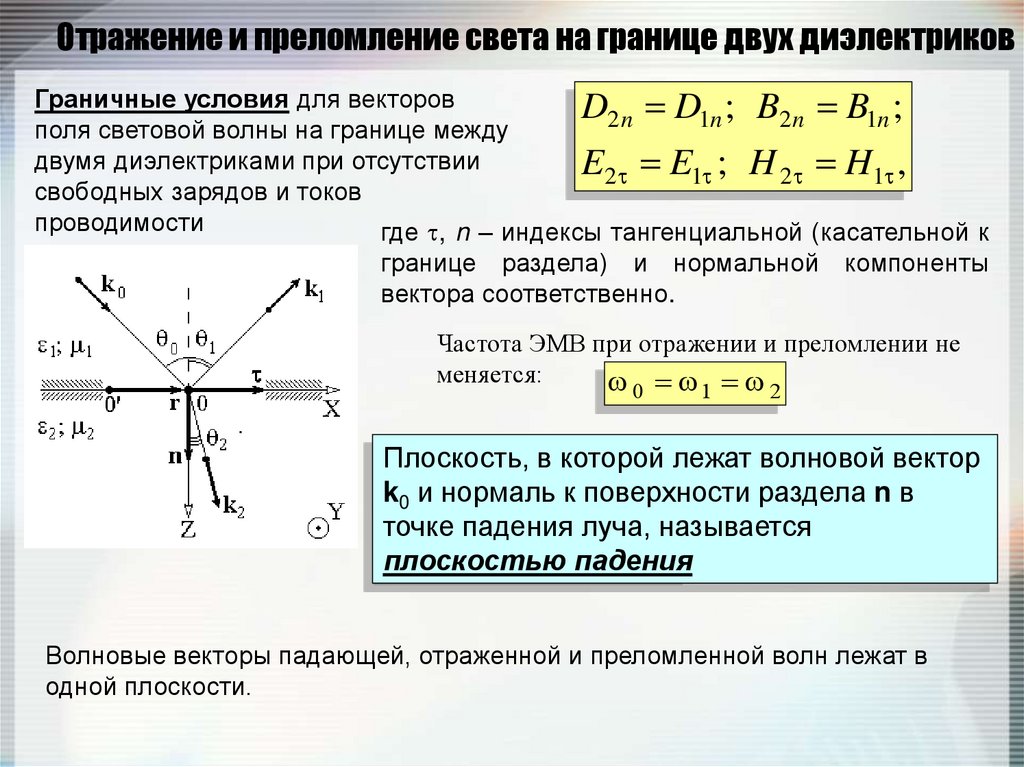
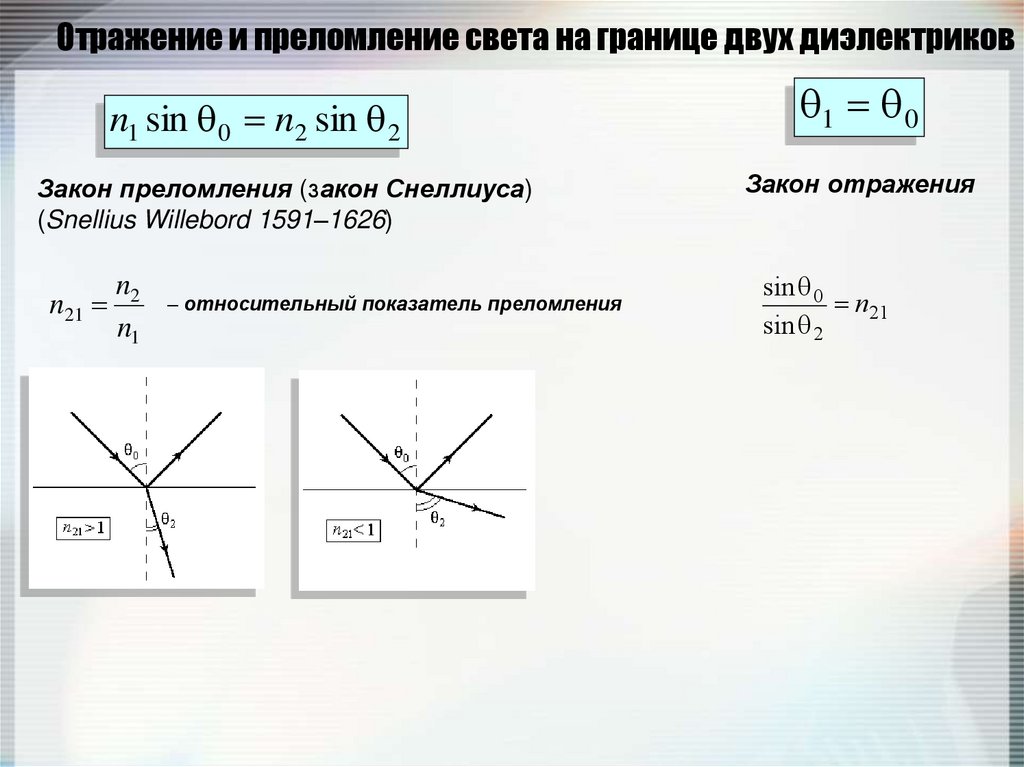





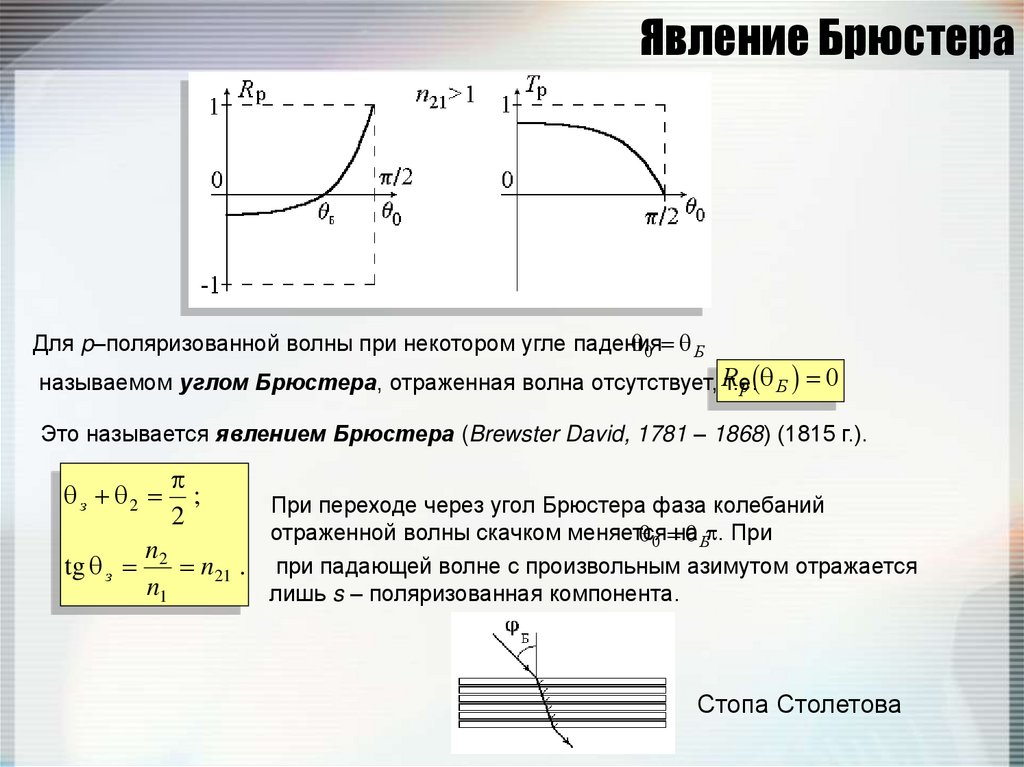


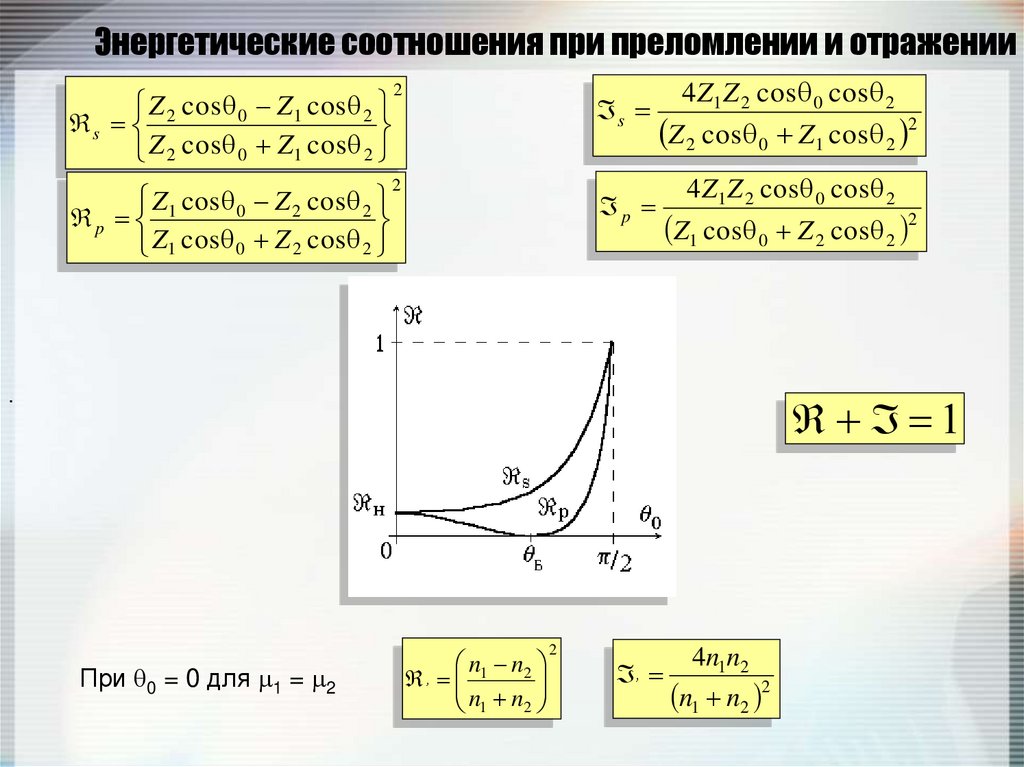



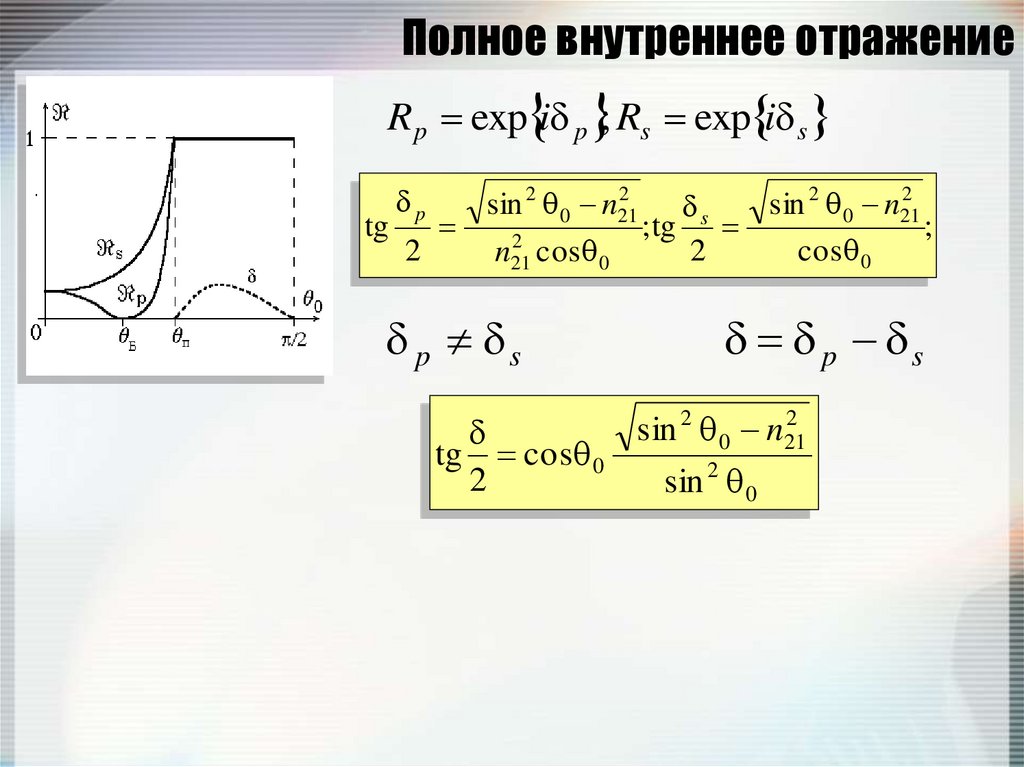
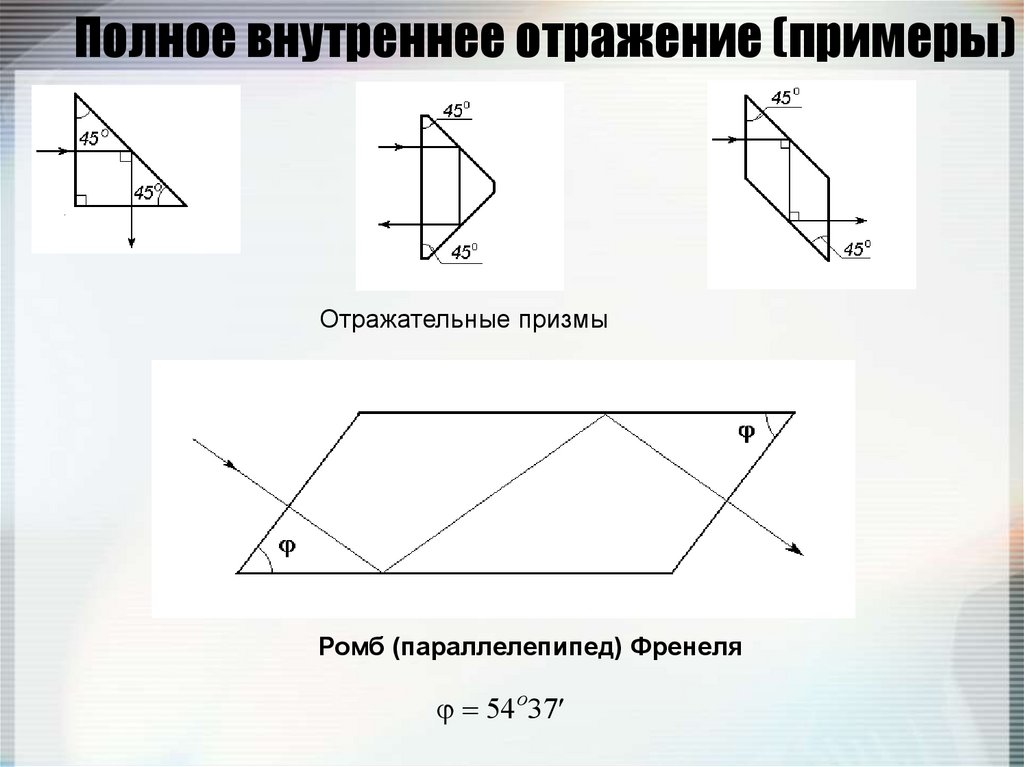




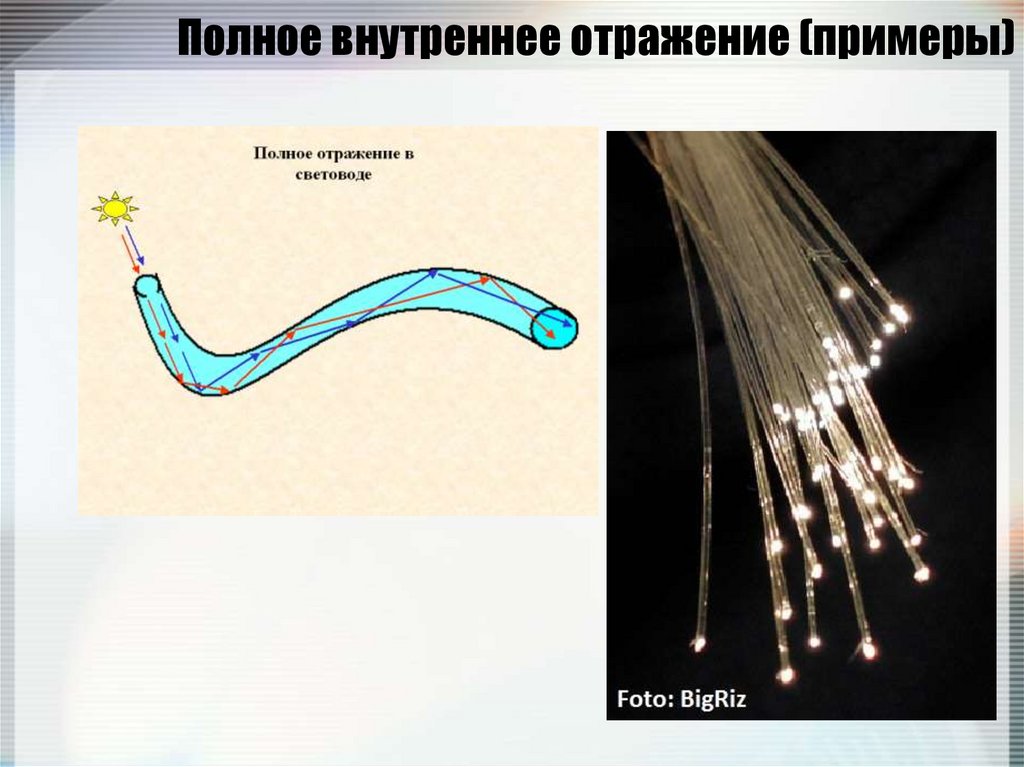

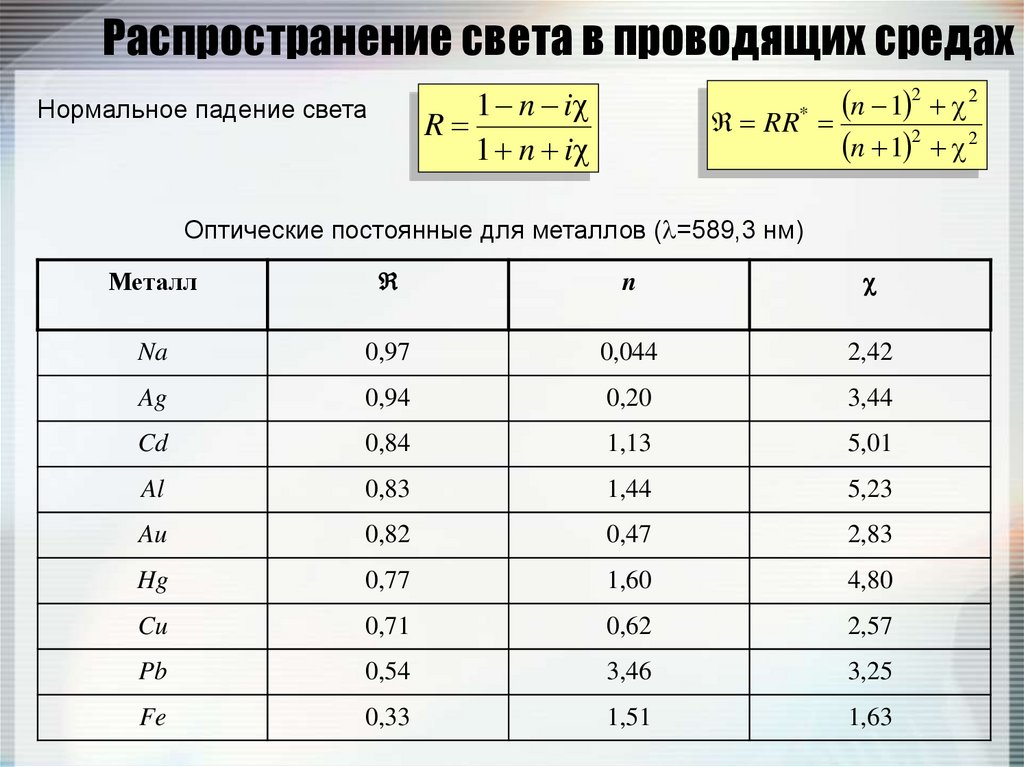









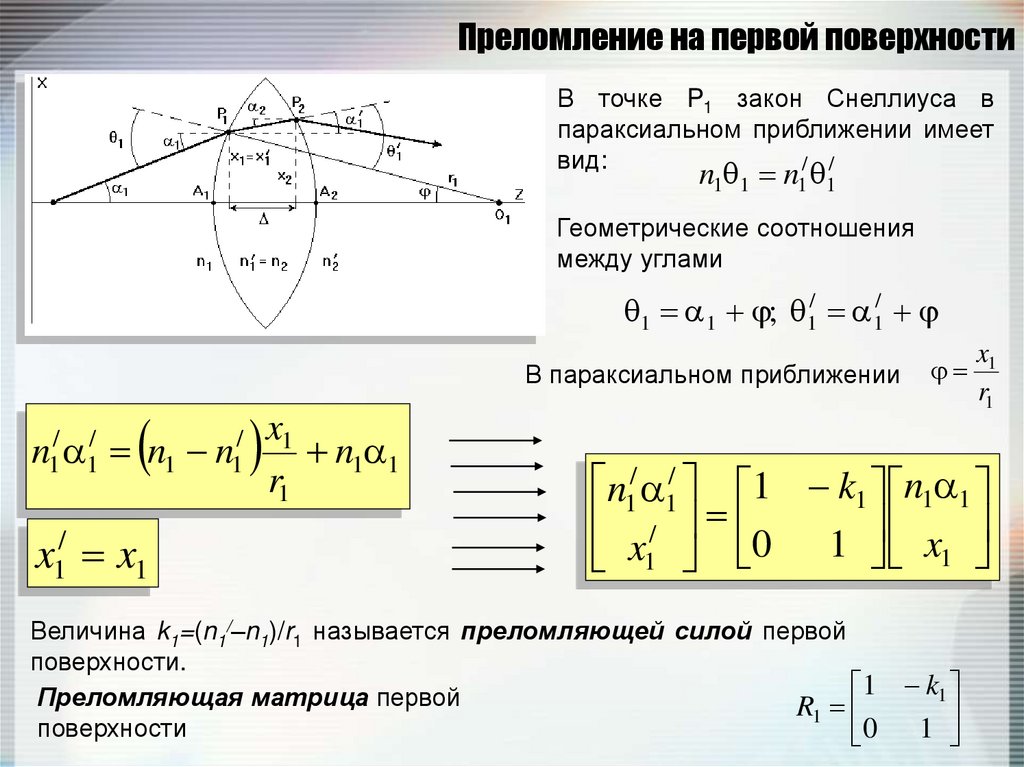
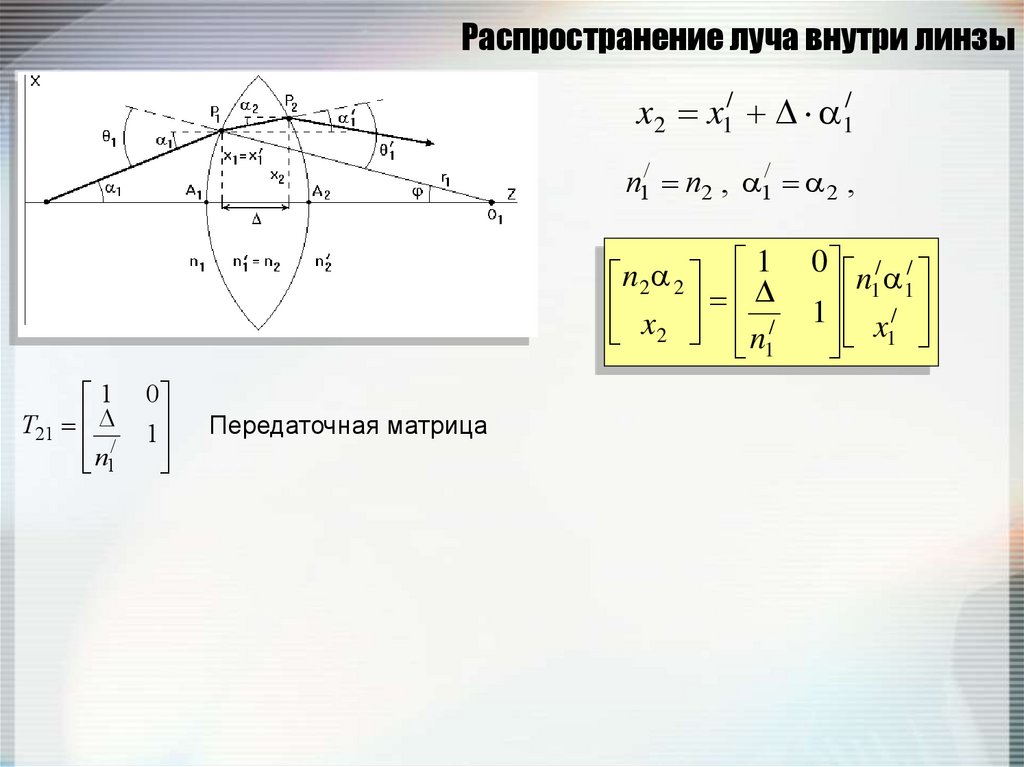






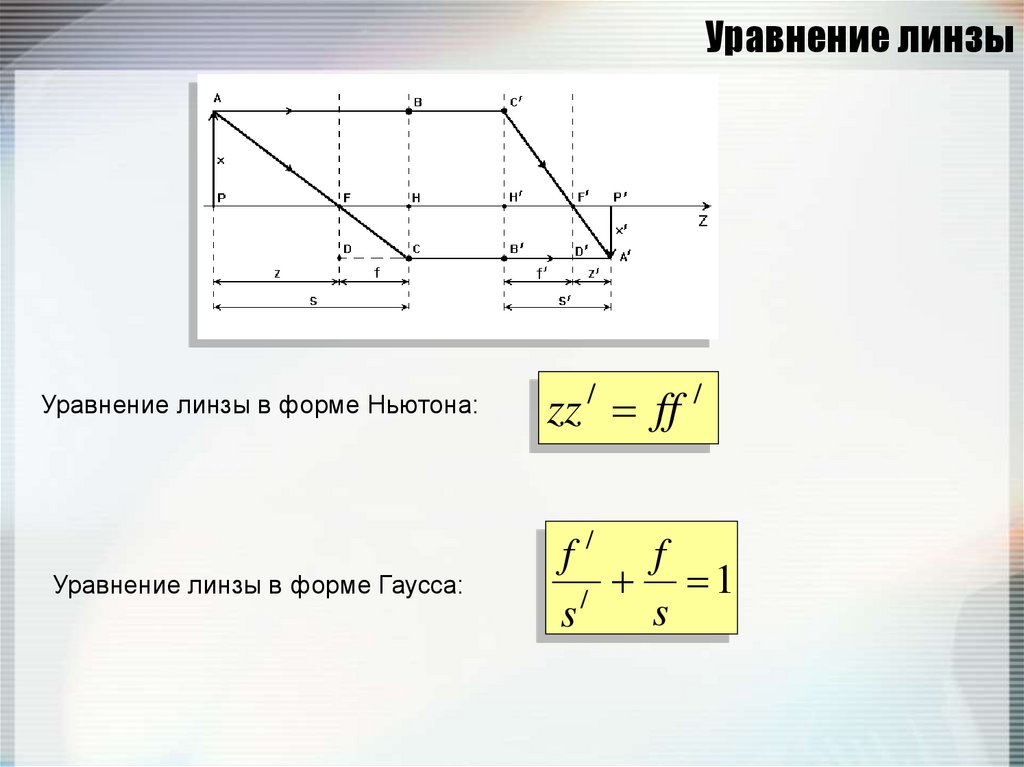

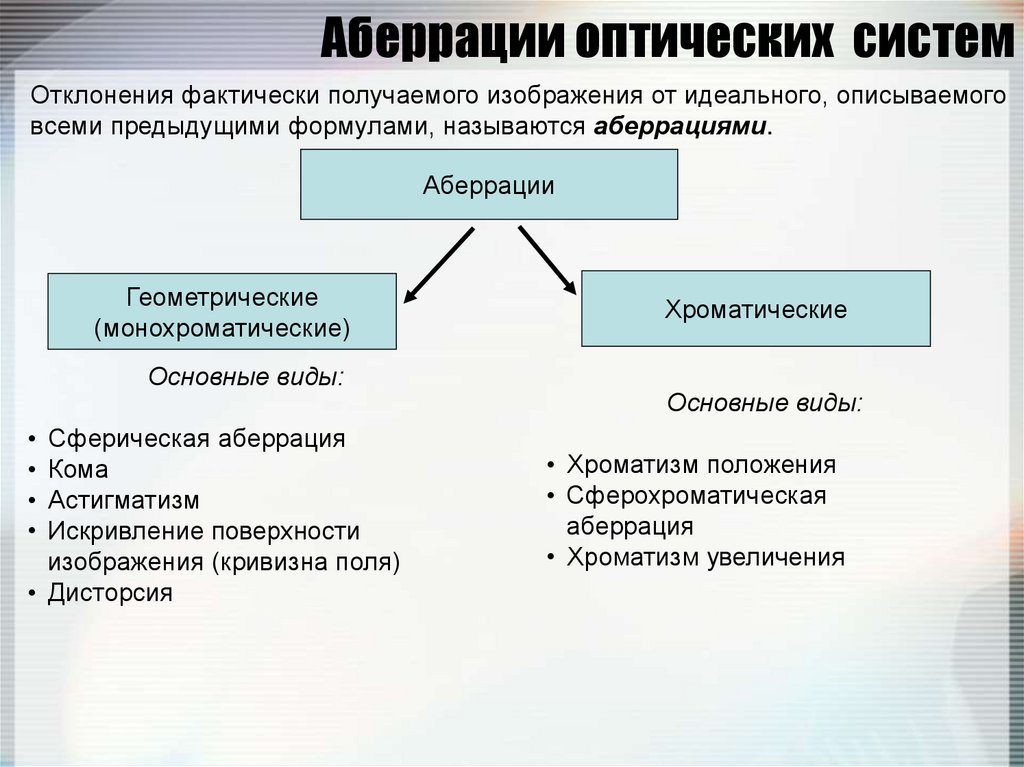
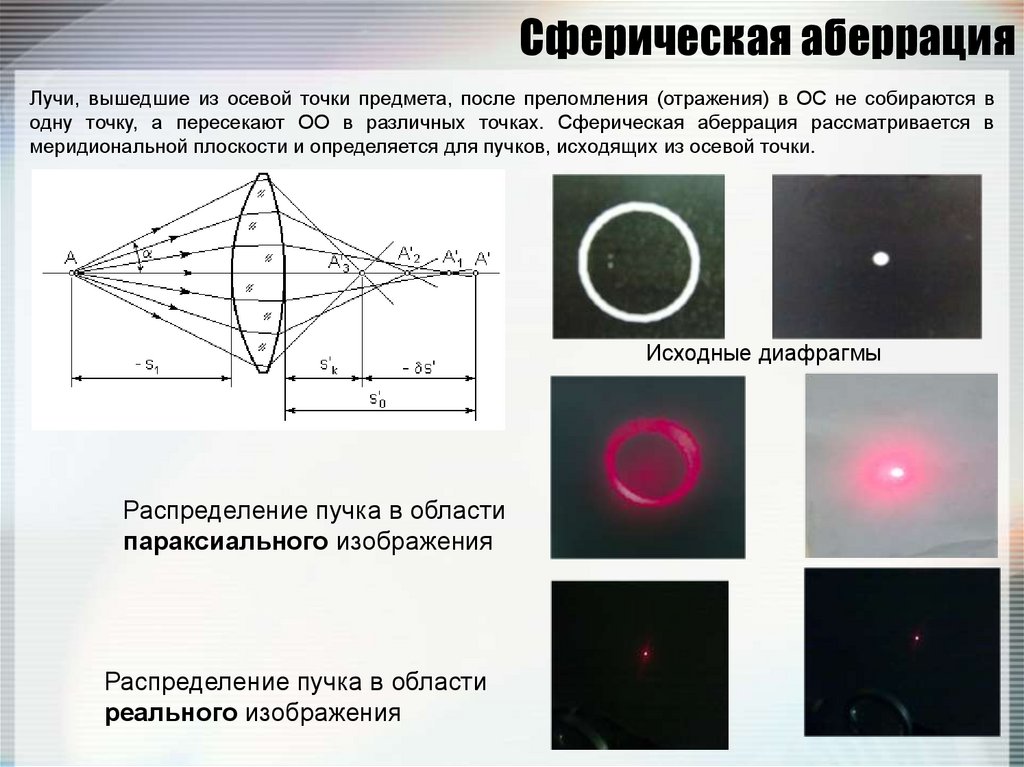


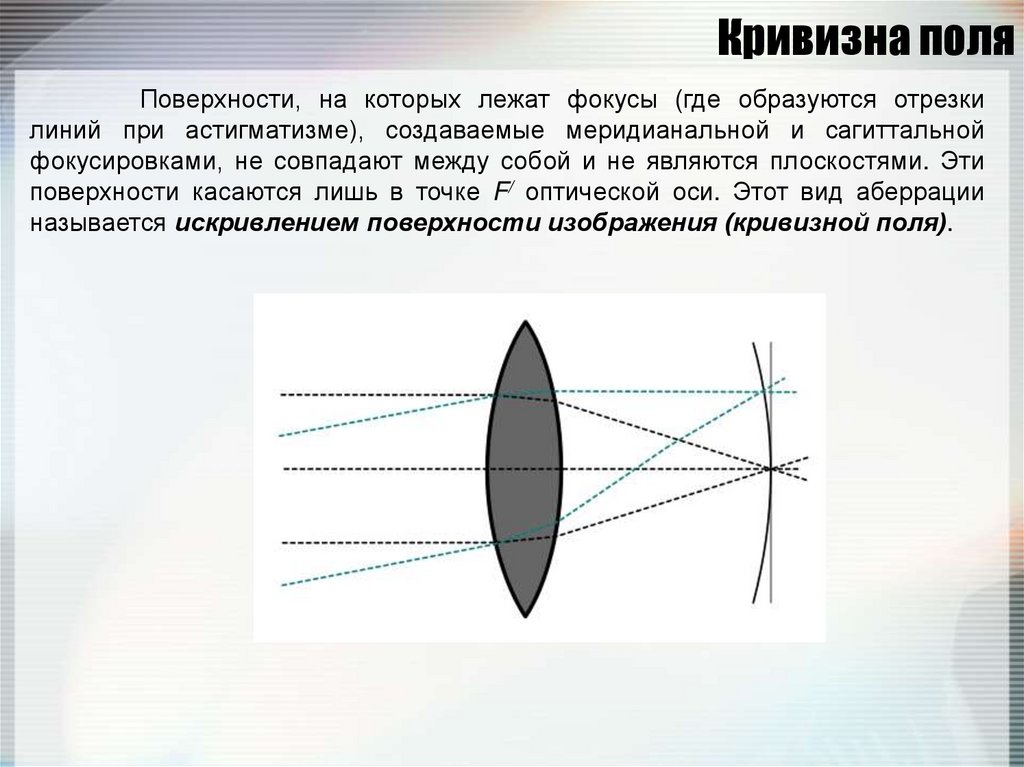

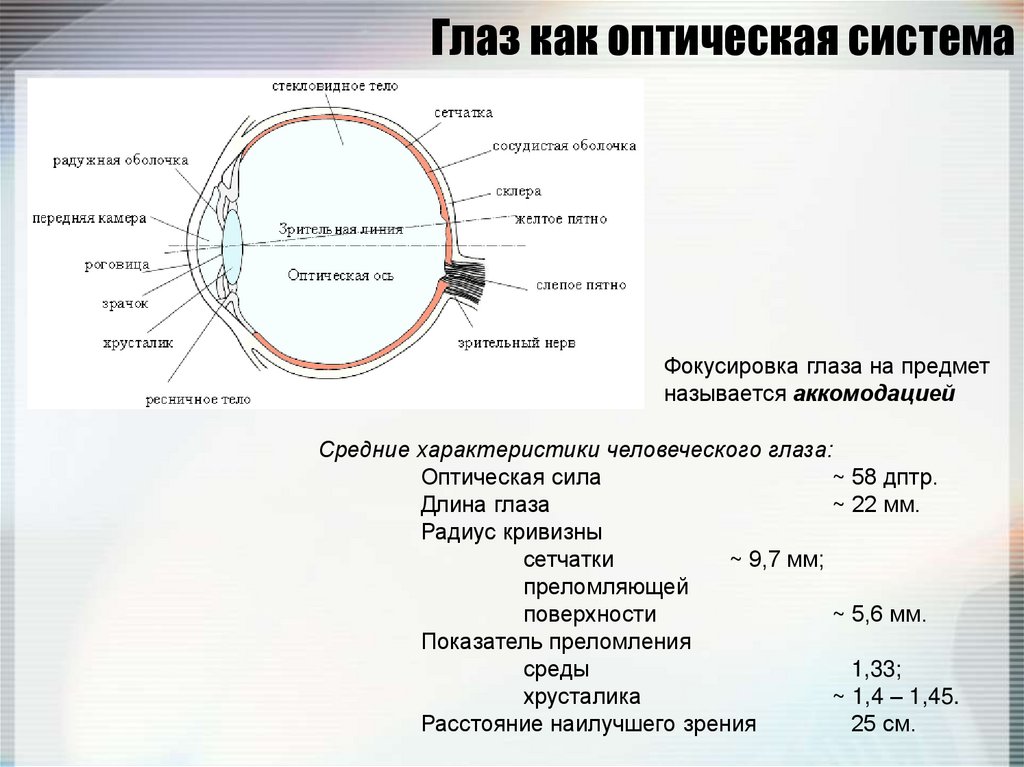

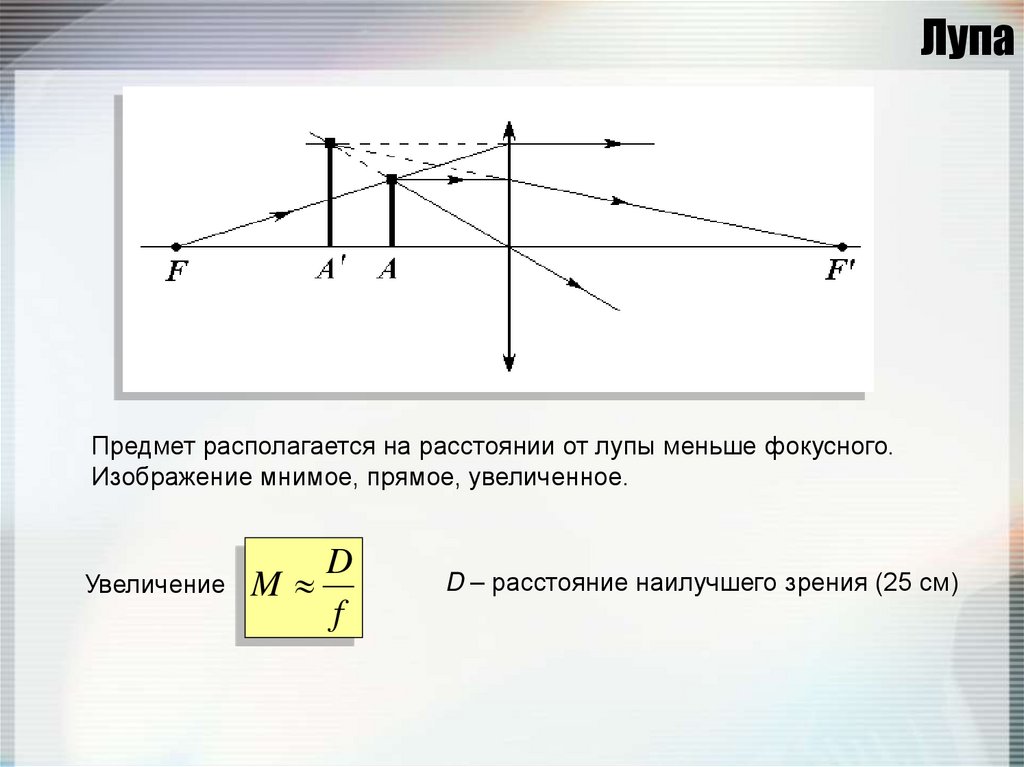
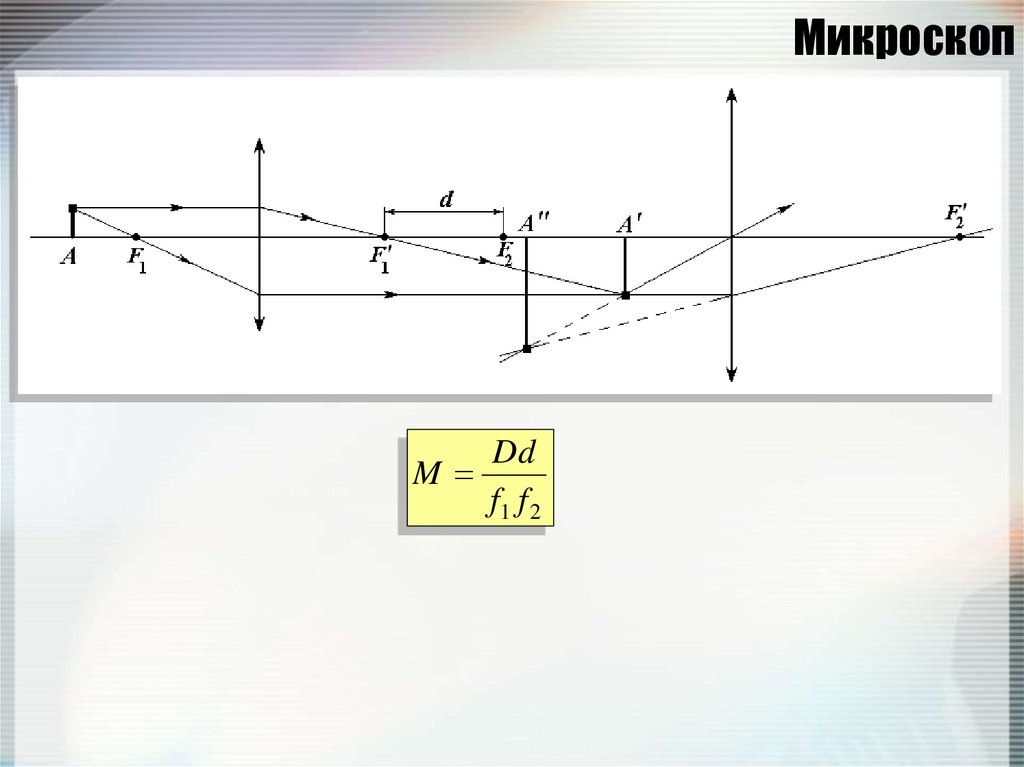






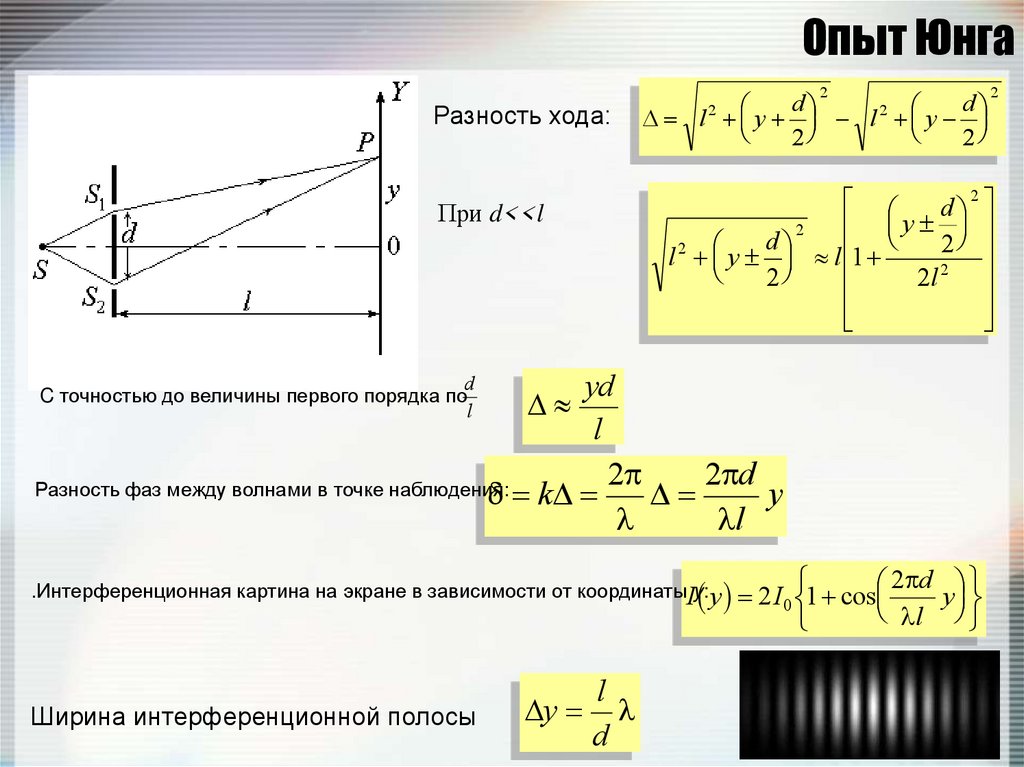
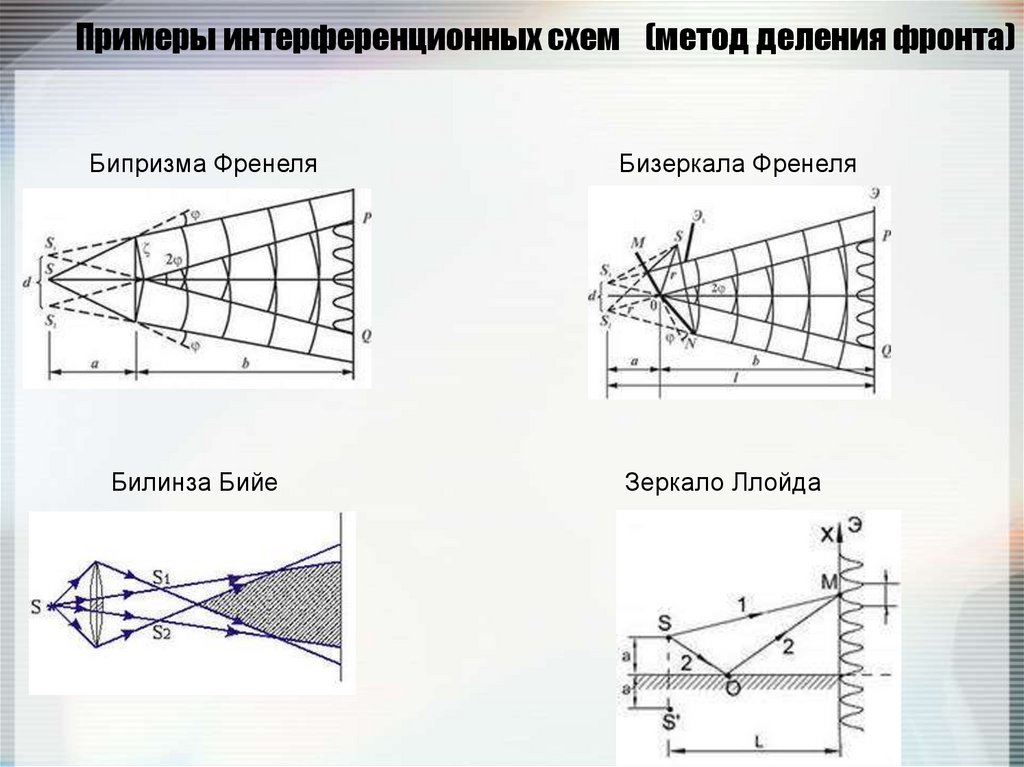


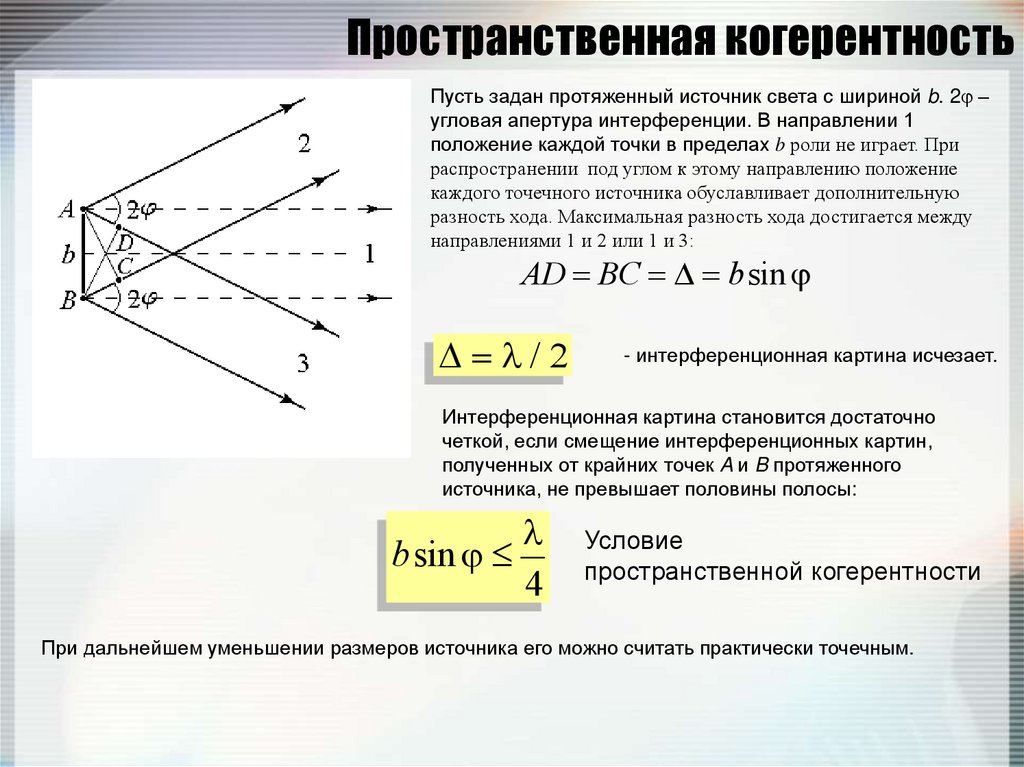


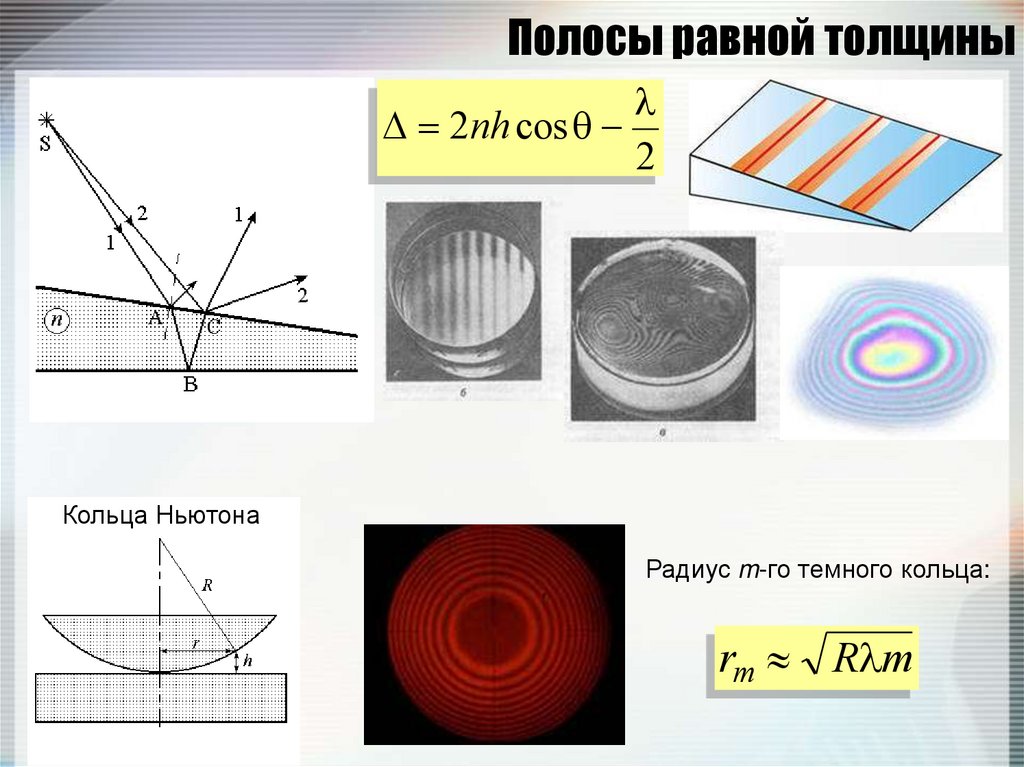

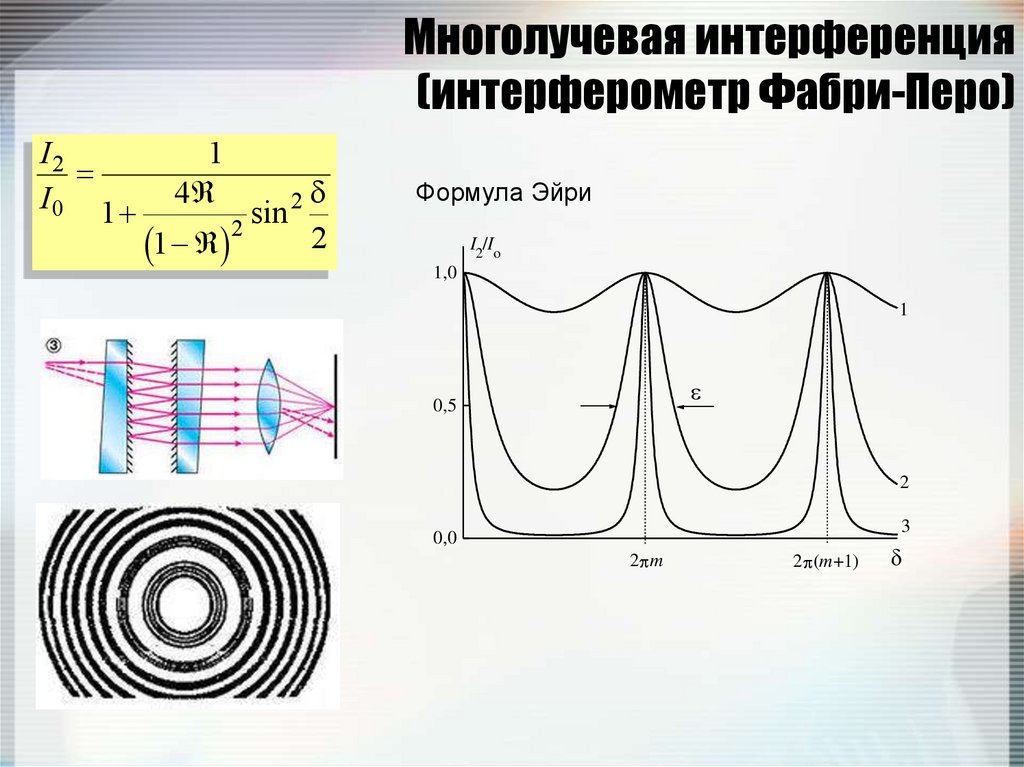


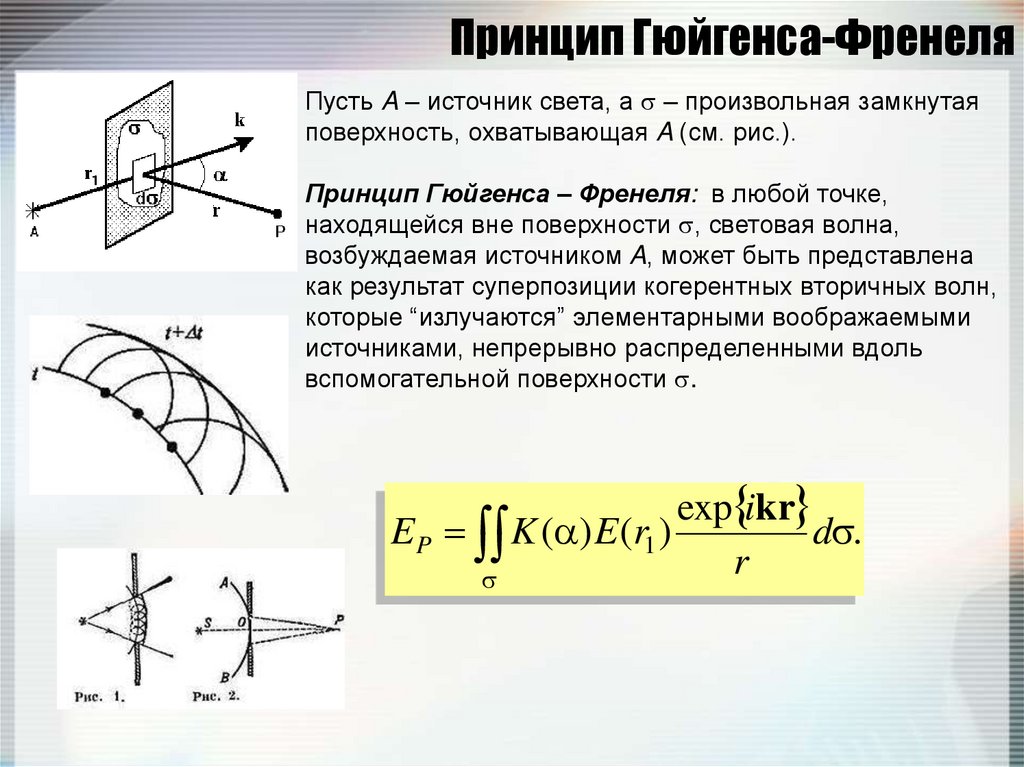


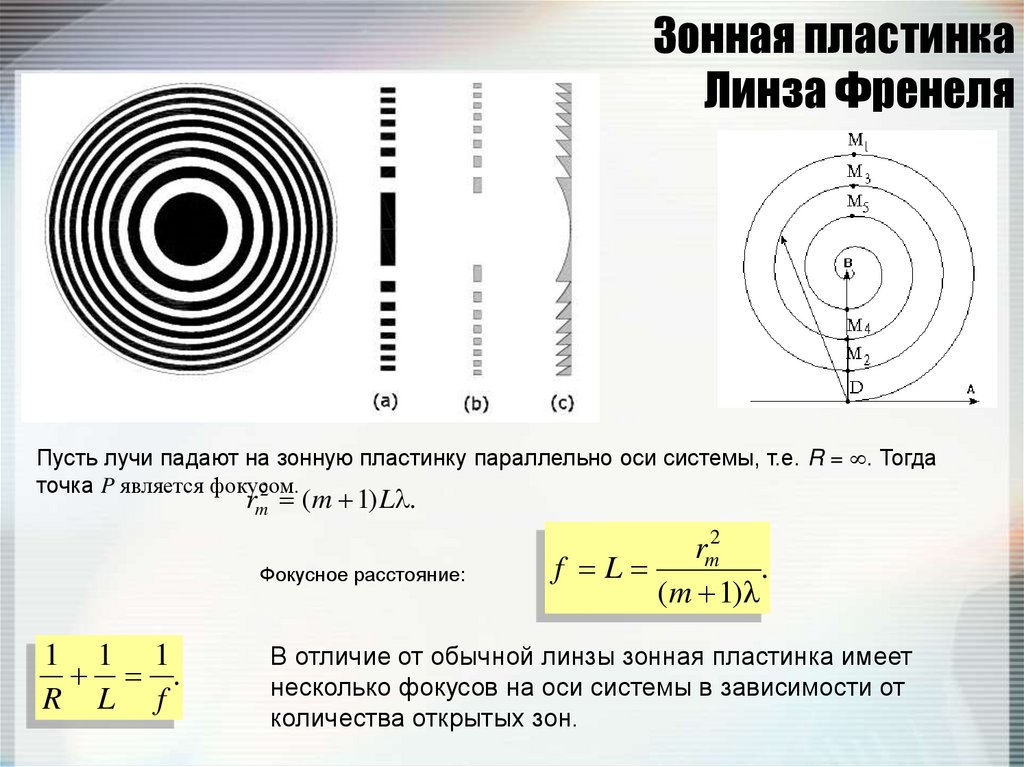

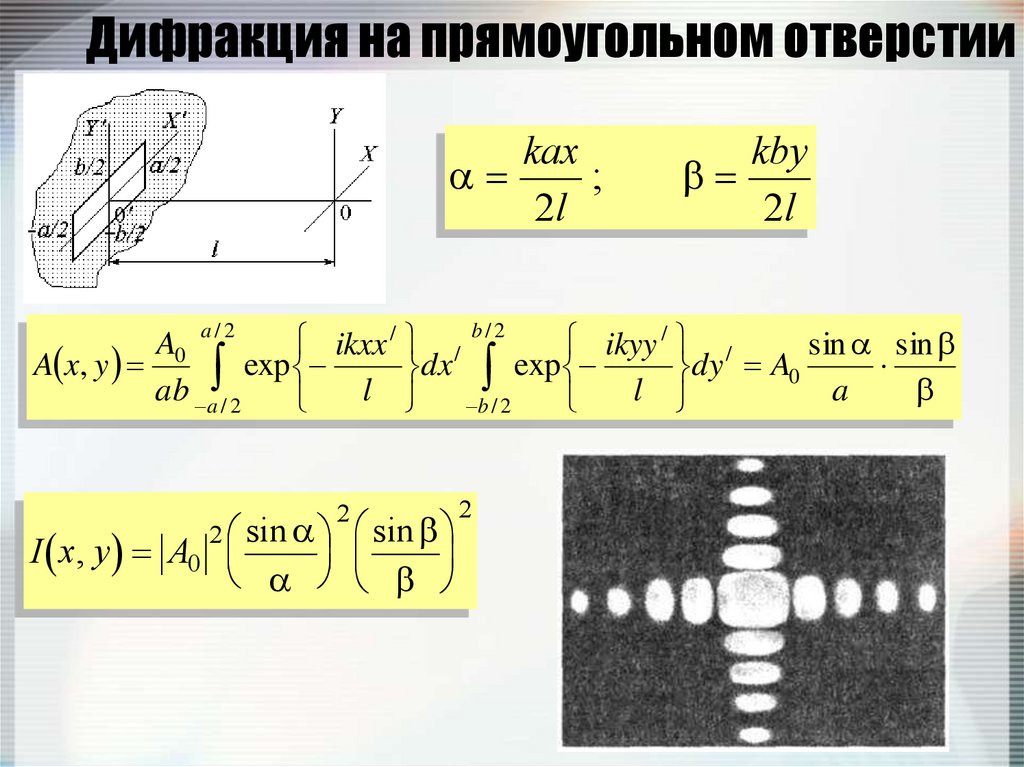
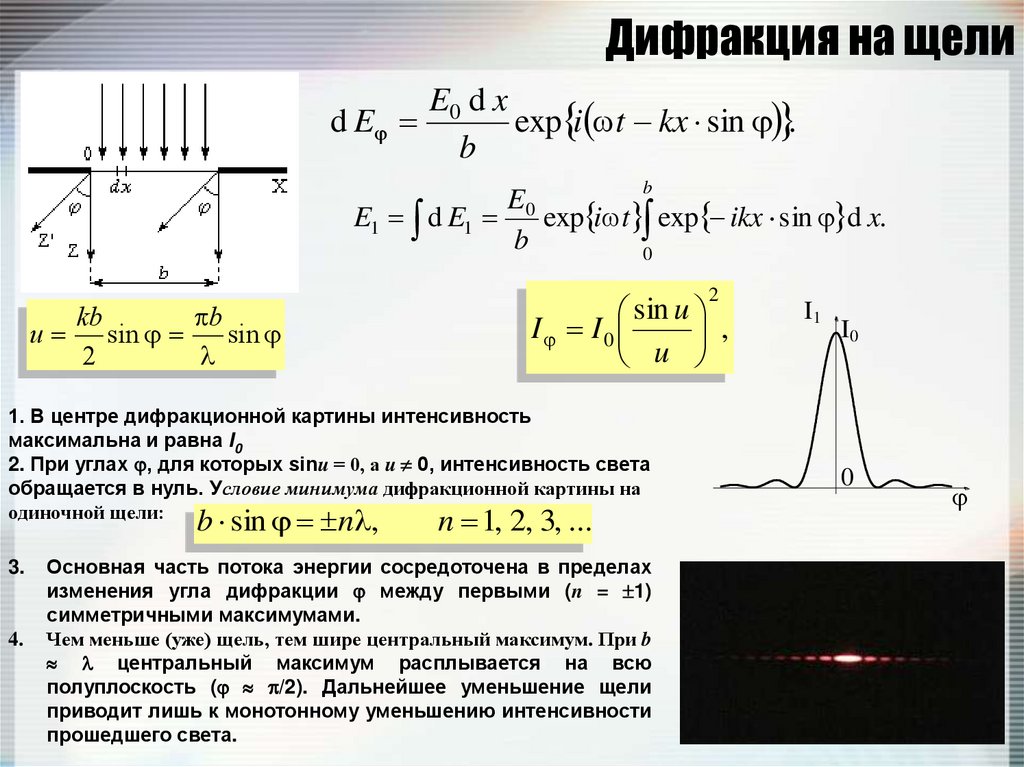
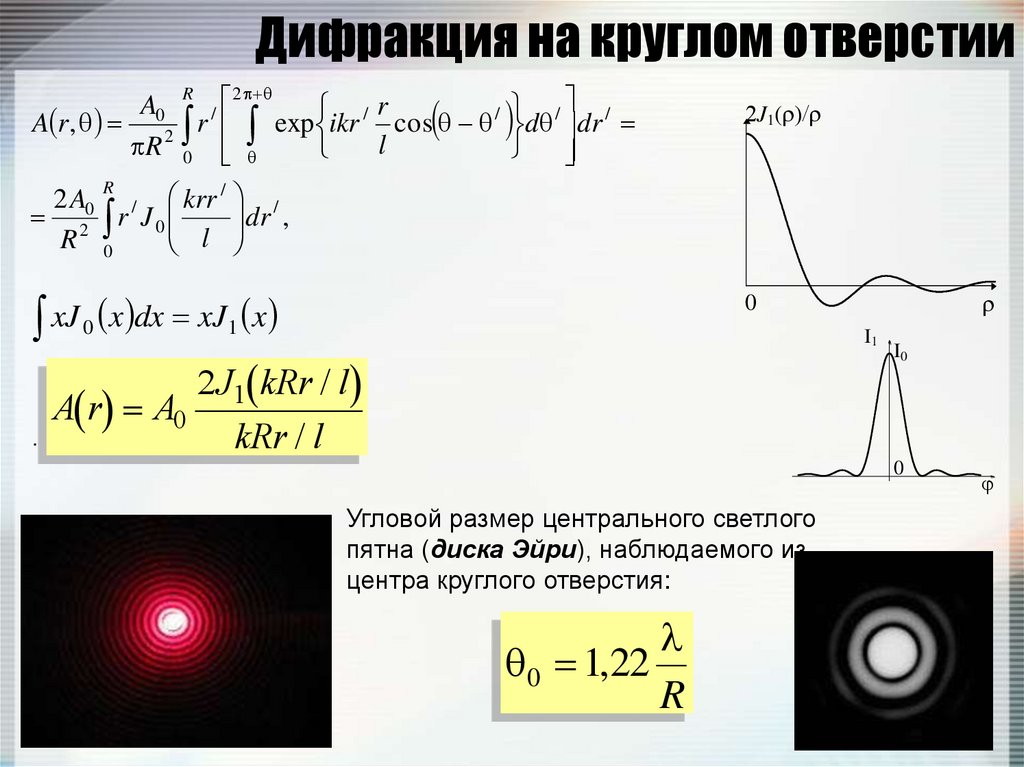
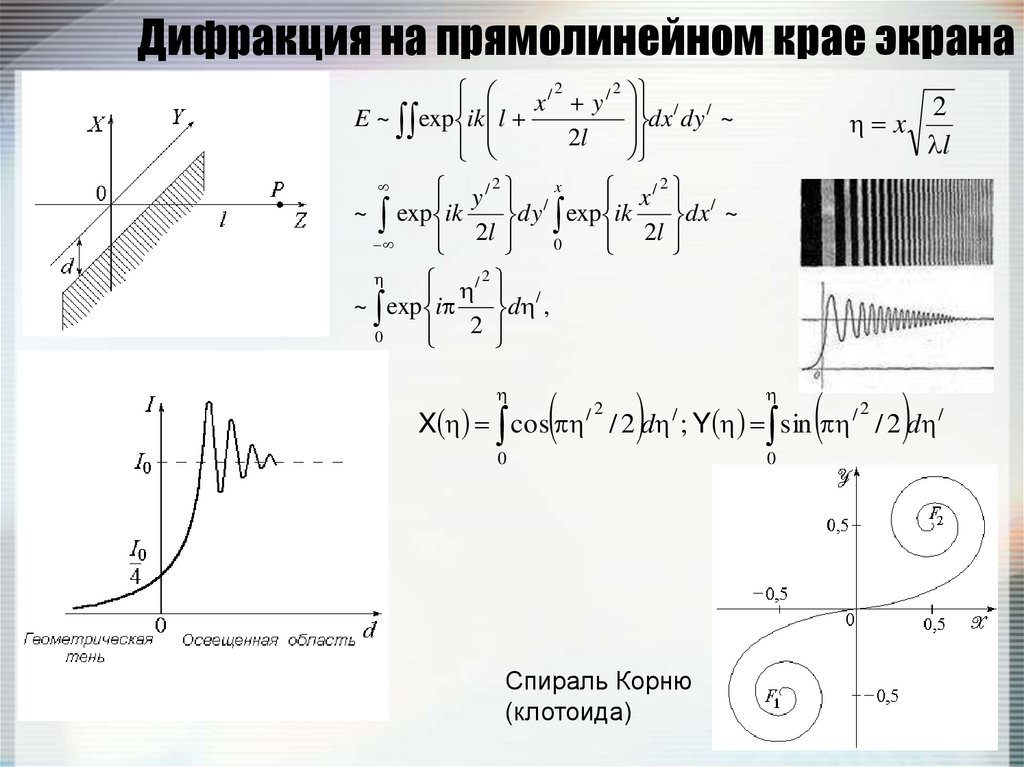




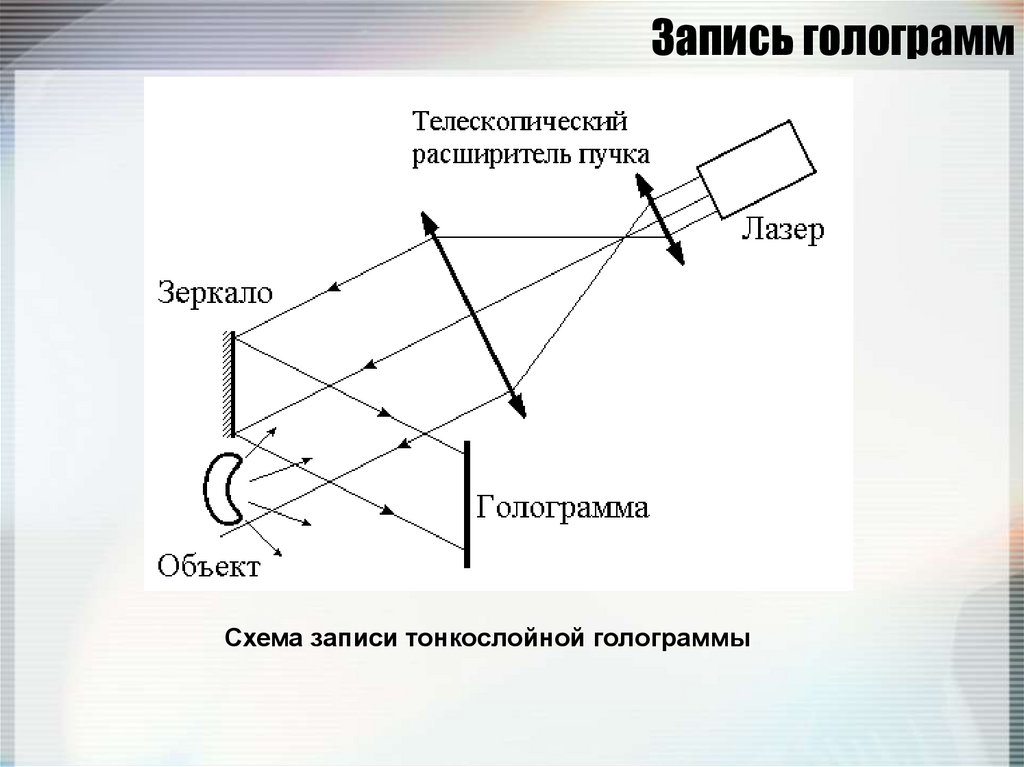

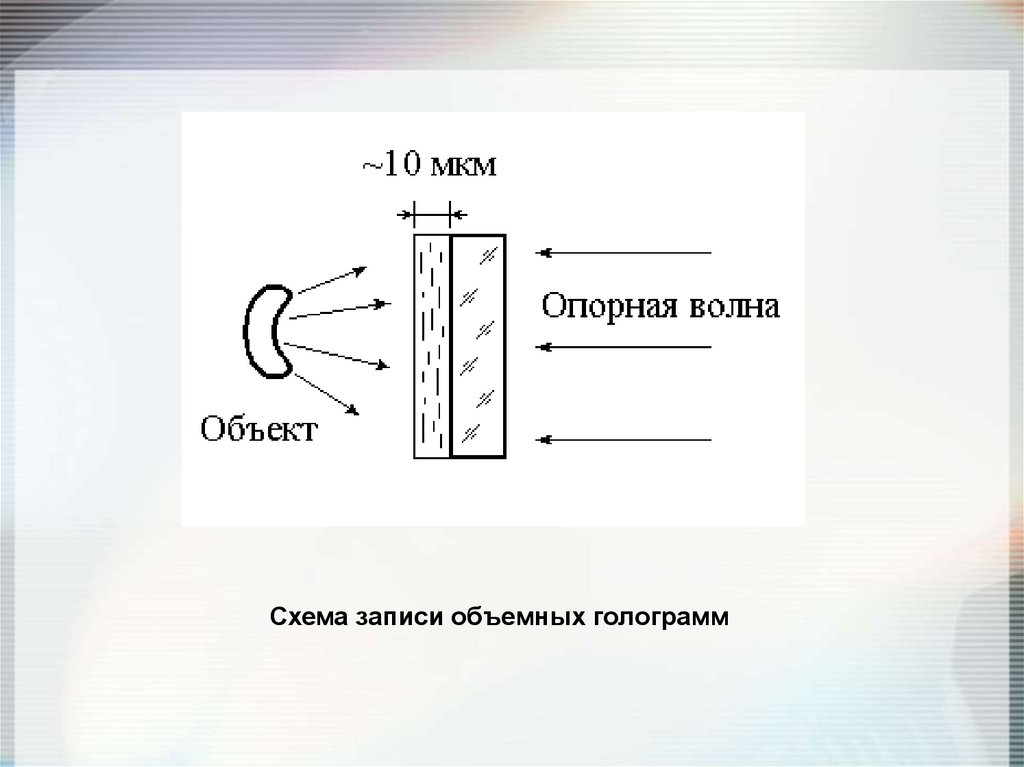




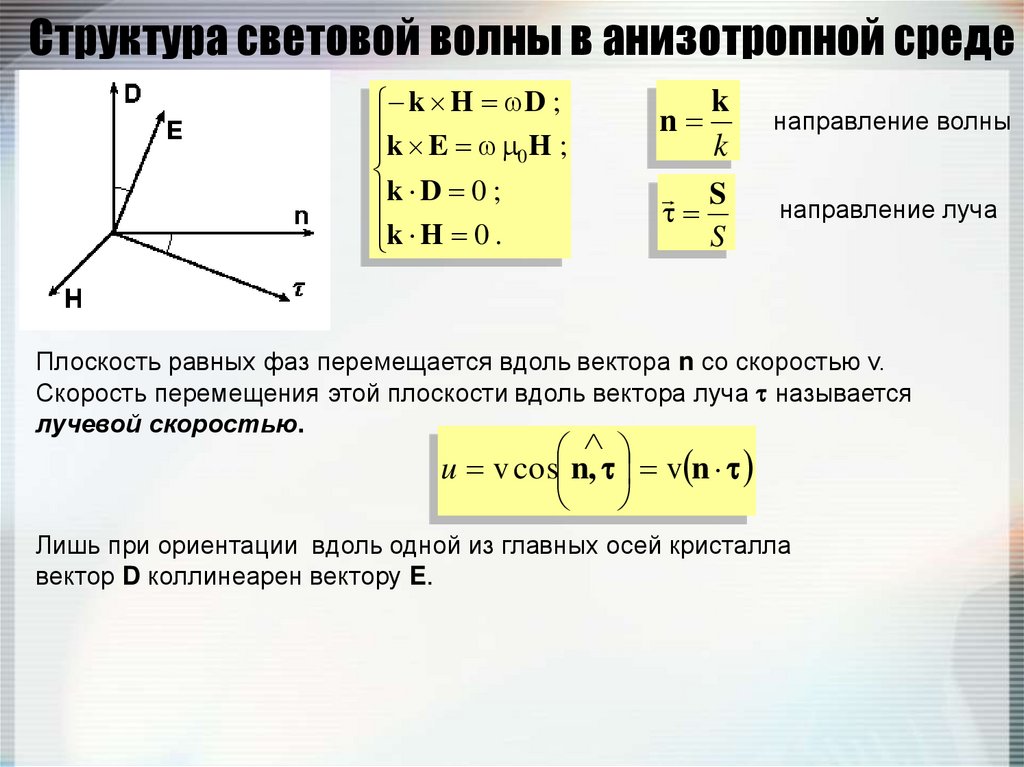

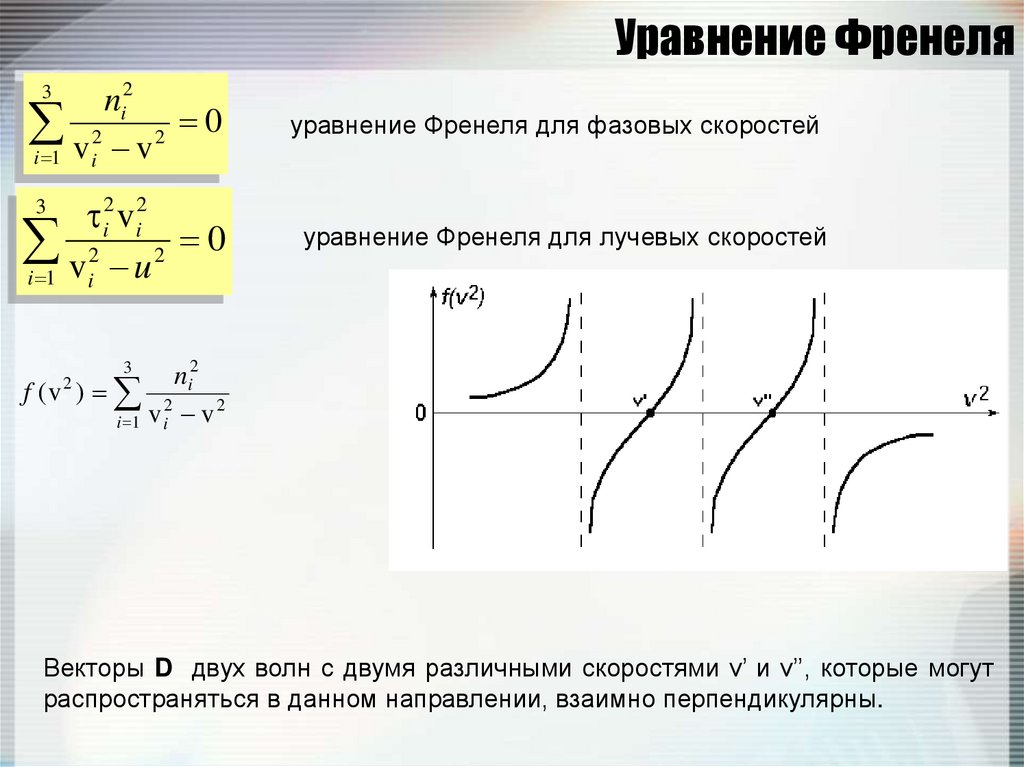






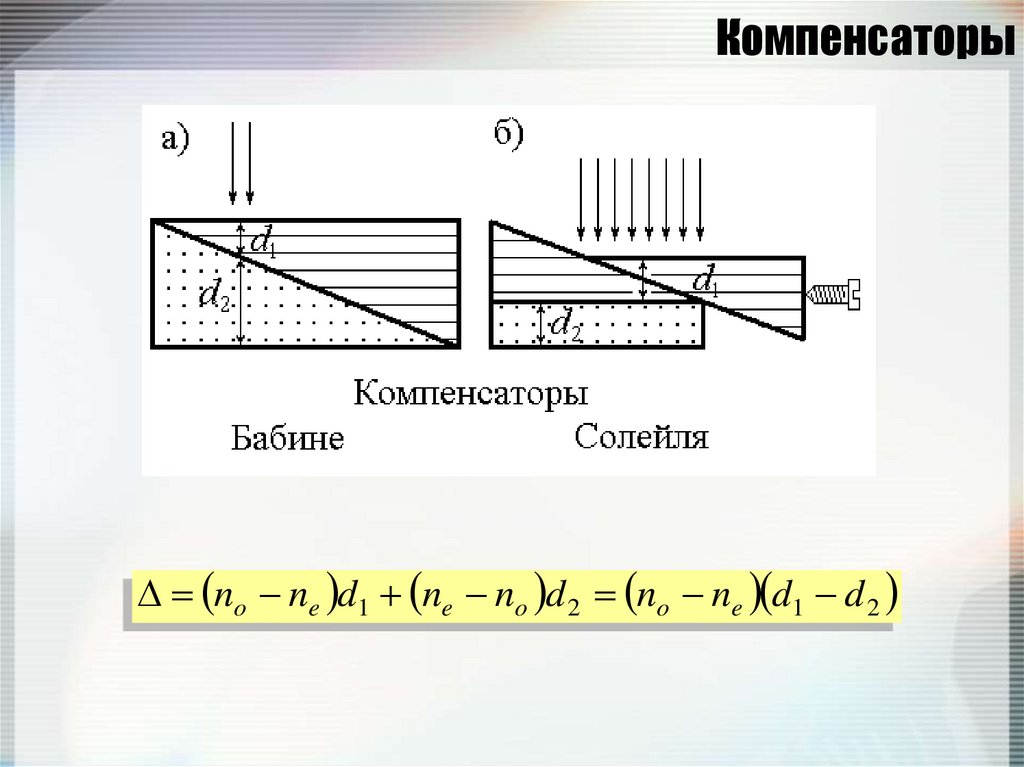

 Физика
Физика








