Балочные системы

1.

Балочные системы
Дудко Ольга Николаевна,
преподаватель Лидского колледжа ГрГУ им. Я.Купалы

2.

Перечень вопросов:
1. Нагрузки. Виды нагрузок, действующих
на балку.
2. Опоры. Виды опор. Реакции опор.
3. Методика решения задач на определение
реакций опор.

3.

4.

1.Нагрузки. Виды нагрузок,
действующих на балку

5.

Балочные системы
• Балка- это
элемент
конструкции,
размеры
поперечного
сечения которого
во много раз
меньше размеров
длины
• Балка ,несущая
нагрузку и
закреплённая на
опорах,
называется
балочной
системой

6.

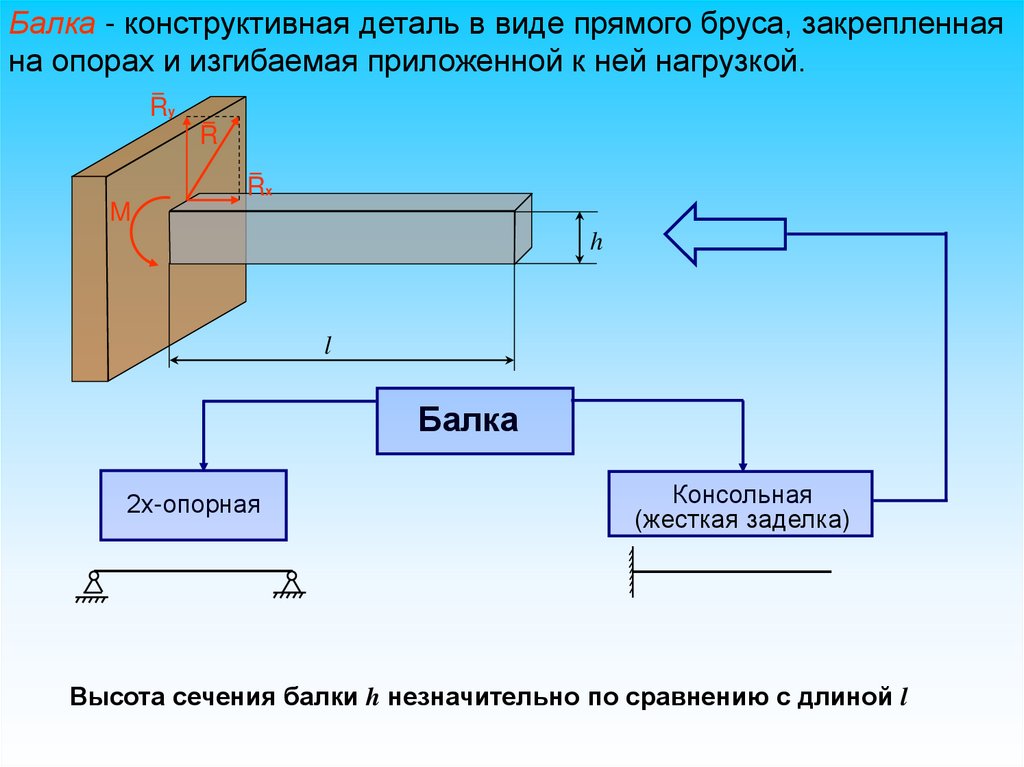
Балка - конструктивная деталь в виде прямого бруса, закрепленная
на опорах и изгибаемая приложенной к ней нагрузкой.
Ry
R
Rx
M
h
l
Балка
2х-опорная
Консольная
(жесткая заделка)
Высота сечения балки h незначительно по сравнению с длиной l

7.

В теоретической механике балки наряду
со стержнями являются центральным
объектом изучения.

8.

1. НАГРУЗКИ. ВИДЫ НАГРУЗОК.
На балку действуют следующие виды
нагрузок:
1.Сосредоточенная сила.
2.Распределенная нагрузка.
3.Пара сил.

9.

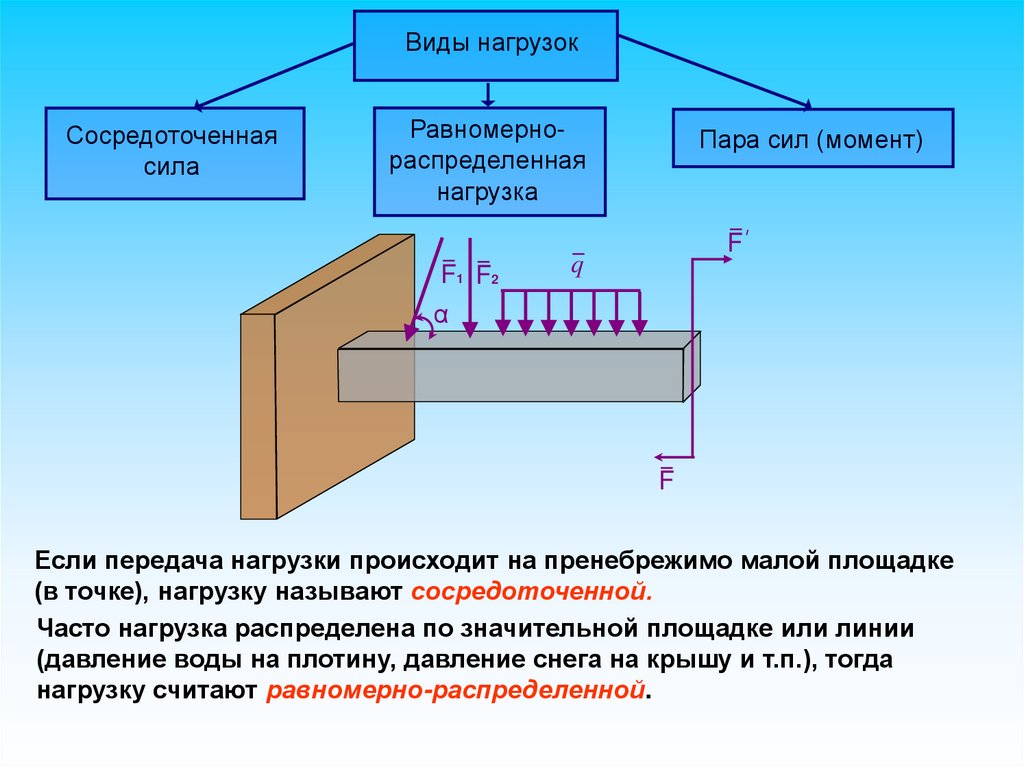
Виды нагрузок
Сосредоточенная
сила
Равномернораспределенная
нагрузка
F 1 F2
Пара сил (момент)
F
q
α
F
Если передача нагрузки происходит на пренебрежимо малой площадке
(в точке), нагрузку называют сосредоточенной.
Часто нагрузка распределена по значительной площадке или линии
(давление воды на плотину, давление снега на крышу и т.п.), тогда
нагрузку считают равномерно-распределенной.

10.

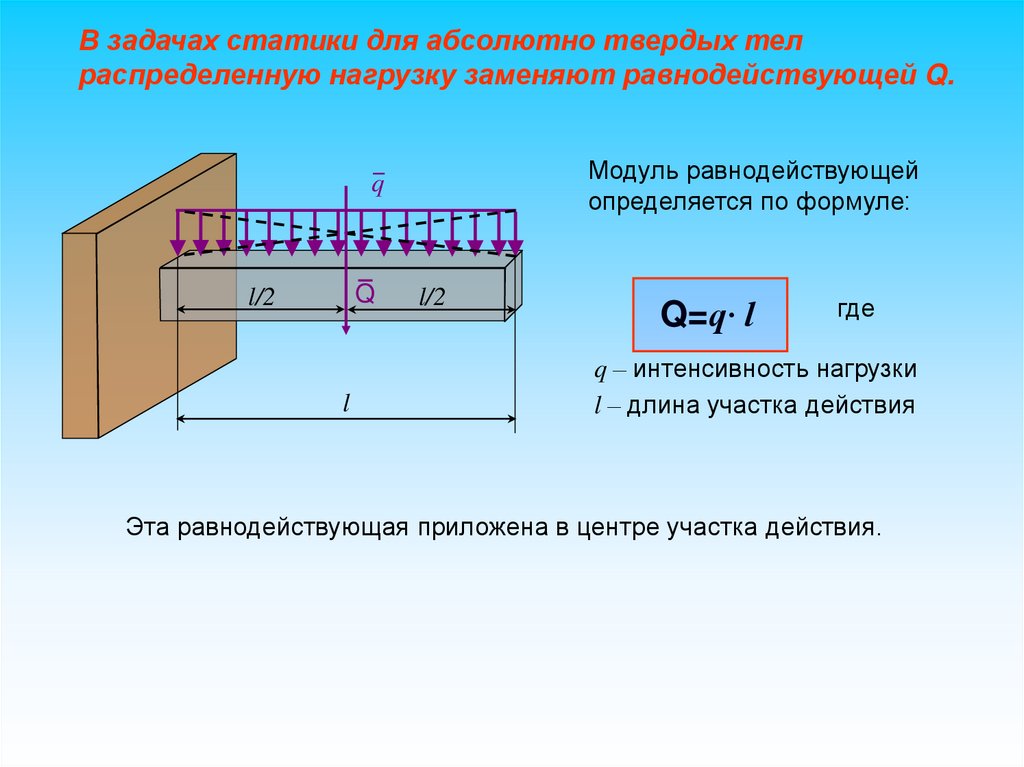
В задачах статики для абсолютно твердых тел
распределенную нагрузку заменяют равнодействующей Q.
Модуль равнодействующей
определяется по формуле:
q
Q
l/2
l
l/2
Q=q∙ l
где
q – интенсивность нагрузки
l – длина участка действия
Эта равнодействующая приложена в центре участка действия.

11.

Третьей нагрузкой может быть пара сил
с моментом М, изображенным в виде
дугообразной стрелки, указывающей
направление вращения пары сил.

12.

2.Опоры. Виды опор.
Реакции опор.

13.

2. ОПОРЫ.ВИДЫ ОПОР. РЕАКЦИИ ОПОР.
Между балкой и опорной
поверхностью находится опора –
устройство, предназначенное для
сопряжения балки с другими
элементами и передачи на них
усилий.

14.

15.

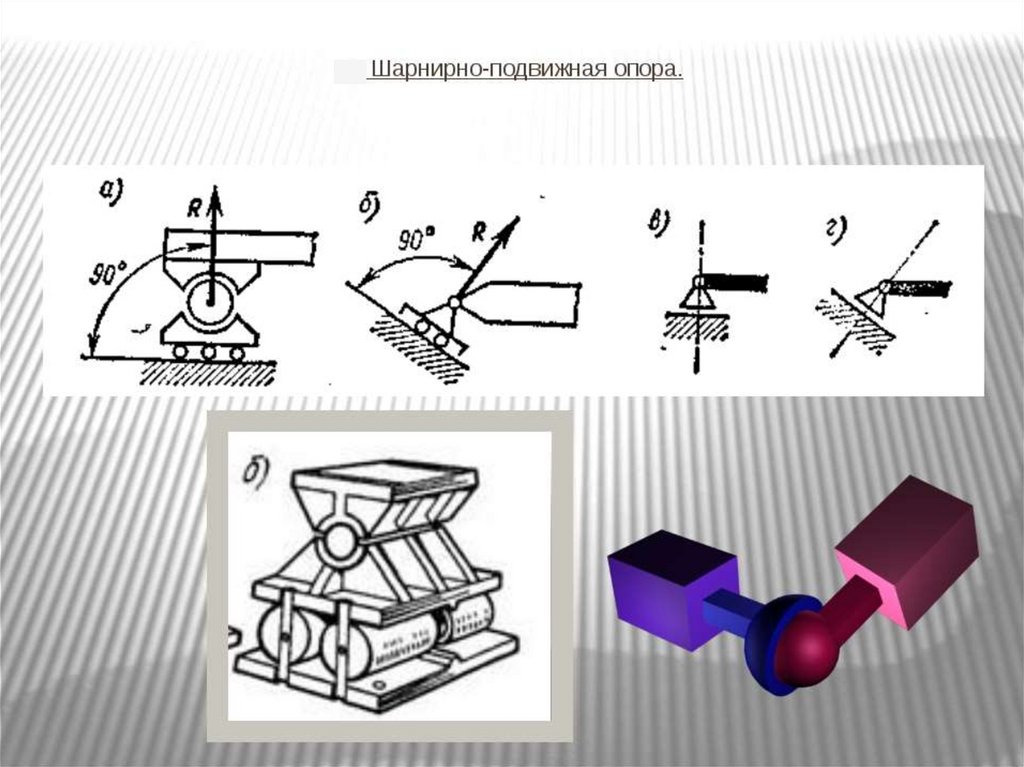
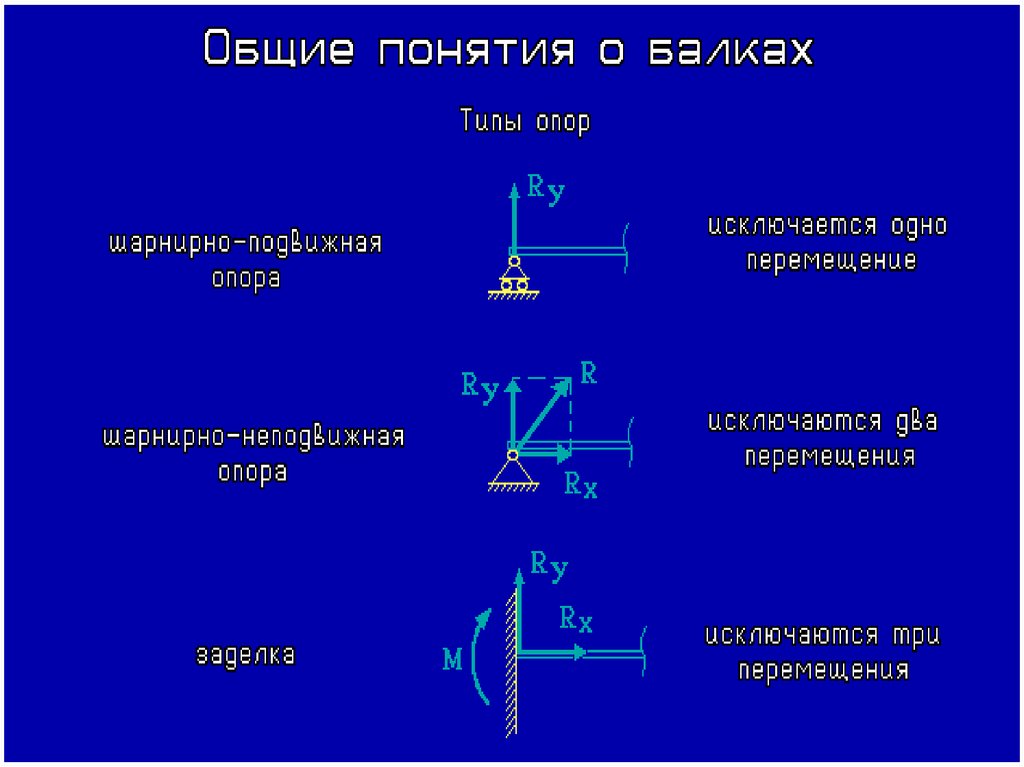
ВИДЫ ОПОР
1.Шарнирно- подвижная опора (ШПО).
Позволяет телу, находящемуся на
данной опоре поворачиваться на
небольшой угол относительно оси
шарнира и перемещаться на небольшие
расстояния относительно опорной
поверхности.

16.

ВИДЫ ОПОР

17.

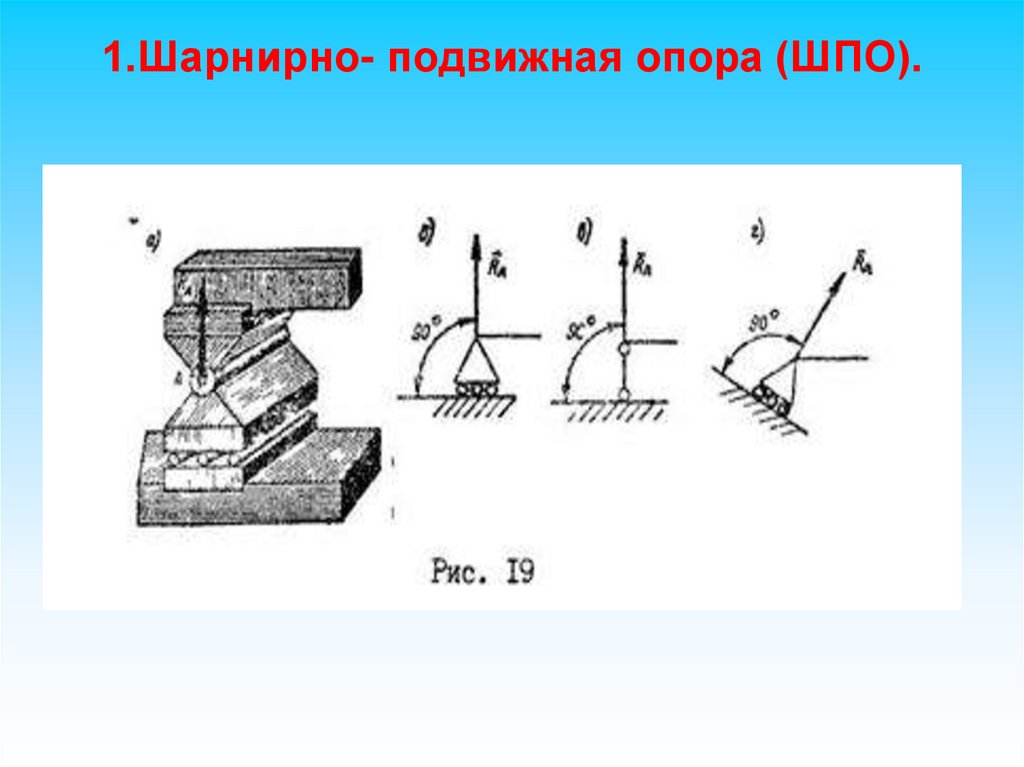
1.Шарнирно- подвижная опора (ШПО).

18.

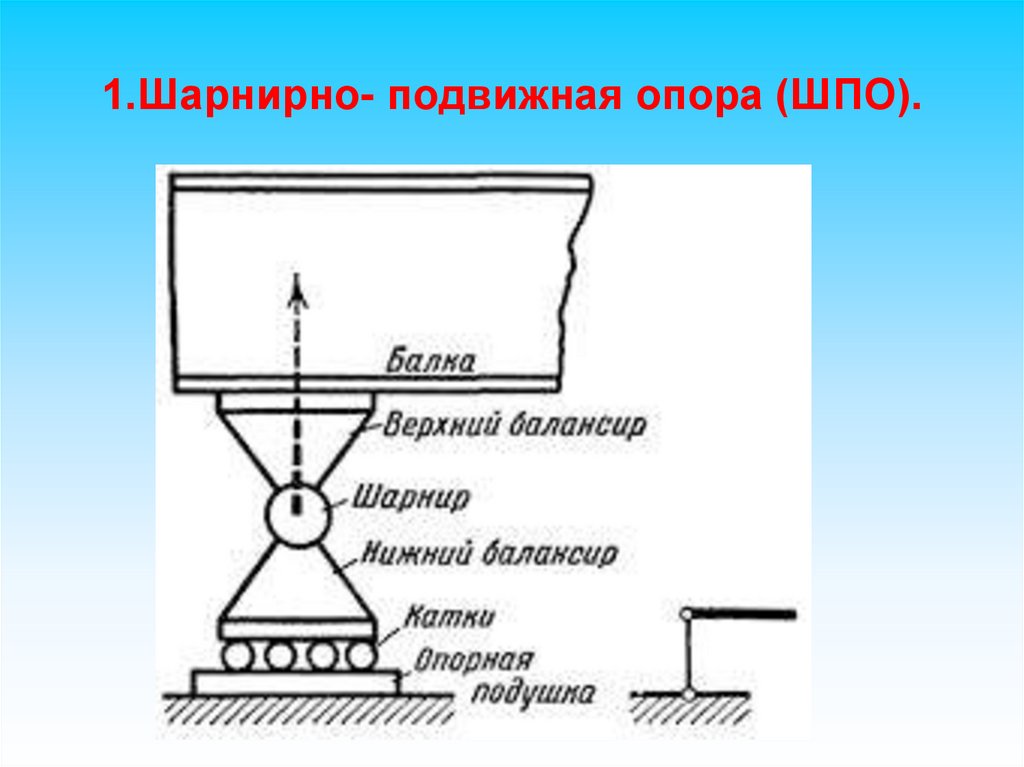
1.Шарнирно- подвижная опора (ШПО).

19.

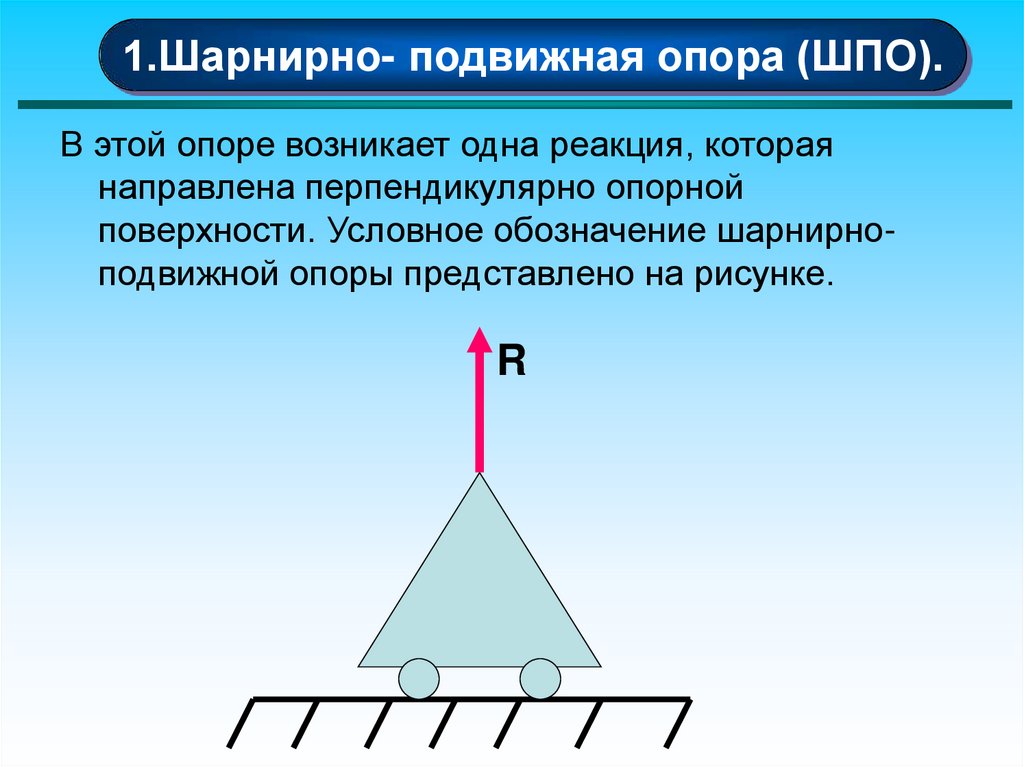
1.Шарнирно- подвижная опора (ШПО).
В этой опоре возникает одна реакция, которая
направлена перпендикулярно опорной
поверхности. Условное обозначение шарнирноподвижной опоры представлено на рисунке.
R

20.

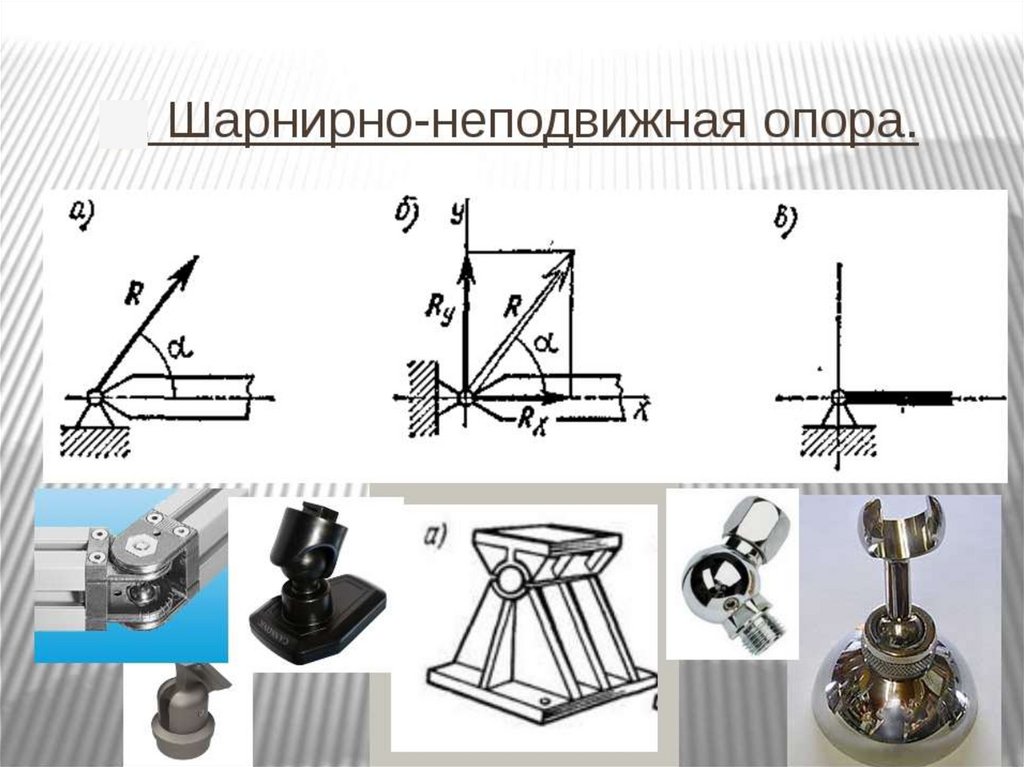
ВИДЫ ОПОР
2.Шарнирно- неподвижная опора (ШПО).
Позволяет телу, находящемуся на данной
опоре поворачиваться на небольшой угол
относительно оси шарнира. Линейных
перемещений не допускает.

21.

22.

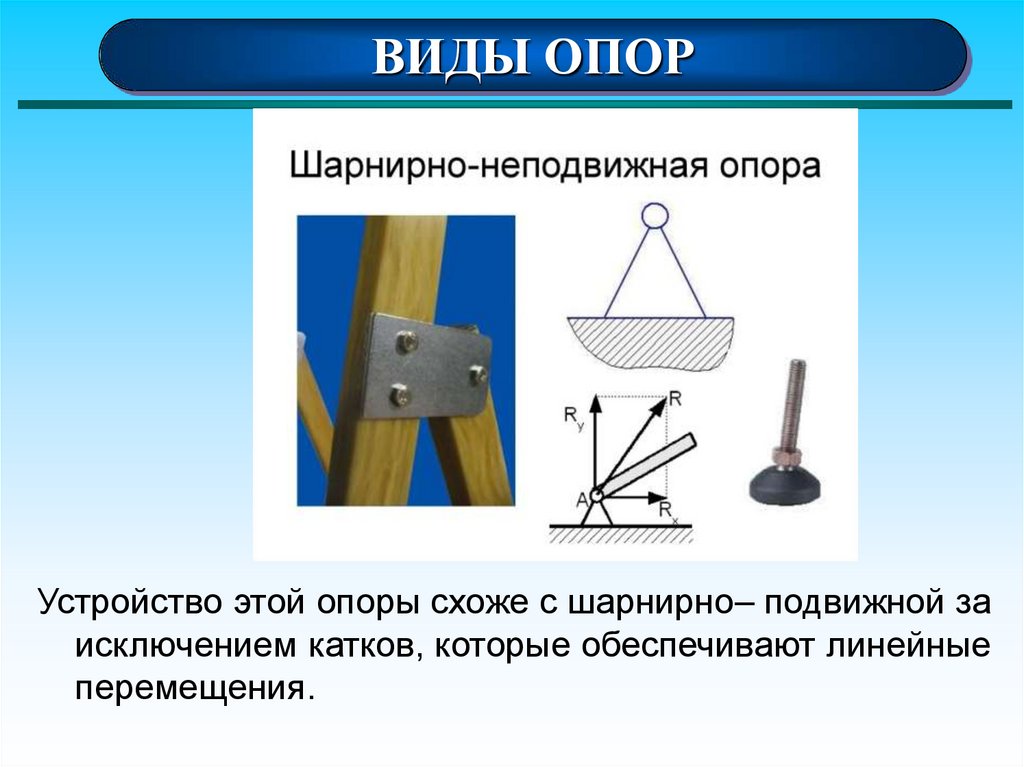
ВИДЫ ОПОР
Устройство этой опоры схоже с шарнирно– подвижной за
исключением катков, которые обеспечивают линейные
перемещения.

23.

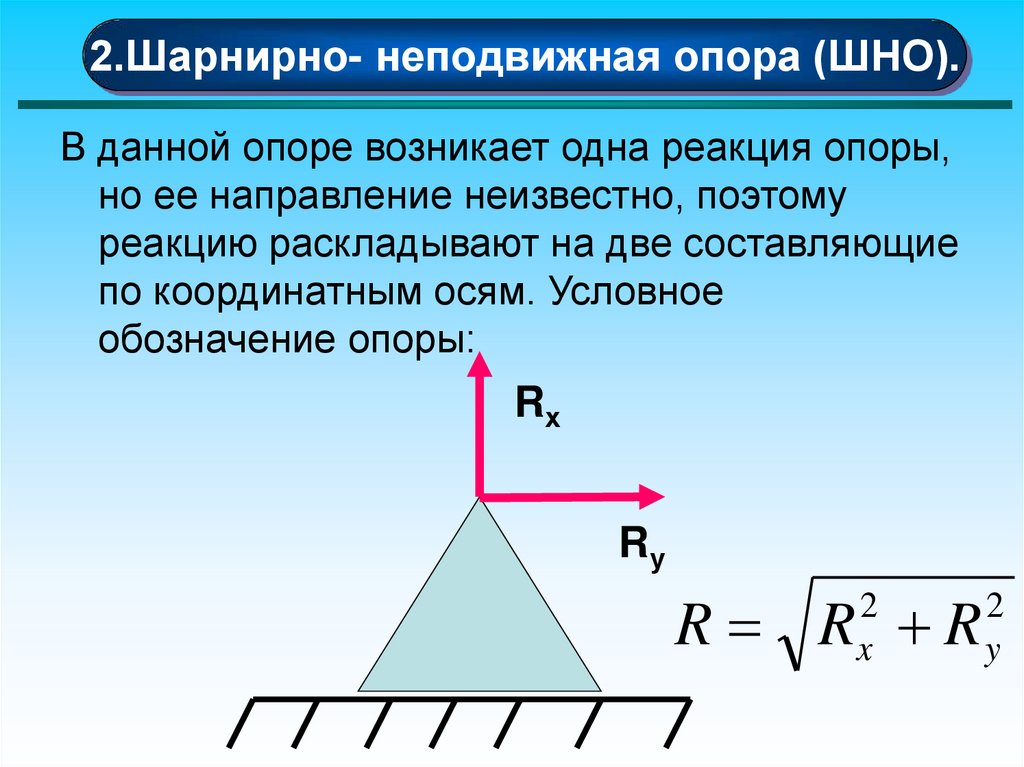
2.Шарнирно- неподвижная опора (ШНО).
В данной опоре возникает одна реакция опоры,
но ее направление неизвестно, поэтому
реакцию раскладывают на две составляющие
по координатным осям. Условное
обозначение опоры:
Rх
Rу
R R R
2
x
2
y

24.

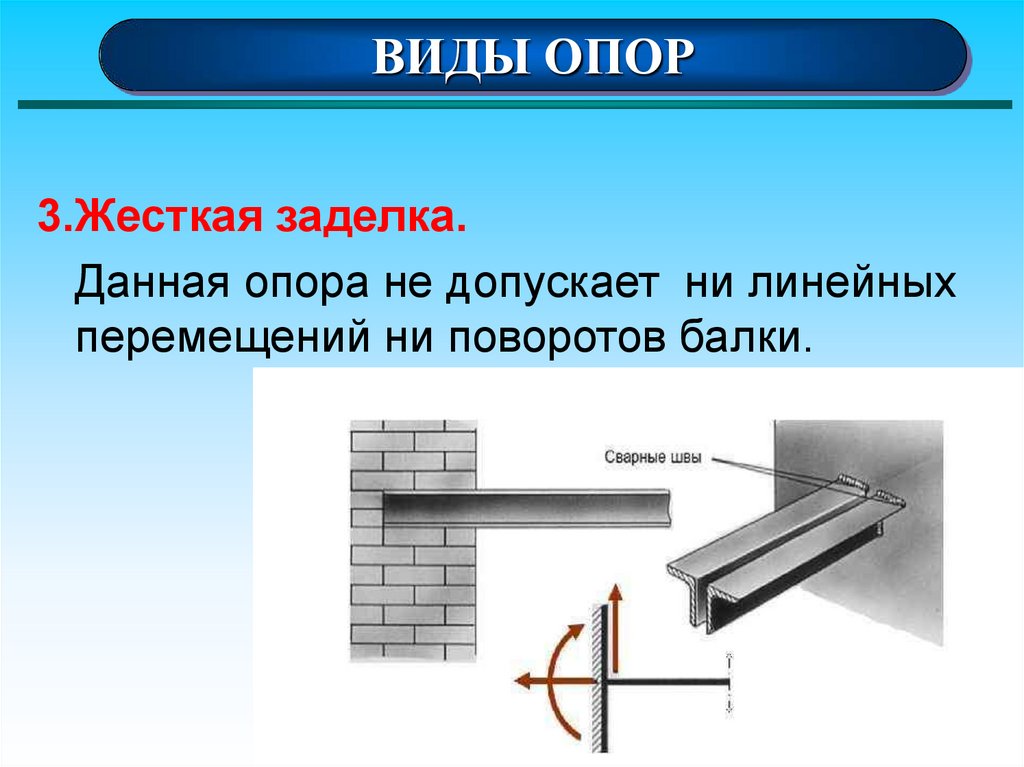
ВИДЫ ОПОР
3.Жесткая заделка.
Данная опора не допускает ни линейных
перемещений ни поворотов балки.

25.

26.

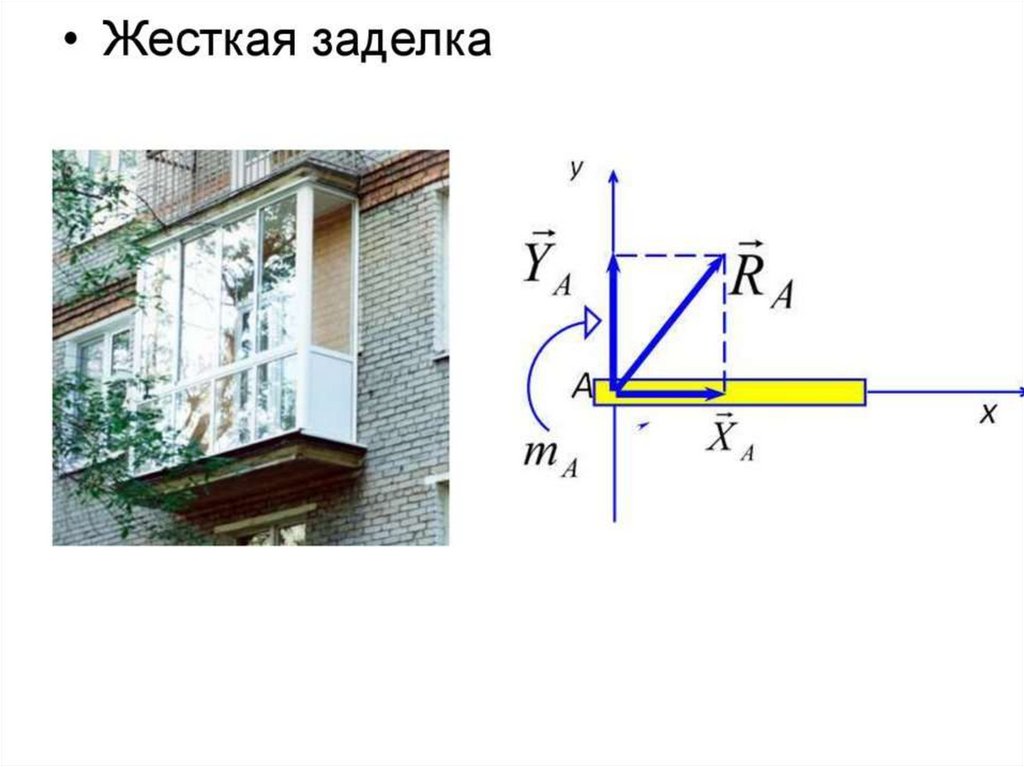
3.Жесткая заделка.
В этой опоре возникают две реакции:
• -пара сил с моментом М
• -реакция R, направление которой
неизвестно, поэтому ее раскладывают на две
составляющие по координатным осям
R R R
2
x
2
y

27.

28.

Примеры опор на практике
• Самым распространенным примером
является мост (ж\д мост )

29.

Шарнирноподвижная опора
моста

30.

Шарнирно неподвижная опора
моста

31.

32.

Примеры опор в автомобиле
Коленчатый вал с подшипниками

33.

Примеры опор в автомобиле
Валы редуктора на
подшипниках качения

34.

3. Методика решения задач на
определение реакций опор.

35.

Шаг 1.
На расчетной схеме расставляем центры
моментов (в качестве центров
моментов А и В рекомендуется
выбирать точку, где пересекаются
неизвестные силы).

36.

Шаг 2.
Заменяем опоры реакциями опор.
Шаг 3.
Выбираем
координатные
оси.
Оси
следует выбирать так, чтобы они были
перпендикулярны
некоторым
неизвестным силам.

37.

Шаг 4.
Составляем уравнения равновесия для
полученной системы произвольнорасположенных сил, общий вид
которых:
• ΣМА(F) = 0
• ΣМВ(F) = 0
• ΣFix = 0

38.

Шаг 5.
Решаем полученную систему
уравнений, из которой находим
неизвестные реакции опор.
Шаг 6.
Проверяем правильность решения при
помощи уравнения :
ΣFiу = 0

39.

Шаг 7.
Для нахождения полного значения
реакции в шарнирно- неподвижной
опоре или жесткой заделке
воспользуемся формулой :
R R R
2
x
2
y

40.

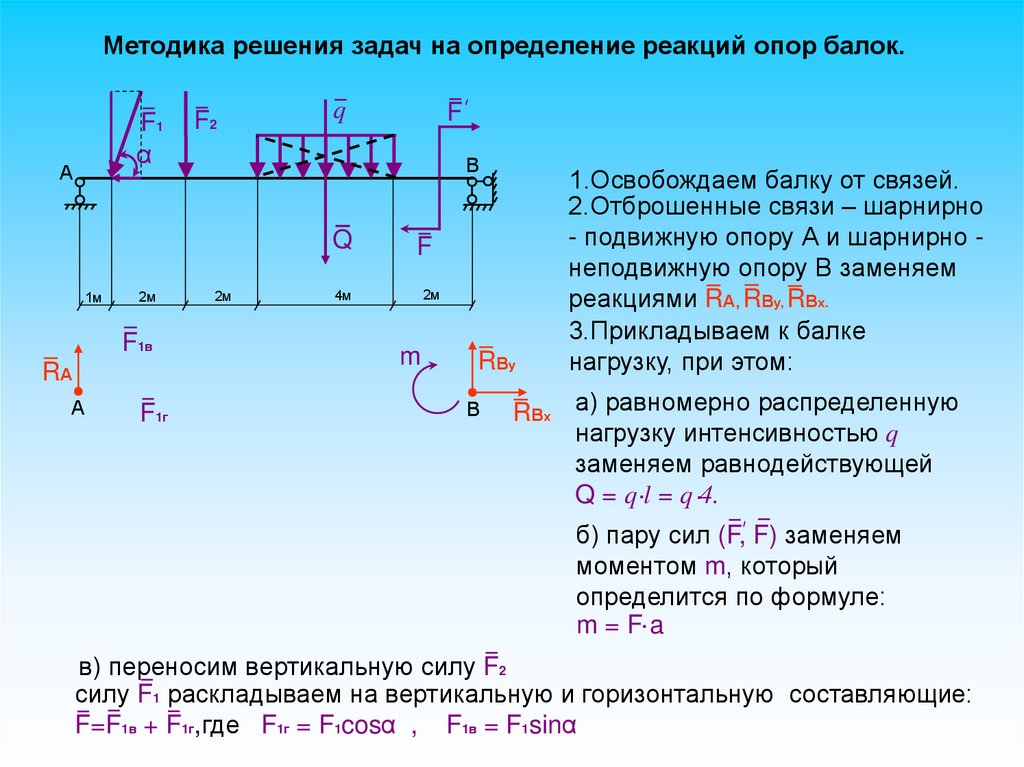
Методика решения задач на определение реакций опор балок.
F1
α
А
F2
q
В
Q
1м
2м
F1в
RА
А
F1г
F
2м
F
2м
4м
m
RВу
В
1.Освобождаем балку от связей.
2.Отброшенные связи – шарнирно
- подвижную опору А и шарнирно неподвижную опору В заменяем
реакциями RА, RВу, RВх.
3.Прикладываем к балке
нагрузку, при этом:
RВх а) равномерно распределенную
нагрузку интенсивностью q
заменяем равнодействующей
Q = q .l = q .4.
б) пару сил (F, F) заменяем
моментом m, который
определится по формуле:
m = F. a
в) переносим вертикальную силу F2
силу F1 раскладываем на вертикальную и горизонтальную составляющие:
F=F1в + F1г,где F1г = F1cosα , F1в = F1sinα

41.

у
F1в
F2
m
RА
А
В
F1г
1м
3м
Q
7м
1м
2м
1м
2м
RВу
11м10м 8 м
4м
2м
∑Fkx=0
∑mА(Fk)=0
4м
4м
4м
2м
RВх
4) Определяем расстояние
между линиями действия сил.
х 5) К полученной системе сил
применяем условия
равновесия в форме (А),
предварительно выбрав оси
координат.
Составляем 3 ур – я равновесия:
; - F1г + RBx = 0
; -RBy .11 +m +Q .7 + F2. 3+ F1B. 1 = 0
. - F2 .8 - Q .4 + m = 0
. - F1B 10
; RA 11
∑mВ(Fk)=0
Из каждого уравнения выражаем свои неизвестные:
RBx = F1г
из (1)
m + Q .7 + F2 .3 + F1B .1
из (2)
RBy =
11
F1B .10 + F2. 8 + Q.4 – m
из (3)
RA =
11
(1)
(2)
(3)
6) Осуществляем проверку правильности решения, составляя уравнение
равновесия ∑Fkу=0 ; RA – F1B – F2 – Q + RB = 0

42.

Примечание:
1. Выбирая одну из трех форм условия равновесия, запомнить правило :
а) если балка консольная (т.е. имеет одну связь), то применять основную
форму - ту, где используется одно уравнение моментов:
В
А
∑Fkх=0
∑Fkу=0
∑mА(Fk)=0
б) если балка 2х – опорная (т.е. имеет две связи), то применять форму (А) ту, где используются два уравнения моментов:
А
∑Fkx=0
В
∑mА(Fk)=0
∑mВ(Fk)=0
2. В качестве проверочного выбирают возможное неиспользованное уравнение
из другой формы:
а) для консольной балки
б) для 2х – опорной балки ∑Fkу=0

43.

Закрепление
пройденного
материала

44.

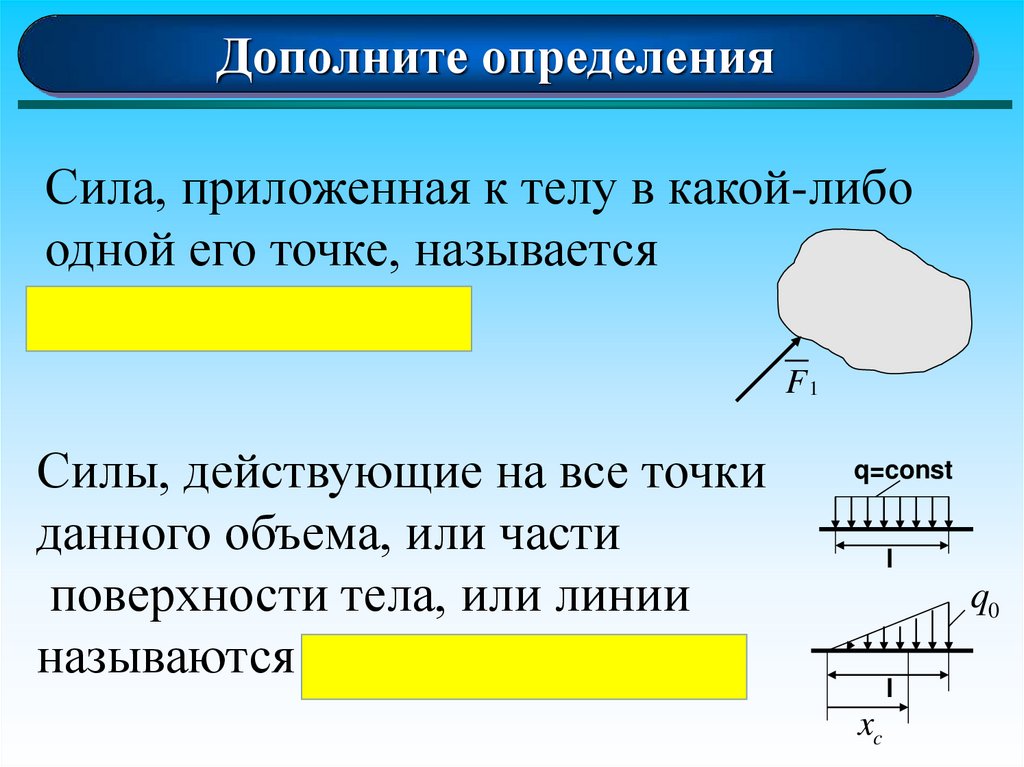
Дополните определения
Сила, приложенная к телу в какой-либо
одной его точке, называется
сосредоточенной.
F1
Силы, действующие на все точки
данного объема, или части
поверхности тела, или линии
называются распределенными.
q=const
l
q0
l
xc

45.

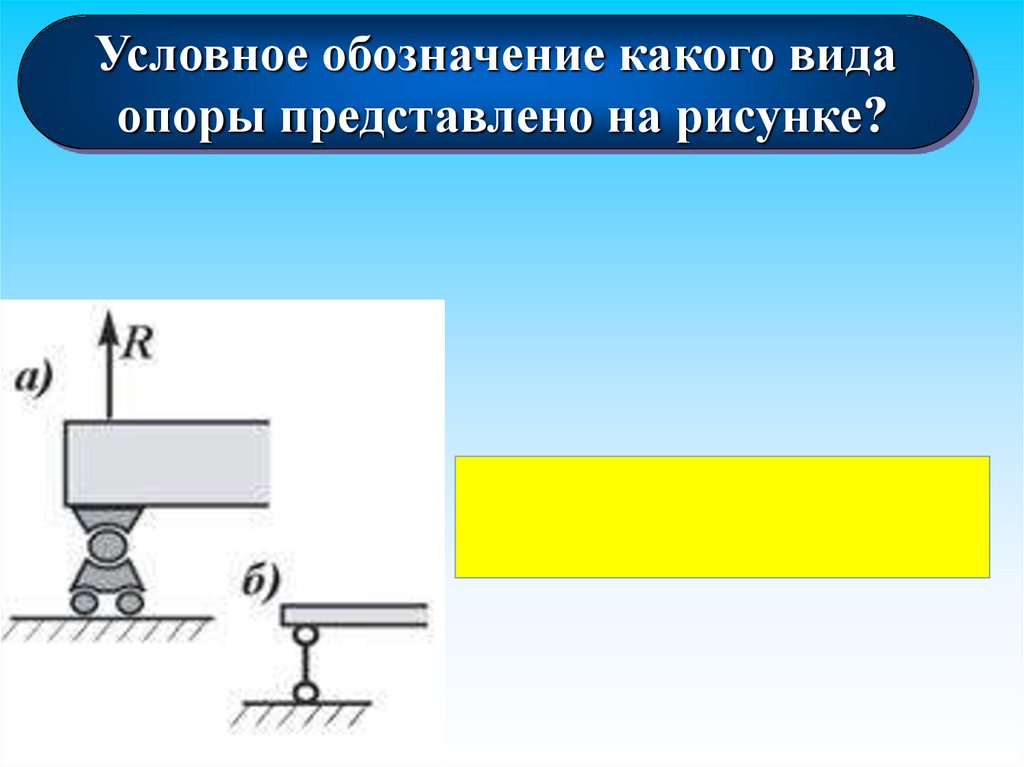
Условное обозначение какого вида
опоры представлено на рисунке?
шарнирно- подвижной
опоры

46.

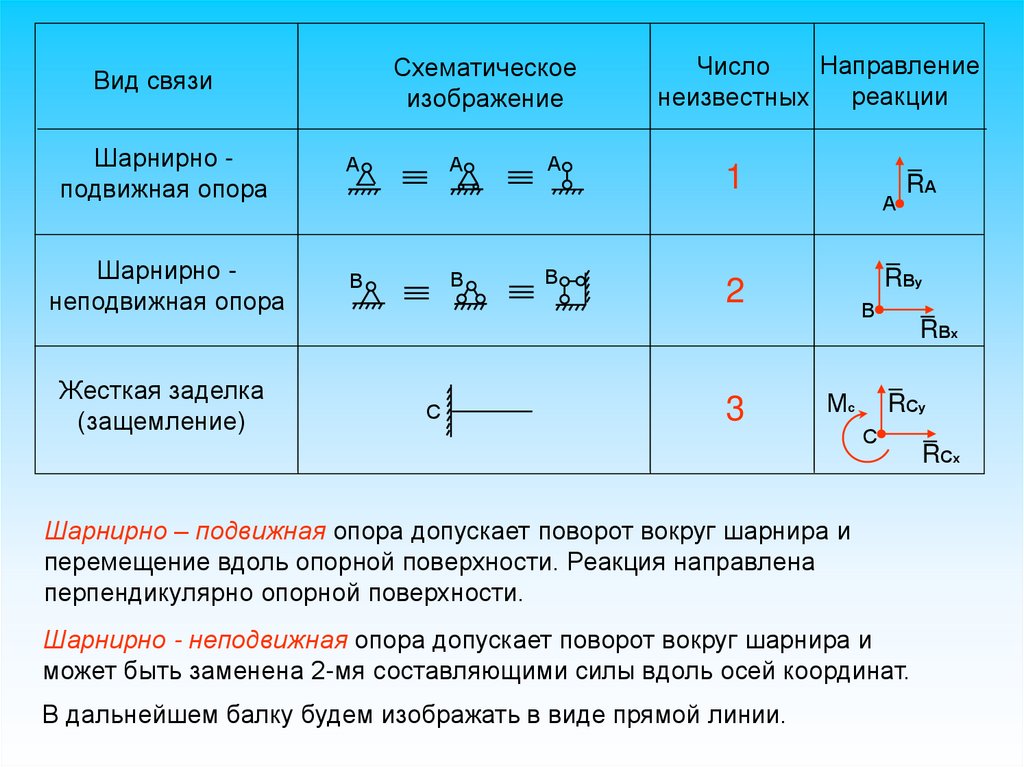
Схематическое
изображение
Вид связи
Шарнирно подвижная опора
А
Шарнирно неподвижная опора
В
Жесткая заделка
(защемление)
А
В
С
А
В
Направление
Число
реакции
неизвестных
1
А
RВу
2
3
RА
В
Мс
RВх
RСу
С
Шарнирно – подвижная опора допускает поворот вокруг шарнира и
перемещение вдоль опорной поверхности. Реакция направлена
перпендикулярно опорной поверхности.
Шарнирно - неподвижная опора допускает поворот вокруг шарнира и
может быть заменена 2-мя составляющими силы вдоль осей координат.
В дальнейшем балку будем изображать в виде прямой линии.
RСх

47.

Домашнее задание:
• [1] стр. 35-40,
• конспект,
• рабочая тетрадь стр.11-13