Трехшарнирные системы

1.

Тема лекции:
ТРЕХШАРНИРНЫЕ СИСТЕМЫ
Геометрически неизменяемая система, которая состоит из
двух жестких дисков, соединенных между собой шарниром C
и
прикрепленных
к
основанию
двумя
шарнирно
неподвижными опорами А и В называется трехшарнирной
системой.
Покажем
на
рисунках
трехшарнирных систем
два
возможных
варианта

2.

ТРЕХШАРНИРНЫЕ СИСТЕМЫ
1)
1
2)
2
C
1
C
f
f
A
B
l
2
B
A
l
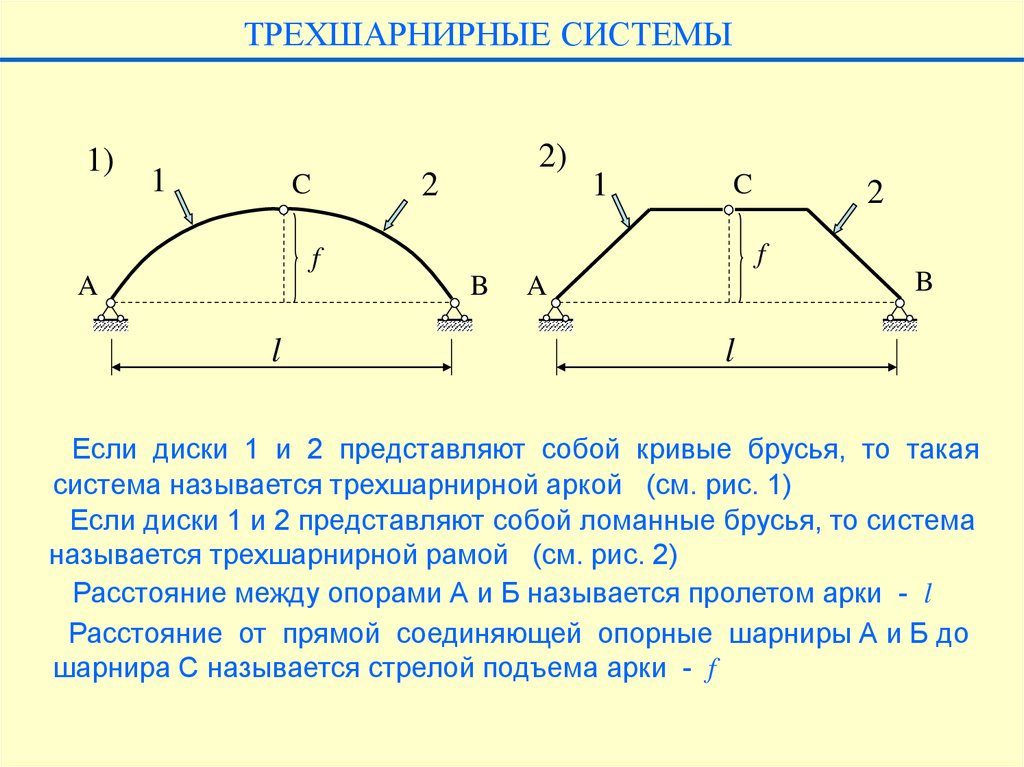
Если диски 1 и 2 представляют собой кривые брусья, то такая
система называется трехшарнирной аркой (см. рис. 1)
Если диски 1 и 2 представляют собой ломанные брусья, то система
называется трехшарнирной рамой (см. рис. 2)
Расстояние между опорами А и Б называется пролетом арки - l
Расстояние от прямой соединяющей опорные шарниры А и Б до
шарнира С называется стрелой подъема арки - f

3.

ТРЕХШАРНИРНЫЕ СИСТЕМЫ
а)
Ключ
б)
C
Пята
C
f
A
f
B
l
B
A
l
Шарниры А и В называются опорными или пятовыми шарнирами, а
шарнир С называется ключевым шарниром
Если 0,1≤ f/l ≤ 0,3 – арки называются пологими
Если 0,3< f/l ≤ 1,0 – арки называются повышенными
Трехшарнирные системы являются статически определимыми :
W=3D-2ШО-СОП=3·2-2·1-4=0,
и геометрически неизменямыми системами

4.

ТРЕХШАРНИРНЫЕ СИСТЕМЫ
1)
Р
2)
C
VА
C
VВ
f
f
A
B
НА
l
B
A
НВ
l
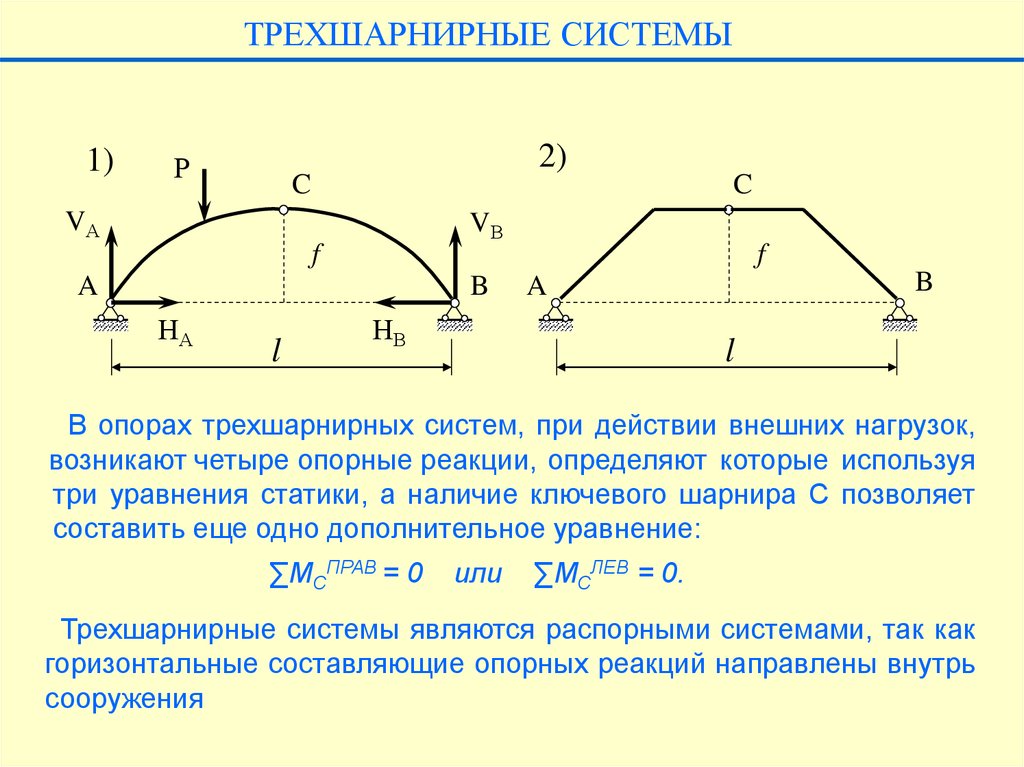
В опорах трехшарнирных систем, при действии внешних нагрузок,
возникают четыре опорные реакции, определяют которые используя
три уравнения статики, а наличие ключевого шарнира С позволяет
составить еще одно дополнительное уравнение:
∑МСПРАВ = 0
или
∑МСЛЕВ = 0.
Трехшарнирные системы являются распорными системами, так как
горизонтальные составляющие опорных реакций направлены внутрь
сооружения

5.

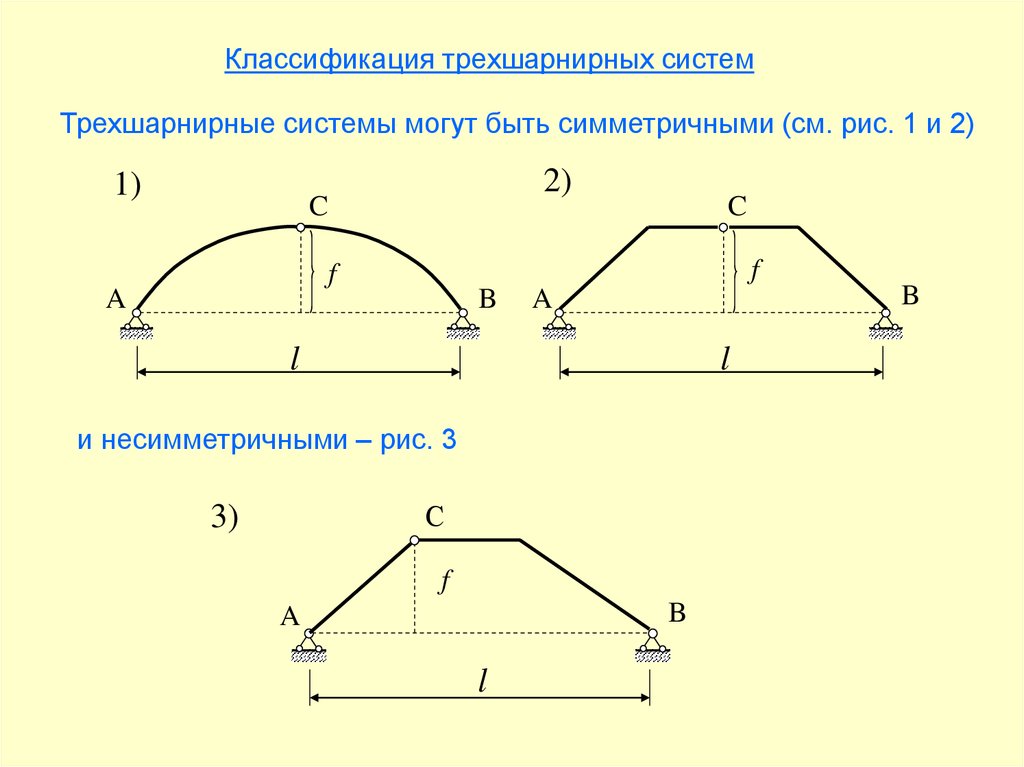
Классификация трехшарнирных систем
Трехшарнирные системы могут быть симметричными (см. рис. 1 и 2)
1)
2)
C
C
f
f
A
B
A
l
l
и несимметричными – рис. 3
С
3)
f
B
A
l
B

6.

Классификация трехшарнирных систем
Опорные шарниры А и В могут располагаться в одном уровне
(см.рис. 1,2,3) и могут располагаться в разных уровнях (рис. 4) – такие
системы называются ползучими арками или рамами
4)
C
f
B
ΔН
A
l

7.

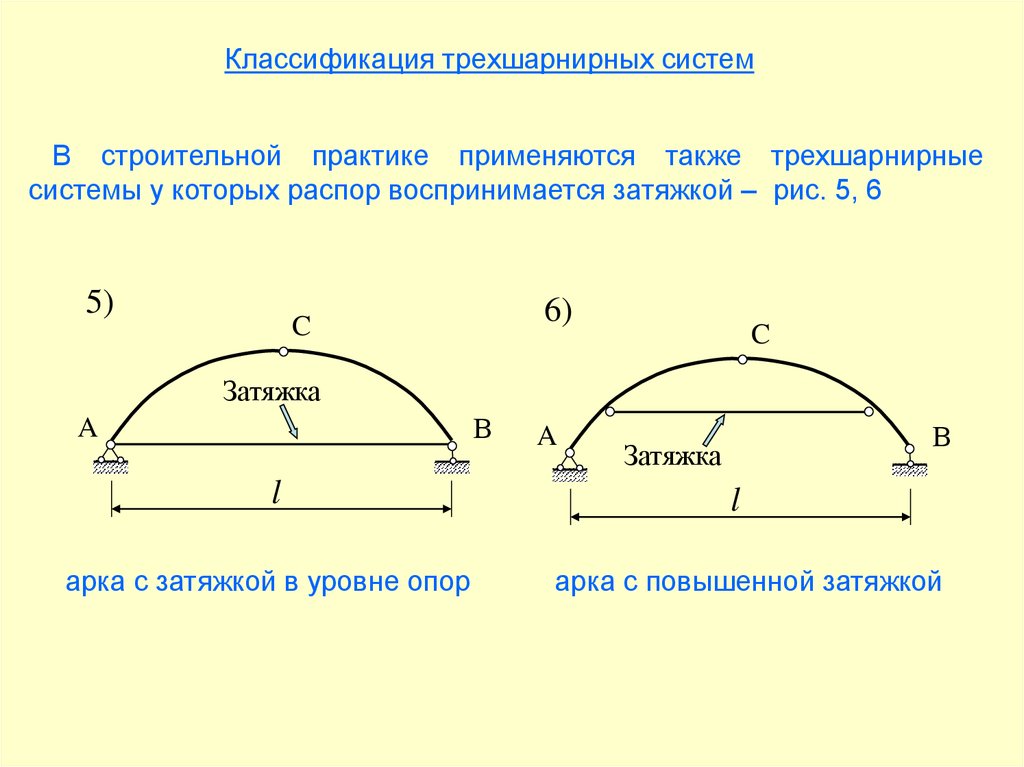
Классификация трехшарнирных систем
В строительной практике применяются также трехшарнирные
системы у которых распор воспринимается затяжкой – рис. 5, 6
5)
6)
C
C
Затяжка
В
A
l
арка с затяжкой в уровне опор
A
В
Затяжка
l
арка с повышенной затяжкой

8.

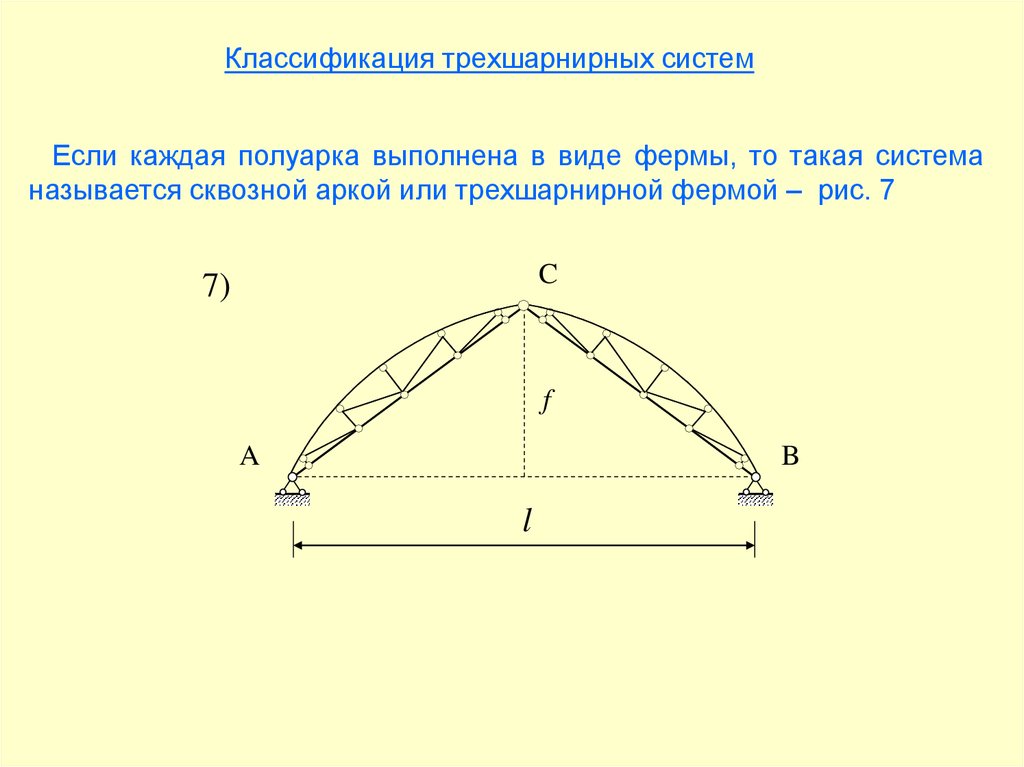
Классификация трехшарнирных систем
Если каждая полуарка выполнена в виде фермы, то такая система
называется сквозной аркой или трехшарнирной фермой – рис. 7
C
7)
f
A
B
l

9.

Расчет трехшарнирных арок на неподвижные нагрузки
у
Очертание оси арки y=f(x) задано
x
a1
Р1
VA
(x)
A
VA0
Р2
C
y(x)
HB
l/2
l/2
A0
x
VB
B
f
HA
a1
a2
Р1
Р2
C0
a2
VB
∑МА=0; =>
VB = VB0
∑МB=0; =>
VA = VA0
x ∑X=0; => HA = HB = H
∑МCлев=0; или ∑МСправ =0;
0
B0
l
1. Опорные реакции
=>
Н=МС0/ f .
2. Внутренние усилия
Покажем на оси арки сечение, расположенное на расстоянии X от
левой опоры
y(x) – расстояние по вертикали от оси х до сечения, (х) – угол
наклона касательной, проведенной к сечению к оси х
Для определения внутренних усилий рассмотрим часть арки и
балочной аналогии, расположенной левее сечения

10.

Расчет трехшарнирных арок на неподвижные нагрузки
(x)
у
M(x)=VA·x – P1·(x-a1) - H·y(x)
x
a1
Р1
VA
A
(x)
Изгибающие моменты в сечениях арки
M0(x)
Тогда, в общем виде:
y(x)
M(x)=M0(x)- H·y(x)
H
x
VA0
a1
Поперечные силы в сечениях арки
Q(x)=(VA – P1 )·cos - H·sin
Р1
A0
x
(1)
Q0(x)
Или в общем виде:
Q(x)=Q0(x)·cos - H·sin
(2)
Продольные силы в сечениях арки
N(x)= -(VA – P1 )·sin - H·cos
Q0(x)
Или в общем виде:
N(x)= -Q0(x)·sin - H·cos (3)

11.

Построение эпюр в трехшарнирных арках
Для построения эпюр в трехшарнирных арках поступают
следующим образом.
Арку разбивают на достаточное число участков (10-15 в
зависимости от требуемой точности расчета) и в соответствии с
формулами (1), (2), (3) определяют внутренние усилия М, Q и N во
всех сечениях, на границах участков.
По полученным значениям усилий строят соответствующие
эпюры.
Не зависимо от внешних нагрузок эпюры М, Q и N в арках
криволинейны, поскольку ось арки и угол наклона касательной по
длине пролета изменяются нелинейно .
В местах приложения сосредоточенных сил в эпюре Q получаем
скачок на величину P·cos , а на эпюре N - скачок P·sin .

12.

Арка рационального очертания
Вид эпюр и значения величин внутренних усилий в арках зависят
от очертания оси арки.
Для заданного вида нагрузки можно подобрать такое очертание
оси арки, что изгибающие моменты М и поперечные силы Q в любом
ее сечении будут равны нулю.
Такая арка и называется аркой рационального очертания.
Пример:
Пусть трехшарнирная арка пролетом l и стрелой подъема f
загружена по всей длине пролета равномерно-распределенной
нагрузкой q.
Необходимо подобрать очертание оси арки, при котором М и Q в
любом ее сечении будут равны нулю.

13.

Арка рационального очертания
q
у
C
VA
A
f
H
H
VB
q
0
A0
x
x
l/2
l/2
VA0
VB
B
B0
l
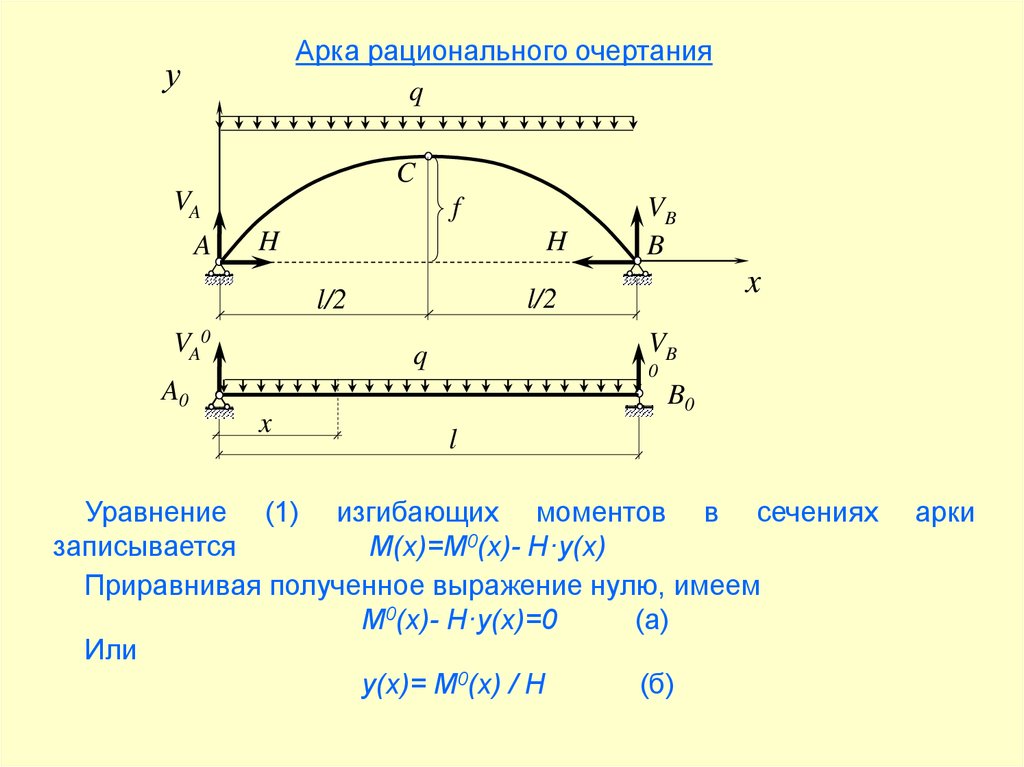
Уравнение (1) изгибающих моментов в сечениях
записывается
M(x)=M0(x)- H·y(x)
Приравнивая полученное выражение нулю, имеем
M0(x)- H·y(x)=0
(а)
Или
y(x)= M0(x) / H
(б)
арки

14.

Арка рационального очертания
q
у
C
VA
A
f
H
H
VB
q
0
A0
x
x
l/2
l/2
VA0
VB
B
B0
l
M0(x)=(ql/2) x – qx2/2 = (q/2)·x (l - x)
M0C = (ql)/2 l/2 - (ql)/2 l/4 = ql2/8
H = M0C / f = (ql2)/(8f)
Подставляя полученные значения M0(x) и Н в (б), получаем
уравнение оси арки рационального очертания
y(x) = (4f /l2)·x(l - x)

15.

Особенности расчета арок с затяжками
1. Рассмотрим арку с затяжкой в уровне опор
Р
C
VА
A
VВ
NЗ
В
l
f
При действии на такую арку
внешних нагрузок, в опорах
возникают только вертикальные составляющие опорных
реакций.
Их определяют с помощью
уравнений статики
∑МА=0; => VB ; ∑МВ=0; => VА
Для определения усилия в затяжке, проводят сечение через
шарнир С и затяжку.
И записывая одно из уравнений в виде ∑МСЛЕВ =0 или ∑МСПРАВ =0
определяют усилие в затяжке NЗ .

16.

Особенности расчета арок с затяжками
1. Рассмотрим арку с затяжкой в уровне опор
Р
C
VА
A
VВ
NЗ
f
В
l
Внутренние усилия в сечениях арки с затяжкой определяют по тем
же формулам (1) – (3) что и в обычных арках, только вместо распора
Н принимают усилие в затяжке NЗ
M(x)=M0(x)- NЗ·y(x)
Q(x)=Q0(x)·cos - NЗ·sin
N(x)= -Q0(x)·sin - NЗ·cos

17.

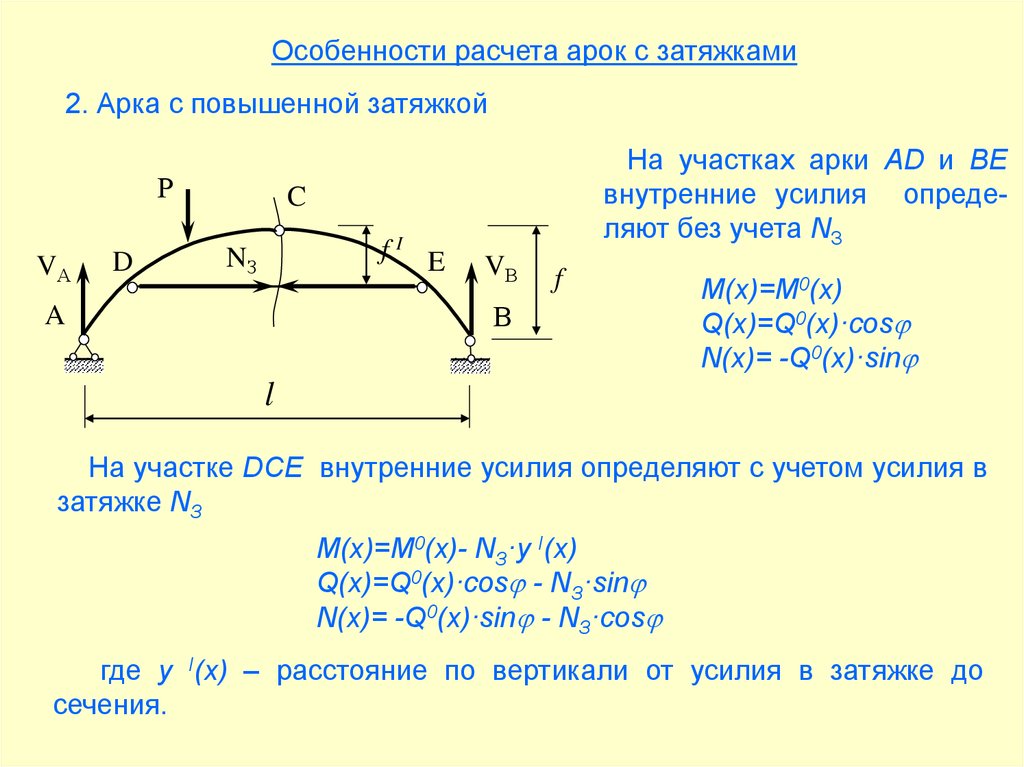
Особенности расчета арок с затяжками
2. Арка с повышенной затяжкой
Р
VА
C
fI
NЗ
VВ
В
A
l
f
В арках с повышенной
затяжкой в опорах так же
возникают только вертикальные составляющие опорных
реакций.
Их определяют с помощью
уравнений статики
∑МА=0; => VB ; ∑МВ=0; => VА
Для определения усилия в затяжке, проводят сечение через
шарнир С и затяжку.
Записывая уравнение в виде ∑МСЛЕВ =0 или
∑МСПРАВ =0
определяют усилие в затяжке NЗ .

18.

Особенности расчета арок с затяжками
2. Арка с повышенной затяжкой
Р
VА
D
На участках арки AD и BЕ
внутренние усилия определяют без учета NЗ
C
fI E
NЗ
VВ
f
В
A
M(x)=M0(x)
Q(x)=Q0(x)·cos
N(x)= -Q0(x)·sin
l
На участке DCЕ внутренние усилия определяют с учетом усилия в
затяжке NЗ
M(x)=M0(x)- NЗ·y I(x)
Q(x)=Q0(x)·cos - NЗ·sin
N(x)= -Q0(x)·sin - NЗ·cos
где y I(x) – расстояние по вертикали от усилия в затяжке до
сечения.

19.

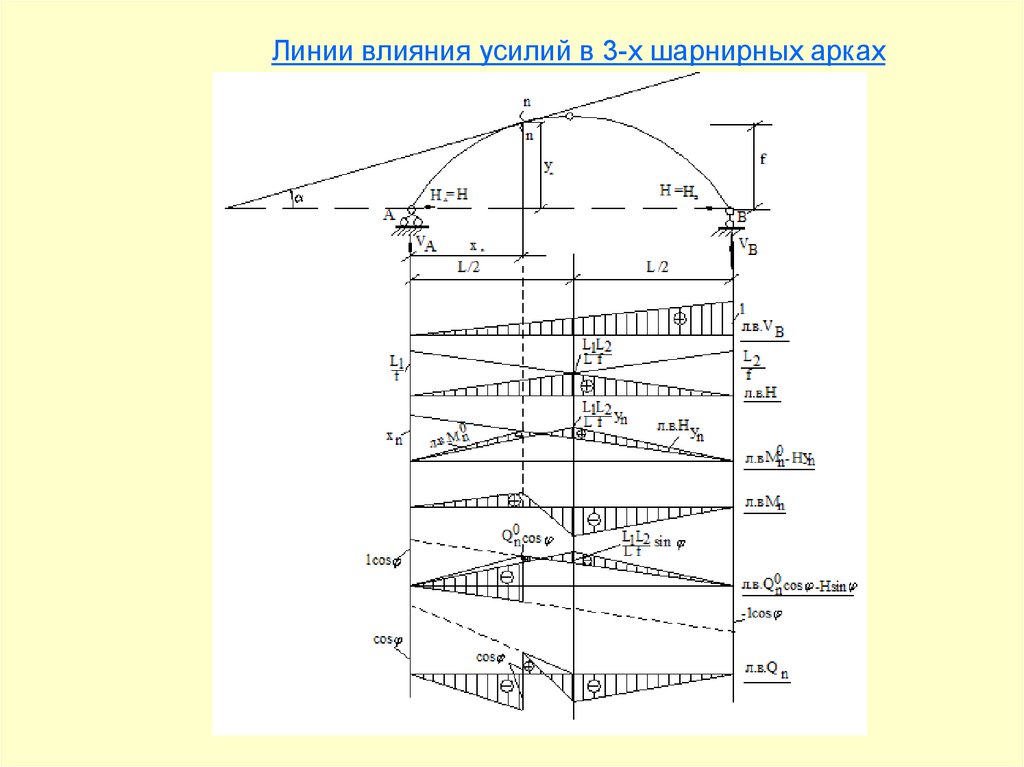
Линии влияния усилий в 3-х шарнирных арках

20.

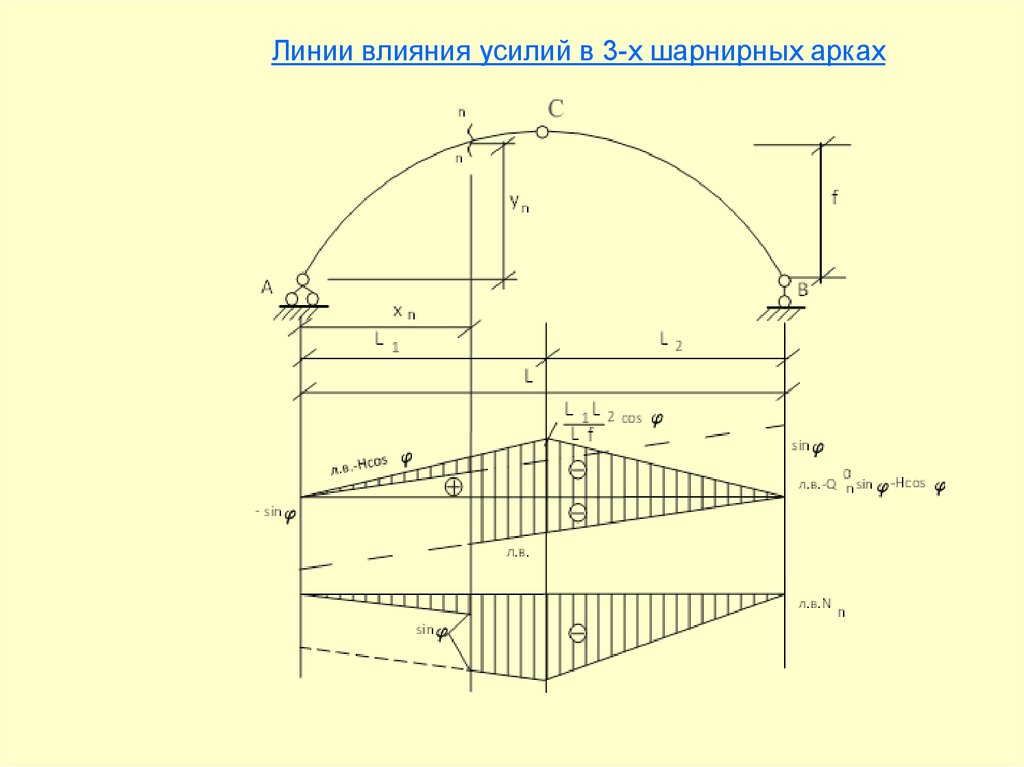
Линии влияния усилий в 3-х шарнирных арках

21.

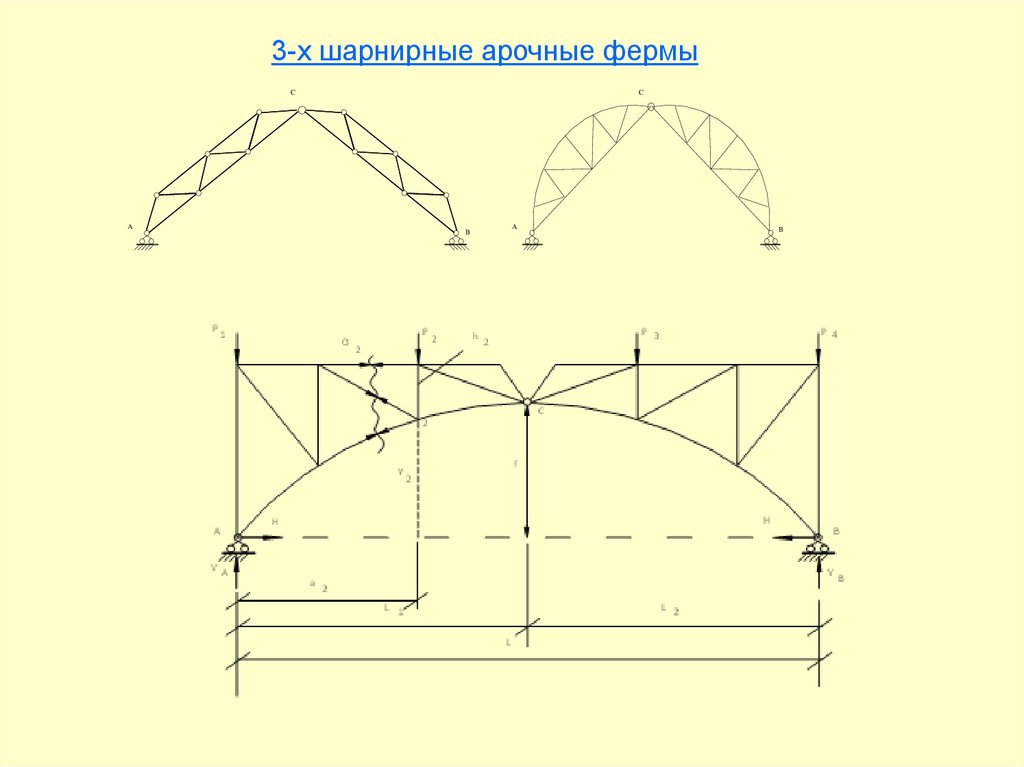
3-х шарнирные арочные фермы
C
A
C
B
A
B

22.

Статически определимые комбинированные системы