Методы комплексных сравнений многопараметрических объектов в научных исследованиях в сельском и лесном хозяйстве

1.

Нижегородская государственная
сельскохозяйственная академия
Факультет лесного хозяйства
Методы комплексных сравнений
многопараметрических объектов в научных
исследованиях в сельском и лесном хозяйстве
Бессчетнов В.П.
E-mail: lesfak@bk.ru.

2.

Вопросы
• 1. Проблемы применения методов
комплексной сравнительной оценки
• 2. Теоретические основы метода
• 3. Алгоритмы вычисления обобщенных
расстояний
• 4. Техника применения метода
• 5. Реализация метода в электронных
таблицах (Excel, SPSS, STATISTICA)

3.

Ключевые слова: многомерные объекты,
многопараметрические объекты,
векторное пространство, евклидово
пространство, декартовы координаты,
линейное расстояние, евклидово
расстояние, расстояние Махаланобиса,
признаки непосредственного учета,
производные признаки.

4.

1. Проблемы применения
методов комплексной
сравнительной оценки

5.

Схема замеров линейных параметров шишки
сосны обыкновенной

6.

Шишки разных плюсовых деревьев сосны обыкновенной

7.

- признак 1 – длина шишки (Н);
- признак 2 – боковое расстояние (L1);
- признак 3 – максимальный диаметр шишки (d);
- признак 4 – масса шишки (M);
- признак 5 – осевое расстояние (hК): hК=(L12 – r2)1/2;
- признак 6 – отношение длины к максимальному диаметру (ОHd): ОHd = H/d;
- признак 7 – отношение осевого расстояния к максимальному диаметру
(ОhKd): ОhKd = hК/d (двойной тангенс угла наклона линии бокового расстояния);
- признак 8 – отношение длины к боковому расстоянию (ОHL): ОHL =H/L1;
- признак 9 – отношение высоты основания к радиусу (тангенс угла наклона);
- признак 10 – высота основания (hC): hC=Н – hК;
- признак 11 – отношение высоты основания шишки к осевому расстоянию;
- признак 12 – объем конуса (VК): VК = 1/3×π×r2×hК объем;
- признак 13 – объем шарового сегмента (VC): VC=π×hC2×(3×r - hC)/3;
- признак 14 – суммарный объем конуса и сегмента (V): V= VК+VС;
- признак 15 – отношение массы к объему конуса и сегмента (КП): КП= V/М;
- признак 16 – линейно распределенная масса шишки (LМ): LМ=М/ L;
- признак 17 – отношение объемов сегмента и конуса (ОV): ОV= VC /VК.

8.

Измерение линейных параметров и массы шишек

9.

Дисперсионный анализ – это одно из ярчайших и выдающихся
достижений научной методологии, один из эффективнейших
инструментов исследований, введение которого в 1925 году Р.Э.
Фишером по своей значимости можно сравнить с изобретением
микроскопа А. ван Левенгуком
Сэр Рональд Эйлмер Фишер (англ. Sir Ronald Aylmer Fisher, 17 февраля
1890 — 29 июля 1962) — английский статистик, биолог-эволюционист и
генетик. Андерс Халд охарактеризовал его как «гения, едва не в одиночку
заложившего основы современной статистики», а Ричард Докинз назвал
«величайшим биологом, подобным Дарвину».
Антони ван Ле́венгук (Antoni van Leeuwenhoek, Thonius Philips van
Leeuwenhoek; 24 октября 1632, Делфт — 26 августа 1723, Делфт) —
нидерландский натуралист, конструктор микроскопов, основоположник
научной микроскопии, исследовавший с помощью своих микроскопов
структуру различных форм живой материи.

10.

2. Теоретические основы
метода

11.

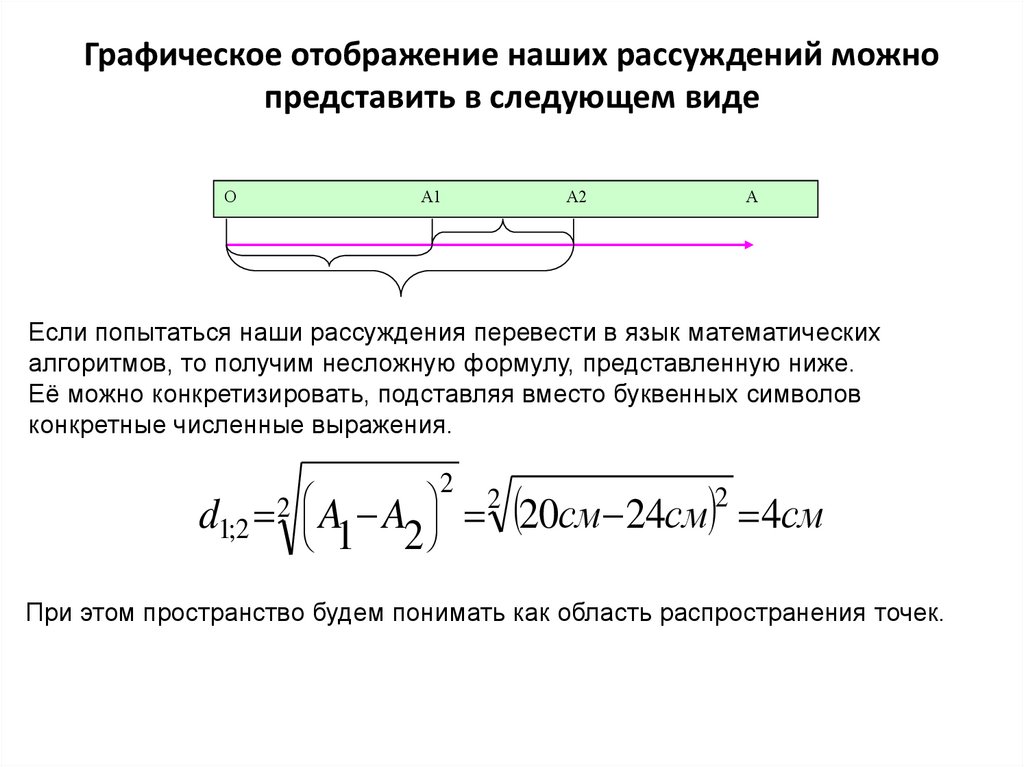
Графическое отображение наших рассуждений можно
представить в следующем виде
О
А1
А2
А
Если попытаться наши рассуждения перевести в язык математических
алгоритмов, то получим несложную формулу, представленную ниже.
Её можно конкретизировать, подставляя вместо буквенных символов
конкретные численные выражения.
d1;2 2 A A
2
1
2
20см 24см 4см
2
2
При этом пространство будем понимать как область распространения точек.

12.

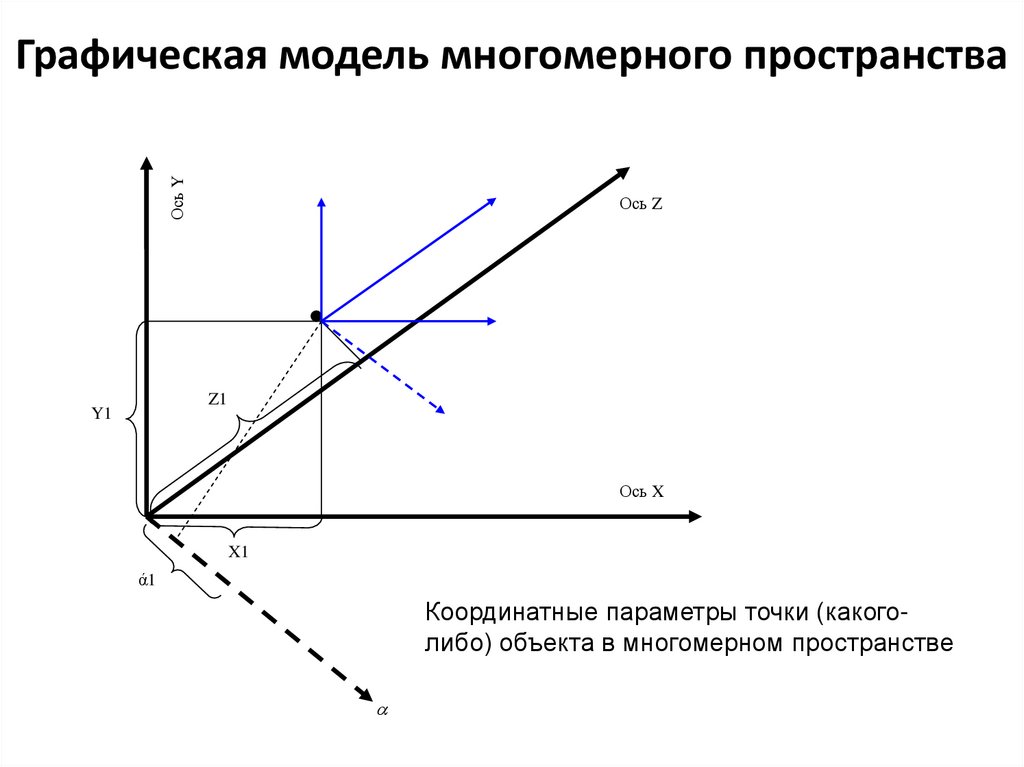
Ось Y
Графическая модель многомерного пространства
Ось Z
Z1
Y1
Ось X
X1
ά1
Координатные параметры точки (какоголибо) объекта в многомерном пространстве

13.

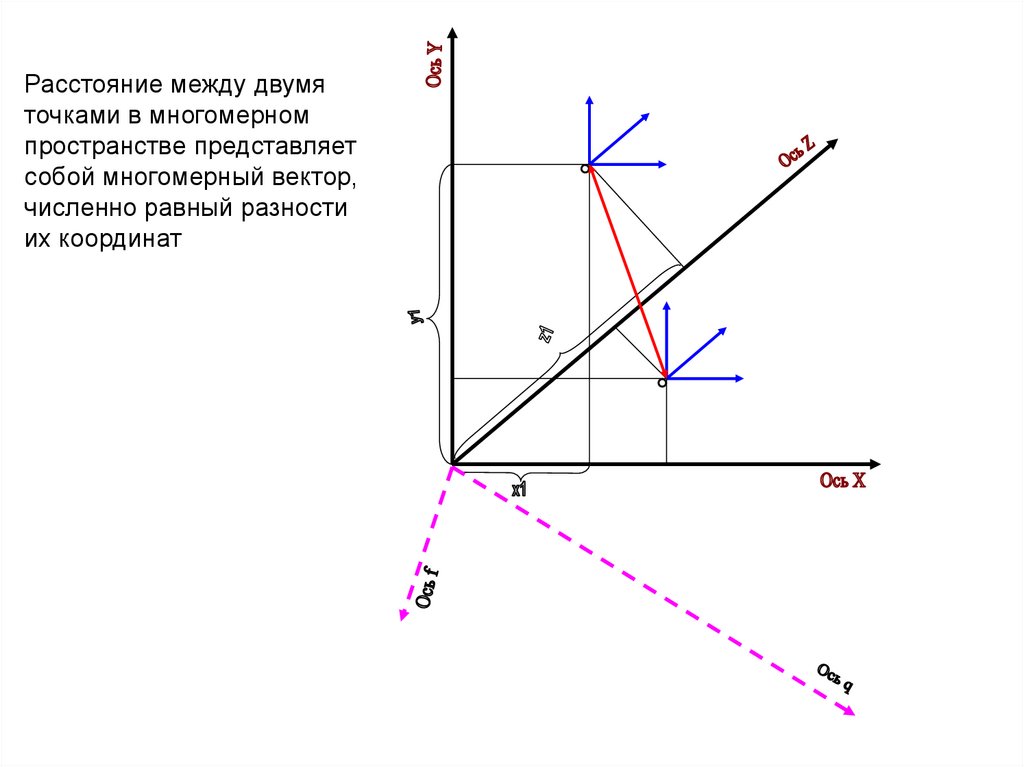
Расстояние между двумя
точками в многомерном
пространстве представляет
собой многомерный вектор,
численно равный разности
их координат

14.

ВЕКТОРНОЕ ПРОСТРАНСТВО – это
математическое понятие,
обобщающее понятие совокупности
всех свободных векторов 3-х мерного
(в общем случае, многомерного)
пространства (на случай
произвольного числа наблюдений).

15.

ЕВКЛИДОВО ПРОСТРАНСТВО – это
пространство, свойства которого
изучаются в евклидовой
геометрии. В более широком
понимании евклидовым
пространством называют n-мерное
векторное пространство, в
котором определено скалярное
произведение векторов.

16.

В более общем смысле евклидовым пространством называется
n-мepное векторное пространство, в котором возможно ввести
некоторые специальные координаты (декартовы) так, что метрика
его будет определена следующим образом: если точка М имеет
координаты (х1, х2,..., xn), а точка М* — координаты (x1*, x2*,...,
xn*), то расстояние между этими точками будет:
МНОГОМЕРНОЕ ПРОСТРАНСТВО – это пространство, имеющее число
измерений (размерность) более трёх. Обычное евклидово пространство,
изучаемое в элементарной геометрии, трёхмерно; плоскости — двумерны,
прямые линии — одномерны.

17.

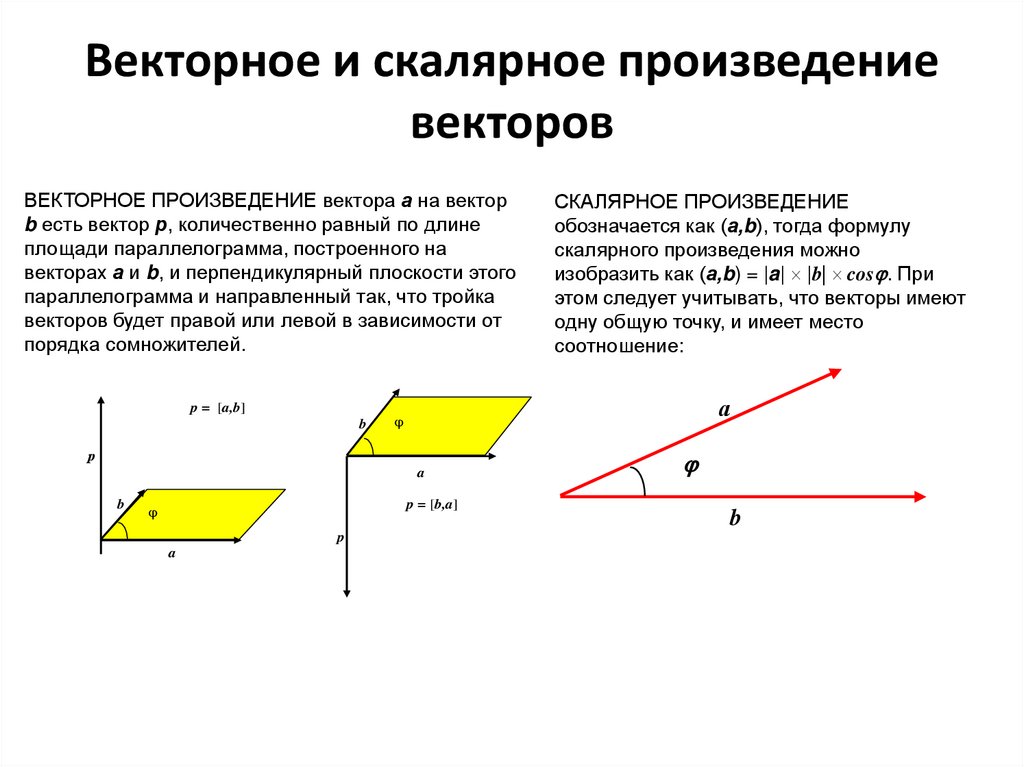
Векторное и скалярное произведение
векторов
ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ вектора а на вектор
b есть вектор р, количественно равный по длине
площади параллелограмма, построенного на
векторах а и b, и перпендикулярный плоскости этого
параллелограмма и направленный так, что тройка
векторов будет правой или левой в зависимости от
порядка сомножителей.
p = [a,b]
b
а
р
a
b
p = [b,a]
p
a
СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ
обозначается как (а,b), тогда формулу
скалярного произведения можно
изобразить как (а,b) = |a| |b| cos . При
этом следует учитывать, что векторы имеют
одну общую точку, и имеет место
соотношение:
b

18.

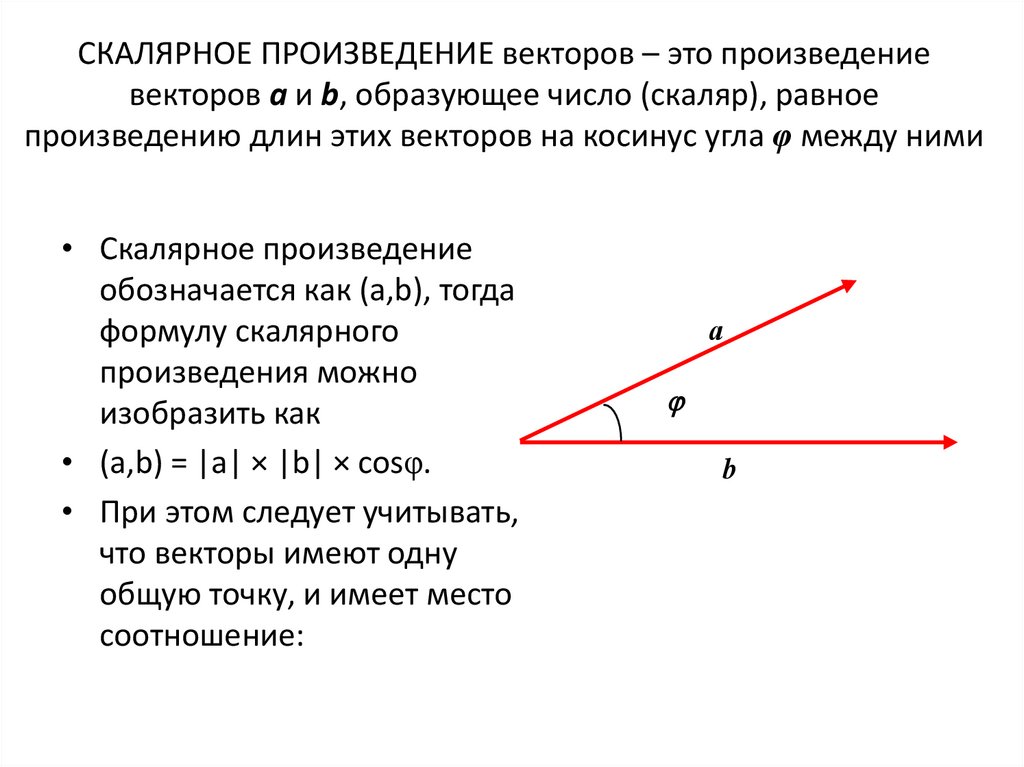
СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ векторов – это произведение
векторов а и b, образующее число (скаляр), равное
произведению длин этих векторов на косинус угла φ между ними
• Скалярное произведение
обозначается как (а,b), тогда
формулу скалярного
произведения можно
изобразить как
• (а,b) = |a| × |b| × cosφ.
• При этом следует учитывать,
что векторы имеют одну
общую точку, и имеет место
соотношение:
а
b

19.

Практическая реализация многомерного
анализа базируется на ряде условий:
• анализируемых признаков может быть неограниченное
количество (на современном этапе развития теоретических
положений метода это однозначно не определено);
• все объекты должны характеризоваться одним и тем же
набором параметров (признаков), т.е. должны располагаться в
едином многомерном пространстве, каждая точка которого
описывается одним и тем же набором координат;
• относительно каждого из признаков существует возможность
вычисления оценок корреляции и ковариации со всеми
остальными признаками в многомерном комплексе сравнения;
• объекты, носители признаков, должны иметь некоторую
логическую общность и системность характеристик;
• используемые в анализе признаки должны быть представлены
количественной оценкой (скалярными величинами).

20.

3. Алгоритмы вычисления
обобщенных расстояний

21.

Расстоянием (метрикой) между объектами в многомерном
пространстве признаков признается такая величина dab,
которая удовлетворяет следующим условиям:
• dab > 0, (объект а не есть объект b, их
координаты не совпадают хотя бы по
одному из координатных параметров)
• daa = 0;
• dab = dba;
• dab + dbc ≥ dac (однако это требование не
является конструктивным и практически
никогда не учитывается в расчетах).

22.

Мерой близости (сходства) объектов в многомерном
пространстве называется величина μab, которая имеет
предел и возрастает с возрастанием близости объектов; она
должна удовлетворять следующим условиям:
• μab – непрерывна, т.е. малому изменению
положения точек в пространстве отвечает
малое изменение меры;
• μab = μba;
• 0 ≤ μab ≤ 1; μab = 1 ↔ a = b (если a = b).

23.

Переход от оценок взаимного расположения объектов в
пространстве (и, следовательно, оценок степени их
близости или отдаленности) по расстоянию между
объектами к оценкам в мерах близости осуществляется
посредством достаточно простого преобразования
посредством потенциальной функции:
μab = 1/(1+ dab).
Существуют достаточно адекватные статистики для
измерения расстояния между объектами в пространстве
m признаков. Некоторые из них приведены ниже.

24.

1. Линейное расстояние:
• dLij = Σ │xil – xjl │ = Σ │xi – xj │l
l=1,m (ниже приведена запись в матричной форме)
d
xi x j Tl xi x j l bi b j Tl bi b j
l
Lij
xil – нормированное значение l-го признака у i-го объекта;
xjl – нормированное значение l-го признака у j-го объекта;
l = 1, m – индекс признака, принимает значение 1, 2, 3, …m;
i = 1, n – индекс одного из сравниваемых объектов, принимает
значение 1, 2, 3, … n ;
j = 1, n – индекс второго из сравниваемых объектов, принимает
значение 1, 2, 3, … n ;
m – количество признаков, определяющее мерность пространства;
n – количество объектов сравниваемых между собой в многомерном
пространстве признаков;
xi – матрица-столбец значений всех признаков от 1 до m на i-м объекте;
xj – матрица-столбец значений всех признаков от 1 до m на j-м
объекте.

25.

2. Евклидово расстояние:
• dEij = Σ xil – xjl 2 1/2 = Σ xi – xj l2 1/2
l=1,m (ниже приведена запись в матричной форме)
d
Еij
xi x j Tl xi x j l bi b j Tl bi b j l
xil – нормированное значение l-го признака у i-го объекта;
xjl – нормированное значение l-го признака у j-го объекта;
l = 1, m – индекс признака, принимает значение 1, 2, 3, …m;
i = 1, n – индекс одного из сравниваемых объектов, принимает значение
1, 2, 3, … n ;
j = 1, n – индекс второго из сравниваемых объектов, принимает значение
1, 2, 3, … n ;
m – количество признаков, определяющее мерность пространства;
n – количество объектов сравниваемых между собой в многомерном
пространстве признаков;
xi – матрица-столбец значений всех признаков от 1 до m на i-м объекте;
xj – матрица-столбец значений всех признаков от 1 до m на j-м объекте.

26.

3. Квадрат евклидова расстояния:
• d2Eij = Σ xil – xjl 2 = Σ xi – xj l2
l=1,m (ниже приведена запись в матричной форме)
d
Еij
2 xi x j T xi x j bi b j T bi b j
l
l
l
xil – нормированное значение l-го признака у i-го объекта;
xjl – нормированное значение l-го признака у j-го объекта;
l = 1, m – индекс признака, принимает значение 1, 2, 3, …m;
i = 1, n – индекс одного из сравниваемых объектов, принимает значение
1, 2, 3, … n ;
j = 1, n – индекс второго из сравниваемых объектов, принимает значение
1, 2, 3, … n ;
m – количество признаков, определяющее мерность пространства;
n – количество объектов сравниваемых между собой в многомерном
пространстве признаков;
xi – матрица-столбец значений всех признаков от 1 до m на i-м объекте;
xj – матрица-столбец значений всех признаков от 1 до m на j-м объекте.

27.

Соотношение между линейным
расстоянием и евклидовой дистанцией:
• d 2Lij = Σ │xi – xj │l2 или Σ (xi – xj )l2
• d2Eij = Σ xil – xjl 2 = Σ xi – xj l2
T
2 x x T x x
d Lij
b
b
i j l i j l i j l bi b j l
2 x x T x x
d Eij
i j l i j l bi b j Tl bi b j l
xil – нормированное значение l-го признака у i-го объекта;
xjl – нормированное значение l-го признака у j-го объекта;
l = 1, m – индекс признака, принимает значение 1, 2, 3, …m;
i = 1, n – индекс 1-го объекта, принимает значение 1, 2, 3, … n ;
j = 1, n – индекс 2-го объекта, принимает значение 1, 2, 3, … n ;
m – количество признаков, определяющее мерность пространства;
n – количество многопараметрических объектов;
xi – матрица-столбец значений всех признаков от 1 до m на i-м объекте;
xj – матрица-столбец значений признаков от 1 до m на j-м объекте.

28.

4. Расстояние Махаланобиса:
• dMij = xi – xj lT ×Wij-1 × xi – xj l
• l=1,m (применена матричная запись)
xil – нормированное значение l-го признака у i-го объекта;
xjl – нормированное значение l-го признака у j-го объекта;
l = 1, m – индекс признака, принимает значение 1, 2, 3, …m;
i = 1, n – индекс одного из сравниваемых объектов, принимает значение
1, 2, 3, … n ;
j = 1, n – индекс второго из сравниваемых объектов, принимает значение
1, 2, 3, … n ;
m – количество признаков, определяющее мерность пространства;
n – количество объектов сравниваемых между собой в многомерном
пространстве признаков;
xi – матрица-столбец значений всех признаков от 1 до m на i-м объекте;
xj – матрица-столбец значений всех признаков от 1 до m на j-м объекте.
W-1 – матрица обратная обобщенной ковариационной матрице для
данной пары объектов.

29.

4. Техника применения
метода

30.

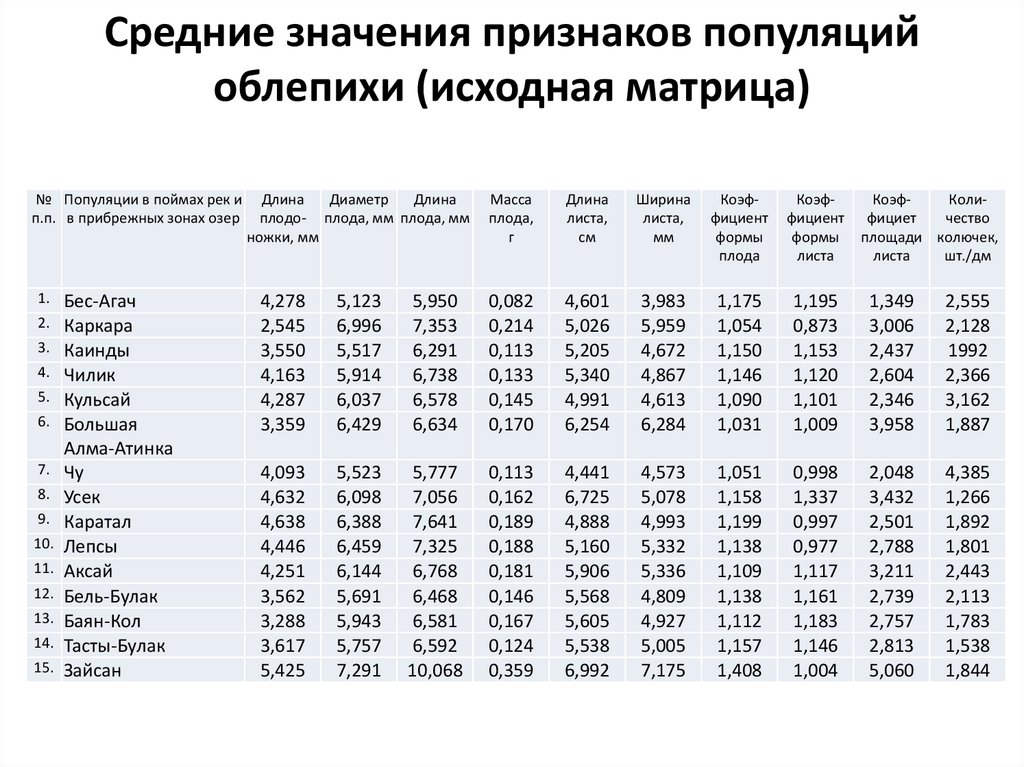
Средние значения признаков популяций
облепихи (исходная матрица)
№ Популяции в поймах рек и
п.п. в прибрежных зонах озер
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
Бес-Агач
Каркара
Каинды
Чилик
Кульсай
Большая
Алма-Атинка
Чу
Усек
Каратал
Лепсы
Аксай
Бель-Булак
Баян-Кол
Тасты-Булак
Зайсан
Длина
Диаметр
Длина
плодо- плода, мм плода, мм
ножки, мм
Масса
плода,
г
Длина
листа,
см
Ширина
листа,
мм
Коэффициент
формы
плода
Коэффициент
формы
листа
КоэфКолифициет
чество
площади колючек,
листа
шт./дм
4,278
2,545
3,550
4,163
4,287
3,359
5,123
6,996
5,517
5,914
6,037
6,429
5,950
7,353
6,291
6,738
6,578
6,634
0,082
0,214
0,113
0,133
0,145
0,170
4,601
5,026
5,205
5,340
4,991
6,254
3,983
5,959
4,672
4,867
4,613
6,284
1,175
1,054
1,150
1,146
1,090
1,031
1,195
0,873
1,153
1,120
1,101
1,009
1,349
3,006
2,437
2,604
2,346
3,958
2,555
2,128
1992
2,366
3,162
1,887
4,093
4,632
4,638
4,446
4,251
3,562
3,288
3,617
5,425
5,523
6,098
6,388
6,459
6,144
5,691
5,943
5,757
7,291
5,777
7,056
7,641
7,325
6,768
6,468
6,581
6,592
10,068
0,113
0,162
0,189
0,188
0,181
0,146
0,167
0,124
0,359
4,441
6,725
4,888
5,160
5,906
5,568
5,605
5,538
6,992
4,573
5,078
4,993
5,332
5,336
4,809
4,927
5,005
7,175
1,051
1,158
1,199
1,138
1,109
1,138
1,112
1,157
1,408
0,998
1,337
0,997
0,977
1,117
1,161
1,183
1,146
1,004
2,048
3,432
2,501
2,788
3,211
2,739
2,757
2,813
5,060
4,385
1,266
1,892
1,801
2,443
2,113
1,783
1,538
1,844

31.

В качестве исходного материала используется матрица
средних значений, представленная разноразмерными
и безразмерными неравнозначными величинами,
характеризующими объект, например популяцию,
экотип, сорта растений, породы животных, плюсовые
деревья на ЛСП и т.п. (табл. 1). Особенностью метода
является возможность использования в расчетах
статистических комплексов, состоящих только из
однородных величин, что наиболее удобно
представлять в форме их нормированных
безразмерных значений.
Принципиально, нормирование и приведение данных
(дат) к сопоставимому безразмерному виду возможно
с применением достаточно многочисленного набора
алгоритмов. В качестве примера они приведены ниже.

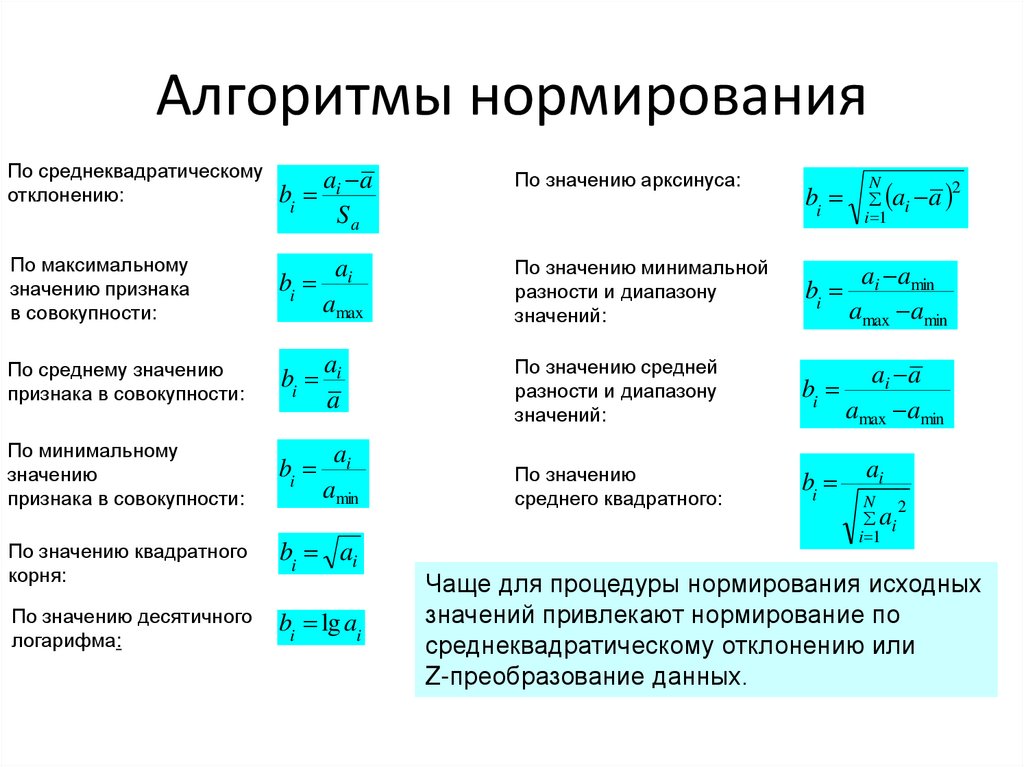
32.

Алгоритмы нормирования
По среднеквадратическому
отклонению:
bi
ai a
Sa
По значению арксинуса:
По максимальному
значению признака
в совокупности:
bi
ai
amax
По значению минимальной
разности и диапазону
значений:
bi
ai amin
amax amin
По среднему значению
признака в совокупности:
bi
ai
a
По значению средней
разности и диапазону
значений:
bi
ai a
amax amin
По минимальному
значению
признака в совокупности:
bi
ai
amin
По значению
среднего квадратного:
bi
По значению квадратного
корня:
bi ai
По значению десятичного
логарифма:
bi lg ai
bi
ai a 2
N
i 1
ai
N 2
ai
i 1
Чаще для процедуры нормирования исходных
значений привлекают нормирование по
среднеквадратическому отклонению или
Z-преобразование данных.

33.

НОРМИРОВАНОЕ ОТКЛОНЕНИЕ - это важный статистический показатель,
позволяющий определять изменчивость признаков. С его помощью можно
выразить в относительных единицах (долях Sj ) отклонение каждого
конкретного члена совокупности (aij) от средней арифметической (Aj ).
Формула Z-преобразования данных для вычисления нормированного
отклонения достаточно проста:
bij
aij A j
, где:
Sj
i = 1,… n – индекс значения (порядковый номер) объекта, (популяции, экотипа
или т.п.);
j = 1,…k – индекс значения (порядковый номер) анализируемого признака;
bij – элемент матрицы нормированных значений;
aij – элемент матрицы исходных значений;
Aj – обобщенное среднее значение j – го признака;
Sj – обобщенное среднеквадратическое отклонение j – го признака;
n – количество сравниваемых объектов в комплексе сравнения (популяций,
экотипов, клоновых групп и т.д.);
k – количество анализируемых признаков, введенных в комплекс сравнения.

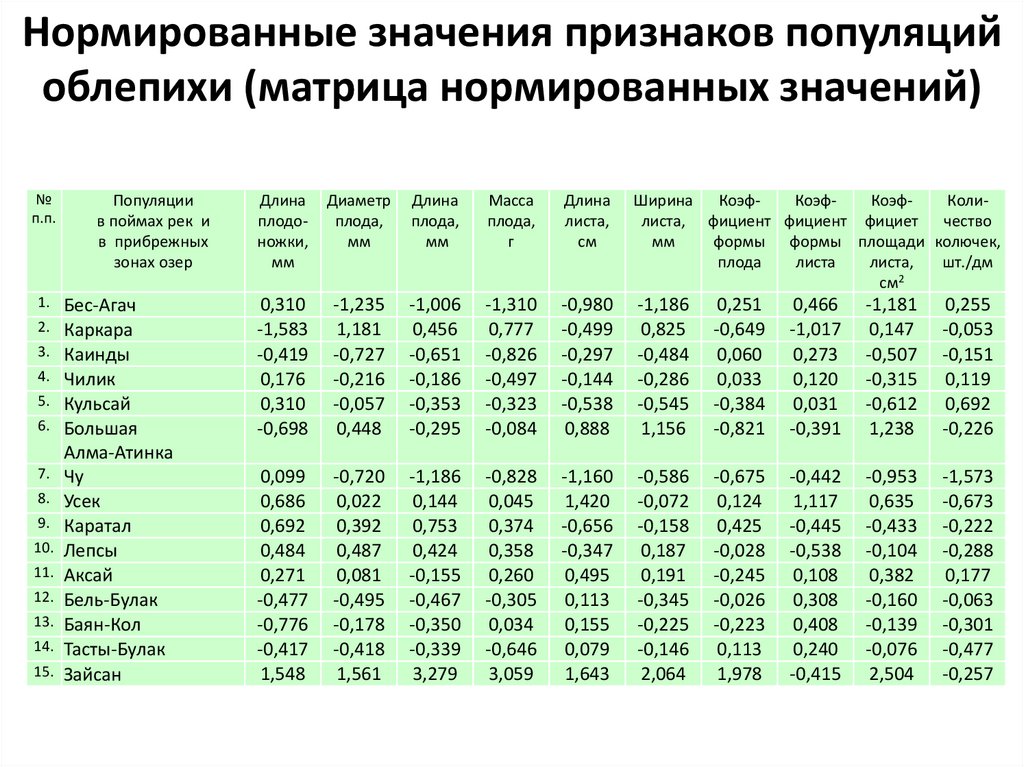
34.

Нормированные значения признаков популяций
облепихи (матрица нормированных значений)
№
п.п.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
Популяции
в поймах рек и
в прибрежных
зонах озер
Бес-Агач
Каркара
Каинды
Чилик
Кульсай
Большая
Алма-Атинка
Чу
Усек
Каратал
Лепсы
Аксай
Бель-Булак
Баян-Кол
Тасты-Булак
Зайсан
Длина
плодоножки,
мм
Диаметр
плода,
мм
Длина
плода,
мм
Масса
плода,
г
Длина
листа,
см
Ширина КоэфКоэфКоэфКолилиста, фициент фициент фициет чество
мм
формы формы площади колючек,
плода
листа
листа,
шт./дм
см2
0,310
-1,583
-0,419
0,176
0,310
-0,698
-1,235
1,181
-0,727
-0,216
-0,057
0,448
-1,006
0,456
-0,651
-0,186
-0,353
-0,295
-1,310
0,777
-0,826
-0,497
-0,323
-0,084
-0,980
-0,499
-0,297
-0,144
-0,538
0,888
-1,186
0,825
-0,484
-0,286
-0,545
1,156
0,251
-0,649
0,060
0,033
-0,384
-0,821
0,466
-1,017
0,273
0,120
0,031
-0,391
-1,181
0,147
-0,507
-0,315
-0,612
1,238
0,255
-0,053
-0,151
0,119
0,692
-0,226
0,099
0,686
0,692
0,484
0,271
-0,477
-0,776
-0,417
1,548
-0,720
0,022
0,392
0,487
0,081
-0,495
-0,178
-0,418
1,561
-1,186
0,144
0,753
0,424
-0,155
-0,467
-0,350
-0,339
3,279
-0,828
0,045
0,374
0,358
0,260
-0,305
0,034
-0,646
3,059
-1,160
1,420
-0,656
-0,347
0,495
0,113
0,155
0,079
1,643
-0,586
-0,072
-0,158
0,187
0,191
-0,345
-0,225
-0,146
2,064
-0,675
0,124
0,425
-0,028
-0,245
-0,026
-0,223
0,113
1,978
-0,442
1,117
-0,445
-0,538
0,108
0,308
0,408
0,240
-0,415
-0,953
0,635
-0,433
-0,104
0,382
-0,160
-0,139
-0,076
2,504
-1,573
-0,673
-0,222
-0,288
0,177
-0,063
-0,301
-0,477
-0,257

35.

Полученная матрица преобразованных
нормированных значений обладает
следующими свойствами:
- каждый
столбец (соответствует набору значений
нормированных показателей какого-либо признака у
разных объектов сравниваемого комплекса объектов –
популяций, экотипов, сортов, клонов и т.п.) имеет
нулевое среднее значение, т.е. сумма всех значений
нормированного показателя равна «нулю»: Мср = 0;
- среднеквадратическое отклонение нормированных
значений от их средней величины «0» равно
«единице»: СКО = 1.
Матрица нормированных значений используется для вычисления
обобщенного расстояния. Расчет обобщенного статистического
расстояния между реальными объектами при их попарном
сравнении будет иметь вид:

36.

Матрица нормированных значений используется для
вычисления обобщенного расстояния. Расчет обобщенного
статистического расстояния между реальными объектами
при их попарном сравнении будет иметь вид:
dij (bi1 b j1 ) (bi 2 b j 2 ) (bi3 b j 3 ) ... (bik b jk )
2
2
2
2
Получаемые в итоге такого анализа результаты, представляют собой систему
статистических оценок обобщенного расстояния в пределах каждой из
проанализированных пар объектов. Они неодинаковы, что соответствует
различной степени статистической удаленности или близости между
конкретными объектами, но при этом все полученные оценки сравнимы между
собой, поскольку получены для единого многомерного статистического
пространства, для одной и той же многомерной системы координат.

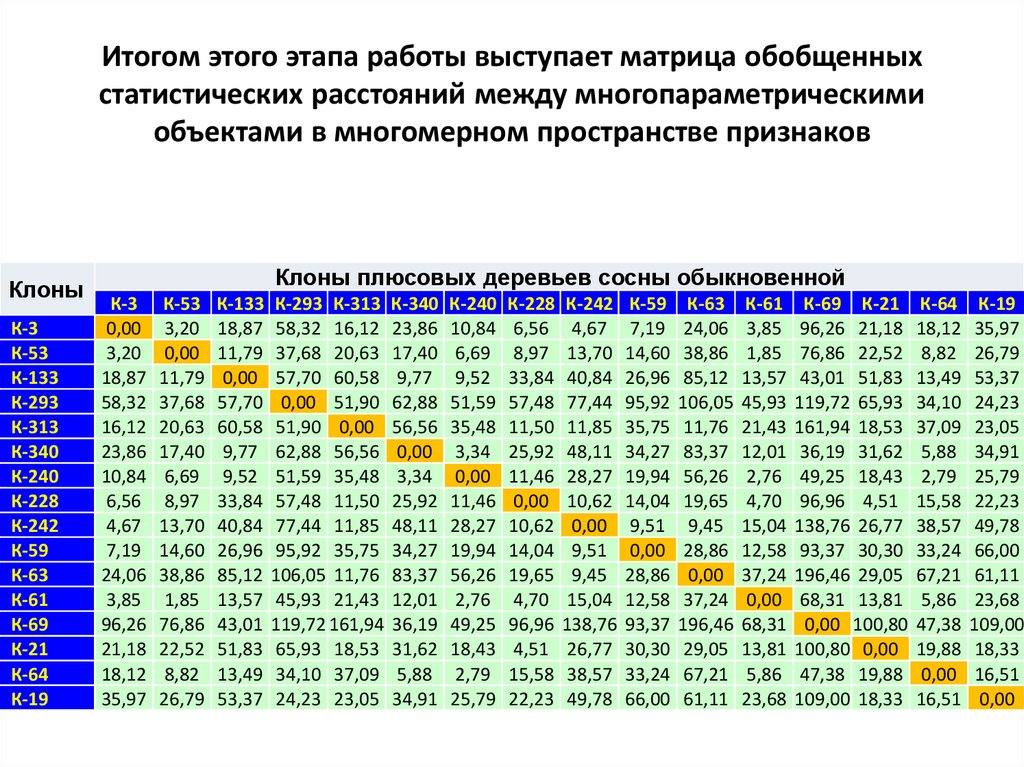
37.

Итогом этого этапа работы выступает матрица обобщенных
статистических расстояний между многопараметрическими
объектами в многомерном пространстве признаков
Клоны
К-3
К-53
К-133
К-293
К-313
К-340
К-240
К-228
К-242
К-59
К-63
К-61
К-69
К-21
К-64
К-19
Клоны плюсовых деревьев сосны обыкновенной
К-3
0,00
3,20
18,87
58,32
16,12
23,86
10,84
6,56
4,67
7,19
24,06
3,85
96,26
21,18
18,12
35,97
К-53
3,20
0,00
11,79
37,68
20,63
17,40
6,69
8,97
13,70
14,60
38,86
1,85
76,86
22,52
8,82
26,79
К-133
18,87
11,79
0,00
57,70
60,58
9,77
9,52
33,84
40,84
26,96
85,12
13,57
43,01
51,83
13,49
53,37
К-293 К-313
58,32 16,12
37,68 20,63
57,70 60,58
0,00 51,90
51,90 0,00
62,88 56,56
51,59 35,48
57,48 11,50
77,44 11,85
95,92 35,75
106,05 11,76
45,93 21,43
119,72 161,94
65,93 18,53
34,10 37,09
24,23 23,05
К-340
23,86
17,40
9,77
62,88
56,56
0,00
3,34
25,92
48,11
34,27
83,37
12,01
36,19
31,62
5,88
34,91
К-240
10,84
6,69
9,52
51,59
35,48
3,34
0,00
11,46
28,27
19,94
56,26
2,76
49,25
18,43
2,79
25,79
К-228
6,56
8,97
33,84
57,48
11,50
25,92
11,46
0,00
10,62
14,04
19,65
4,70
96,96
4,51
15,58
22,23
К-242
4,67
13,70
40,84
77,44
11,85
48,11
28,27
10,62
0,00
9,51
9,45
15,04
138,76
26,77
38,57
49,78
К-59
7,19
14,60
26,96
95,92
35,75
34,27
19,94
14,04
9,51
0,00
28,86
12,58
93,37
30,30
33,24
66,00
К-63
24,06
38,86
85,12
106,05
11,76
83,37
56,26
19,65
9,45
28,86
0,00
37,24
196,46
29,05
67,21
61,11
К-61
3,85
1,85
13,57
45,93
21,43
12,01
2,76
4,70
15,04
12,58
37,24
0,00
68,31
13,81
5,86
23,68
К-69 К-21
96,26 21,18
76,86 22,52
43,01 51,83
119,72 65,93
161,94 18,53
36,19 31,62
49,25 18,43
96,96 4,51
138,76 26,77
93,37 30,30
196,46 29,05
68,31 13,81
0,00 100,80
100,80 0,00
47,38 19,88
109,00 18,33
К-64
18,12
8,82
13,49
34,10
37,09
5,88
2,79
15,58
38,57
33,24
67,21
5,86
47,38
19,88
0,00
16,51
К-19
35,97
26,79
53,37
24,23
23,05
34,91
25,79
22,23
49,78
66,00
61,11
23,68
109,00
18,33
16,51
0,00

38.

Набор расстояний от одного объекта до всех остальных объектов
в многомерном комплексе сравнения называют
профилем данного объекта.
Клоны
К-3
Клоны плюсовых деревьев сосны обыкновенной
К-3
0,00
К-53 К-133 К-293 К-313 К-340 К-240 К-228 К-242 К-59 К-63 К-61 К-69 К-21 К-64 К-19
3,20 18,87 58,32 16,12 23,86 10,84 6,56 4,67 7,19 24,06 3,85 96,26 21,18 18,12 35,97
Принципиально это создает возможность для введения в комплекс сравнения
так называемого эталонного объекта.

39.

Введение в комплекс сравнения эталонного объекта и
оценка статистического расстояния между ним и каждым
из реальных объектов позволяет дать оценку степени
приближения каждого из реальных объектов к эталону
Если статистические координаты эталонного объекта представить в виде:
С = (С1, С2, С3, …, СК), то обобщенное статистическое расстояния между
эталонным объектом и каждым реальным объектом будет представлено
в виде:
di (bi1 с1 ) (bi 2 с2 ) (bi3 с3 ) ... (bik сk )
2
2
2
2
Возникает возможность ранжировать анализируемые реальные объекты по
критерию статистического расстояния между ними и эталонным объектом:
чем ближе реальный объект к эталонному объекту, тем выше его оценка в
принятой системе оценочных координат (признаков). При этом каждому из
реальных объектов присваивается соответствующий ранг (от 1 до n) в
зависимости от близости к эталонному объекту (табл. ***).

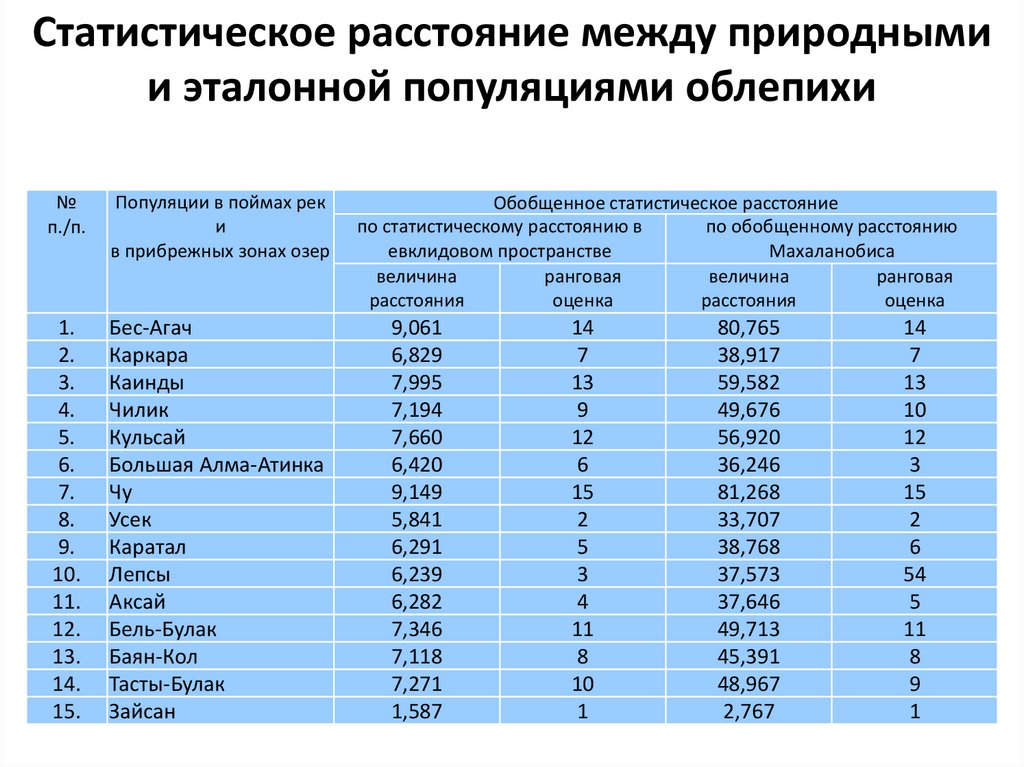
40.

Статистическое расстояние между природными
и эталонной популяциями облепихи
№
п./п.
Популяции в поймах рек
и
в прибрежных зонах озер
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
Бес-Агач
Каркара
Каинды
Чилик
Кульсай
Большая Алма-Атинка
Чу
Усек
Каратал
Лепсы
Аксай
Бель-Булак
Баян-Кол
Тасты-Булак
Зайсан
Обобщенное статистическое расстояние
по статистическому расстоянию в
по обобщенному расстоянию
евклидовом пространстве
Махаланобиса
величина
ранговая
величина
ранговая
расстояния
оценка
расстояния
оценка
9,061
6,829
7,995
7,194
7,660
6,420
9,149
5,841
6,291
6,239
6,282
7,346
7,118
7,271
1,587
14
7
13
9
12
6
15
2
5
3
4
11
8
10
1
80,765
38,917
59,582
49,676
56,920
36,246
81,268
33,707
38,768
37,573
37,646
49,713
45,391
48,967
2,767
14
7
13
10
12
3
15
2
6
54
5
11
8
9
1

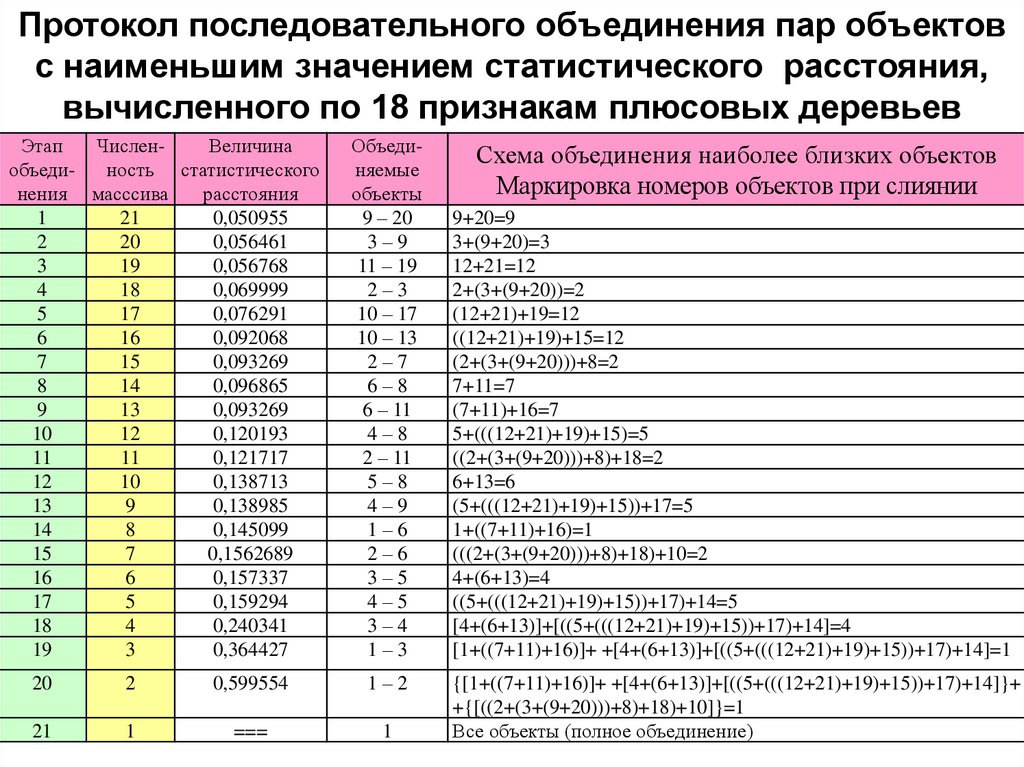
41.

Протокол последовательного объединения пар объектов
с наименьшим значением статистического расстояния,
вычисленного по 18 признакам плюсовых деревьев
Этап
ЧисленВеличина
объединость статистического
нения масссива
расстояния
1
21
0,050955
2
20
0,056461
3
19
0,056768
4
18
0,069999
5
17
0,076291
6
16
0,092068
7
15
0,093269
8
14
0,096865
9
13
0,093269
10
12
0,120193
11
11
0,121717
12
10
0,138713
13
9
0,138985
14
8
0,145099
15
7
0,1562689
16
6
0,157337
17
5
0,159294
18
4
0,240341
19
3
0,364427
Объединяемые
объекты
9 – 20
3–9
11 – 19
2–3
10 – 17
10 – 13
2–7
6–8
6 – 11
4–8
2 – 11
5–8
4–9
1–6
2–6
3–5
4–5
3–4
1–3
20
2
0,599554
1–2
21
1
===
1
Схема объединения наиболее близких объектов
Маркировка номеров объектов при слиянии
9+20=9
3+(9+20)=3
12+21=12
2+(3+(9+20))=2
(12+21)+19=12
((12+21)+19)+15=12
(2+(3+(9+20)))+8=2
7+11=7
(7+11)+16=7
5+(((12+21)+19)+15)=5
((2+(3+(9+20)))+8)+18=2
6+13=6
(5+(((12+21)+19)+15))+17=5
1+((7+11)+16)=1
(((2+(3+(9+20)))+8)+18)+10=2
4+(6+13)=4
((5+(((12+21)+19)+15))+17)+14=5
[4+(6+13)]+[((5+(((12+21)+19)+15))+17)+14]=4
[1+((7+11)+16)]+ +[4+(6+13)]+[((5+(((12+21)+19)+15))+17)+14]=1
{[1+((7+11)+16)]+ +[4+(6+13)]+[((5+(((12+21)+19)+15))+17)+14]}+
+{[((2+(3+(9+20)))+8)+18)+10]}=1
Все объекты (полное объединение)

42.

Дерево № 1
Дерево № 11
Дерево № 7
Дерево № 16
Дерево № 4
Дерево № 13
Дерево № 6
Дерево № 14
Дерево № 17
Дерево № 5
Дерево № 15
Дерево № 19
Дерево № 21
Дерево № 12
Дерево № 10
Дерево № 18
Дерево № 8
Дерево № 2
Дерево № 3
Дерево № 20
Дерево № 9
Расстояние
0,6
0,5
0,4
0,3
0,2
0,1
0,0
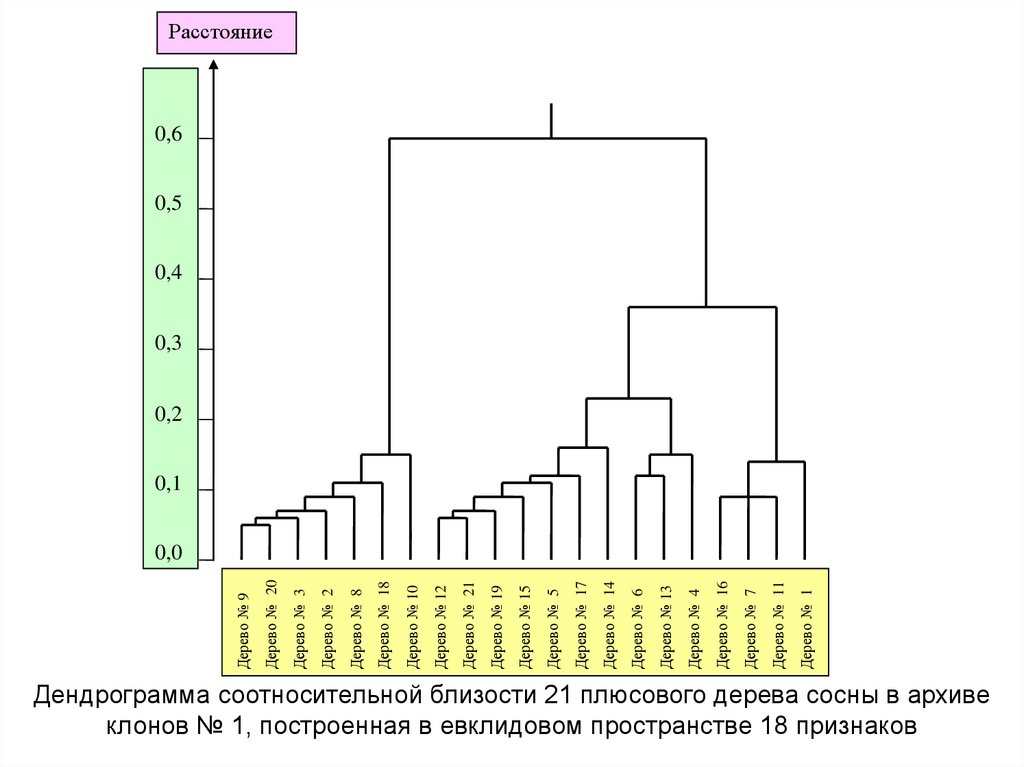
Дендрограмма соотносительной близости 21 плюсового дерева сосны в архиве
клонов № 1, построенная в евклидовом пространстве 18 признаков

43.

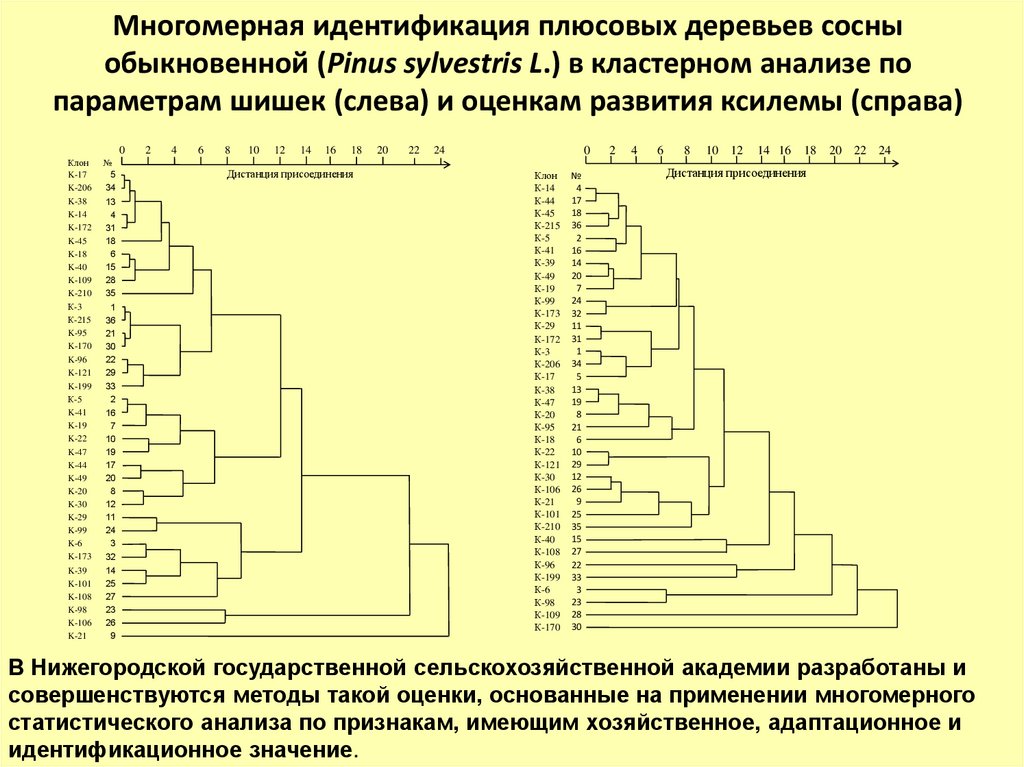
Многомерная идентификация плюсовых деревьев сосны
обыкновенной (Pinus sylvestris L.) в кластерном анализе по
параметрам шишек (слева) и оценкам развития ксилемы (справа)
0
Клон
K-17
K-206
№
5
34
K-38
K-14
K-172
K-45
K-18
K-40
K-109
K-210
13
4
31
18
6
15
28
35
К-3
К-215
K-95
K-170
K-96
K-121
1
36
21
30
22
29
K-199
К-5
K-41
K-19
K-22
K-47
K-44
K-49
K-20
K-30
K-29
K-99
K-6
K-173
33
2
16
7
10
19
17
20
8
12
11
24
3
32
K-39
K-101
K-108
K-98
K-106
K-21
14
25
27
23
26
9
2
4
6
8
10
12
14
16
18
Дистанция присоединения
20
22
0
24
Клон
К-14
К-44
К-45
К-215
К-5
К-41
К-39
К-49
К-19
К-99
К-173
К-29
К-172
К-3
К-206
К-17
К-38
К-47
К-20
К-95
К-18
К-22
К-121
К-30
К-106
К-21
К-101
К-210
К-40
К-108
К-96
К-199
К-6
К-98
К-109
К-170
№
4
17
18
36
2
16
14
20
7
24
32
11
31
1
34
5
13
19
8
21
6
10
29
12
26
9
25
35
15
27
22
33
3
23
28
30
2
4
6
8
10 12
14 16
18
20 22 24
Дистанция присоединения
В Нижегородской государственной сельскохозяйственной академии разработаны и
совершенствуются методы такой оценки, основанные на применении многомерного
статистического анализа по признакам, имеющим хозяйственное, адаптационное и
идентификационное значение.

44.

5. Реализация метода
в электронных таблицах
(Excel, SPSS, STATISTICA)

45.

люсовые деревья, имеющие наиболее высоки
начения генетической индивидуальности,
азмножаются прививкой

46.

Выращивание посадочного материала, получаемого
на лесосеменных плантациях, происходит в теплица
использованием контейнерных технологий

47.

ля выращивания сеянцев из селекционных семян
спользуют контейнерные технологии
нтейнерные технологии успешно реализованы в ГБУ НО «Семеновски
ецсемлесхоз», на базе которого открыт филиал кафедры «Лесные

48.

Для удобства заготовки шишек необходимым мероприятием
является формирование кроны

49.

Спасибо
за внимание