Методы экспериментальных исследований

1.

Методы экспериментальных
исследований
Наблюдение – это систематическое,
целенаправленное восприятие того или иного объекта
или явления без воздействия на него. Наблюдение
позволяет получить первоначальную информацию об
изучаемом объекте или явлении.
Эксперимент – метод изучения объекта (явления),
когда исследователь активно и целенаправленно
воздействует на него путем создания искусственных
условий или использует естественные условия,
необходимые для выявления некоторых свойств
данного объекта (явления).

2.

Измерение экспериментальных
данных
Измерение – процесс нахождения значения
физической величины с помощью специальных
технических средств – измерительных приборов.
Измерить какую-либо физическую величину значит
сравнить ее с другой однородной ей физической
величиной, принятой за единицу меры.
При измерении физических величин пользуются не
эталонами,
которые
хранятся
в
специальных
государственных метрологических учреждениях, а
измерительными приборами, которые тем или иным
способом сверены с эталонами.

3.

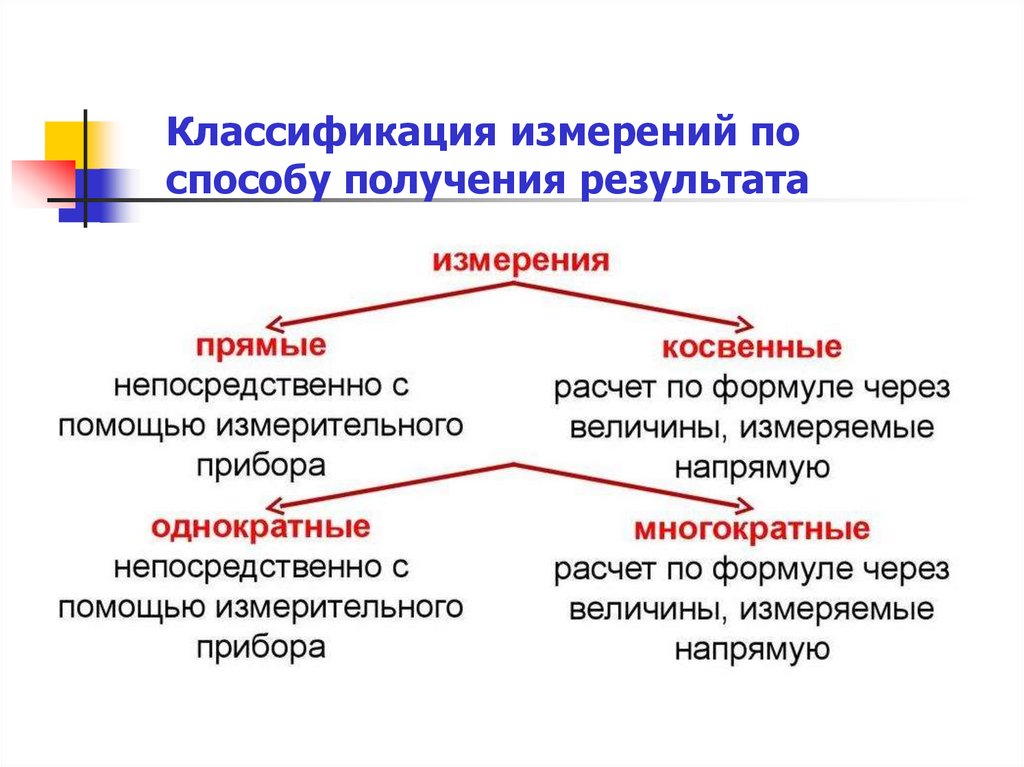
Классификация измерений по
способу получения результата

4.

Точность измерения
Опыт показывает, что вследствие неточности
измерительных приборов, несовершенства наших органов
чувств, неполноты наших знаний, трудности учета всех
побочных явлений, при многократном повторении одного
и того же измерения получаются разные числовые
значения изучаемой физической величины.
При практическом использовании результатов тех или
иных измерений возникает вопрос об истинном значении
изучаемой физической величины, о точности
измерения.

5.

Точность измерений.
Воспроизводимость результатов
Точность измерений – характеристика качества
измерений, отражающая близость результатов измерений
к истинному значению измеряемой величины.
Воспроизводимость результатов – возможность
повторить измерение через любой промежуток времени с
получением результатов, разброс значений которых не
превышает требований к точности измеряемой величины.

6.

Погрешность измерений
Для количественной оценки используется
понятие «погрешность (ошибка)
измерений».
Чем меньше погрешность, тем выше
точность.
Оценка погрешности измерений – одно
из важных мероприятий по обеспечению
достоверности измерений.

7.

Абсолютная погрешность
Абсолютная погрешность измерения – разность
между результатом измерения и действительным
(истинным) значением физической величины:
- действительное значение определяется с
помощью эталонного прибора или воспроизводится
эталонной мерой.

8.

Относительная погрешность
Относительная погрешность измерения - это
отношение
абсолютной
погрешности
к
тому
значению, которое принимается за истинное (часто
выраженное в процентах):
- действительное или измеренное значение
величины.

9.

Классификация погрешностей

10.

Случайные погрешности (ошибки)
Случайные погрешности (ошибки) – это погрешности,
изменяющие свою величину или знак от опыта к опыту, при
измерениях, выполненных одинаковым образом и при
одинаковых условиях.
Случайные погрешности обуславливаются большим
числом случайных причин (вибрации отдельных частей
прибора, различные изменения в среде, трение и др.),
действующих в каждом отдельном измерении различным,
неизвестным образом. других причин, которые практически
невозможно исключить.
Предсказать величину случайной погрешности для
одного измерения в принципе невозможно!

11.

Случайные погрешности
Влияние случайных погрешностей – выражается в
разбросе полученных результатов относительно
математического ожидания, поэтому количественно
наличие случайных погрешностей оценивается
среднеквадратичным отклонением (СКО).
Причины появления их носят случайный характер,
они могут быть оценены методами математической
статистики.

12.

Прямые многократные измерения
Проведем прямые многократные измерения одной и той же
физической величины x.
Если измеряемая величина x непрерывна, то в результате
достаточно большого числа n измерений получим ряд
значений
x1, x2,…, xn.
Результаты можно представить графически.
Для этого область, в которой расположены все полученные
значения, разделим на некоторое количество интервалов
одинаковой ширины Δx и подсчитаем количество
измерений, попавших в каждый из этих интервалов.

13.

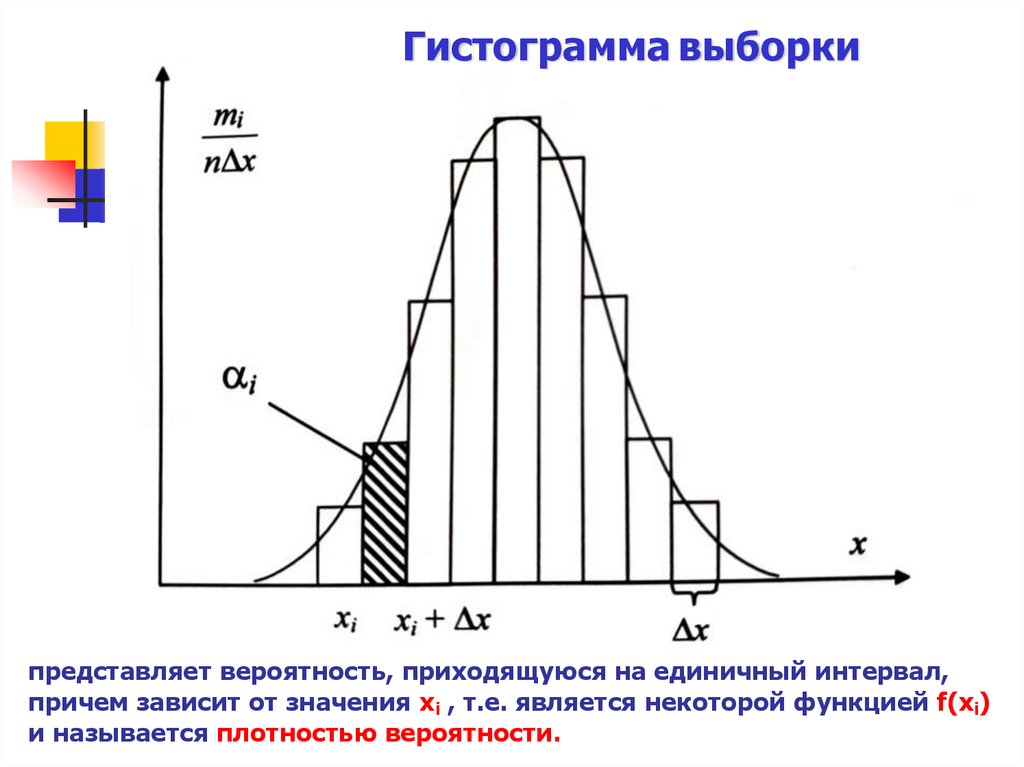
Гистограмма выборки
представляет вероятность, приходящуюся на единичный интервал,
причем зависит от значения xi , т.е. является некоторой функцией f(xi)
и называется плотностью вероятности.

14.

При большом количестве измерений относительную
частоту того, что величина x может принимать
значения в интервале от xi до (xi+Δ), называют
вероятностью
lim
n
mi
n x
i
n
i
представляет вероятность, приходящуюся на
единичный интервал, причем зависит от значения
xi , т.е. является некоторой функцией f(xi) и
называется плотностью вероятности.
f x dx 1
m
Вероятность того, что измеряемая
случайная величина принимает какоелибо значение в интервале от –∞ до
∞, равна 1, следовательно площадь
под кривой распределения f(x) равна 1.

15.

Нормальное распределение (Гаусса)
случайных величин
1
f ( x)
e
2
( x )2
2 2
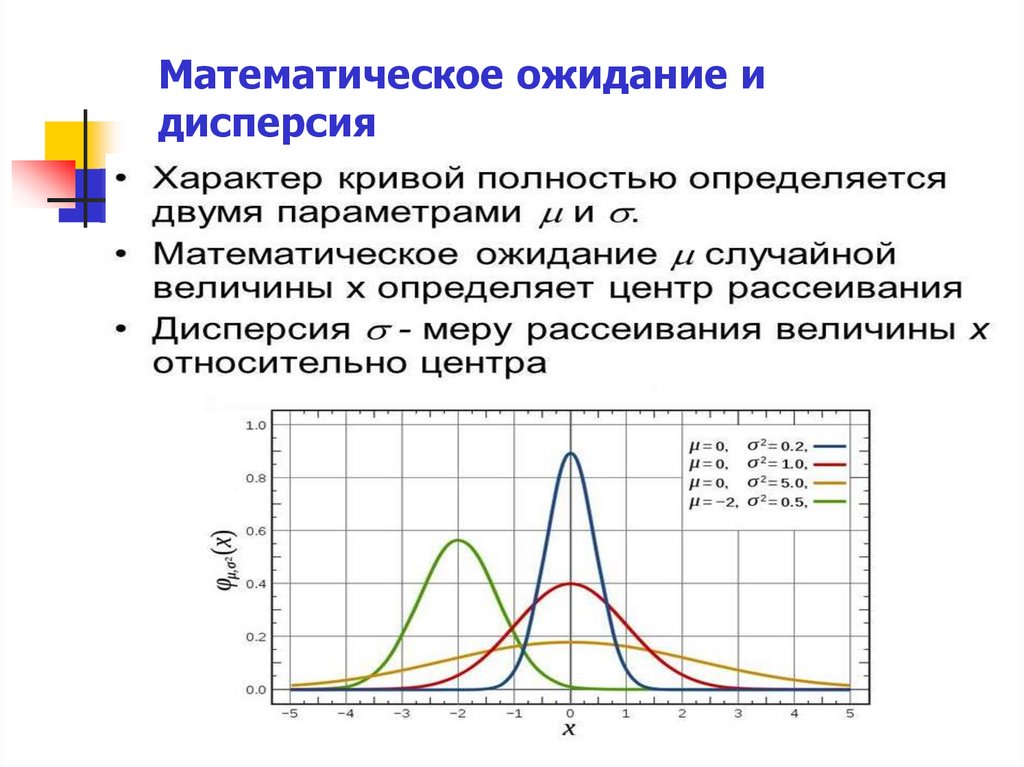
µ - математическое ожидание, можно охарактеризовать как
среднее арифметическое значений измеряемой величины,
полученное при бесконечном числе испытаний (может
обозначаться как m);
σ - дисперсия, характеризует размах вариации, то есть
ширину распределения данных (может обозначаться как S);
переменная x, для которой рассчитывается значение
функции f(x), т.е. плотность вероятности.

16.

Математическое ожидание и
дисперсия

17.

Математическое ожидание – показывает
среднее ожидаемое значение и рассчитывается по
формуле (среднее значение случайной величины)
n
1
xi
n i 1
СКО – показывает насколько в среднем большинство
значений отклонится от математического ожидания
n
1
2
( xi x )
n 1 i 1

18.

Доверительный интервал
Истинное значение измеренной величины x лежит в
интервале от (x - x) до (x + x),
где x называется доверительным интервалом.
Вероятность
этого
события
(доверительная
вероятность) составляет P.
Доверительный интервал рассчитывается по
формуле
x t P , n 1
x
n
где tP,n-1 - коэффициент Стьюдента, зависящий от
доверительной вероятности P и числа измерений n
(находим в приложении).

19.

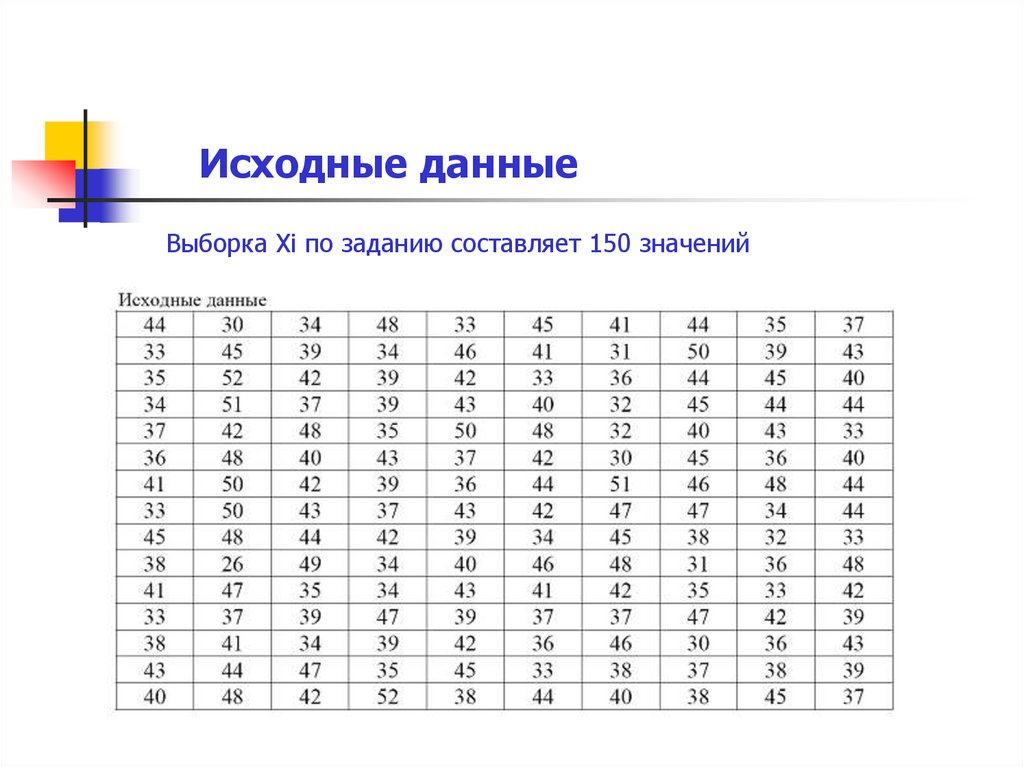
Исходные данные
Выборка Xi по заданию составляет 150 значений

20.

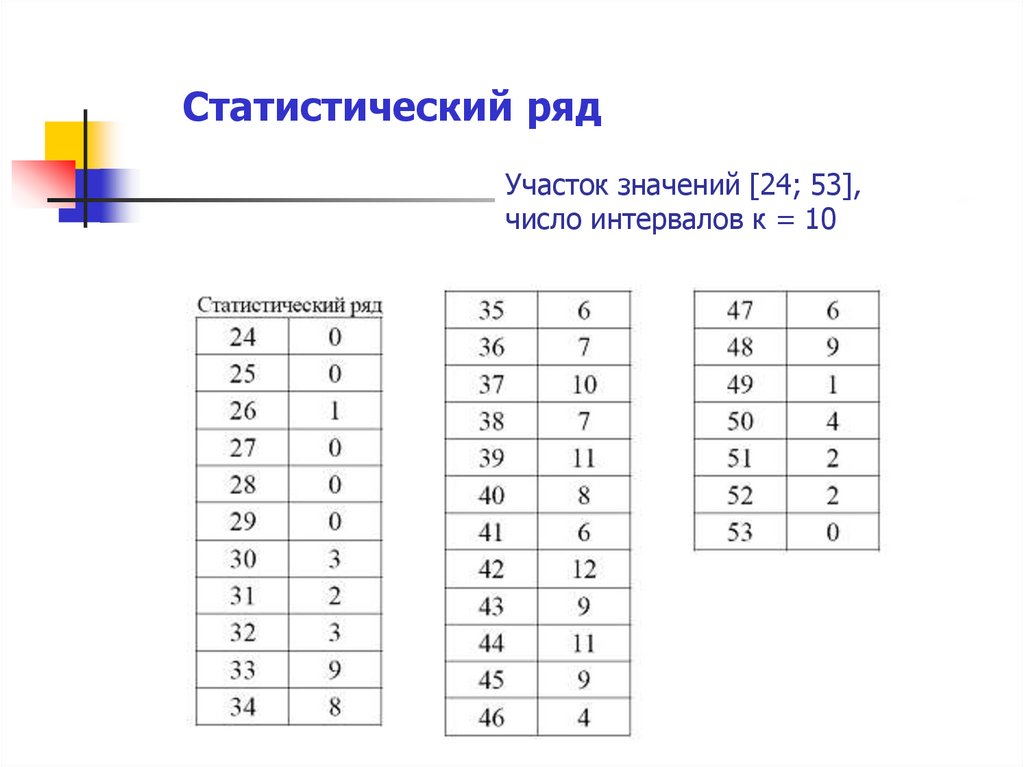
Статистический ряд
Участок значений [24; 53],
число интервалов к = 10

21.

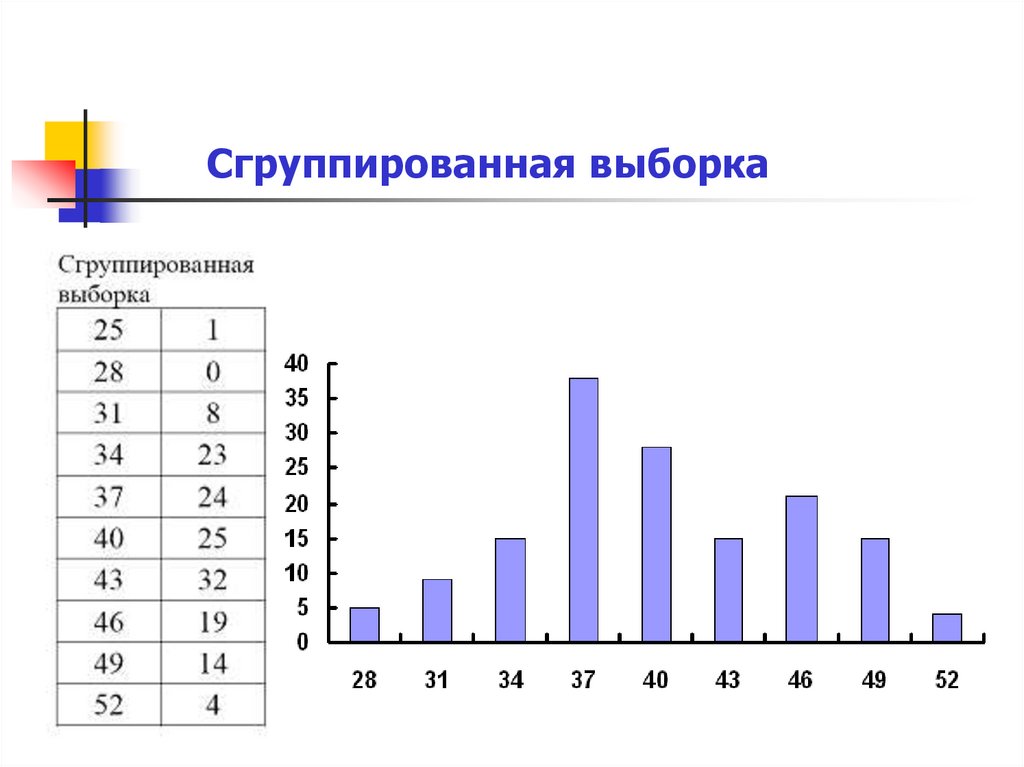
Сгруппированная выборка

22.

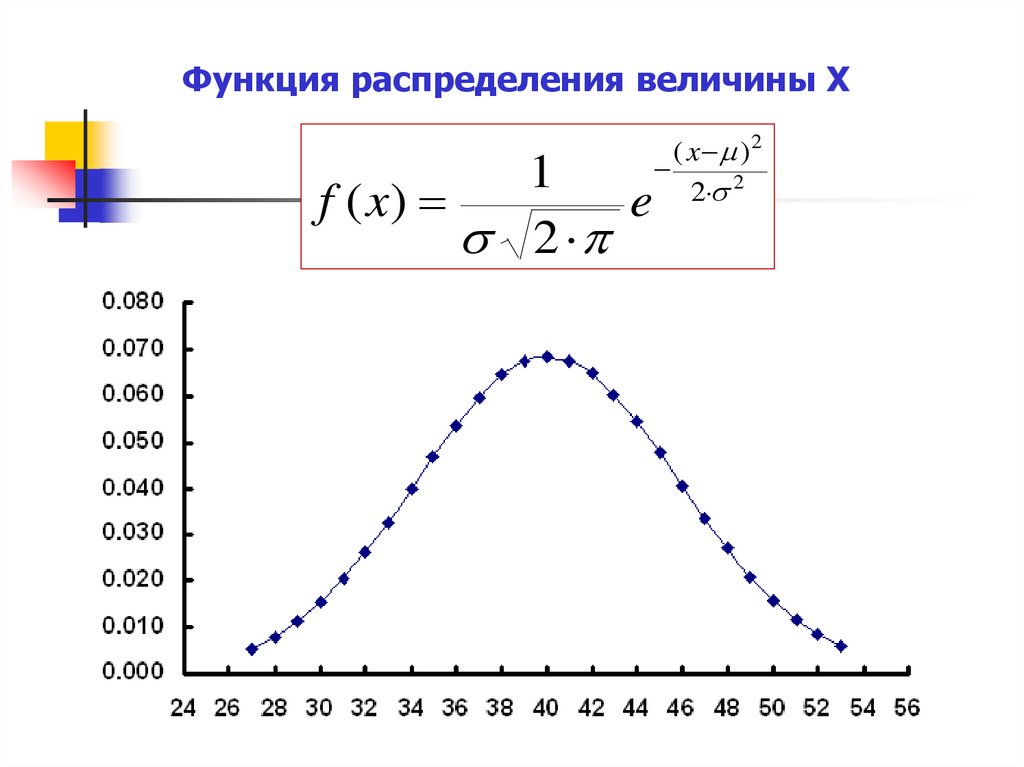
Функция распределения величины Х
1
f ( x)
e
2
( x )2
2 2

23.

Алгоритм оценки измеряемой величины
Среднее арифметическое
величины (n=150)
1.
2.
x
3.
4.
x
значений
измеряемой
Среднее квадратическое отклонение
1 n
2
( xi x ) (для 150 значений)
n 1 i 1
x t P , n 1
Доверительный интервал
n
x x x
Запись результата измерений согласно
правилам округления

24.

Правила округления
1. Точность результатов измерений и точность вычислений при
обработке результатов измерений должны быть согласованы с требуемой
точностью получаемой оценки измеряемой величины.
2. Погрешность оценки измеряемой величины следует выражать не
более чем двумя значащими цифрами.
Две значащие цифры в погрешности оценки измеряемой величины
сохраняют:
- при точных измерениях;
- если первая значащая цифра не более трех.
3. Сохраняемую значащую цифру в погрешности оценки измеряемой
величины при округлении увеличивают на единицу, если отбрасываемая
цифра неуказываемого младшего разряда больше либо равна пяти, и не
изменяют, если она меньше пяти.