Похожие презентации:
Методы и средства исследования и оптимизации процессов. Основные понятия
1.
Методы и средстваисследования и
оптимизации процессов .
Основные понятия.
Фролова Мария Сагитовна
marsag@list.ru
2.
Оптимизируются те или иные объекты. Дляоптимизации объекта следует иметь об этом объекте
достаточное количество априорной информации.
Априорная информация – уровень достоверной
информации об объекте исследования, позволяющей
построить модель того или иного уровня
детализации и достоверности.
3.
При исследовании объекта применяютаналитические методы, т. е. методы,
основанные
на
применении
математики, физики, теоретической
механики, химии и др. наук. Задачей
аналитических
методов
является
получение той или иной теоретической
(математической) модели объекта.
По
определению
Е.А.
Козловского
«Математическая модель процесса бурения
представляет собой динамическую аналогию
данного объекта с нетождественным подобием
свойств».
4.
Таким образом,модель
процесса
бурения
–
воспроизведенный в той или
иной степени охвата по
объему
и
детализации
влияющих факторов процесс
формирования
ствола
скважины.
Результаты исследования могут быть представлены в
виде
таблиц,
график
и
уравнений,
т.е.
математическое
описание
технологического
процесса.
5.
Сущность математического описания объекта(системы) или процесса заключается в получении
математической
модели
или
соотношения,
связывающего характеристики входящего в объект
материала и выходящего продукта:
Y = F{X},
где Y – сов-ть выходных параметров процесса,
которые определяют свойства выходящего продукта.
Х – совокупность выходных параметров (факторов),
определяющих характеристики процесса (объекта) и
свойства входящего материала (продукта).
F{X} – символ, называемый оператором, который
характеризует математическую модель объекта или
системы.
6.
Основной характеристикой объекта исследованийявляется его сложность. Она определяется
количеством разнообразия, или числом различимых
состояний, в каждом из которых может находиться
объект. В этом случае можно говорить о простых
объектах, сложных объектах и системах объектов.
Простой объект – это такой объект, в котором
изменение влияющих факторов приводит к
предсказуемому изменению выходных данных. Как
правило, подобное может происходить только на
определенном ограниченном интервале изменения
влияющих факторов.
7.
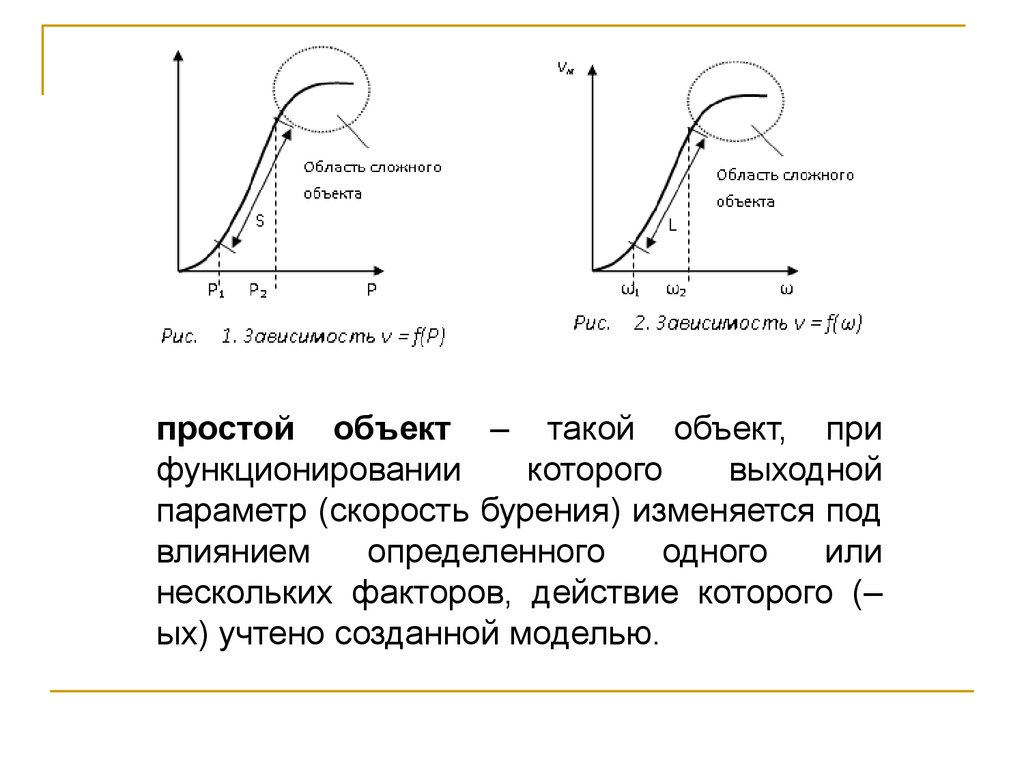
простой объект – такой объект, прифункционировании
которого
выходной
параметр (скорость бурения) изменяется под
влиянием
определенного
одного
или
нескольких факторов, действие которого (–
ых) учтено созданной моделью.
8.
Сложный объект – это объект, при функционировании которогопод влиянием факторов происходит изменение неучтенных
параметров, которые, в свою очередь, оказывают влияние на
выходной параметр. Иначе говоря, сложный объект – это объект,
действие которого неадекватно созданной для оценки объекта
модели.
Система объектов может включать несколько отдельных
«блоков», каждый из которых является сложным объектом.
Пример. Работа бурового агрегата, как система объектов,
включает:
– работу бурового инструмента, осуществляющего углубку забоя;
– работу бурильной колонны, передающей буровому
инструменту
крутящий момент, осевую нагрузку и промывочную жидкость;
– работу бурового станка;
– работу бурового насоса.
9.
Как проверить истинность суждений о свойствахокружающего мира?
Данные – результаты некоторого количества
измерений какой-либо ПЕРЕМЕННОЙ (переменных) –
variable. Например:
- вес, длина тела, пол, окрас, температура .....
Статистика – инструмент для количественного анализа
и интерпретации данных
10.
11.
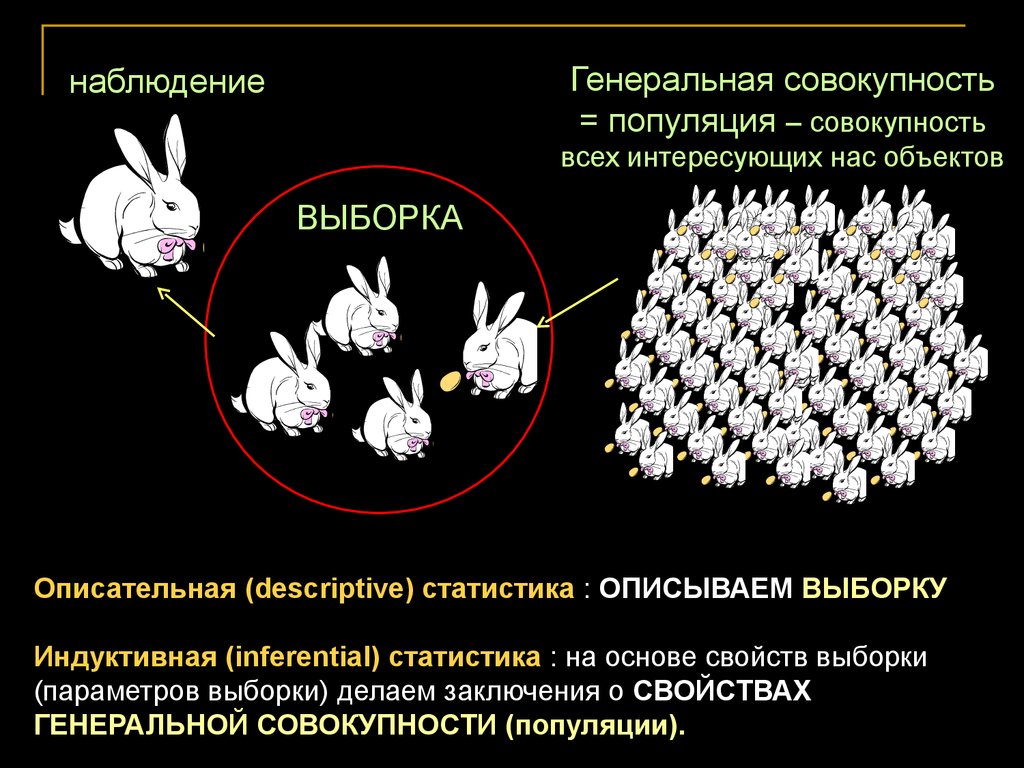
Генеральная совокупность= популяция – совокупность
наблюдение
всех интересующих нас объектов
ВЫБОРКА
Описательная (descriptive) статистика : ОПИСЫВАЕМ ВЫБОРКУ
Индуктивная (inferential) статистика : на основе свойств выборки
(параметров выборки) делаем заключения о СВОЙСТВАХ
ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ (популяции).
12.
Выборка должна быть репрезентативной, т.е. её свойствадолжны ОТРАЖАТЬ СВОЙСТВА ПОПУЛЯЦИИ.
Для этого она должна быть СЛУЧАЙНОЙ (random) – т.е.,
все особи в популяции должны иметь одинаковые шансы
попасть в неё, и попадание в выборку одного элемента не
должно влиять на попадание другого элемента.
клетка
Dr. Nostat сформировал выборки для эксперимента; в одну
поместил зверьков, которые первыми вышли из клетки, а в другую
– тех, кто в ней остался
13.
Три основные концепции в анализе данных:1. Что такое РАСПРЕДЕЛЕНИЕ ПЕРЕМЕННОЙ и как
его описывать
2. Что такое распределение ВЫБОРОЧНЫХ СРЕДНИХ
и как оно связано с распределением переменной
3. Что такое СТАТИСТИКА КРИТЕРИЯ
Необходимо для обдумывания и обсуждения данных
14.
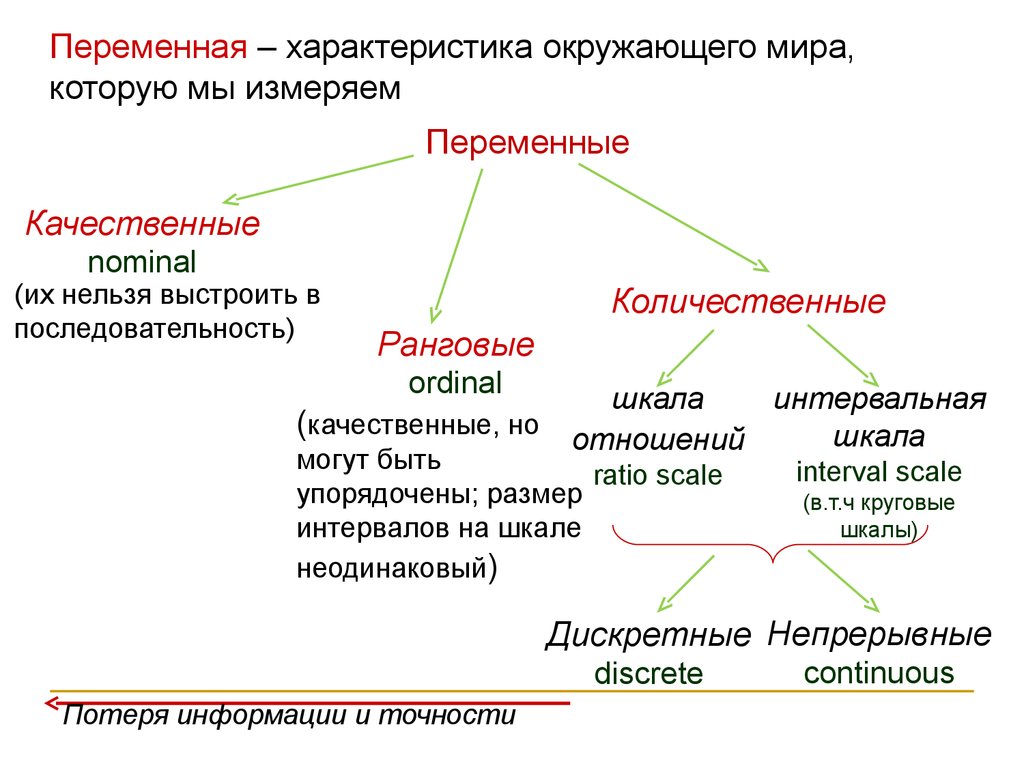
Переменная – характеристика окружающего мира,которую мы измеряем
Переменные
Качественные
nominal
(их нельзя выстроить в
последовательность)
Количественные
Ранговые
ordinal
(качественные, но
шкала
интервальная
шкала
отношений
могут быть
ratio scale
упорядочены; размер
интервалов на шкале
неодинаковый)
interval scale
(в.т.ч круговые
шкалы)
Дискретные Непрерывные
discrete
Потеря информации и точности
continuous
15.
шкала отношений (ratio scale):•размер интервалов на протяжении всей шкалы
одинаковый;
•существует реальное нулевое значение.
Примеры: масса тела, размер выводка, объём,
температура по Кельвину
интервальная шкала (interval scale):
•размер интервалов на протяжении всей шкалы
одинаковый;
•положение нулевой точки выбрано произвольно.
Примеры: температура по Цельсию, время дня, дата
16.
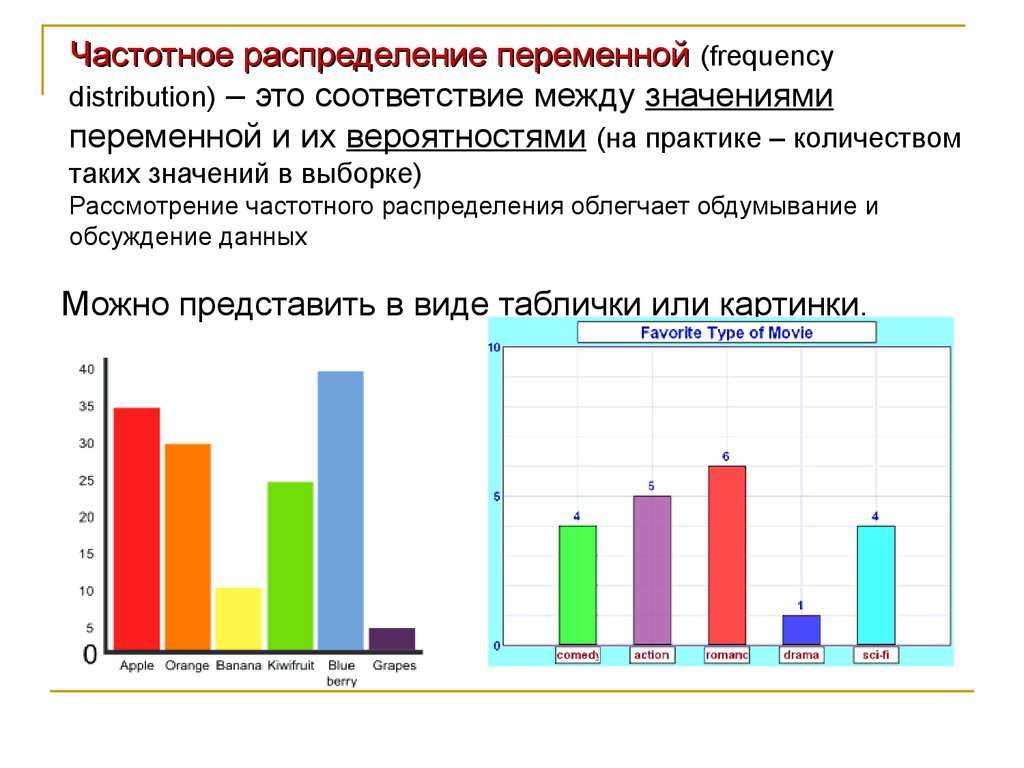
Частотное распределение переменной (frequencydistribution) – это соответствие между значениями
переменной и их вероятностями (на практике – количеством
таких значений в выборке)
Рассмотрение частотного распределения облегчает обдумывание и
обсуждение данных
Можно представить в виде таблички или картинки.
17.
Частотное распределение переменной (frequency distribution)Картинка распределения КАЧЕСТВЕННЫХ или ранговых переменных
(bar graph). Столбчатая диаграмма («гистограмма» - не совсем верно).
трава
промежутки между
столбиками
корни плоды
Виды пищи
Оставим на некоторое время качественные и ранговые
переменные и обратимся только к КОЛИЧЕСТВЕННЫМ
листва
18.
Частотное распределение количественной переменнойВзвешиваем N кроликов
19.
Частотное распределение количественной переменной1. Упорядочим по возрастанию значения переменной
(выстроим кроликов от меньшего к большему);
2. разобьём их на группы по равным интервалам.
20.
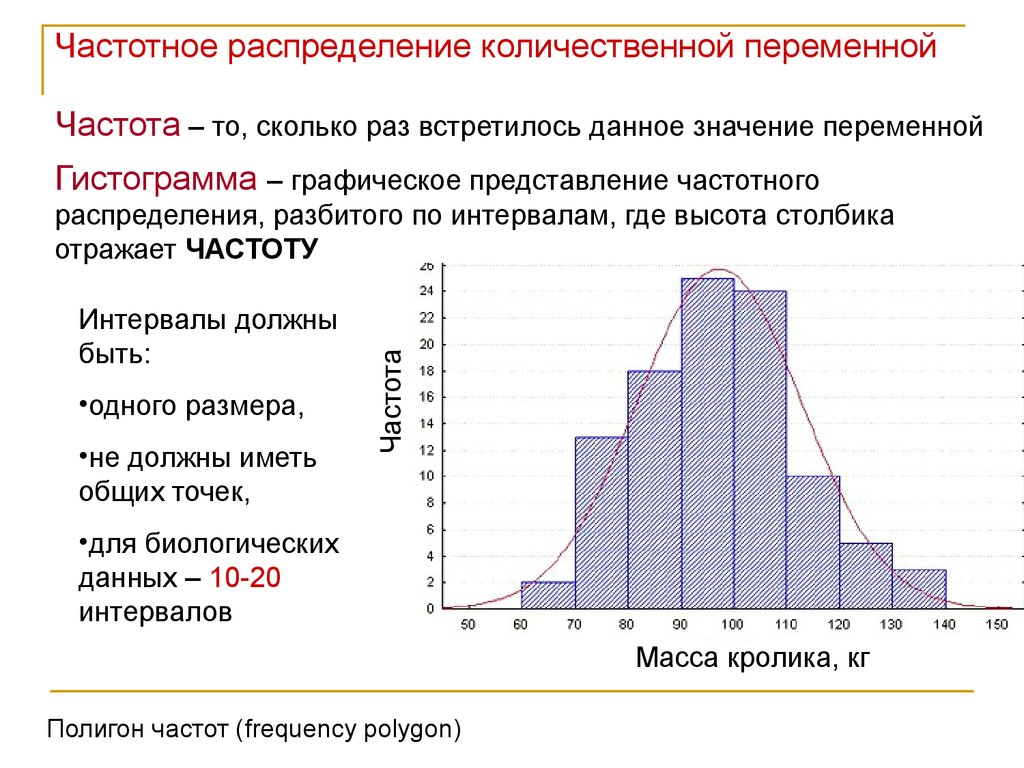
Частотное распределение количественной переменнойЧастота – то, сколько раз встретилось данное значение переменной
Гистограмма – графическое представление частотного
Интервалы должны
быть:
•одного размера,
•не должны иметь
общих точек,
Частота
распределения, разбитого по интервалам, где высота столбика
отражает ЧАСТОТУ
•для биологических
данных – 10-20
интервалов
Масса кролика, кг
Полигон частот (frequency polygon)
21.
Частотное распределение переменной22.
Как описать частотное распределение переменной?Три ОСНОВНЫЕ ХАРАКТЕРИСТИКИ, которыми можно почти
полностью описать большинство распределений
1. «Середина» распределения;
2. «Ширина» распределения;
3. Форма распределения
Речь идёт не только о количественных данных, но и о
качественных
23.
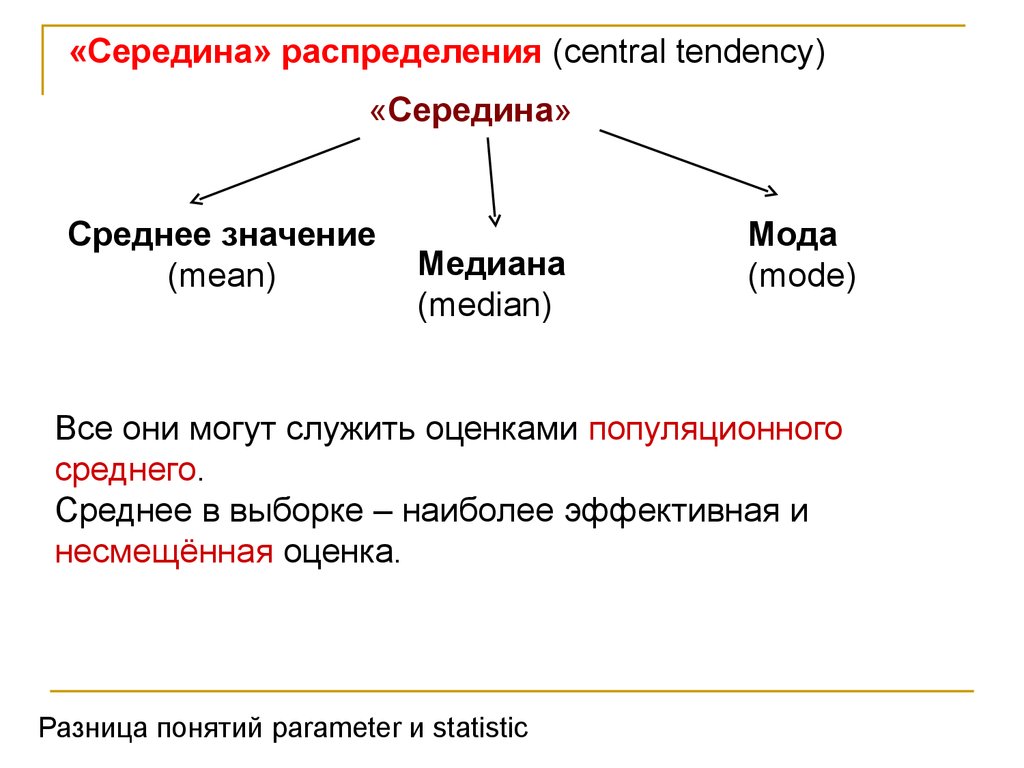
«Середина» распределения (central tendency)«Середина»
Среднее значение
(mean)
Медиана
(median)
Мода
(mode)
Все они могут служить оценками популяционного
среднего.
Среднее в выборке – наиболее эффективная и
несмещённая оценка.
Разница понятий parameter и statistic
24.
Частотное распределение переменной«Середина» распределения
Среднее значение – сумма всех значений переменной,
делённая на количество значений
*«balancing point» method
Среднее для выборки
X
X
i
n
i
Среднее для популяции
X
N
25.
Частотное распределение переменной«Середина» распределения
Медиана (median)– значение, которое делит
распределение пополам (его площадь в т.ч.): половина
значений больше медианы, половина – не больше.
1,0 1,5 3,2 4,1
5,7
6,0
7,1
7,9
9,5
10,4
11,0
Медиана
Имеет смысл не только для количественных переменных,
но и для ранговых! (не для качественных).
26.
Частотное распределение переменнойЕсли распределение не симметричное, медиана
лучше характеризует центр распределения.
она содержит меньше информации, чем среднее
(определяется только рангом измерений, а не их значениями)
но зато она не чувствительна к «аутлаерам» и может
применяться даже в случае, если не для всех особей
измерения точные.
Распределение можно поделить не только на ДВЕ
равные части, но и на:
четыре (значения, стоящие на границах - квартили);
восемь (... октили);
сто (... процентили);
N (... квантили).
27.
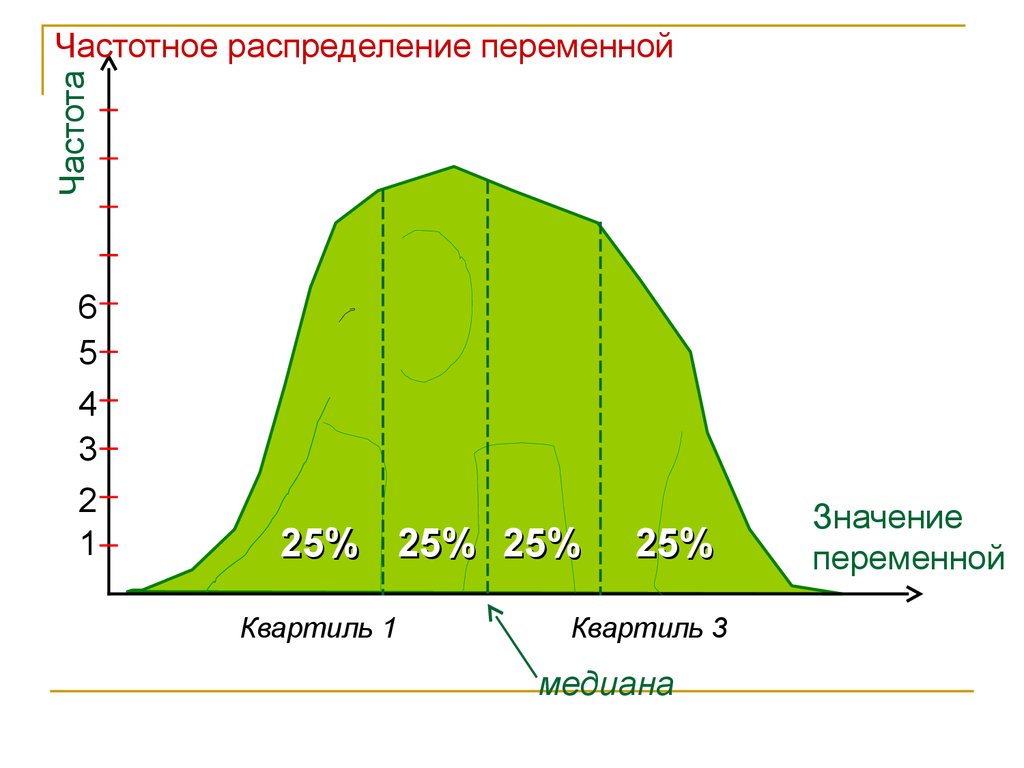
Частотное распределение переменнойКвартили (quartiles) делят распределение на
четыре части так, что в каждой из них оказывается
поровну значений (2-я квартиль = медиана).
1-я квартиль = 25% процентиль
3-я квартиль = 75% процентиль
Интерквартильный размах – разница между
третьей и первой квартилями.
Пример про 500 р и магазин
28.
ЧастотаЧастотное распределение переменной
6
5
4
3
2
1
25% 25% 25%
Квартиль 1
25%
Квартиль 3
медиана
Значение
переменной
29.
Частотное распределение переменной«Середина» распределения
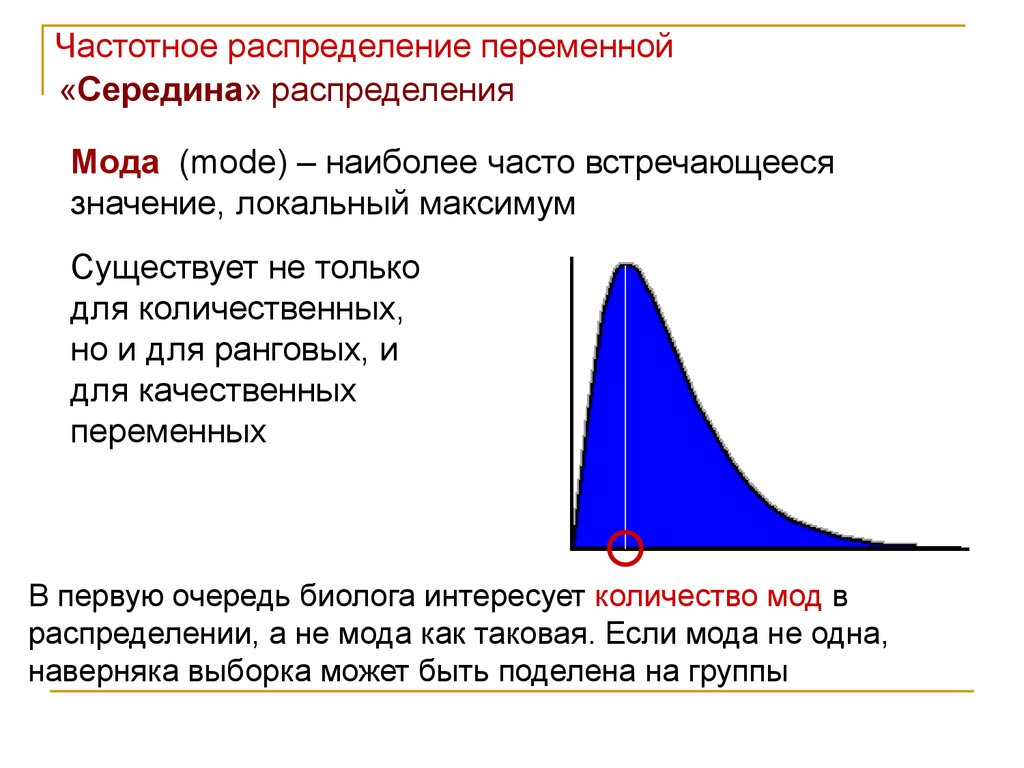
Мода (mode) – наиболее часто встречающееся
значение, локальный максимум
Существует не только
для количественных,
но и для ранговых, и
для качественных
переменных
В первую очередь биолога интересует количество мод в
распределении, а не мода как таковая. Если мода не одна,
наверняка выборка может быть поделена на группы
30.
Частотное распределение переменной«Середина» распределения
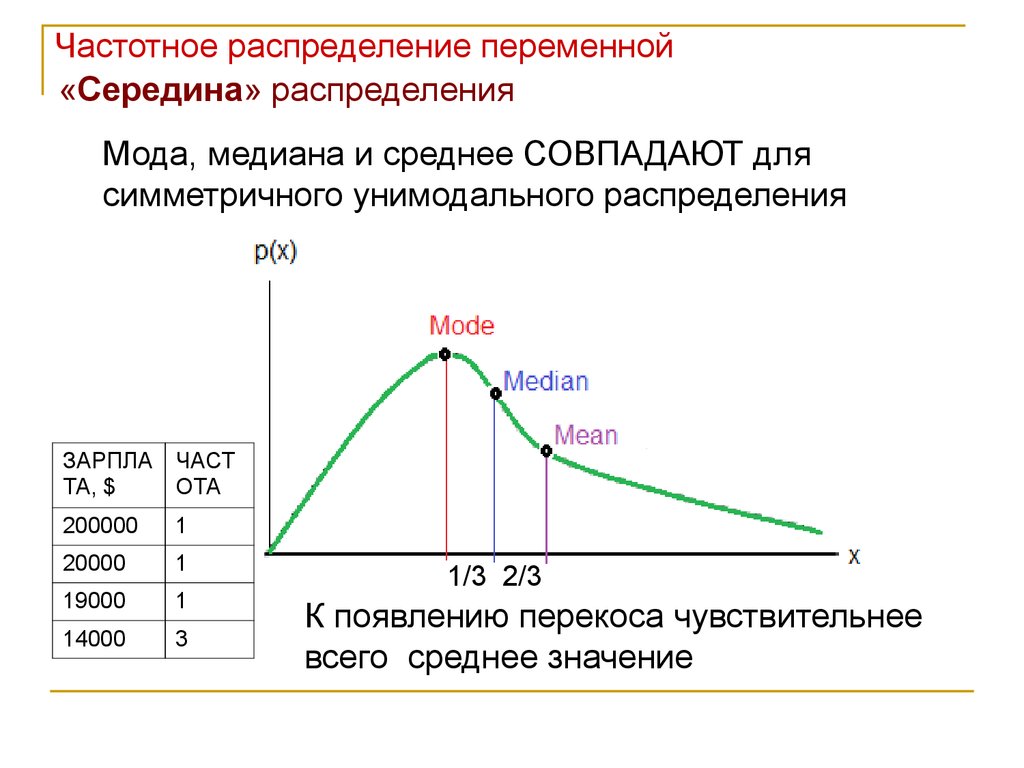
Мода, медиана и среднее СОВПАДАЮТ для
симметричного унимодального распределения
ЗАРПЛА ЧАСТ
ТА, $
ОТА
200000
1
20000
1
19000
1
14000
3
1/3 2/3
К появлению перекоса чувствительнее
всего среднее значение
31.
Для публикацийТрадиционно, для выборки приводят среднее
значение (mean) – удобно для сравнения с литературой
и пр.;
Если распределение скошенное, дополнительно
приводят медиану (М);
Моду не приводят, иногда бывает важно упомянуть,
сколько в распределении мод.
32.
Частотное распределение переменной«Ширина» распределения = Разброс*
Размах
(range)
Дисперсия
Стандартное
(variance)
отклонение
(standard deviation)
Размах (range) – разность между максимальным и
минимальным значениями = Xn – X1
Хорош тем, что легко считается и имеет «биологический
смысл».
Плох тем, что зависит лишь от 2-х точек из распределения.
Недооценивает истинный размах в популяции.
* Это лишь основные параметры разброса
33.
Частотное распределение переменнойРазброс распределения
Стандартное отклонение (standard deviation)
Для выборки:
s
(X
i
X)
i
n 1
Поправка на то, что в
выборке разброс
всегда будет меньше,
чем во всей популяции
Для популяции:
2
(x
i
)
2
i
n
Сумма квадратов
(sum of squares = SS)
Стандартное отклонение зависит ото всех значений
переменной.
Измеряется в тех же единицах, что и переменная!
34.
Частотное распределение переменнойРазброс распределения
Дисперсия (variance)
Для выборки:
s
2
2
(
X
X
)
i
i
n 1
Для популяции:
2
2
(
x
)
i
i
n
Равна стандартному отклонению в квадрате и содержит
почти ту же информацию; измеряется в единицах
переменной, возведённых в квадрат (что не всегда
удобно).
Дисперсия используется скорее в различных статистических тестах, а
не в описательной статистике
35.
Частотное распределение переменнойРазброс распределения
Коэффициент вариации
(Coefficient of variation)
s 100
CV
X
Даёт понять, насколько на самом деле велик разброс
в данных, независимо от масштаба измерений.
(маленький разброс – меньше 5%)
Не годится для данных, измеренных по интервальной
шкале (температура, время и пр.)
36.
Параметры разброса для качественных данных:Индексы разнообразия (indices of diversity)
Показывают, насколько равномерно данные распределены
по категориям. Разнообразие считается высоким, когда
распределение более-менее равномерное, и низким, когда
превалирует 1-2 категории
Индекс Шеннона-Винера
k
H pi log pi
i 1
p = доля объектов в той или иной категории;
k – число категорий.
J
H
log k
Нормированный индекс Шеннона ( 0;1 )
Этих индексов много для разных целей; это показатели
ОПИСАТЕЛЬНОЙ статистики!
37.
Для публикацийТрадиционно, вместе со средним значением
приводят стандартное отклонение (±SD);
Иногда в статье приводится размах, но в дополнение
следует привести ещё какую-нибудь характеристику
разброса.;
Коэффициент вариации приводят, если хотят
сравнить разброс в разных по характеру данных.
38.
Частотное распределение переменнойПо ФОРМЕ распределения различаются:
1. По количеству «максимумов» (мод):
мультимодальное
унимодальное
бимодальное
обычно возникают, если популяция имеет
естественные обособленные подгруппы
39.
Частотное распределение переменнойПо ФОРМЕ распределения различаются:
2. По признаку симметрии:
Симметричное
Скошенное (skewed)
влево
negatively
вправо
(positively)
40.
Частотное распределение переменнойПо ФОРМЕ распределения различаются:
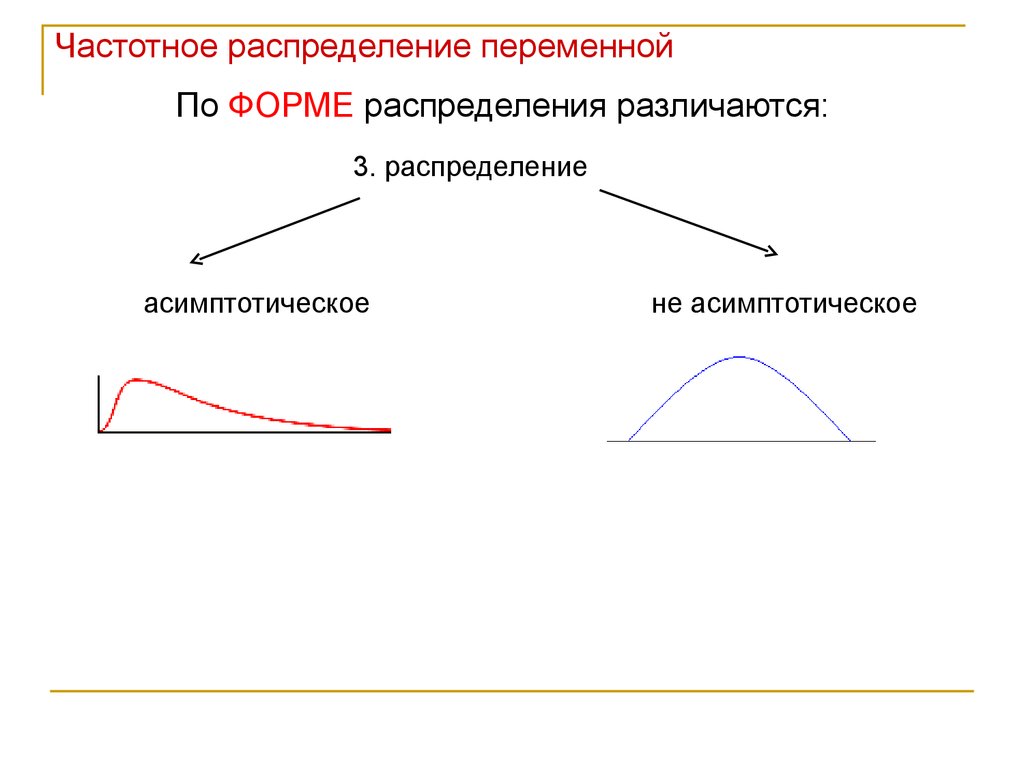
3. распределение
асимптотическое
не асимптотическое
41.
Частотное распределение переменнойНормальное распределение (Гауссово):
первое знакомство
Унимодальное
Симметричное
Асимптотическое
Это
непрерывное
распределение
Высота деревьев, масса тела новорожденных, IQ, скорость
прохождения лабиринта крысами и многие, многие другие переменные
Название в честь Гаусса не совсем справедливо – первым его описал вовсе не он.
Симметрия и эксцесс.
42.
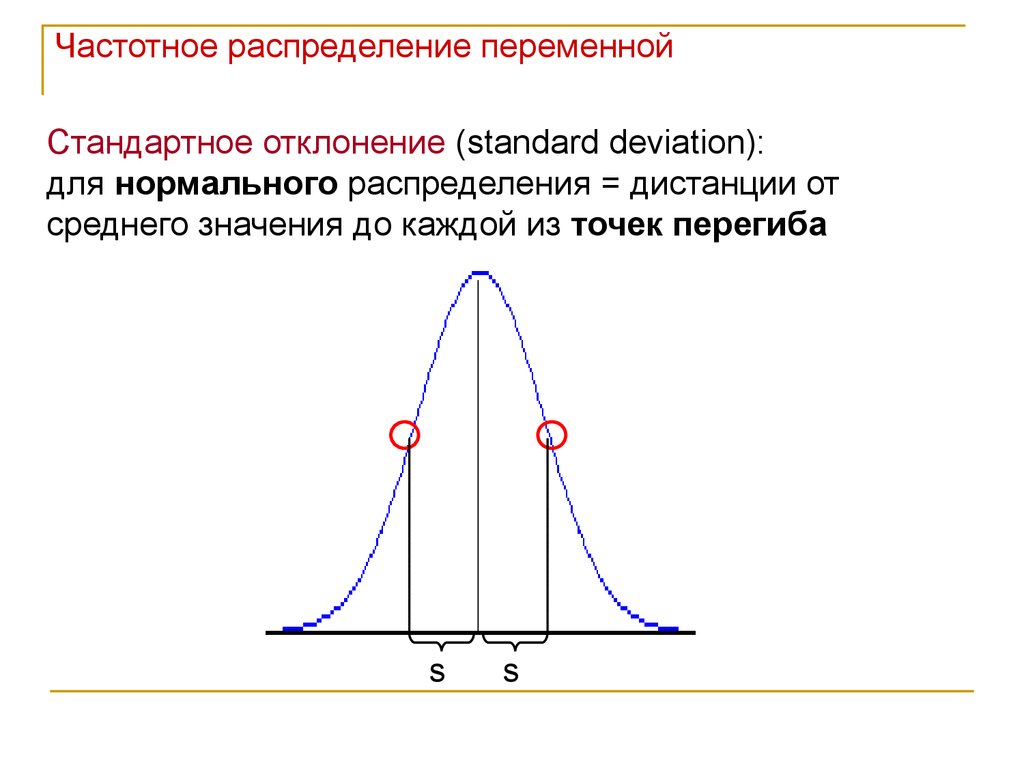
Частотное распределение переменнойСтандартное отклонение (standard deviation):
для нормального распределения = дистанции от
среднего значения до каждой из точек перегиба
s
s
43.
Частотное распределение переменной«Площадь распределения»
Площадь, которую занимает график распределения,
соответствует количеству измерений в выборке.
частота
Отрезая часть распределения на графике, мы
отделяем эквивалентную часть от выборки
16% площади
распределения ~
16% объёма
выборки
масса, кг
44.
Частотное распределение переменнойПроцентили и z-оценка (standard score)
95% процентиль – значение переменной, левее
которого находится 95% значений переменной
95%
45.
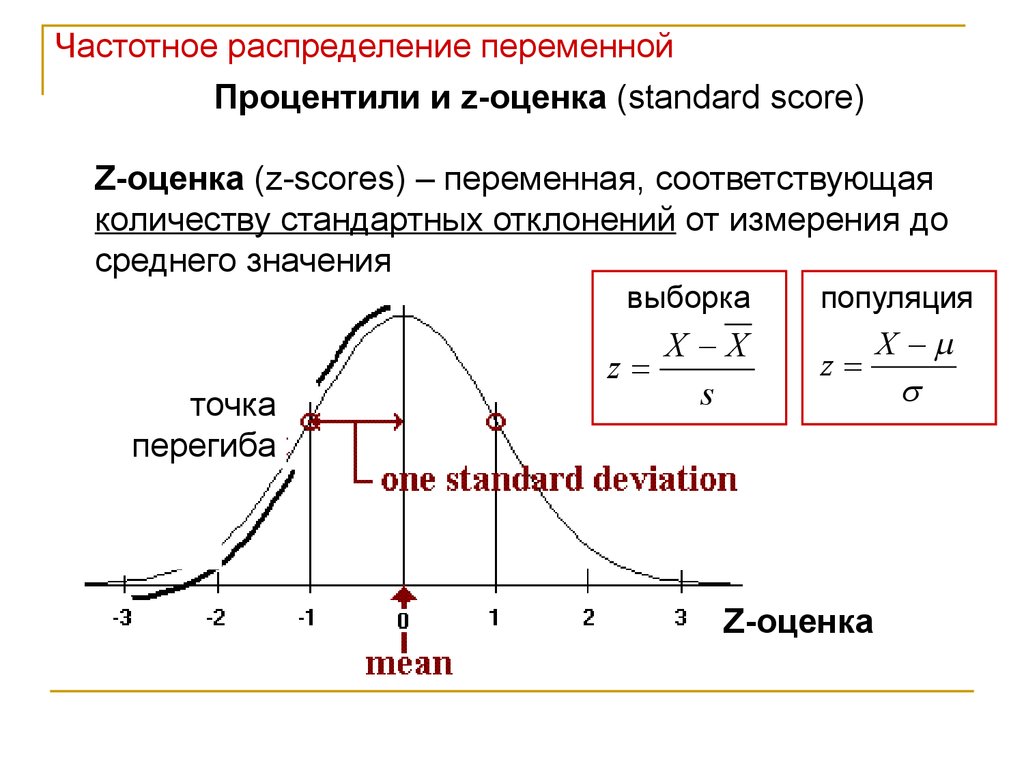
Частотное распределение переменнойПроцентили и z-оценка (standard score)
Z-оценка (z-scores) – переменная, соответствующая
количеству стандартных отклонений от измерения до
среднего значения
выборка
точка
перегиба
X X
z
s
популяция
z
Z-оценка
X
46.
Частотное распределение переменнойПлощадь нормального распределения
Нормальное распределение определяется лишь 2-мя
параметрами – μ и σ .
1
f
e
2
1 X 2
(
)
2
Необыкновенное свойство:
Относительные площади нормального распределения
над одинаковым количеством стандартных отклонений
всегда одинаковы!
47.
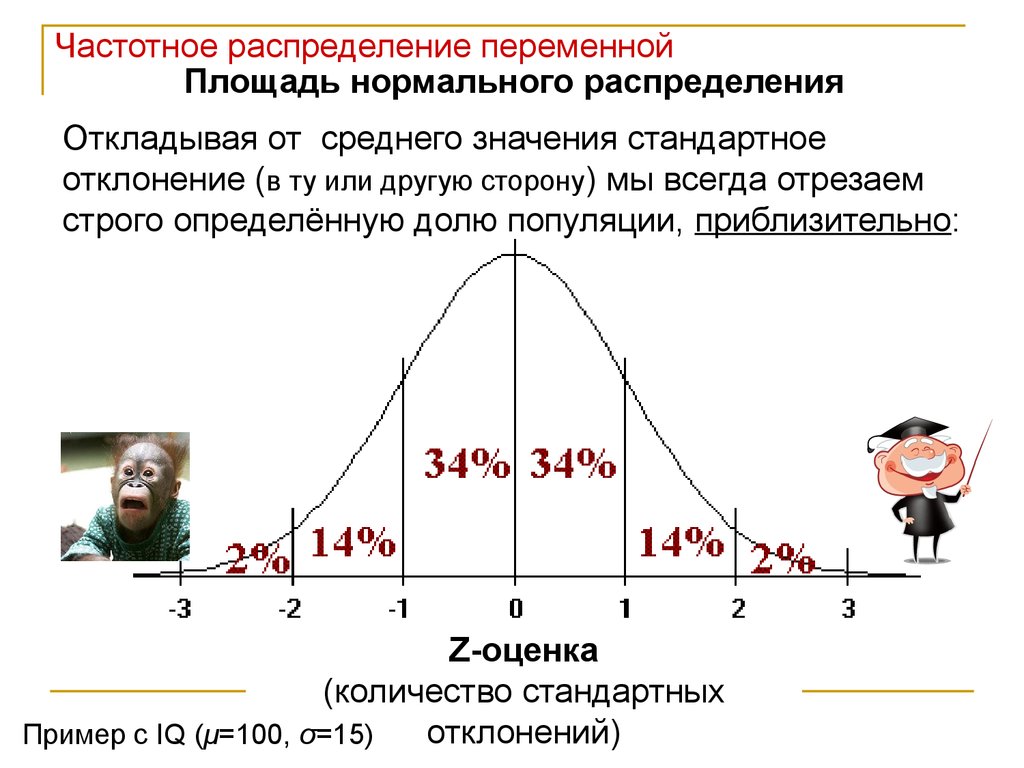
Частотное распределение переменнойПлощадь нормального распределения
Откладывая от среднего значения стандартное
отклонение (в ту или другую сторону) мы всегда отрезаем
строго определённую долю популяции, приблизительно:
Z-оценка
(количество стандартных
отклонений)
Пример с IQ (μ=100, σ=15)
48.
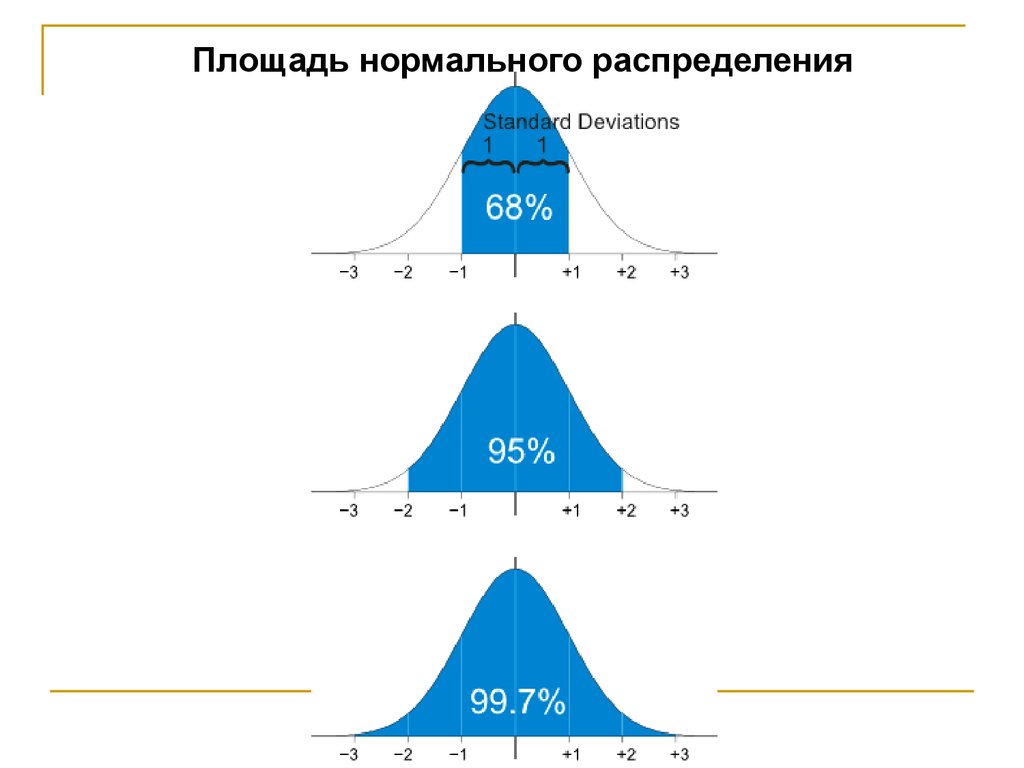
Частотное распределение переменнойПлощадь нормального распределения
49.
Площадь нормального распределения50.
Распределение выборочных средних (sampling distributionof the means)
Три основные концепции в анализе данных:
1. Что такое РАСПРЕДЕЛЕНИЕ переменной и как его
описывать
2. Что такое распределение ВЫБОРОЧНЫХ СРЕДНИХ
и как оно связано с распределением переменной
3. Что такое СТАТИСТИКА КРИТЕРИЯ
выборка
популяция
51.
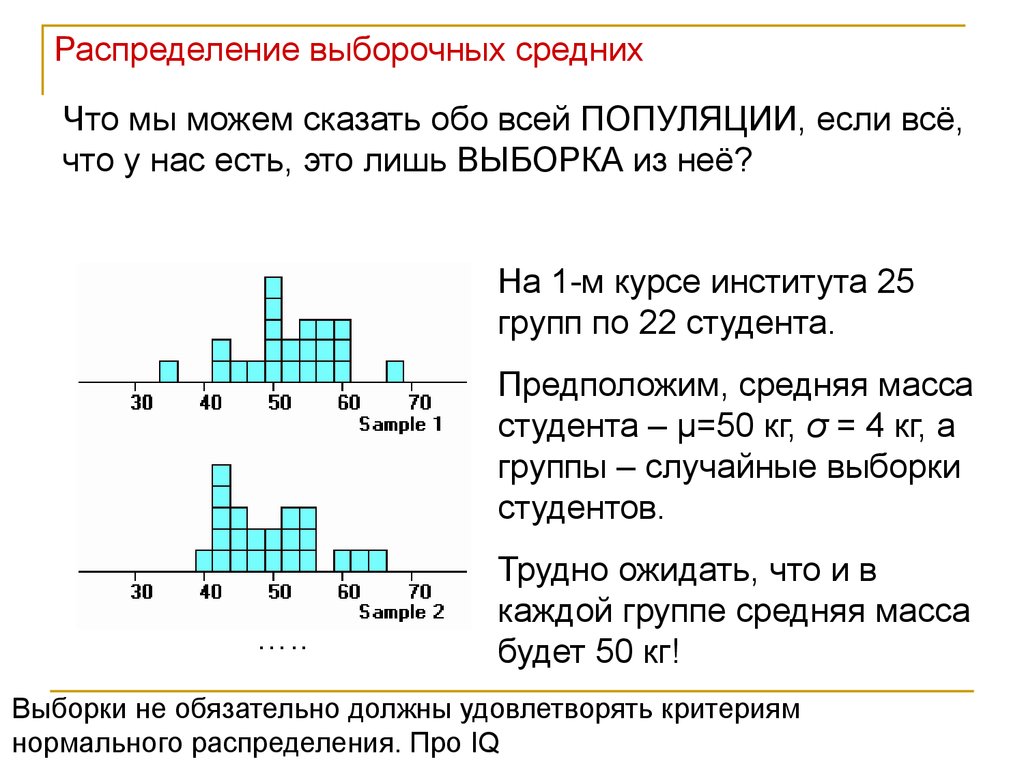
Распределение выборочных среднихЧто мы можем сказать обо всей ПОПУЛЯЦИИ, если всё,
что у нас есть, это лишь ВЫБОРКА из неё?
На 1-м курсе института 25
групп по 22 студента.
Предположим, средняя масса
студента – μ=50 кг, σ = 4 кг, а
группы – случайные выборки
студентов.
…..
Трудно ожидать, что и в
каждой группе средняя масса
будет 50 кг!
Выборки не обязательно должны удовлетворять критериям
нормального распределения. Про IQ
52.
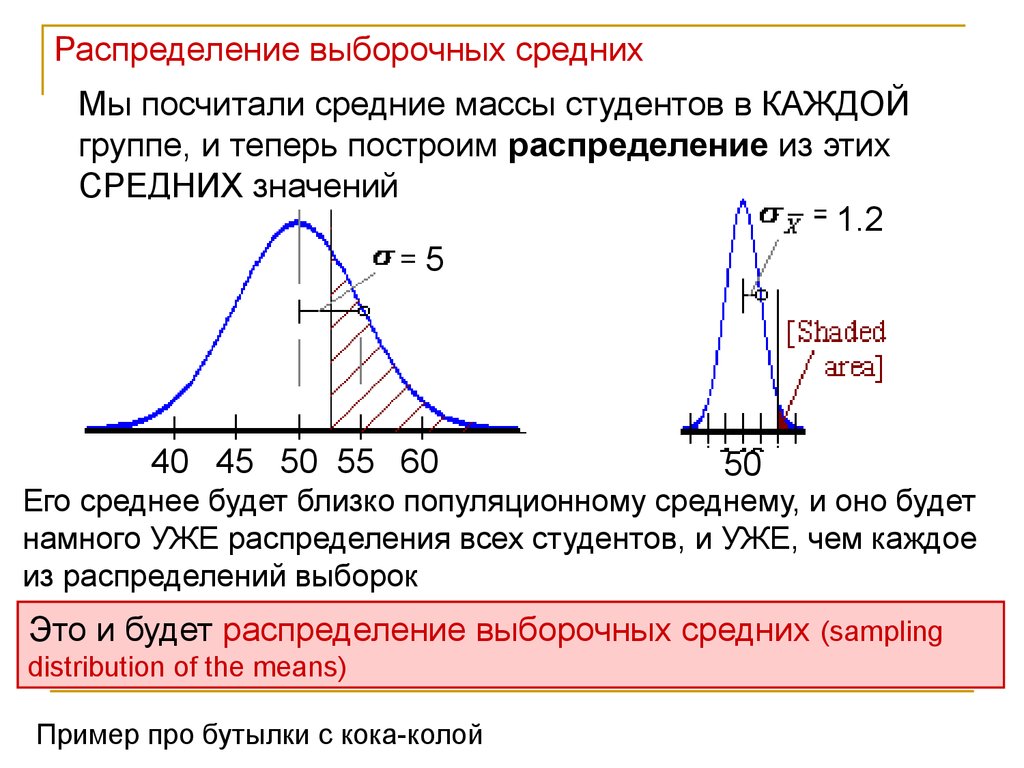
Распределение выборочных среднихМы посчитали средние массы студентов в КАЖДОЙ
группе, и теперь построим распределение из этих
СРЕДНИХ значений
1.2
5
40 45 50 55 60
50
Его среднее будет близко популяционному среднему, и оно будет
намного УЖЕ распределения всех студентов, и УЖЕ, чем каждое
из распределений выборок
Это и будет распределение выборочных средних (sampling
distribution of the means)
Пример про бутылки с кока-колой
53.
Распределение выборочных среднихПопуляция
(все студенты)
стандартное
отклонение
среднее
SE X
n
Выборка
(группа)
Распределение
выборочных средних
X
X
s
>>
X
Стандартная
ошибка среднего
(Standard error = SE)
Чтобы уменьшить ошибку среднего, можно либо
уменьшить дисперсию, либо увеличить размер выборки!
54.
Распределение выборочных среднихЦЕНТРАЛЬНАЯ ПРЕДЕЛЬНАЯ ТЕОРЕМА
Определяет форму, среднее и разброс в
распределении выборочных средних
• Форма: с увеличение размера выборок (групп)
распределение выборочных средних приближается к
нормальному распределению (независимо от формы
распределения популяции).
• Среднее: среднее значение в распределении средних
равно среднему значению в популяции, т.е., X
• Разброс: распределение выборочных средних Уже
распределения популяции на n , где n – объём выборки,
т.е.
Пример с монеткой
55.
Распределение выборочных среднихСледствие:
если некоторая величина отклоняется от среднего под
воздействием слабых, независимых друг от друга
факторов, она имеет нормальное распределение.
Поэтому оно так широко распространено в природе!
56.
Распределение выборочных среднихМасса кролика определяет многими факторами:
Генотип – 7 кг
Уход и любовь
хозяина – 25 кг
Внутриутробные
условия – 5 кг
Качество
вскармливания
мамой – 8 кг
Питание – 20 кг
Т.е., масса кролика – среднее по выборке многих
гипотетических масс. А массы нескольких кроликов –
выборочные средние
57.
Распределение выборочных среднихКак оценить популяционное среднее имея выборку?
У нас есть одна выборка. Из неё мы получили среднее значение
X
Насколько оно близко среднему значению в популяции (μ)?
Решим обратную задачу. Пусть нам известно μ, найдём X
Мы знаем, что для нормального распределения есть z-оценка,
значениям которой соответствуют определённые площади
распределения.
Но мы также знаем, что выборочные средние образуют
нормальное распределение!!
Это значит, что, зная среднее в популяции, мы можем
рассчитать интервал, в который попадёт выборочное
среднее с вероятностью, скажем, в 95% (или 99%).
58.
Распределение выборочных средних1.2
5
-2
-1
0
1
2 Z - оценка
0
Z - оценка
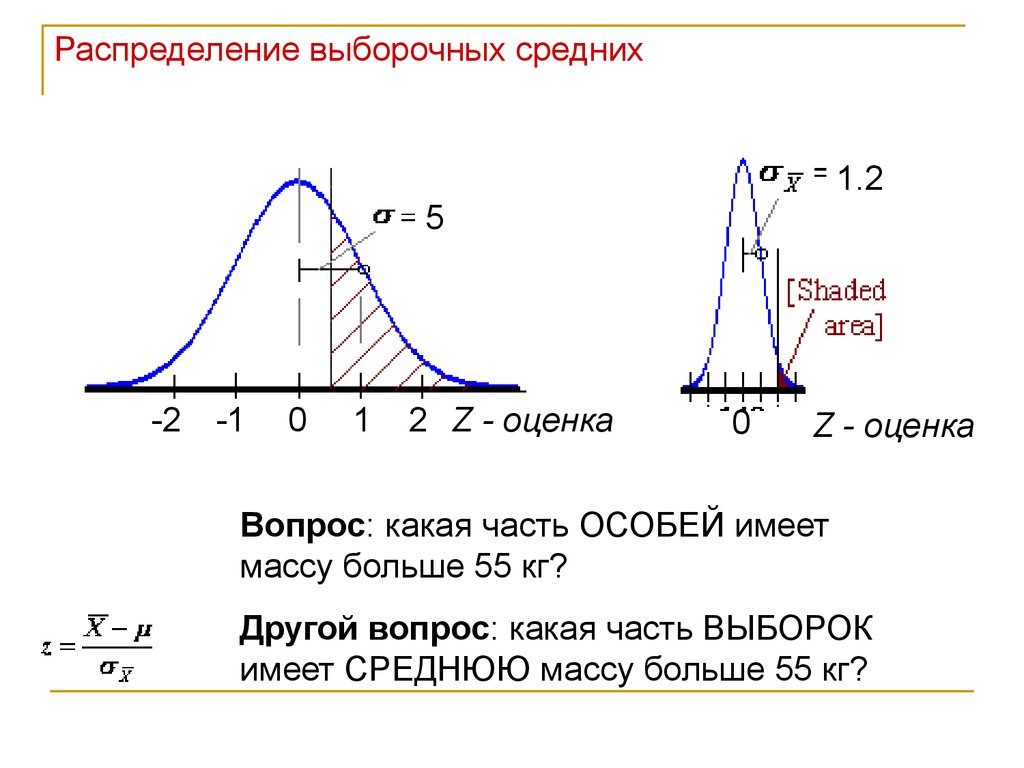
Вопрос: какая часть ОСОБЕЙ имеет
массу больше 55 кг?
Другой вопрос: какая часть ВЫБОРОК
имеет СРЕДНЮЮ массу больше 55 кг?
59.
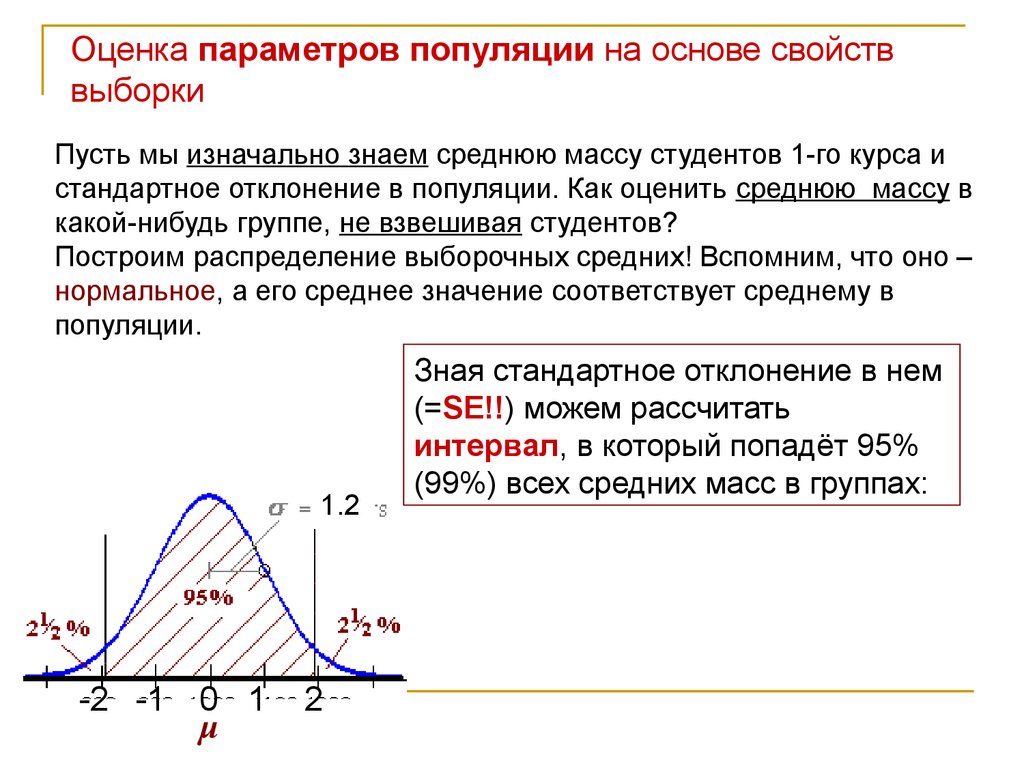
Оценка параметров популяции на основе свойстввыборки
Пусть мы изначально знаем среднюю массу студентов 1-го курса и
стандартное отклонение в популяции. Как оценить среднюю массу в
какой-нибудь группе, не взвешивая студентов?
Построим распределение выборочных средних! Вспомним, что оно –
нормальное, а его среднее значение соответствует среднему в
популяции.
1.2
-2 -1 0 1
μ
2
Зная стандартное отклонение в нем
(=SE!!) можем рассчитать
интервал, в который попадёт 95%
(99%) всех средних масс в группах:
60.
Оценка параметров популяции на основе свойстввыборки
95% доверительный интервал (95% confidence interval):
интервал значений переменной, который с вероятностью
95% содержит нужный параметр.
Т.е., расстояние от среднего значения в популяции до
выборочного среднего для 95% выборок не больше 1.96 SE
Вернёмся к исходной задаче:
Как оценить среднюю массу в популяции, если нам
известно среднее в выборке??
Расстояние от среднего в выборке до (неизвестного)
среднего в популяции с вероятностью 95% не больше
1.96 SE
zcv0.05 1.96
cv – critical value, критическое значение статистики (в
данном случае, Z) – грубо говоря, вероятность ошибки.
61.
Оценка параметров популяции на основе свойстввыборки
Вопрос: где расположено μ?
Ответ: я точно не знаю, но наиболее вероятно – в
пределах ± 2-х стандартных ошибок среднего (SE)
X zcv0.05 SE X zcv0.05 SE
Чем больше уровень достоверности – 99%, 99,9%...
доверительный уровень) тем ШИРЕ будет интервал
Вопрос: где расположено μ?
Ответ: я совершенно уверен, что оно лежит в
пределах... от
до
В примере нам было известно σ, но на
практике оно обычно неизвестно!
(=
62.
Оценка параметров популяции на основе свойстввыборки
Мы не знаем стандартное отклонение в популяции, и
оцениваем его через стандартное отклонение в выборке
– поэтому, доверительный интервал должен быть ШИРЕ,
чем при известном σ.
Насколько шире? Это будет зависеть от РАЗМЕРА
ВЫБОРКИ (от числа степеней свободы df = n-1)
s
(X
i
X)
2
i
n 1
df
s
SE s X
n
Пояснить про число степеней свободы
(x
i
)
i
n
2
63.
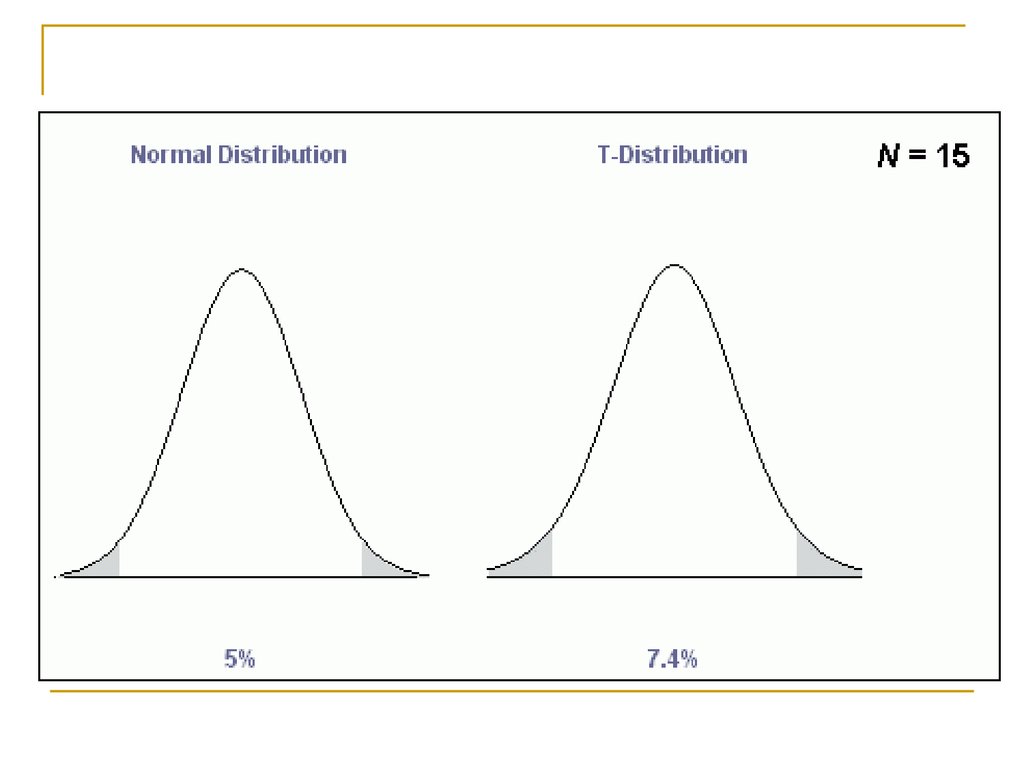
t-распределение (Стьюдента)t df
df=k
При больших (>30) размерах выборок приближается к
нормальному
64.
65.
Для публикацийиногда стандартную ошибку среднего приводят как
показатель разброса в выборке (±SE); это не очень
корректно, т.к. это характеристика не выборки, а
выборки выборочных средних;
зато в публикациях нередко используют
доверительный интервал (95% CI), ведь он показывает
местонахождение популяционного среднего;
66.
В чём ошибки?67.
Темы занятий (2015 год)1. Основные понятия. Описательная статистика
2. Тестирование гипотез в статистике. Критерии Стьюдента
3. Мощность статистического теста. Величина различий (effect
size). Формирование выборок для параметрических
критериев.
4. Дисперсионный анализ ANOVA
5. Дисперсионный анализ ANOVA (продолжение)
6. Корреляции. Регрессионный анализ
7. Трансформация данных. Непараметрические критерии.
8. Частотный анализ.
9. Основы многомерных методов анализа. Факторный анализ.
10. Дискриминантный анализ. Многомерное шкалирование.
Кластерный анализ















































 Математика
Математика








