Задачи на построение

1.

ЗАДАЧИ НА ПОСТРОЕНИЕ
При решении задач на построение мы будем
использовать основные задачи на построение, которые
были рассмотрены ранее. Они называются
простейшими построениями.
К ним относятся:
- построение середины отрезка
- построение биссектрисы угла
- построение угла равного данному
- построение прямой , перпендикулярной данной и
проходящей через точку лежащую (не лежащую) на
данной прямой.
Решая далее задачи на построение мы будем
указывать данные построения, не расписывая подробно
их по шагам

2.

Построение
прямоугольного
треугольника
по двум катетам

3.

Дано:
a
b
Построить:
Прямоугольн
ый АВС,
у которого
катет АС=a,
катет ВС=b.

4.

Дано:
a
b
m
Построить:
Прямоугольн
ый АВС,
у которого
катет АС=a,
катет ВС=b.
Построение:
1) Строим произвольную
прямую m.

5.

Дано:
a
b
С
Построить:
Прямоугольн
ый АВС,
у которого
катет АС=a,
катет ВС=b.
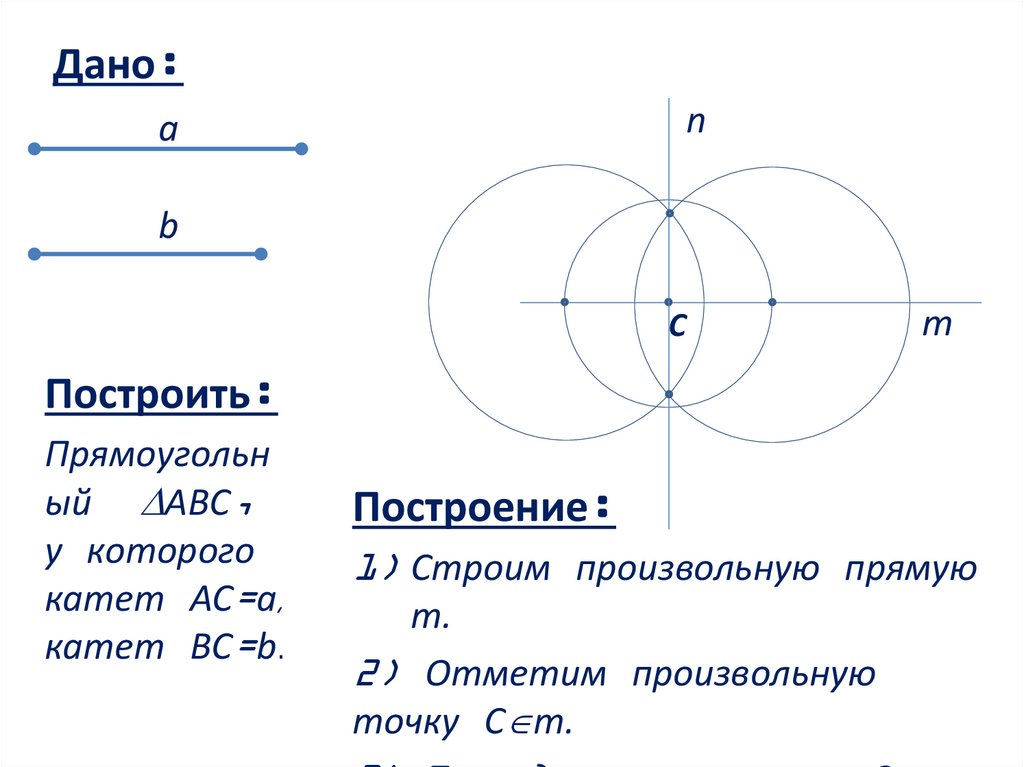
Построение:
1) Строим произвольную
прямую m.
2) Отметим произвольную
точку С m.
m

6.

Дано:
n
a
b
С
m
Построить:
Прямоугольн
ый АВС,
у которого
катет АС=a,
катет ВС=b.
Построение:
1) Строим произвольную прямую
m.
2) Отметим произвольную
точку С m.

7.

А
Дано:
n
a
b
С
Построить:
Прямоугольн
ый АВС,
у которого
катет АС=a,
катет ВС=b.
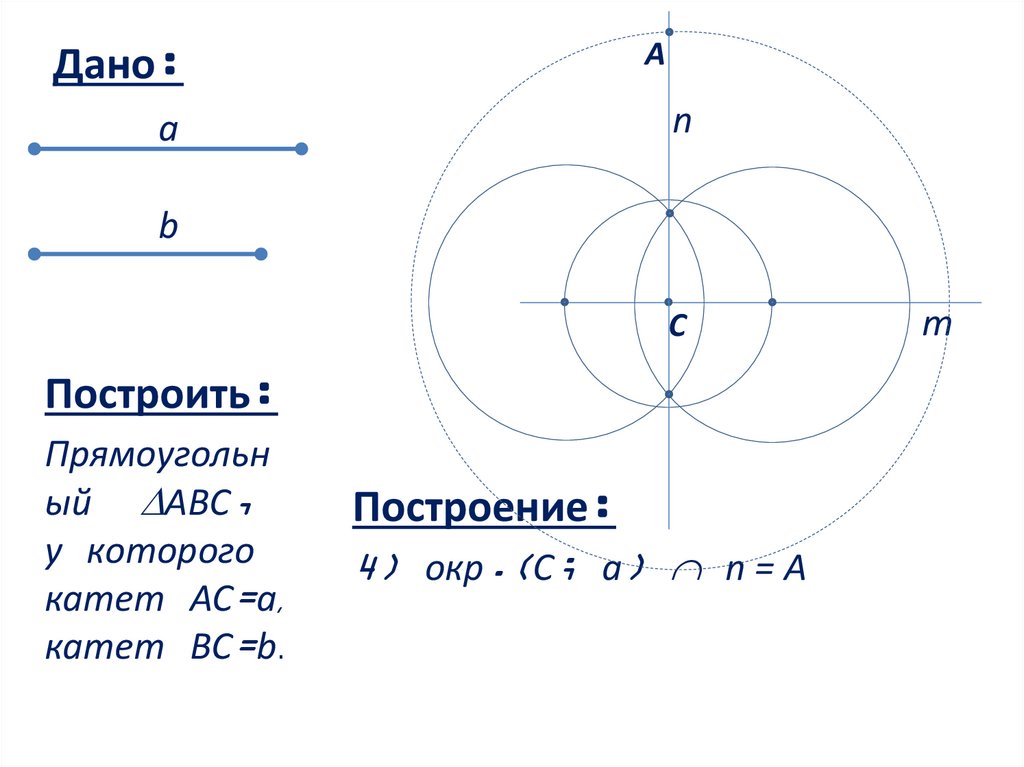
Построение:
4) окр.(С; a) n = А
m

8.

А
Дано:
n
a
b
С
Построить:
Прямоугольн
ый АВС,
у которого
катет АС=a,
катет ВС=b.
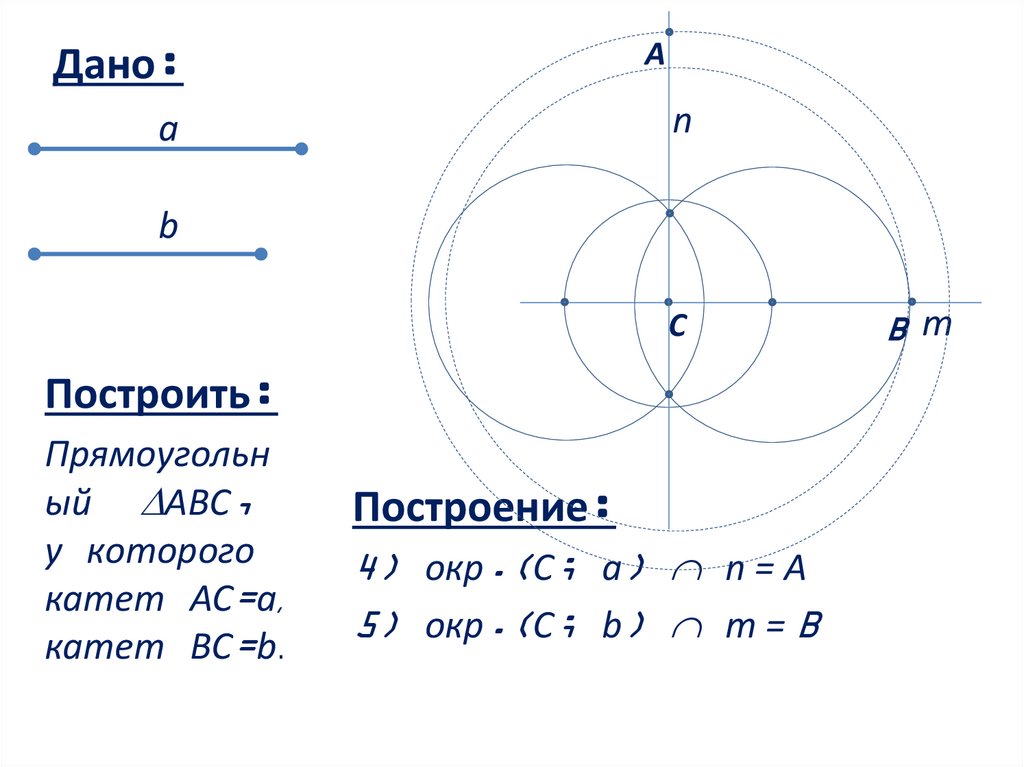
Построение:
4) окр.(С; a) n = А
5) окр.(С; b) m = B
B m

9.

А
Дано:
n
a
b
С
Построить:
Прямоугольн
ый АВС,
у которого
катет АС=a,
катет ВС=b.
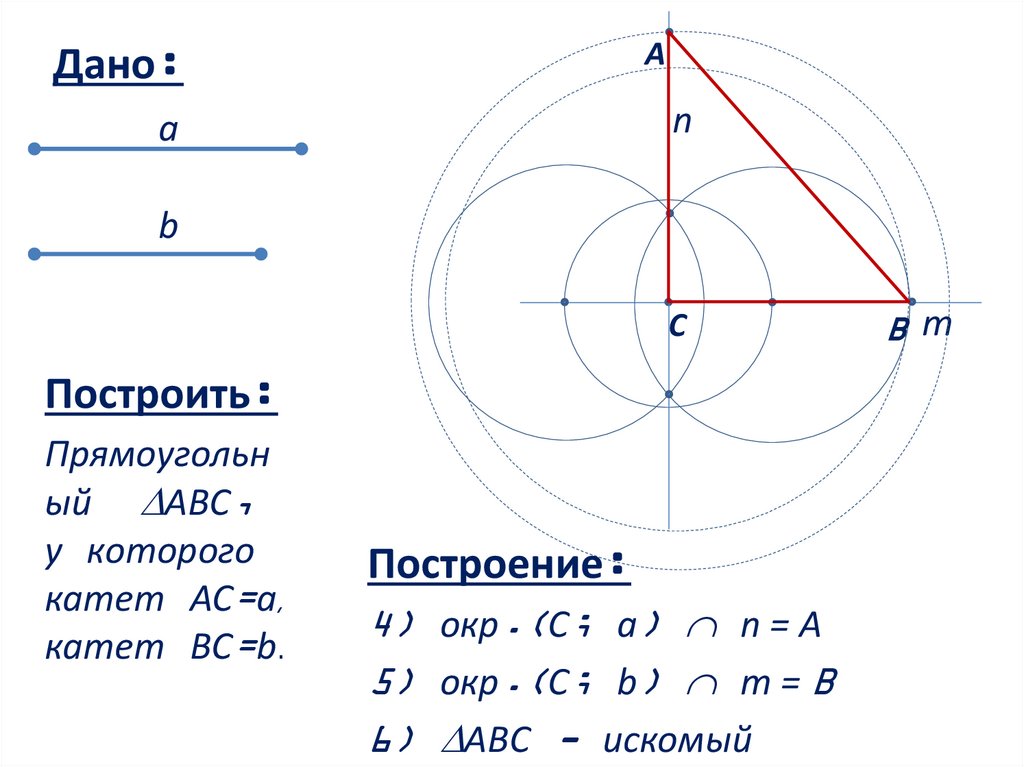
Построение:
4) окр.(С; a) n = А
5) окр.(С; b) m = B
6) АВС - искомый
B m

10.

Дано:
a
А
n
b
С
B m
Построить:
Прямоугольн
ый АВС,
у которого
катет АС=a,
катет ВС=b.
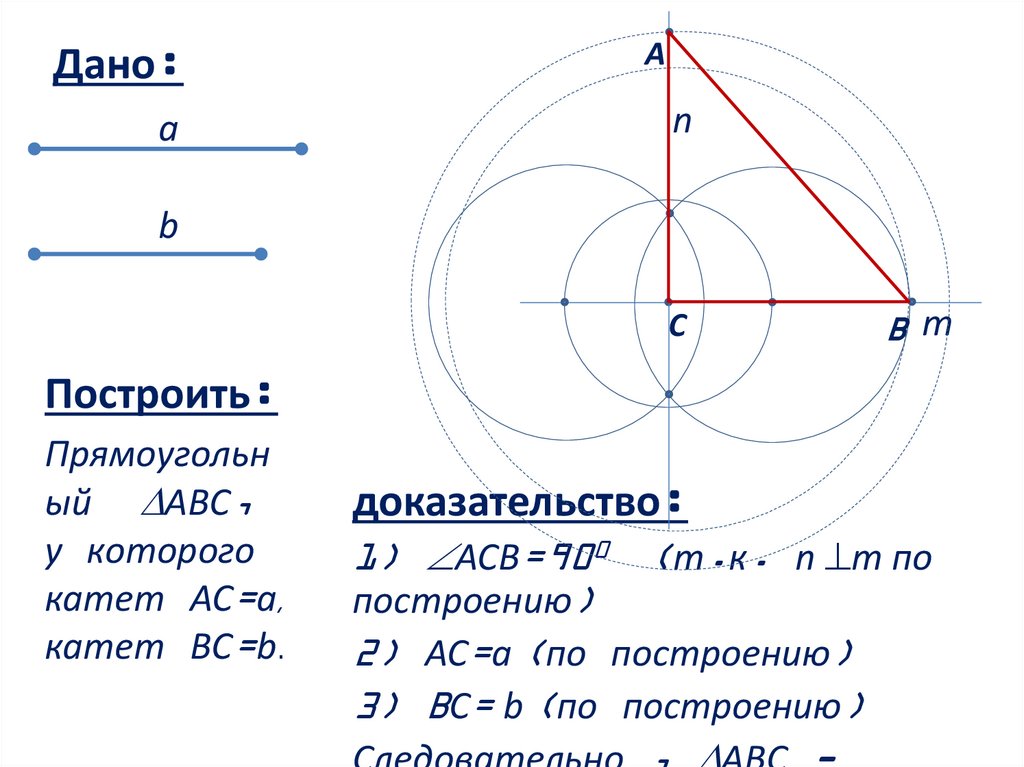
доказательство:
1) АСВ=900 (т.к. n m по
построению)
2) АС=a (по построению)
3) BС= b (по построению)

11.

Дано:
А
n
a
b
С
Построить:
Прямоугольн
ый АВС,
у которого
катет АС=a,
катет ВС=b.
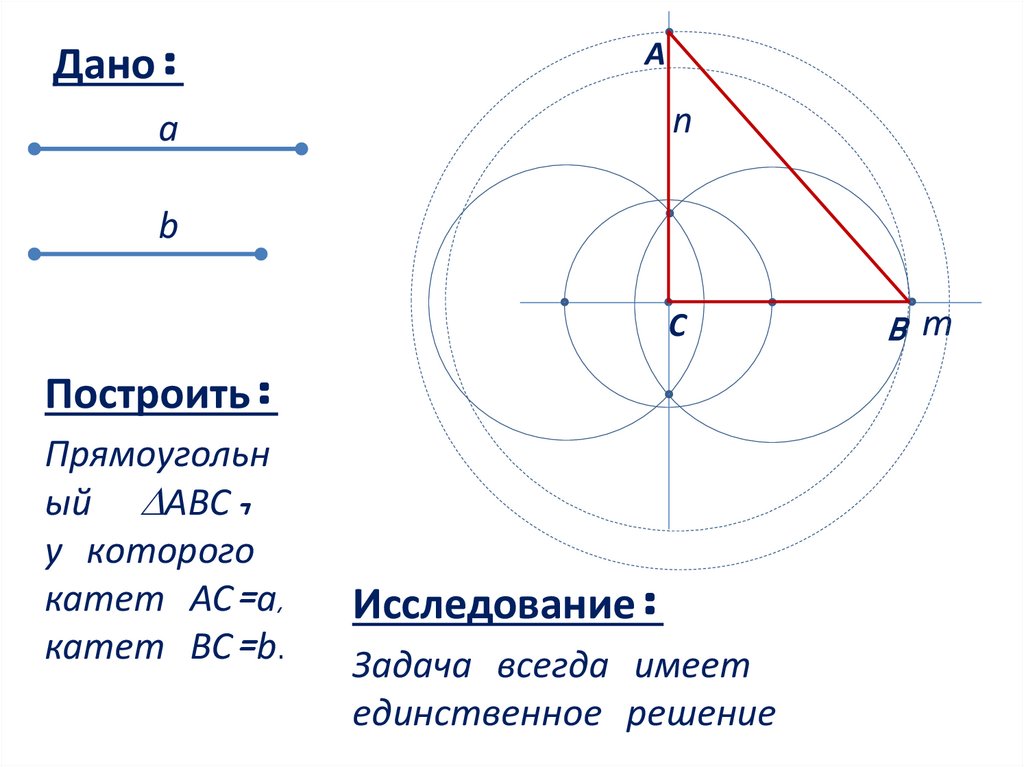
Исследование:
Задача всегда имеет
единственное решение
B m

12.

Построение
прямоугольного
треугольника
по катету и острому
углу

13.

Дано:
a
Построить:
Прямоугольн
ый АВС,
у которого
катет АС=a,
прилежащий
к нему
острый

14.

Дано:
a
m
Построить:
Прямоугольн
ый АВС,
у которого
катет АС=a,
прилежащий
к нему
острый
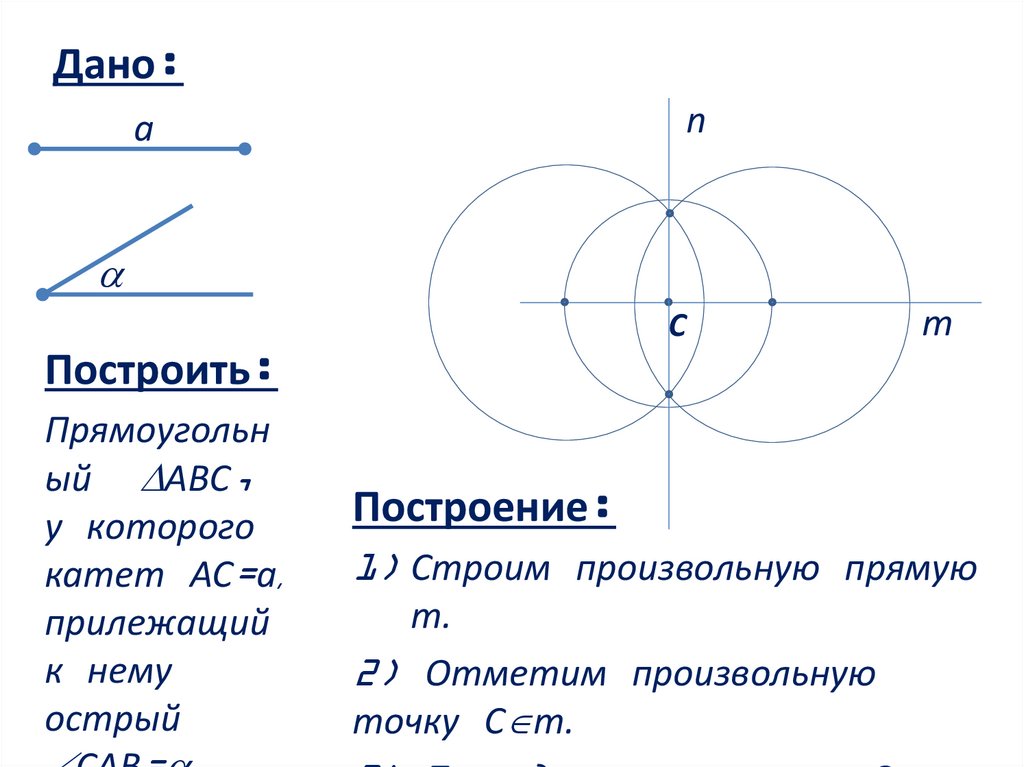
Построение:
1) Строим произвольную
прямую m.

15.

Дано:
a
С
Построить:
Прямоугольн
ый АВС,
у которого
катет АС=a,
прилежащий
к нему
острый
Построение:
1) Строим произвольную
прямую m.
2) Отметим произвольную
точку С m.
m

16.

Дано:
n
a
С
m
Построить:
Прямоугольн
ый АВС,
у которого
катет АС=a,
прилежащий
к нему
острый
Построение:
1) Строим произвольную прямую
m.
2) Отметим произвольную
точку С m.

17.

Дано:
А
n
a
С
Построить:
Прямоугольн
ый АВС,
у которого
катет АС=a,
прилежащий
к нему
острый
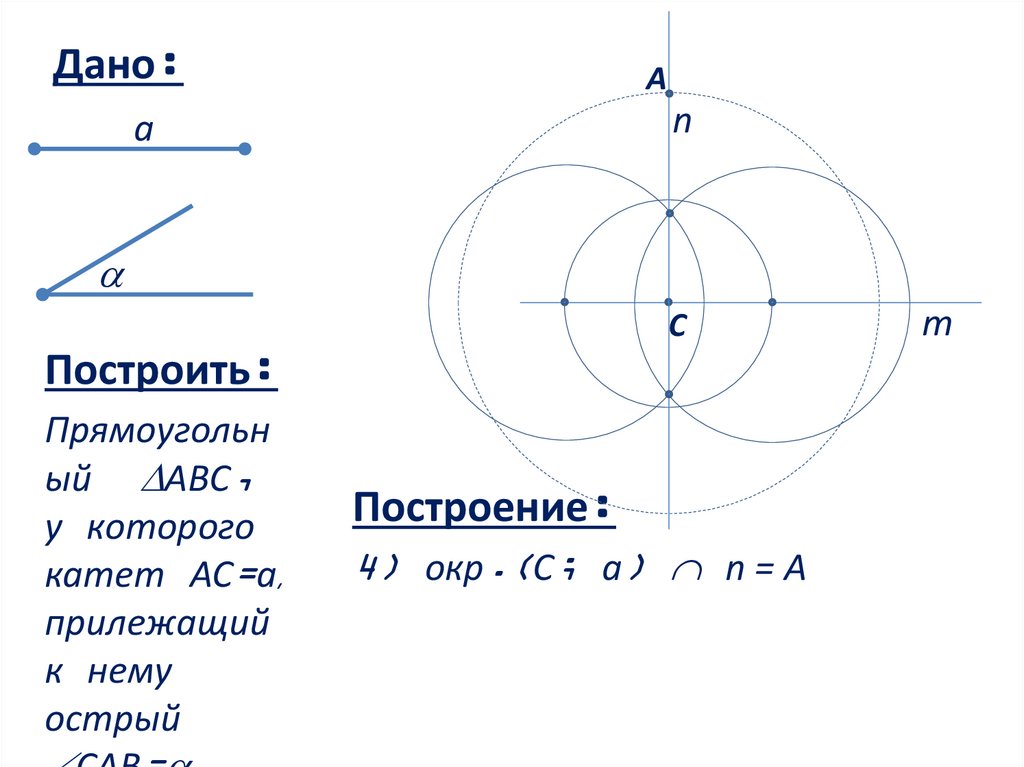
Построение:
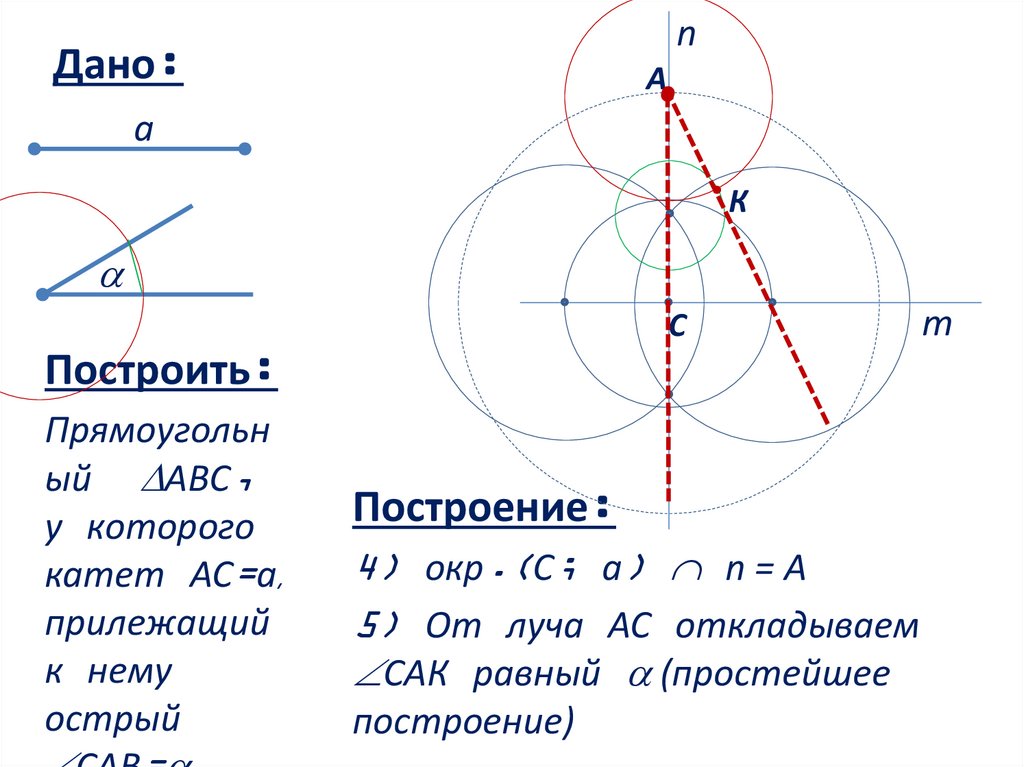
4) окр.(С; a) n = А
m

18.

n
Дано:
А
a
К
С
Построить:
Прямоугольн
ый АВС,
у которого
катет АС=a,
прилежащий
к нему
острый
Построение:
4) окр.(С; a) n = А
5) От луча АС откладываем
САК равный (простейшее
построение)
m

19.

n
Дано:
А
a
К
С
B
Построить:
Прямоугольн
ый АВС,
у которого
катет АС=a,
прилежащий
к нему
острый
Построение:
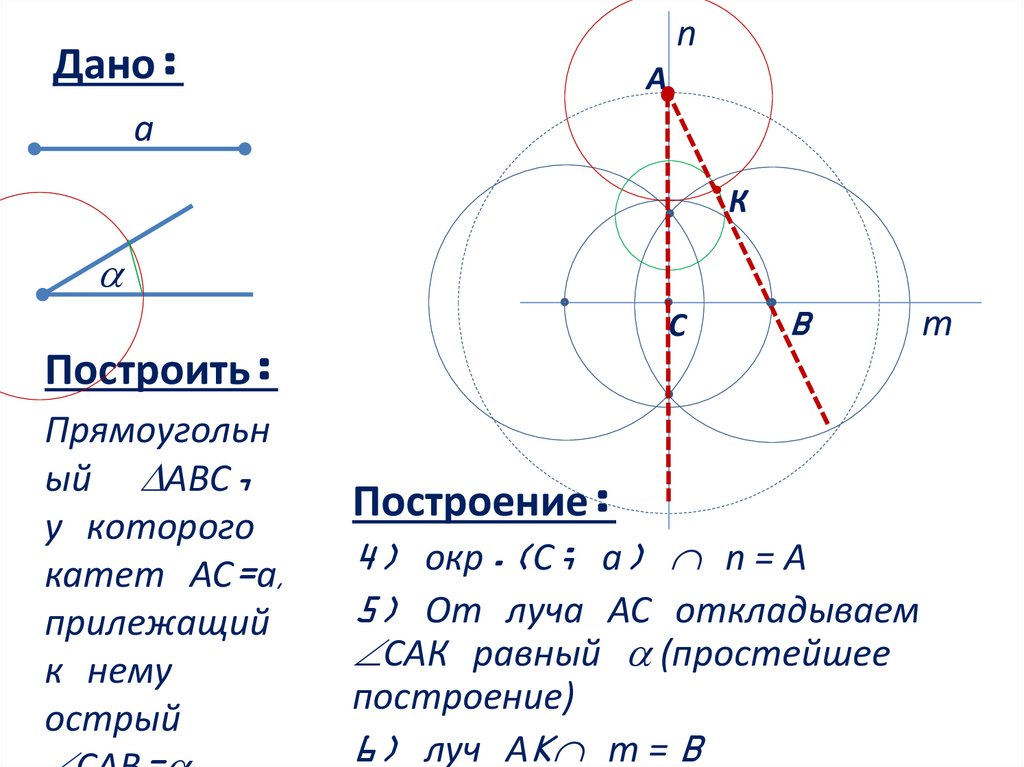
4) окр.(С; a) n = А
5) От луча АС откладываем
САК равный (простейшее
построение)
6) луч АK m = B
m

20.

n
Дано:
А
a
К
С
B
m
Построить:
Прямоугольн
ый АВС,
у которого
катет АС=a,
прилежащий
к нему
острый
Построение:
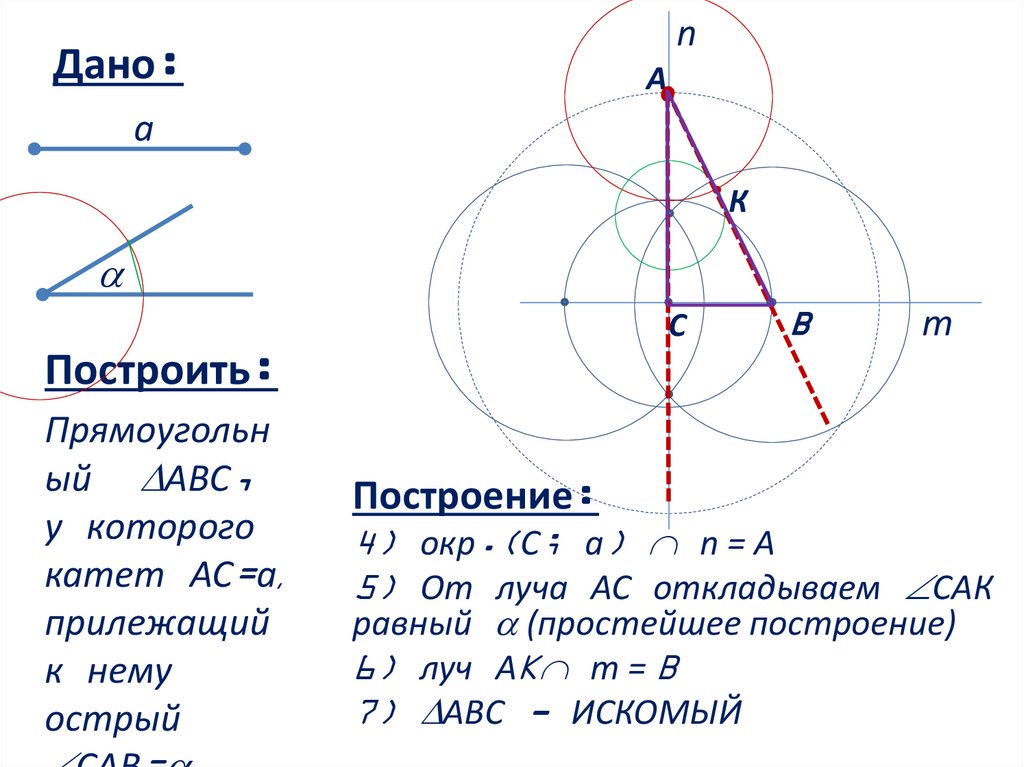
4) окр.(С; a) n = А
5) От луча АС откладываем САК
равный (простейшее построение)
6) луч АK m = B
7) АВС - ИСКОМЫЙ

21.

Дано:
n
А
a
К
С
B
m
Построить:
Прямоугольн
ый АВС,
у которого
катет АС=a,
прилежащий
к нему
острый
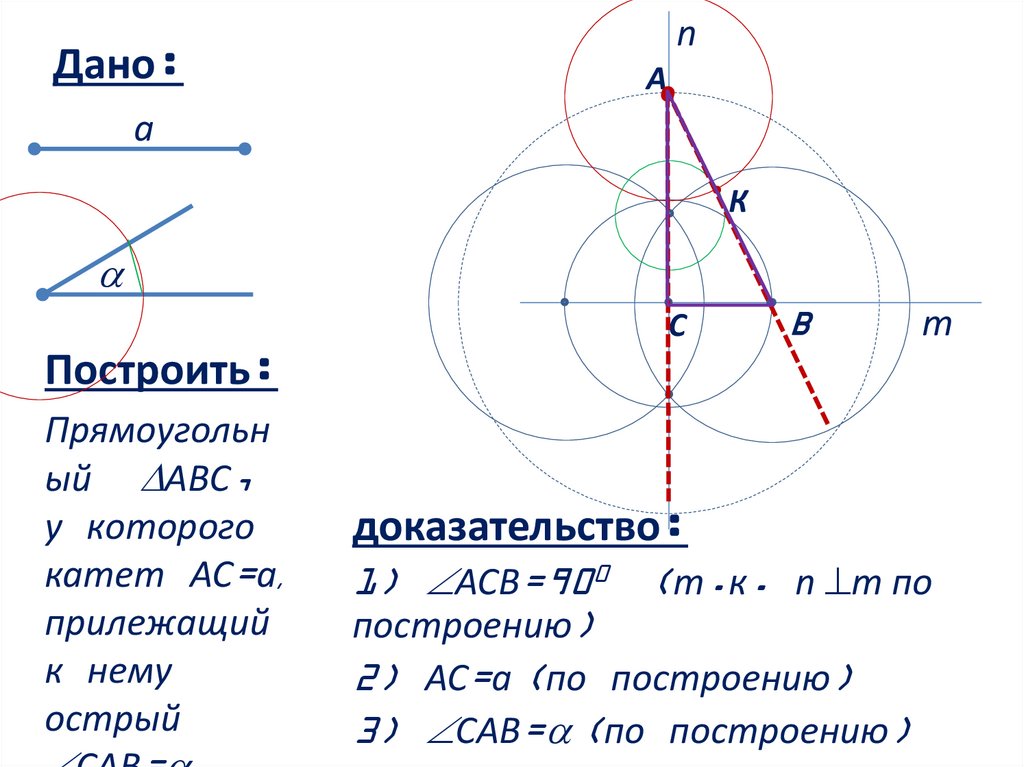
доказательство:
1) АСВ=900 (т.к. n m по
построению)
2) АС=a (по построению)
3) САВ= (по построению)

22.

Дано:
n
А
a
К
С
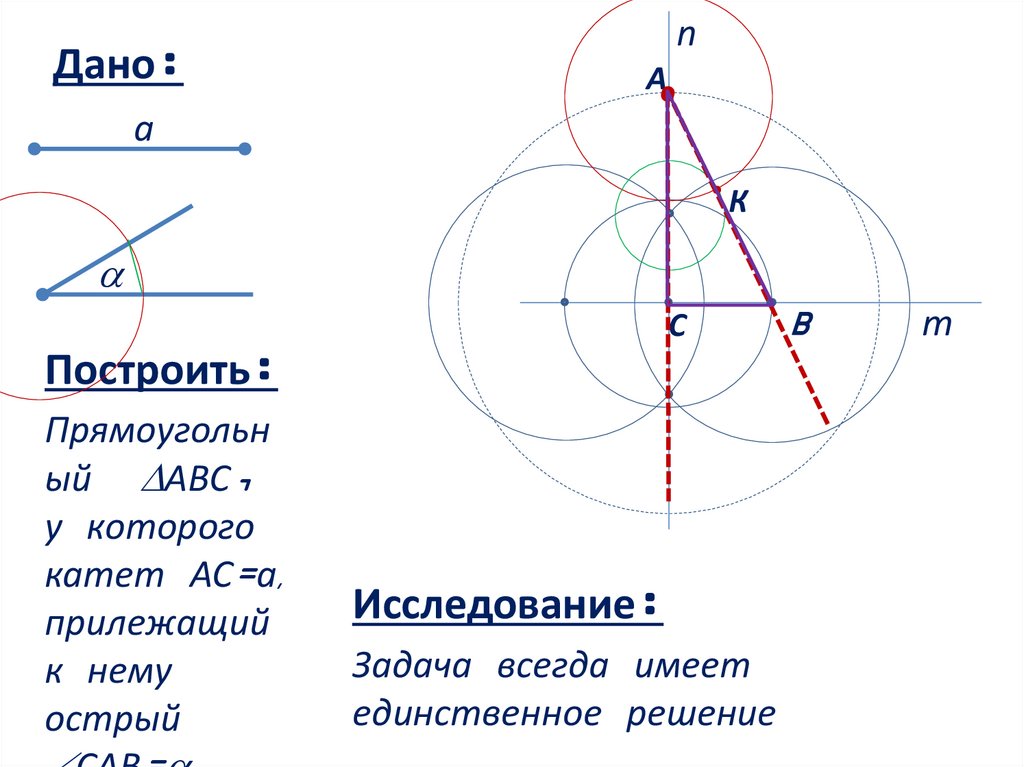
Построить:
Прямоугольн
ый АВС,
у которого
катет АС=a,
прилежащий
к нему
острый
Исследование:
Задача всегда имеет
единственное решение
B
m

23.

Построение
прямоугольного
треугольника
по гипотенузе и
острому углу

24.

Дано:
a
Построить:
Прямоугольн
ый АВС,
у которого
ГИПОТЕНУЗА
ав=a, острый
САВ= .

25.

Дано:
a
m
Построить:
Прямоугольн
ый АВС,
у которого
ГИПОТЕНУЗА
ав=a, острый
САВ= .
Построение:
1) Строим произвольную
прямую m.

26.

Дано:
a
Построить:
Прямоугольн
ый АВС,
у которого
катет АС=a,
прилежащий
к нему
острый
а
Построение:
1) Строим произвольную
прямую m.
2) Отметим произвольную
точку а m.
m

27.

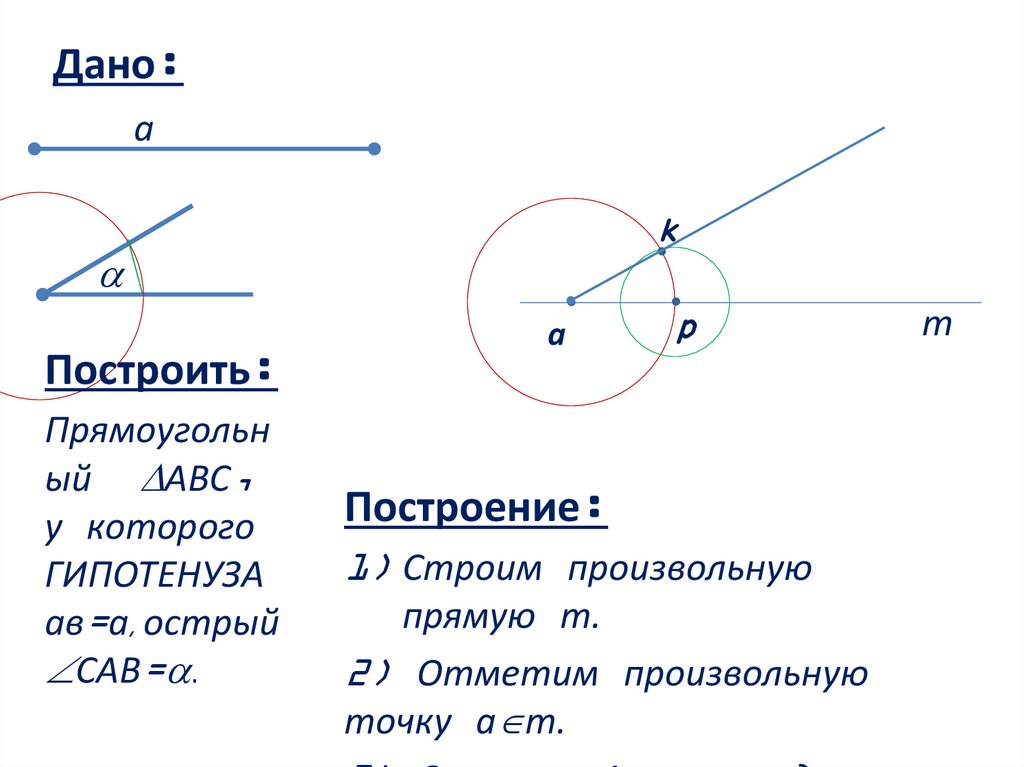
Дано:
a
k
Построить:
Прямоугольн
ый АВС,
у которого
ГИПОТЕНУЗА
ав=a, острый
САВ= .
а
p
Построение:
1) Строим произвольную
прямую m.
2) Отметим произвольную
точку а m.
m

28.

Дано:
В
a
k
Построить:
Прямоугольн
ый АВС,
у которого
ГИПОТЕНУЗА
ав=a, острый
САВ= .
а
p
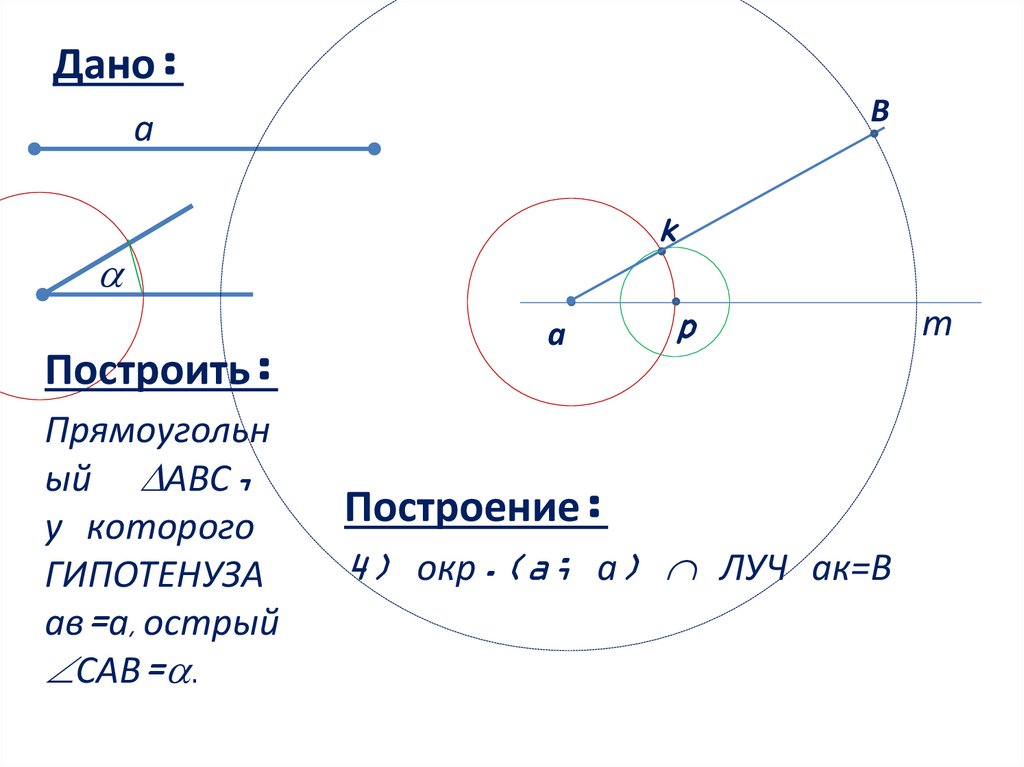
Построение:
4) окр.(a; a) ЛУЧ ак=В
m

29.

Дано:
В
a
k
Построить:
Прямоугольн
ый АВС,
у которого
ГИПОТЕНУЗА
ав=a, острый
САВ= .
C
а
p
m
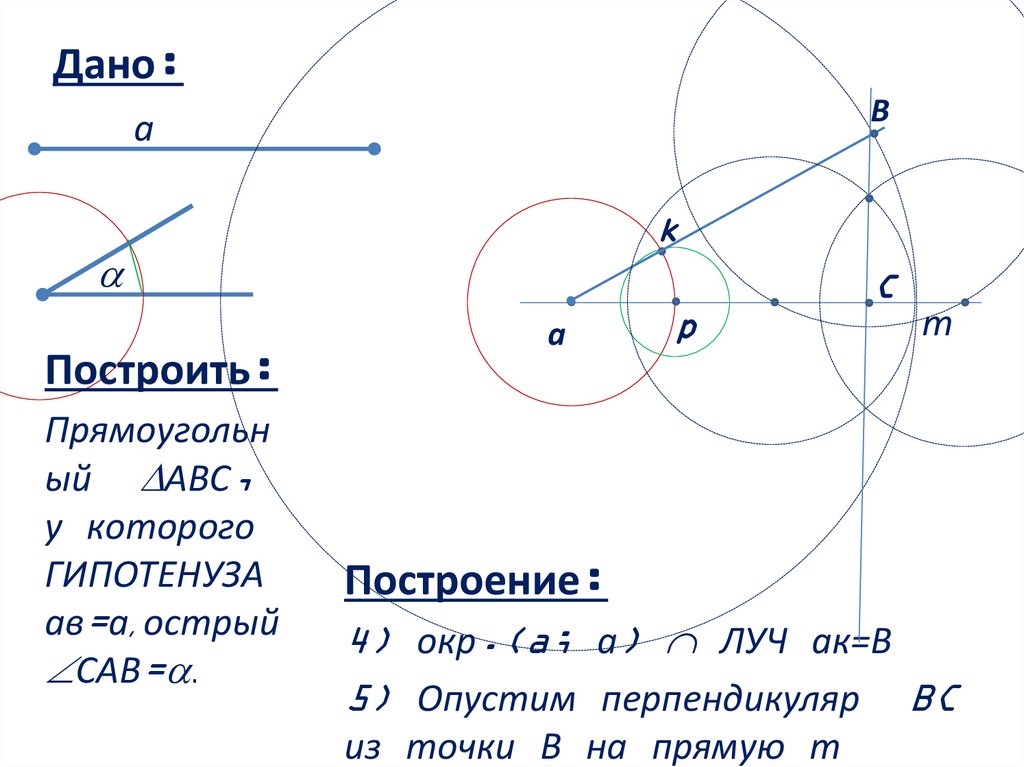
Построение:
4) окр.(a; a) ЛУЧ ак=В
5) Опустим перпендикуляр BC
из точки В на прямую m

30.

Дано:
В
a
k
Построить:
Прямоугольн
ый АВС,
у которого
ГИПОТЕНУЗА
ав=a, острый
САВ= .
C
а
p
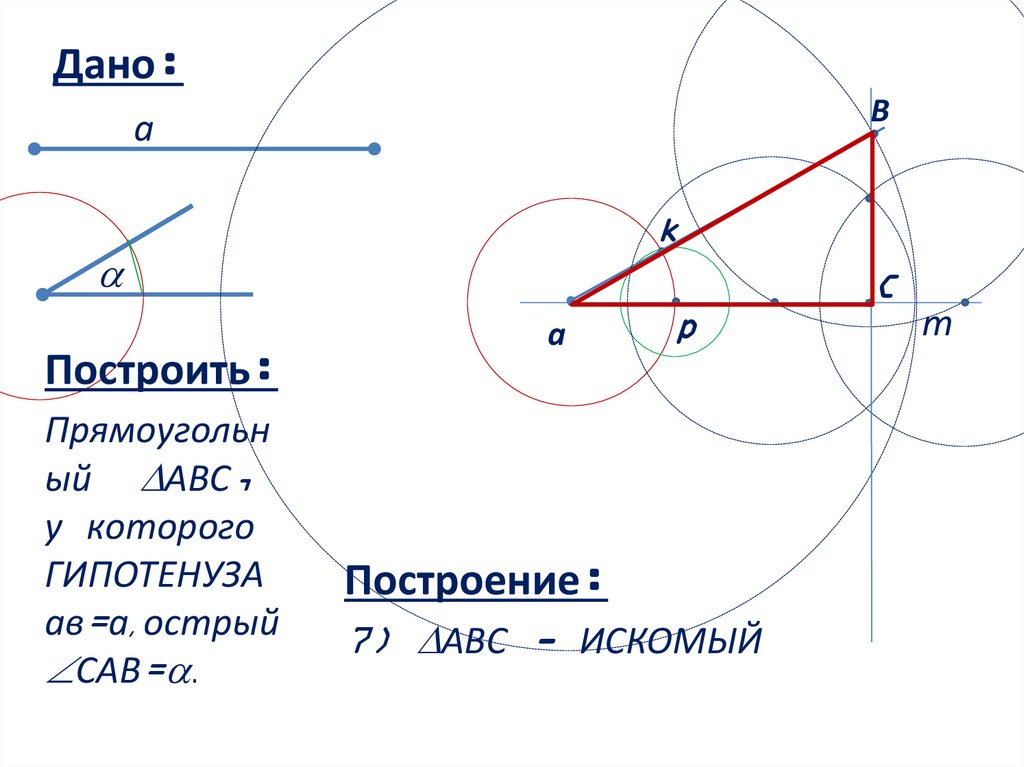
Построение:
7) АВС - ИСКОМЫЙ
m

31.

Дано:
В
a
k
Построить:
Прямоугольн
ый АВС,
у которого
ГИПОТЕНУЗА
ав=a, острый
САВ= .
C
а
p
m
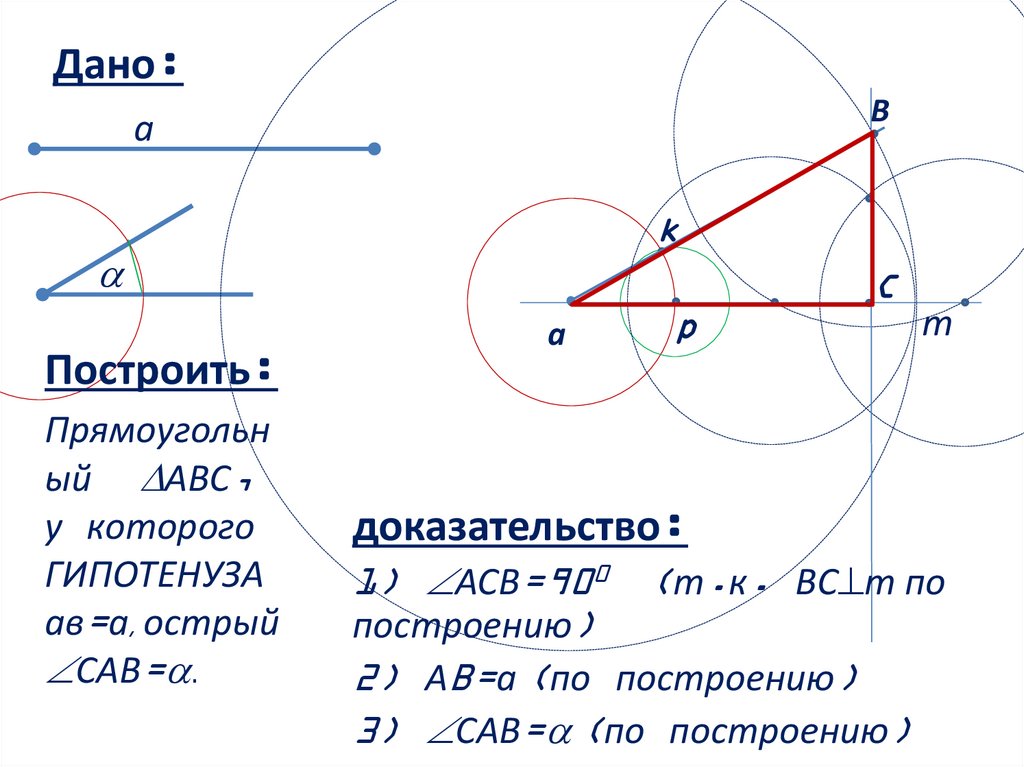
доказательство:
1) АСВ=900 (т.к. BC m по
построению)
2) АB=a (по построению)
3) САВ= (по построению)

32.

Дано:
В
a
k
Построить:
Прямоугольн
ый АВС,
у которого
ГИПОТЕНУЗА
ав=a, острый
САВ= .
C
а
p
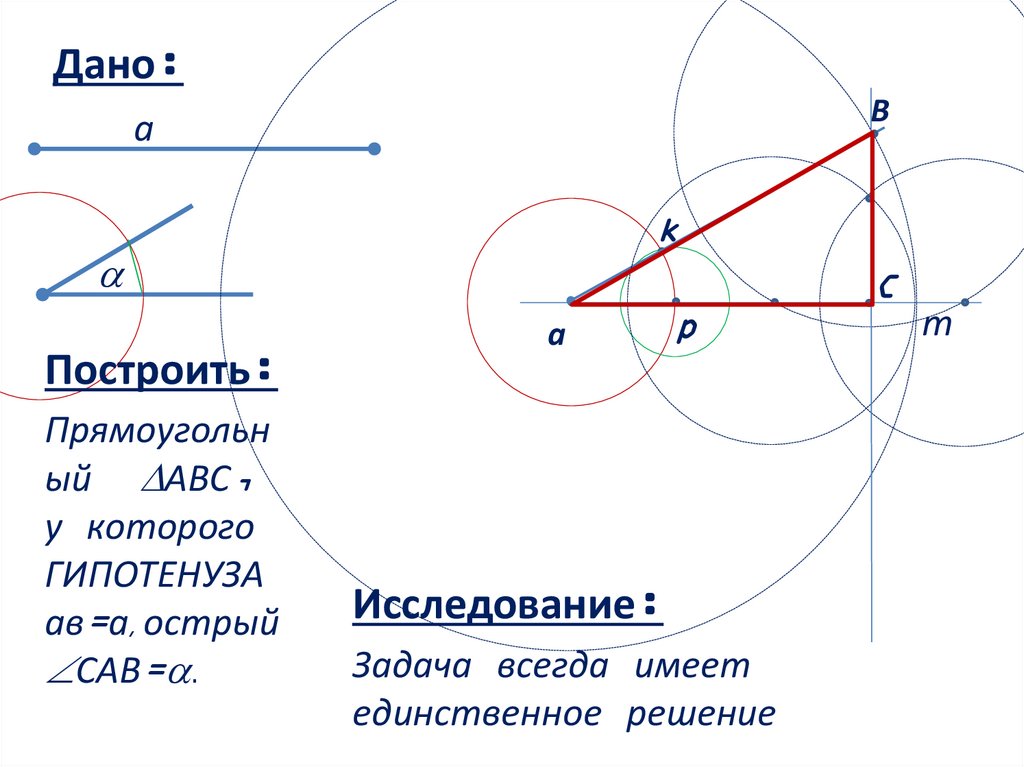
Исследование:
Задача всегда имеет
единственное решение
m