Старинные системы счисления

1. Старинные системы счисления

2. Содержание

1.
2.
3.
4.
5.
6.
7.
8.
Египетская система счисления
Клинопись Вавилона
Цифры индейцев племени майя
Китайские иероглифы
Цифры Древнего Рима
Алфавитное изображение чисел Кириллицей
Славянская глаголическая десятеричная
Древнегреческая ионийская десятеричная
алфавитная
9. Начертание арабских цифр
10. Задания

3. Египетская система счисления

Египтяне придумали эту систему около 5 000 лет тому
назад. Это одна из древнейших систем записи чисел,
известная человеку.

4.

Как и большинство людей, для счета небольшого
количества предметов египтяне использовали
мерные палки.
Например, числа: 1 – | , 2 – || , 3 – ||| , …
Если палочек нужно изобразить больше 5, то их
изображали в два ряда, причем в нижнем
должно быть столько же палочек, сколько и в
верхнем, или на одну больше.
Например, число: 9 – ||||
|||||

5. Иероглифы имели разное начертание и смысл:

6.

Числа, не кратные 10, записывались путем повторения
этих цифр. Каждая цифра могла повторяться от 1 до 9
раз. Например, число 4622 обозначалось следующим
образом:

7. Клинопись Вавилона

В древнем Вавилоне
примерно за 40 веков до
нашего времени была
создана позиционная
нумерация.
В вавилонской поместной
нумерации ту роль, которую
у нас играет число 10, играло
число 60, и потому эту
нумерацию называют
шестидесятеричной.

8.

Числа менее 60 обозначались с помощью двух знаков:
– прямой клин – 1;
-3
- 20
– лежачий клин – 10;
- 32
– ноль.

9.

Для обозначения чисел больше 60 цифры записывались
по разрядам, с небольшими пробелами:
= 3725, то есть 1 х 60 х 60 + 2 х
х 60 + 5;

10. Цифры индейцев племени майя

В начале нашей эры
индейцы племени майя,
которые жили на
полуострове Юкатан в
Центральной Америке,
пользовались другой
позиционной системой
- с основанием 20. Свои
цифры индейцы майя,
как и вавилоняне,
записывали, пользуясь
принципом сложения.

11.

На развитие этой нумерации не повлияла ни одна из
цивилизаций Старого Света.
Сначала эта нумерация обслуживала пятеричную
систему счисления, а потом ее приспособили для
двадцатеричной.

12.

Например, числа:
52 -
, то есть 1+1+5+5+20+20;
16 -
, то есть 1+5+5+5;
23 -
, то есть 1+1+1+20.

13. Китайские иероглифы

Возникла эта нумерация
около 4 000 тысяч лет тому
назад в Китае.
Эта нумерация одна из
самых прогрессивных, в неё
заложены такие же
принципы, как и в
современную арабскую,
которой мы с Вами
пользуемся.

14.

Записывались цифры числа, начиная с больших значений
и заканчивая меньшими.

15.

Например, числа:
548 –
, то есть 5 x 100 + 4 x 10 + 8;
1 000 -
, то есть 1 x 1 000.
Во времена династии Мин был введен знак для пустого
разряда - кружок - аналог нашего нуля.

16. Цифры Древнего Рима

Считается, что цифры
были заимствованы
римлянами скорее всего у
этрусков за 500 лет до
нашей эры .
С этими цифрами мы
достаточно часто
сталкиваемся:
- номера глав в книгах,
- указание века,
- числа на циферблате
часов…

17.

Начертание трех основных цифр:
Следующие цифры обозначались так:
50 – L, 100 – C,
500 – D, 1000 - M

18.

Прежде 1000 изображалась знаком Ф, потому-то 500 и
стал изображать знак D как "половина" Ф.
Так же построены и пары C и L, X и V:

19.

20. Алфавитное изображение чисел Кириллицей

Эта нумерация была создана в IX
веке вместе со славянской
алфавитной системой для
переписки священных книг для
славян греческими монахами
братьями Кириллом
(Константином) и Мефодием.
До сих пор православные
церковные книги используют эту
нумерацию. Для того, чтобы не
перепутать буквы и цифры,
использовались титла горизонтальная черточка над
числами.

21.

22.

Записывались цифры числа, начиная с больших и
заканчивая меньшими, слева направо. Если разряда не
было, то его пропускали.
Например, число: 863 –
Интереснее всего записывались числа второго десятка:
Например, число14 –
Читаем дословно "четырнадцать" - "четыре на десять".
Как слышим, так и пишем: не 10+4, а 4+10, - четыре на
десять. И так для всех чисел от 11 до 19.

23.

Для обозначения чисел больших, чем 900,
использовались специальные значки
, добавляемые
к букве.
Например, числа:

24.

Число 10 000 обозначалось той же буквой, что и 1, только
без титлы, но его обводили кружком. Называлось это
число "тьмой".
Со словом "тьма" связано выражение "тьматьмущая", означающая немыслимо много.
Например, числа:
Аналогично название и обозначение:

25. Славянская глаголическая десятеричная

Славянская
глаголическая десятеричная
Эта система была создана для обозначения чисел в
священных книгах западных славян. Использовалась она
нечасто, но достаточно долго. По организации она в
точности повторяет греческую нумерацию.
Использовалась она с VIII по XIII в.

26.

27.

Числа записывали из цифр так же слева, направо, от
больших к меньшим цифрам. Если десятков, единиц, или
какого-то другого разряда не было, то его пропускали.
Такая запись числа аддитивная, то есть в ней
используется только сложение:
= 800+60+3 = 863
Для того чтобы не перепутать буквы и цифры,
использовались титла - горизонтальные черточки над
числами, или точки.

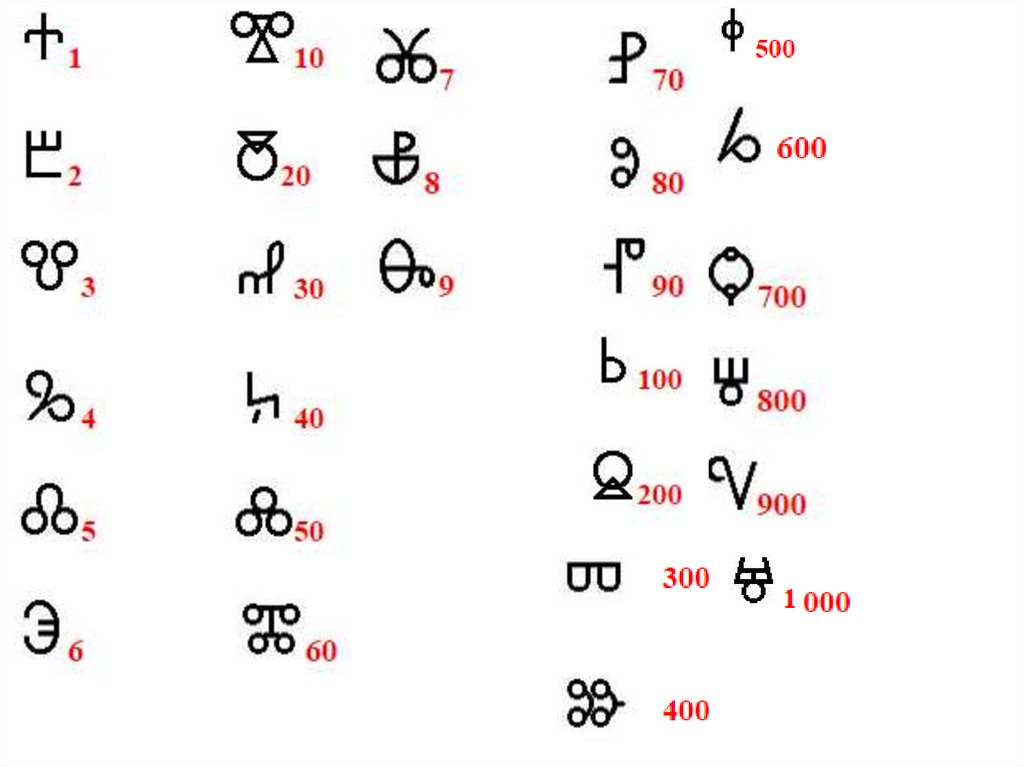
28. Древнегреческая ионийская десятеричная алфавитная

Древнегреческая
ионийская десятеричная алфавитная
Примерно в третьем веке до нашей эры аттическая
система счисления в Греции была вытеснена другой, так
называемой "Ионийской" системой (она возникла в
Милеете – греческая малоазиатская колония Ионии). В
ней числа 1 - 9 обозначаются первыми буквами
древнегреческого алфавита:

29.

числа 10, 20, … 90 изображались следующими девятью
буквами:
числа 100, 200, … 900 последними девятью буквами:
Для обозначения тысяч и десятков тысяч пользовались
теми же цифрами, но только с добавлением особого
значка '. Любая буква с этим значком сразу же
становилась в тысячу раз больше.

30.

Для отличия цифр и букв писали черточки над цифрами.
Древние евреи, арабы и многие другие народы Ближнего
Востока имели такие же системы счисления.
При ее помощи можно было просто записать числа до ста
миллионов (100 000 000). Эта система по быстроте счета
мало отличается от «арабской».

31. Начертание арабских цифр

Начертания цифр и обозначение чисел были созданы в
Индии между II и VI веками. В страны Европы индийская
нумерация была занесена арабами в X –XIII веках. В
России она появилась при Петре I. И поныне сохранилось
название «арабские цифры».
Цифры «губар» мавританских государств
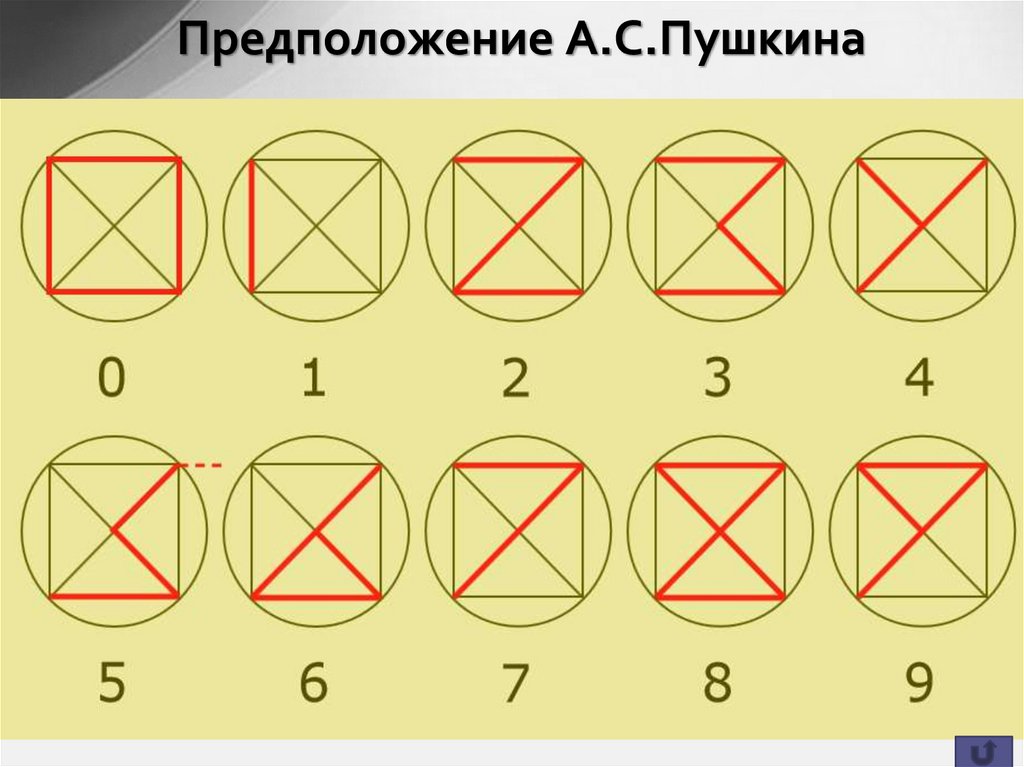
Предположение А.С.Пушкина
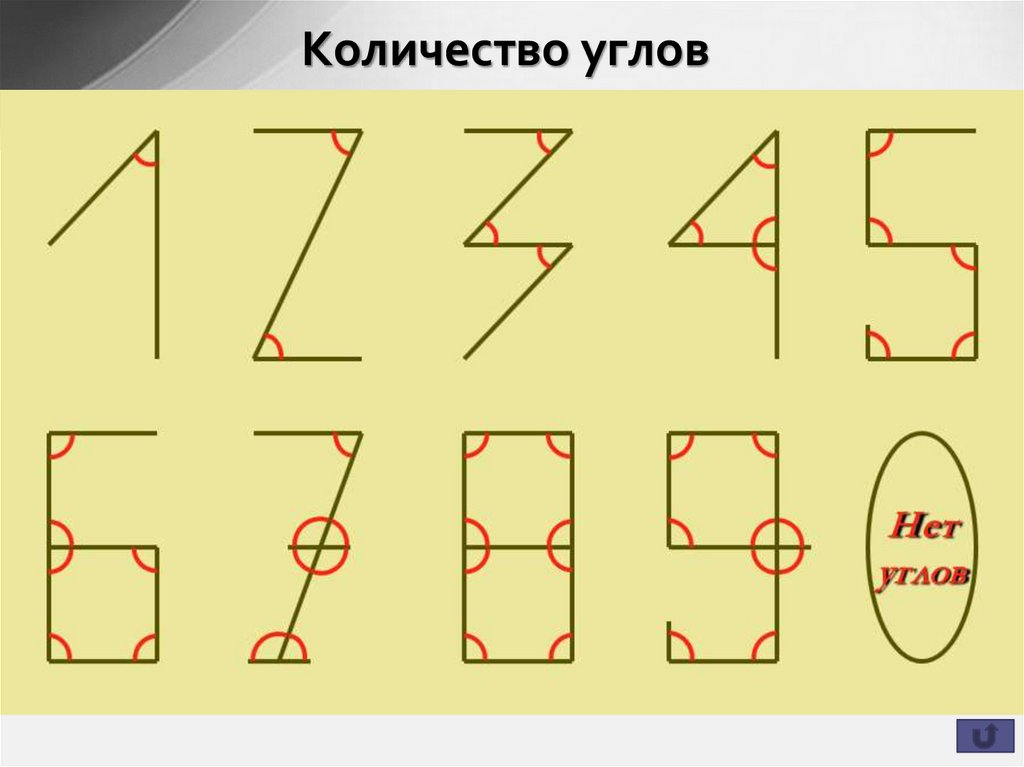
Количество углов

32. Цифры «губар» мавританских государств

33. Предположение А.С.Пушкина

34. Количество углов