Системы счисления с древних времён до современного мира

1. Системы счисления с древних времён до современного мира, их применение

Ёч Станислав Константинович
6 класс МОУ «Лицей»

2.

За долгую историю
развития
человеческого
общества
использовались
различные способы
счёта и записи чисел.
Целью настоящей
работы является
исследование способов
записи чисел,
применяемых в
древности, их влияние
на современную науку
и культуру, а также
изучение современных
систем счисления.
Задачей настоящей
работы является обзор
способов записи чисел
и иллюстрация
математической
культуры с древних
времен на примере
решения задач.

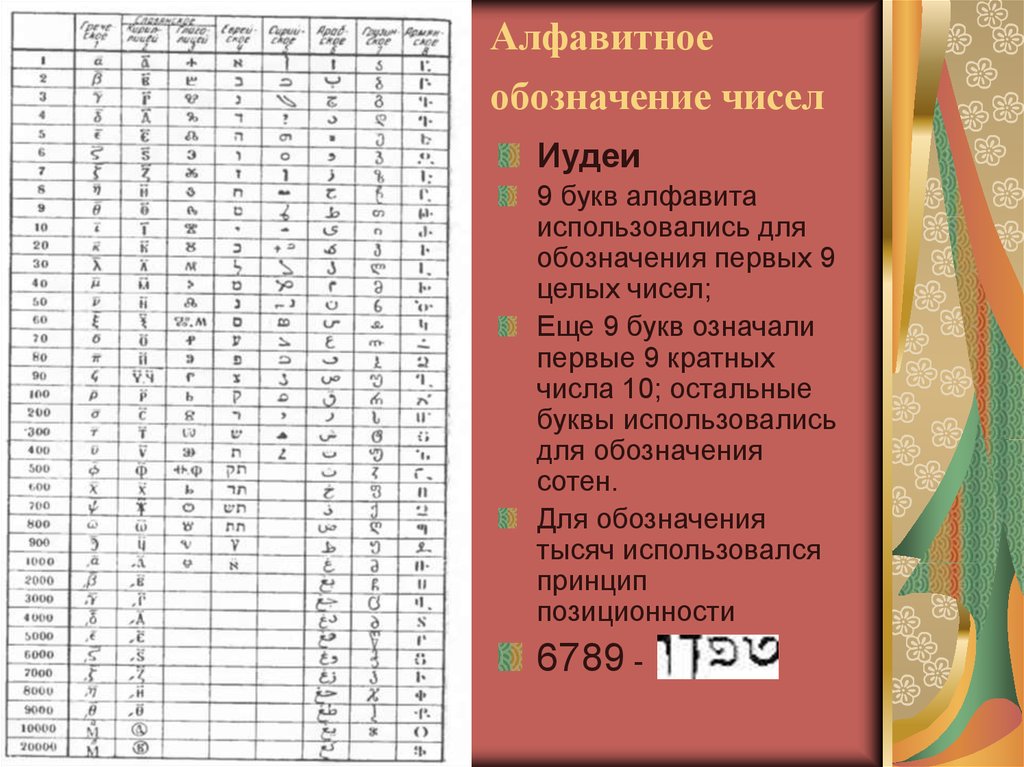
3. Алфавитное обозначение чисел

Иудеи
9 букв алфавита
использовались для
обозначения первых 9
целых чисел;
Еще 9 букв означали
первые 9 кратных
числа 10; остальные
буквы использовались
для обозначения
сотен.
Для обозначения
тысяч использовался
принцип
позиционности
6789 -

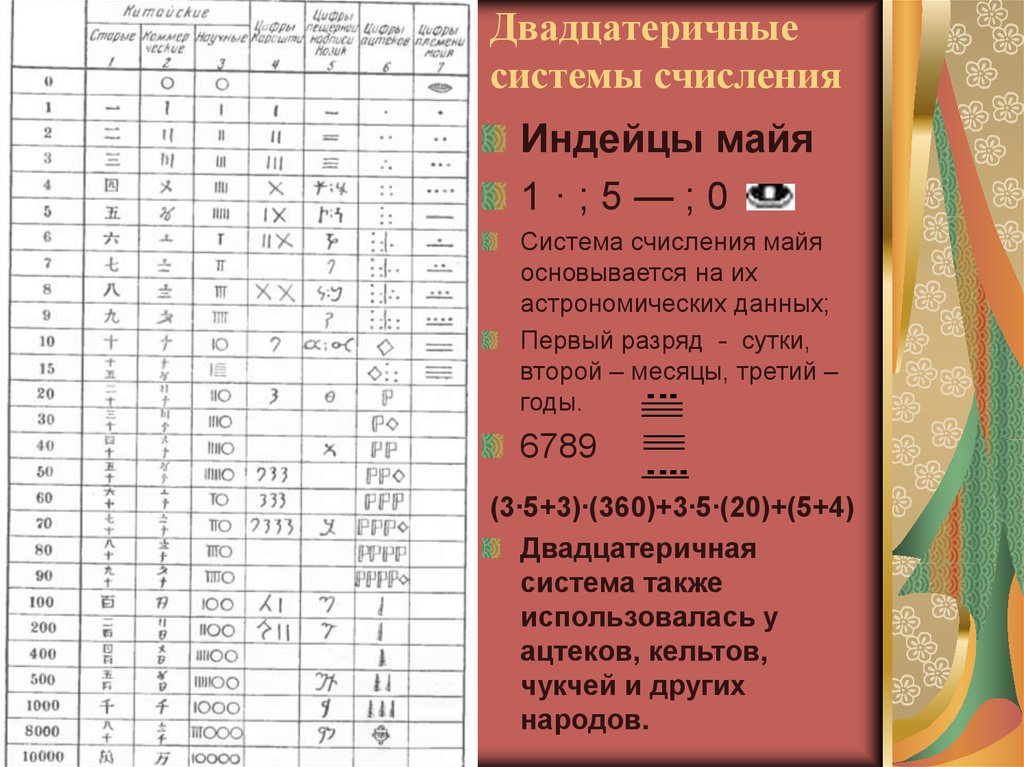
4. Двадцатеричные системы счисления

Индейцы майя
1·;5—;0
Система счисления майя
основывается на их
астрономических данных;
Первый разряд - сутки,
второй – месяцы, третий –
годы.
6789
(3∙5+3)∙(360)+3∙5∙(20)+(5+4)
Двадцатеричная
система также
использовалась у
ацтеков, кельтов,
чукчей и других
народов.

5. Древний Китай

II в. до н.э. - «Трактат об измерительном шесте» и
«Математика в девяти книгах»
Счёт палочками
Счётная доска «суань»
Принцип
позиционности
1 | ; 6 T ; 10 — ; 60
Т
6789
Отрицательные числа
– «фу»;
Положительные числа
– «чжэн»
Иероглифическая
система
Десятичная,
мультипликативная;
Для обозначения первых
9 чисел использовалось 9
знаков и 11 символов для
обозначения степеней
числа 10.
6789
(6×1000 + 7×100 + 8×10 + 9)
Дроби. Половина - «бань», треть – «шао бань», две
трети – «тай бань». III в. н.э. – десятичные дроби.
Методы «тянь-юань» (небесный элемент); «фан чэн»

6. Индия

Цифры карошти
Цифры брахми
Большинство трактатов
написано на санскрите
(алфавит «деванагари»)
6789
Система десятичная,
позиционная, цифровая.
Предшественник
современной.
1021 записывалось словами «Луна – дыра – крылья – Луна»;
«шунья» (пустое) – по арабски «сыфр»
Положительные числа - «дхана» или «сва», отрицательные – «рина» или «кщайя».
С сер. II тыс. до н.э. – дроби: ардха (1/2), пада (1/4), три-пада (3/4) и кала (1/16) с
системой записи обыкновенных дробей с числителем, расположенным над знаменателем.
Разработаны правила основных арифметических действий.
Индийские математики и астрономы Ариабхата (V-VI вв.), Брахмагупта (VII в.), Магавира
(IX в.), Шридхара (IX-X вв.), Бхаскара (XII в.), Нилаканта (XV-XVI вв.)

7. Арабские страны

Буквенная нумерация - «абджад» и «джумал»
Книги Мухаммеда Бен Муса аль-Хорезми (878-ок.850) «Об
индийском счёте», «Китар аль-джебр валь мукабала»
(«Книга о восстановлении и противопоставлении»)
Индийские цифры:
На востоке: 6789
На западе: Гобари («Песчаный абак») 6789
О влиянии науки арабских стран на науку Европы говорят
термины: арабские цифры, алгебра, алгоритм, цифра,
корень, синус.
Учёные, которые обогатили науку: Мухаммед аль-Хорезми,
астрономы ал-Фергани, ал-Тюрки и Абдуль Хасан, ал-Сагани,
ал-Ходженди и ал-Джаухари, ал-Беруни из Хорезма и идн-Сина
из Бухары (IX-X вв.), известный математик и поэт Омар Хайям
(XI в.) и ал-Каши – директора обсерватории правителя Улугбека
(XV в.).

8. Славяне

Славянская нумерация восходит к греческой
буквенной нумерации
При Петре I были введены арабские цифры
6789
22 ,
«како», «веди»
156 ,
«рцы», «наш»,
«зело»
«земля»,
«веди»
«твердо»,
«како», «аз»
7002 ,
320001 .

9. Западная Европа

В Европе использовались римские
цифры, система арифметики при
помощи абака.
В 12 в. переведён трактат «Об
индийских числах» Аль-Хорезми
С XVI в. индо-арабская система
стала использоваться
применительно к дробям.
Симон Стевин - трактат De Thiende (Десятина); 6789
С XVII в. цифры приняли практически современный вид
В эпоху Возрождения окончательно была
введена позиционная десятичная
арифметика.
Была создана арифметическая и
алгебраическая символика. Введены были
дробные и отрицательные показатели и
числа; успешно найдено решение в
радикалах уравнений 3 и 4 степеней. Были
формально введены мнимые числа.
Математика становилась средством
решения не только практических задач.
Долгий период изучения постоянных
величин подходил к завершению. Были
созданы условия для возникновения теории
переменных величин, аналитической
геометрии, дифференциального и
интегрального исчислений.

10. Современные системы счисления

Десятичная система
Двоичная система
6789=6·103+7·102+8·101+9·100
6789 = (1101010000101)2
Таблица сложения и
умножения
Десятичная
система
Двоичная
система
Десятичная
система
Двоичная
система
0
0
9
1001
0+0=1
0х0=0
1
1
10
1010
0+1=1
0х1=0
2
10
11
1011
1+0=1
1х0=0
3
11
12
1100
1+1=10
1х1=1
4
100
13
1101
5
101
14
1110
6
110
15
1111
7
111
16
10000
8
1000
Двоичная система
используется в
вычислительной технике;
в телеграфии;
в кодировании;
в теоретических
исследованиях.

11. Восьмеричная и двенадцатеричная системы счисления

6789 = (15205)8 =
1∙84+5∙83+2∙82+5
(765,43)8
7(82) + 6(81) + 5(80) +
+4(8–1) + 3(8–2) =
501
6789=(3 e 1 9)12
=3∙123+11∙122+1∙12+9
(765,43)12
7(122) + 6(121) + 5(120) +
35
64
На американских фондовых
биржах дроби обычно
выражают в восьмых долях.
+ 4(12–1) + 3(12–2) = 1085
17
48
Используется в
традиционной системе мер
(в английской и
американской);
связана с календарем и
временем.

12. Троичная система Об одном замечательном свойстве троичной системы.

6789=(100022110)3
Троичная система является самой экономичной из
позиционных систем счислений по запасу чисел, которые
можно записать в данной системе с помощью
определенного количества знаков.
С помощью 60 знаков можно записать:
В двоичной системе 230 чисел; в троичной – 320; в
четверичной – 415; и т.д. В десятичной системе – 106; в
шестидесятеричной - 60 чисел.
320>230=415>512>610>106 > 125 > 154 > 203 > 302 > 60
Троичная система оказалась самой экономичной. Двоичная
и равносильная четверичная системы уступают троичной,
но превосходят все остальные системы.
Этот вывод не связан с количеством знаков. В общем
случае результат будет тем же. Существует строгое
математическое доказательство этого факта.

13. Двоичную и троичную систему счисления можно использовать для решения ряда математических задач.

Для взвешивания любого числа граммов песка от 1 г до n г за одно
взвешивание, достаточно иметь гири 1 г, 2 г, 4 г, ..., 2m г, где 2m≤n<2m+1,
и меньшего числа гирь недостаточно, если песок лежит на одной чашке
весов, а гири разрешается ставить на вторую чашку.
Если разрешить класть гири на обе чашки весов, то оптимальной будет система из гирек
с массами, образованными степенями тройки (1, 3, 9, 27…). Для того чтобы взвесить груз
в n г, надо представить число n в виде суммы a0+3a1+9a2+27a3, где ai=0, ±1 (i=0, 1, 2, 3).
Тогда для его взвешивания достаточно на чашку вместе с грузом положить все гири,
массы которых входят в эту сумму со знаком минус, а на противоположную чашку
положить все гири, массы которых входят в эту сумму со знаком плюс.
Этой задачей интересовался Д. И. Менделеев в бытность свою председателем
Российской палаты мер и весов. Частный случай этой задачи был опубликован в книге
Баше де Мезириака в XVII веке, а ранее был известен Фибоначчи.
Задача. 12 монет. Из двенадцати монет одиннадцать настоящих, а одна
фальшивая (она отличается по весу от настоящей, но не известно, в
какую сторону). Требуется за три взвешивания на двухчашечных весах
без гирь найти фальшивую монету и выяснить, легче она или тяжелее
настоящей.
Решение. Пронумеруем монеты: присвоим им номера 001, 010, 011, 012, 112, 120, 121,
122, 200, 201, 202, 220. Для 1 взвешивания положим на одну чашу весов те монеты, у
которых старший разряд равен 0 (то есть 001, 010, 011, 012), а на другую - те монеты, у
которых он равен 2 (200, 201, 202, 220). Если перетянет чашка с «0», запишем 0. Если
перетянет «2» — запишем 2. Если чаши весов останутся в равновесии — запишем 1. Для
2 взвешивания на одну чашу выложим монеты 001, 200, 201, 202 (то есть все те монеты,
у которых второй разряд равен 0), а на другую — 120, 121, 122, 220 (то есть те монеты, у
которых средний разряд равен 2). Запишем результат взвешивания. 3 взвешиванием
сравниваем 010, 020, 200, 220 с 012, 112, 122, 202 (соответственно, нули и двойки в
младшем разряде) и записываем третью цифру. Мы получили 3 цифры —трехзначное
число. Далее определяем фальшивую монету так: Если это число совпадает с номером
какой-то монеты, то эта монета фальшивая и тяжелее остальных. Если нет, то заменим в
этом числе все нули на двойки, а все двойки на нули. После этого оно должно совпасть с
номером какой-то монеты. Эта монета фальшивая и легче остальных.

14.

Страна
Способ записи
Иудея
Древнееврейская
Алфавитная
Племя
индейцев
мая
Позиционная с
использованием ноля.
Двадцатеричная, с
промежуточным
основанием 5.
Единицей третьего разряда являлось число 360.
Основывалась на астрономических данных.
Двадцатеричные системы счисления также
существовали у кельтов и др. народов.
Китай
Палочками. Десятичная,
позиционная с
промежуточным
основанием 5.
Использовалась для счета на счетной доске. Со II
в. до н.э. появились отрицательные числа.
Иероглифическая.
Десятичная.
Мультипликативный принцип. В Китае
использовались дроби. Разработаны правила
операций с отрицательными числами и дробями.
Индия
Деванагари. Десятичная,
цифровая, позиционная.
Является предшественником современной
десятичной системы счисления. В Индии
разработаны основные правила арифметических
действий.
Аравия
Алфавитная.
Буквенная нумерация
Гобари. Десятичная,
позиционная.
Заимствована из Индии. Была взята за основу в
Европе.
Славянская.
Алфавитная.
Заимствована у греков (ионийская система
счисления)
Русь
Особенности записи чисел.
Применение в настоящее время

15. Современные системы счисления

Способ записи
Особенности записи чисел.
Применение в настоящее
время
Современная десятичная
Используется повсеместно.
Позиционная, с основанием 10
Позиционная, с основанием 2
Используется в вычислительной
технике
Восьмеричная
Применяется в финансовом мире
Двоичная
Позиционная, с основанием 8
Двенадцатеричная
Позиционная, с основанием 12
Троичная
Позиционная, с основанием 3
Используется в традиционной
системе мер (в Английской и
Американской), связана с
календарем и временем.
Экономичная система. Можно
применять для решения задач.

16.

В работе исследованы различные способы записи чисел
с древних времён и до наших дней. Многие из них
используются в современной математике.
Эволюция способов записи чисел проходила много
этапов. Менялись основания систем счислений,
принципы записи, форма цифр или иероглифов.
Математика в Древнем Китае оказала большое влияние
на математическую науку в Древней Индии, странах Азии
и Востока. Однако многие открытия китайских учёных
стали известны в Европе уже после того, как европейцы
пришли к ним самостоятельно.
Современные арабские цифры – набор из 10 знаков используются ныне практически во всем мире для
записи чисел в десятичной системе счисления. Эта
система счисления является позиционной. Арабские
цифры происходят от индийских символов для записи
чисел. Многие достижения индийских учёных
значительно повлияли на развитие науки в арабских
странах.
Математики арабских стран впитывали знания ученых со
всего мира и распространяли их дальше. Изучение
учеными Европы науки стран ислама позволило начать
строить европейскую науку на прочном фундаменте и не
повторять заново весь пройденный их
предшественниками путь.

17.

Современные системы счислений основаны
на принципах позиционности, впервые
примененных более 4 тысяч лет назад.
Использование десятичной системы также
уходит глубоко в древность.
Учёные древности достигли огромных
успехов в математике, научились решать
сложные задачи. Влияние достижений и
открытий Древнего мира на современную
науку очень велико.