Похожие презентации:
Производная функции
1. Производная функции
y f ( x)f ( x0 )
M0
x0
Сформулируем определение производной функции y=f(x) в точке
M 0 x0 , f ( x0 )
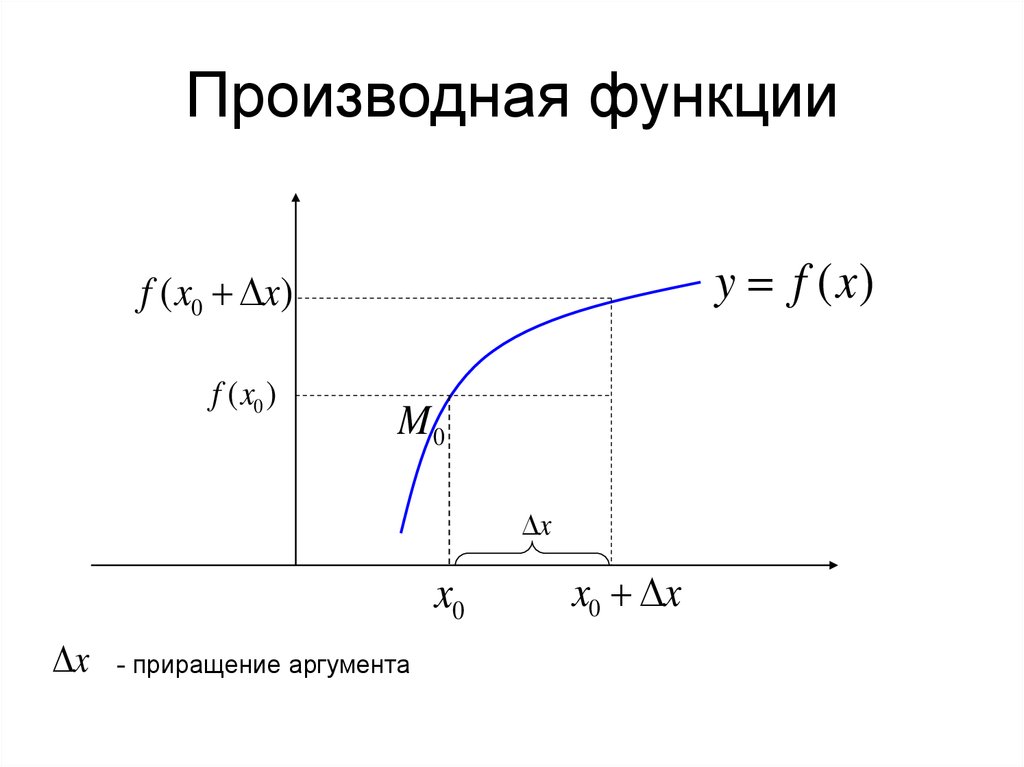
2. Производная функции
y f ( x)f ( x0 x)
f ( x0 )
M0
x
x0
x
- приращение аргумента
x0 x
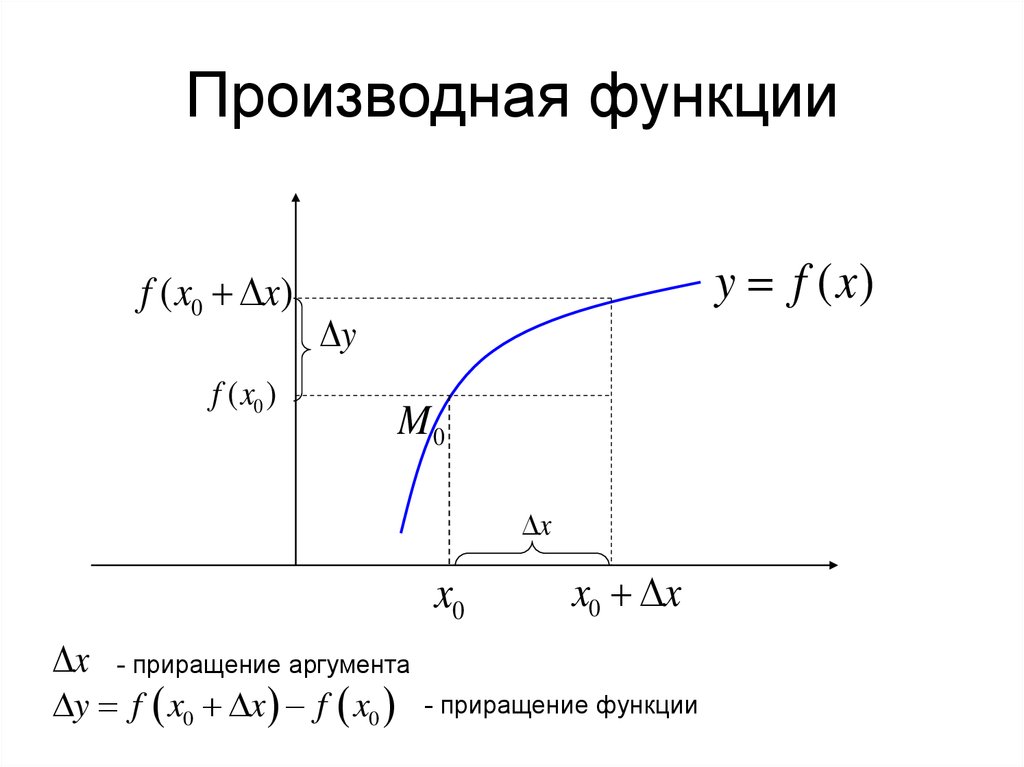
3. Производная функции
f ( x0 x)y f ( x)
y
f ( x0 )
M0
x
x0
x
x0 x
- приращение аргумента
y f x0 x f x0
- приращение функции
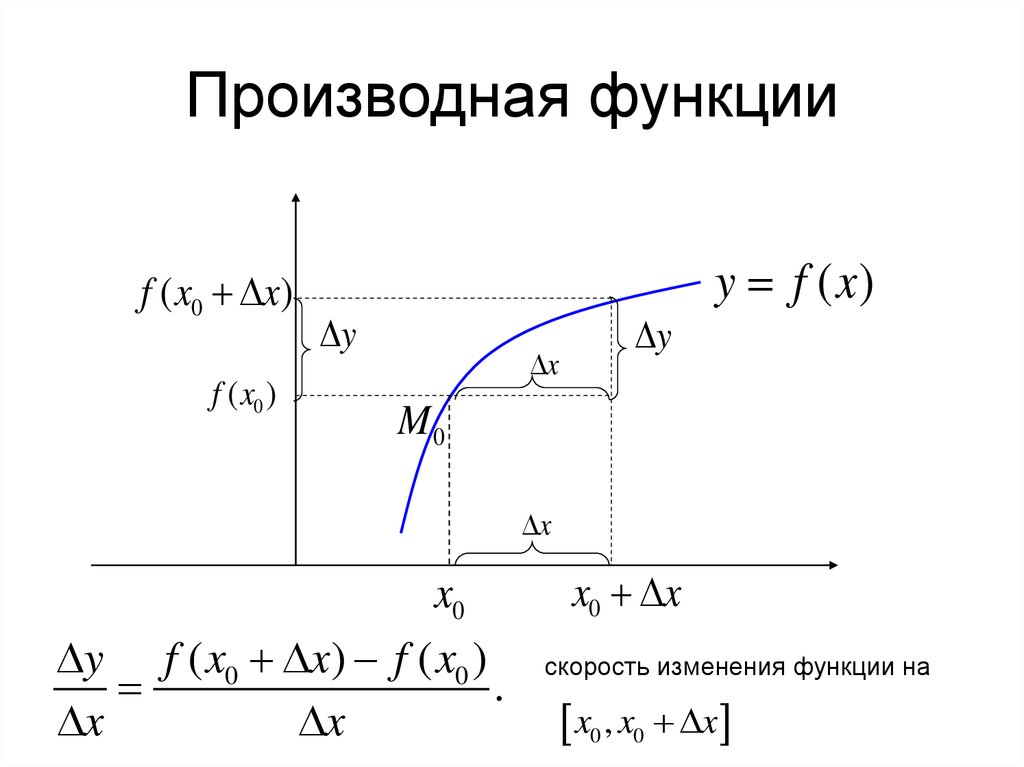
4. Производная функции
f ( x0 x)f ( x0 )
y f ( x)
y
x
y
M0
x
x0
y f ( x0 x) f ( x0 )
.
x
x
x0 x
скорость изменения функции на
x0 , x0 x
5. Производная функции
Опр. Производной функции y=f(x) в точке x0 называется предел отношения приращения функциик приращению аргумента при стремлении последнего к 0 (если этот предел существует).
y
f ( x0 x) f ( x0 )
f ( x0 ) lim
lim
.
x 0 x
x 0
x
dy
Обозначения для производной: f ( x), y ,
dx
6. Что показывает производная?
y f ( x0 x) f ( x0 )f ( x0 )
.
x
x
при малых
Если
x
x 1 , то
f ( x0 ) f ( x0 1) f ( x0 )
Производная приближенно показывает на сколько
изменится функция, если аргумент x увеличится на
1 единицу (абсолютная скорость роста функции).
7. Правила дифференцирования
1. Производная постоянной равна 0.Ñ 0
8. Правила дифференцирования
2. Производная суммы двух или нескольких функций равнасумме их производных
( f g ) f g
9. Правила дифференцирования
3.( f g ) f g g f
10. Правила дифференцирования
3.( f g ) f g g f
Следствие Постоянный множитель можно выносить за знак производной.
(c f ) c f
11. Правила дифференцирования
4. Если g(x)≠0, тоg f
f
fg
g
2
g
12. Производные основных элементарных функций
1. Логарифмическая функция.1
y log a x y
x ln a
y ln x
1
y
x
13. Производные основных элементарных функций
2. Показательная функция.y a
x
y e
x
y a ln a
x
y e
x
14. Производные основных элементарных функций
3. Степенная функция.y x
n
y n x
n 1
15. Производные основных элементарных функций
4. Тригонометрические функции.y sin x
y cos x
16. Производные основных элементарных функций
4. Тригонометрические функции.y cos x
y sin x
17. Производные основных элементарных функций
4. Тригонометрические функции.y tg x
1
y
2
cos x
18. Производные основных элементарных функций
4. Тригонометрические функции.y ctg x
1
y
2
sin x
19.
5. Обратные тригонометрические функции.y arcsin x
y
y arccos x
y
y arc tg x
y arc ctg x
1
1 x
1
2
1 x
1
y
2
1 x
1
y
2
1 x
2
20. Производная сложной функции
Теорема. Пусть h(x)=g(f(x)) – сложнаяфункция. Тогда
h ( x) g f ( x) f ( x)
21. Производные высших порядков
f ( x)называется производной 1-го порядка.
f ( x) f ( x)
- производная 2-го порядка.
22. Производные высших порядков
f ( x)называется производной 1-го порядка.
f ( x) f ( x)
- производная 2-го порядка.
f ( x) f ( x)
- производная 3-го порядка.
23. Производные высших порядков
f ( x)называется производной 1-го порядка.
f ( x) f ( x)
- производная 2-го порядка.
f ( x) f ( x)
- производная 3-го порядка.
f
(4)
( x) f ( x) - производная 4-го порядка.
24. Производные высших порядков
f ( x)называется производной 1-го порядка.
f ( x) f ( x)
- производная 2-го порядка.
f ( x) f ( x)
- производная 3-го порядка.
f
(4)
( x) f ( x) - производная 4-го порядка.
………………………………………………………..……..
f
(n)
( x) f
( n 1)
( x)
- производная n-го
порядка.














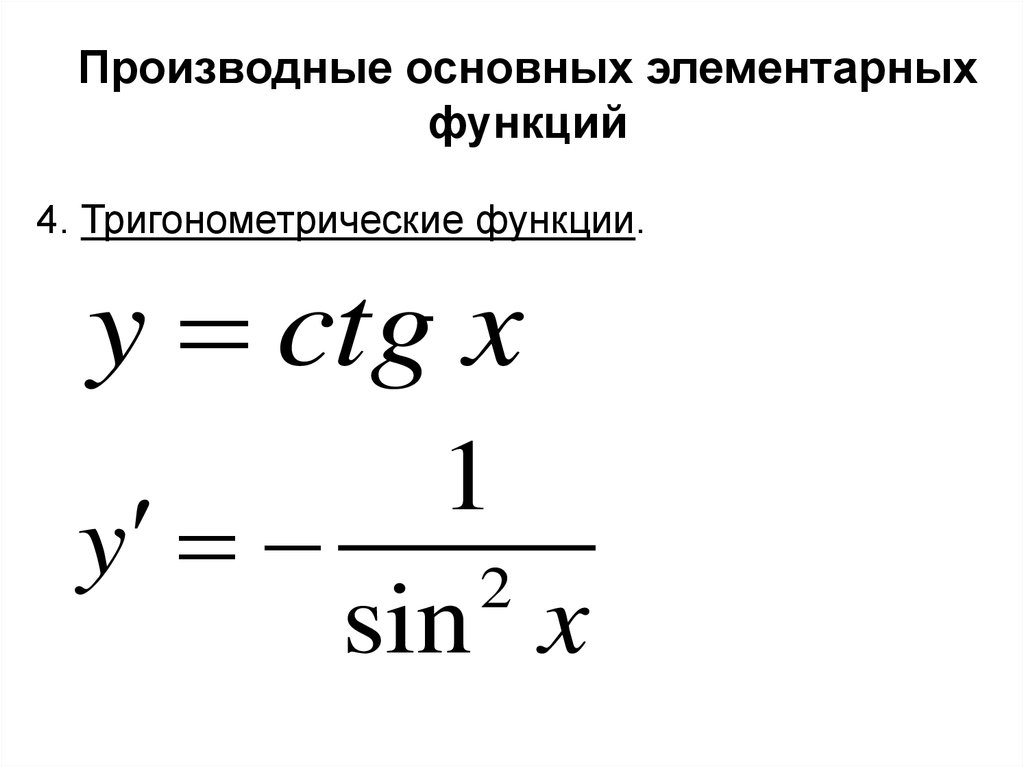






 Математика
Математика








