Похожие презентации:
Сфера и шар
1.
СФЕРА2.
Сфера и шарСферой называется поверхность, состо
ящая из всех точек
пространства, расположенных на
данном расстоянии от данной точки.
Данная точка называется центром
сферы (точка О на рис.), а данное
расстояние – радиусом сферы.
Отрезок, соединяющий две точки
сферы и проходящий через ее центр,
называется диаметром сферы. Тело,
ограниченное сферой, называется
шаром. Центр, радиус и диаметр сферы
называются также центром, радиусом и
диаметром шара.
3.
Уравнение сферыЕсли точка М лежит на данной
сфере, то MC=R, или MC², т.е.
координаты точки М удовлетворяют
уравнению
(х-х0)² + (y-y0)² + (z-z0)² = R²
(1)
Если же точка М(x;y;z) не лежит на
данной сфере, то MC² ≠ R², т.е.
координаты точки М не
удовлетворяют уравнению (1).
Следовательно, в прямоугольной
системе координат уравнение сферы
радиуса R с центром С(x0;y0;z0) имеет
вид
(х-х0)² + (y-y0)² + (z-z0)² = R² .
4.
Взаимное расположение сферыи плоскости
Если расстояние от
центра сферы до
плоскости меньше
радиуса сферы, то
сечение сферы
плоскостью есть
окружность.
Сечение шара
плоскостью есть круг.
Если расстояние от
центра сферы до
плоскости равно
радиусу сферы, то
сфера и плоскость
имеют только одну
общую точку.
Если расстояние от
центра сферы до
плоскости больше
радиуса сферы, то
сфер аи плоскость не
имеют общих точек.
5.
Касательная плоскость к сфереПлоскость, имеющая со сферой только
одну общую точку, называется
касательно плоскостью к сфере, а их
общая точка называется точкой касания
плоскости и сферы.
Теорема
Радиус сферы, проведенный в точку
касания сферы и плоскости,
перпендикулярен к касательной
плоскости.
Теорема (обратная теорема)
Если радиус сферы перпендикулярен к
плоскости , проходящей через его конец,
лежащий на сфере, то эта плоскость
является касательной к сфере.
6.
Площадь сферыМногогранник называется описанным около
сферы (шара), если сфера касается всех его
граней. При этом сфера называется
вписанной в многогранник. На рисунках
изображены описанные около сферы
тетраэдр и куб.
За площадь сферы примем предел
последовательности площадей поверхностей
этих многогранников; и получим следующую
формулу для вычисления площади сферы
радиуса R:
S=4πR².
7.
Взаимное расположение сферыи прямой
Окружность L и
прямая а не
имеют общих
точек, поэтому
сфера и прямая
а также не
имеют общих
точек.
Окружность L и
прямая а имеют
ровно одну общую
точку, поэтому
сфера и прямая а
также имеют
ровно одну общую
точку .
Окружность L и
прямая а имеют
ровно две общие
точки , поэтому
сфера и прямая а
также имеют ровно
две общие точки.
8.
Прямая, имеющая со сферой ровно однуобщую точку называется касательной к
сфере, а общая точка – точкой касания
прямой и сферы.
Радиус сферы проведенный в точку касания
сфер и прямой, перпендикулярен к этой
прямой , проходящей через его конец,
лежащий на сфере, то эта прямая является
касательной к сфере.
Отрезки касательных к сфере, проведенный
из одной точки, равны и составляют равные
углы с прямой , проходящей через эту точку
и центр сферы.
9.
Сфера, вписанная вцилиндрическую поверхность
Сфера вписана в цилиндрическую
поверхность, если она касается всех ее
образующих.
Существует сфера, касающаяся
плоскости α и цилиндрической
поверхности.
10.
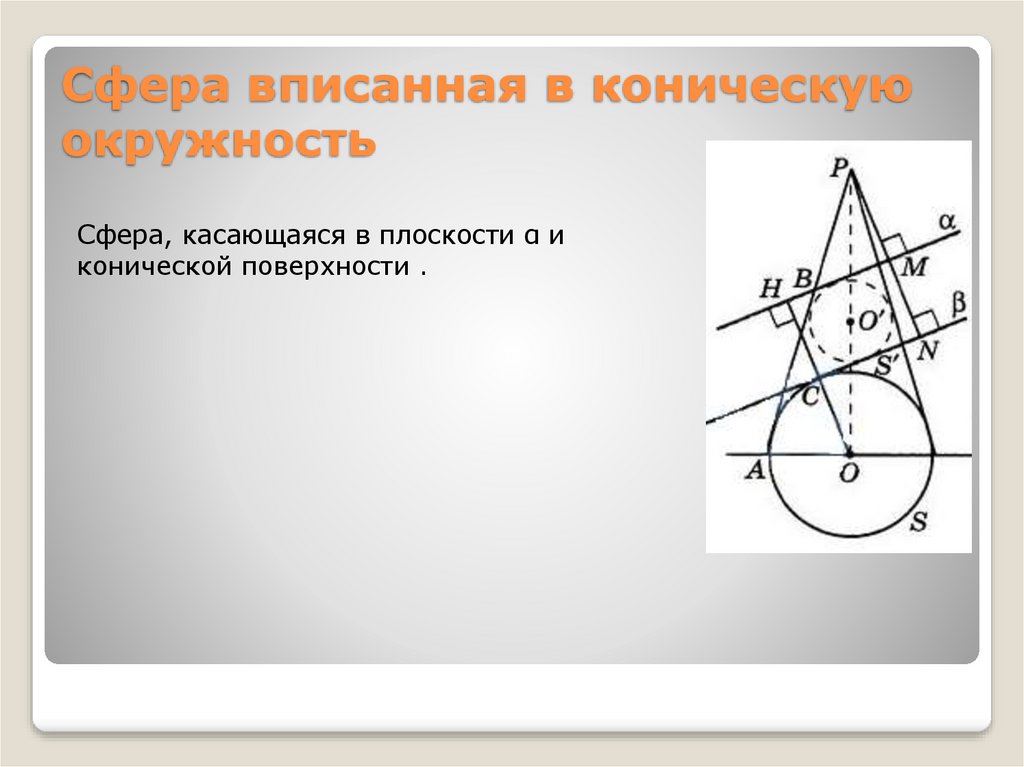
Сфера вписанная в коническуюокружность
Сфера, касающаяся в плоскости α и
конической поверхности .
11.
Сечения цилиндрическойповерхности
Отрезки M-F1 и MM1 являются отрезками
касательных, проведенными из точки М к сфере
S1 поэтому
MF1 =MM1.
Отрезки MF2 и ММ2, будучи отрезками
касательных, проведенными из точки М к сфере
S2, равны:
MF2 =MM2.
Таким образом,
MF1 + MF2 =MM1+ММ2 .
Сечением цилиндрической поверхностью α
является эллипс.
12.
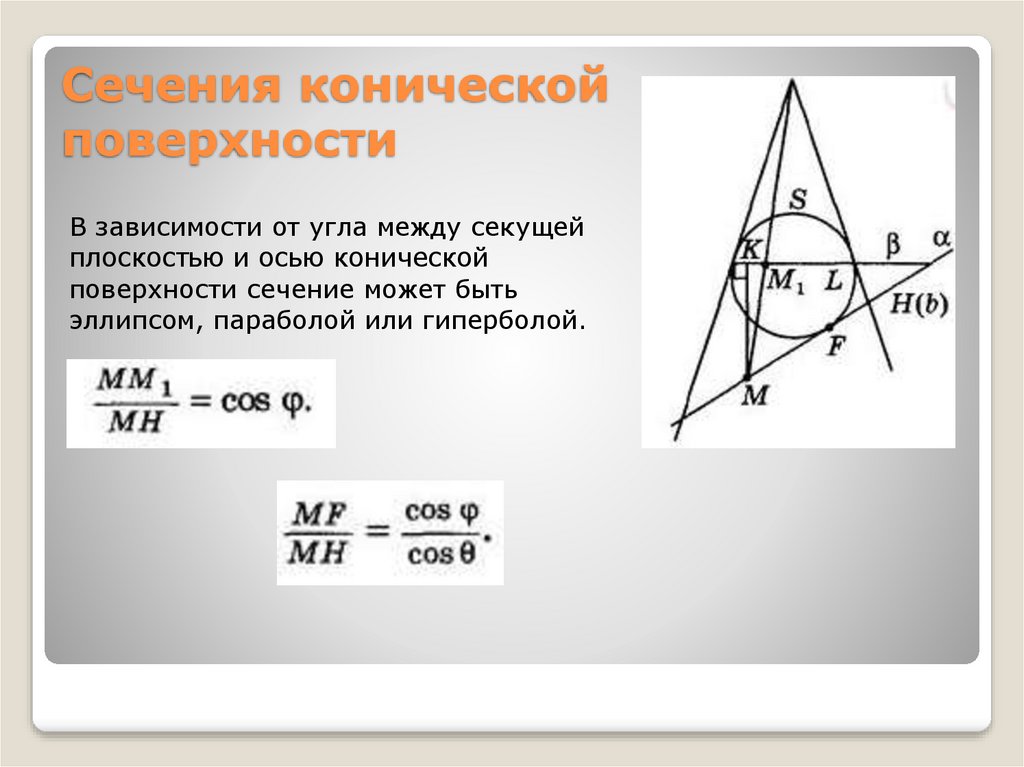
Сечения коническойповерхности
В зависимости от угла между секущей
плоскостью и осью конической
поверхности сечение может быть
эллипсом, параболой или гиперболой.










 Математика
Математика








