Математика ғылымының бұлақ-бастаулары

1.

№ 1 дәріс
Кіріспе. Математика ғылымының
бұлақ-бастаулары

2.

Дәріс жоспары:
1
Курстың объектісі, пәні және оны оқытудың мақсат-міндеттері.
2
Курстың басқа оқу пәндерімен байланысы.
3
Математиканың даму тарихының жалпы сипаттамасы.
4
Математикалық білімдердің пайда болуы мен жинақталуы

3.

1. Курстың объектісі, пәні және оны оқытудың мақсат-міндеттері.
Курстың
объектісі:
Курстың
пәні:
• тарихи-математикалық білім 5B010900 – Математика мамандығы
бойынша ҚР мемлекеттік стандарты талаптарына сәйкес
бакалаврдың жоғары кәсіби педагогикалық білімінің құрамдасы
ретінде
• бакалаврдың математика ғылымының даму тарихынан 5B010900
– Математика мамандығы бойынша ҚР мемлекеттік стандарты
талаптарына сәйкес білім, білік және дағдыларын қалыптастыру
барысы.
Курстың
мақсаты:
• білім алушыларға математика ғылымының дамуы туралы түсінік
беру, бұл тәжірибелерді меңгеру олардың болашақтағы кәсіби
міндеттерін орындауға көмектесетіндігін ашып көрсету.
Курстың
негізгі
міндеті:
математиканың қалыптасуы мен даму динамикасы туралы білімдерді
тереңдете түсу, өткен кезеңдердегі және қазіргі күнгі математика
ғылымының көрнекті өкілдерінің ғылыми идеяларымен танысу.

4.

«Математика тарихы» пәні бойынша жүргізілетін сабақтар
ДӘРІС
сабақтары
• білім алушылардың басты назары сәйкес кезеңдегі математика
ғылымының даму барысына сипаттама беруге және соның
барысында байқалатын жалпы заңдылықтарды ашып көрсетуге
аударылады
ПРАКТИКАЛЫҚ
сабақтар
• әралуан сипаттағы әдістемелік тапсырмалар орындалады,
тарихи-математикалық әдебиет пен оны шығармашылық
тұрғыда пайдалану бағытындағы жұмыстар жүргізіледі
СОӨЖ
(студенттің
оқытушы
жетекшілігімен
орындайтын
өздік жұмысы)
• білім
алушыларға
ғылымының
дамуы туралы
беру,
курстың
кейбірматематика
мәселелері
білім алушыларға
өз түсінік
бетімен
бұл
тәжірибелерді меңгеру
олардың болашақтағы кәсіби міндеттерін
оқып-үйренуге
ұсынылады.
орындауға көмектесетіндігін ашып көрсету.

5.

Математика тарихы - математиканың дамуының обьективтік
заңдылықтары туралы ғылым. Ол:
1
• математиканың дамуындағы фактілер мен мағлұматтардың
байлығын ашады;
2
• математиканың практикалык мұқтаждығын және адам
әрекеттерін, басқа ғылымдардың дамуын, коғамның
әлеуметтік және таптық құрылысы мен қатынасын,
байланысын ашуға тырысады;
3
• математиканың логикалық-құрылымының тарихи
шарттылығын, оның өзгеру диалектикасын ашып
көрсетеді;
4
белгілі дәрежеде математика ғылымының даму болашағын,
перспективасын болжауға мүмкіндік береді.

6.

2. Курстың басқа оқу пәндерімен байланысы
«Математика тарихы»
мынадай оқу пәндерімен тығыз байланысты
«Математика»
«Математиканы
оқыту әдістемесі»
«Ғылым
тарихы»
«Философия
тарихы»

7.

8.

3.Математиканың даму тарихының жалпы сипаттамасы
Математика тарихын
бөліп қарастыруға болады:
шартты түрде мынадай дәуірлерге
1. Математика ғылымының
ғасырға дейінгі дәуір).
бұлақ-бастаулар
дәуірі
(IX
2. Элементар математика дәуірі (IX-XVII ғғ.).
3. Жоғары математика дәуірі (XVII-XIX ғғ.).
4. Қазіргі заманғы математика дәуірі (XIX ғасырдан бастап
қазірге дейін).

9.

I. Математика ғылымының бұлақ-бастаулар дәуірінде (IX ғ. дейінгі дәуір)
- нақты объектілер мен біртекті объектілердің жиыны ретінде сан және
геометриялық фигура ұғымдары қалыптасты;
- санау мен өлшеу мәселелері әртүрлі сандарды, ұзындықтарды, аудандар
мен көлемдерді салыстыруға мүмкіндік туғызды;
- эмпирикалық жолмен арифметикалық амалдардың қасиетттері мен
қарапайым фигуралардың аудандары мен денелердің көлемдерін өлшеудің
тәсілдері туралы білімдер жинақтала бастады.
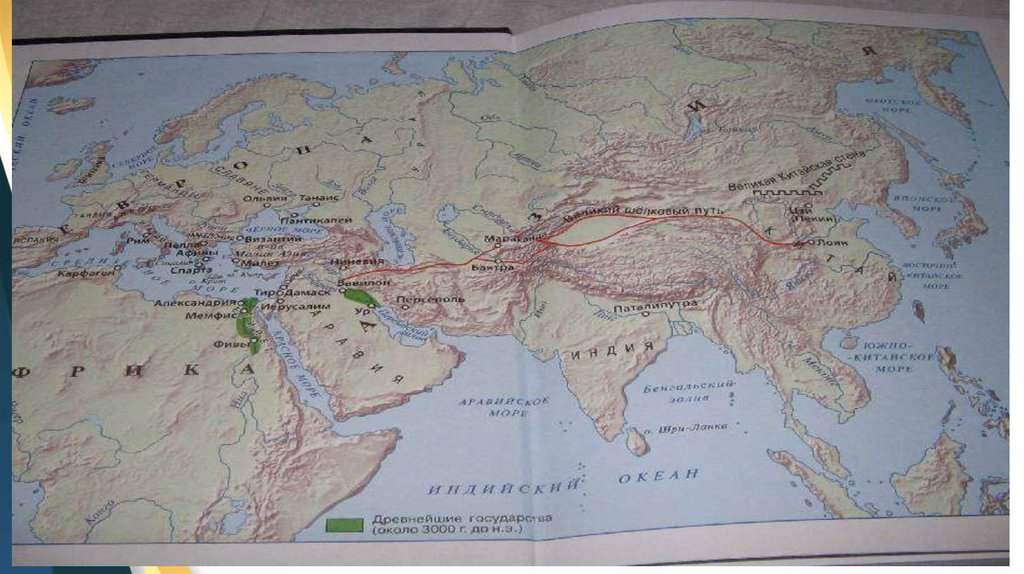
Бұл бағытта ежелгі мысырлықтар, вавилондықтар, қытайлықтар мен
үндістандықтар зор табыстарға жетті. Осы дәуірде ежелгі Грекияда
дедуктивтік математикалық жүйе пайда болды, ол бұрынғы математикалық
білімдер негізінде жаңа математикалық ақиқатқа қалай қол жеткізудің
жолдарын көрсетіп берді. Сонымен қатар геометрия ғылымының негізі
салынды.

10.

II. Элементар математика дәуірі (IX-XVII ғғ.)
- мұсылман әлемі математиктері математикадағы осыған дейінгі қол
жеткізілген жетістіктерді игере отырып, элементар математиканы жүйеге
келтіруді қолға алды;
- қазіргі заманғы арифметика мен алгебраның негіздері қаланды,
геометрия мен тригонометрияда айтарлықтай нәтижерге қол жеткізіліп,
элементар математика жүйеге келтірілді;
- мұсылмандық өркениеттің тікелей ықпалымен еуропалық математика
жанданып, алдыңғы қатарға шыға бастады;
- Қайта өрлеу дәуірінде (XV-XVI ғғ.) инженерлер, құрылысшылар,
суретшілер, әскерилер мен теңізде жүзушілер тарапынан математикаға
деген сұраныс жедел қарқынмен артты;
- ғылыми ой-пікірдің дамуы аса күрделі есептерді шешу мәселесін күн
тәртібіне қойды, бұл өз кезегінде, математиканың теориялық негіздерінің
дамуына әсер етті.

11.

III. Жоғары математика дәуірі (XVII-XIX ғғ.).
- айнымалы шамалар математикасына деген қызығушылық артты, оның
концептуалдық негізі математикалық модельдердің әлемнің идеалдық
қаңқасы болып табылатынына деген сенімнің күшеюімен сипатталады;
- математиканың басты жетістігі айнымалы шамалар арасындағы
тәуелділік пен қозғалыстың жалпы теориясының математикалық
модельдерін жасалды;
- жоғары математика ашылып, барлық жаратылыстану ғылымдары жоғары
математиканың негізінде жаңадан ашылған математикалық модельдердің
базасында қайтадан жасақтала бастады.

12.

IV. Қазіргі заманғы математика дәуірі (XIX ғ. бастап қазірге дейін)
- жоғары математиканың қолданылу аясы кеңейе түсті;
- жоғары математиканың аса маңызды салалары (дифференциалдық
теңдеулер, вариациялық есептеулер, математикалық физика теңдеулері,
векторлық анализ, ықтималдықтар теориясы, комплекс айнымалылар
функциясы теориясы, эллипстік функциялар теориясы, группалар
теориясы, дифференциалдық геометрия, евклидтік емес геометрия,
математикалық логика, сандар теориясы, нақты айнымалылар функциясы
теориясы, функциональдық анализ, анализдің сандық әдістері, т.б.)
ашылып, олар жедел қарқынмен дамыды;
- көптеген аса күрделі математикалық проблемалар өз шешімін тапты;
- математикалық есептерді шешуде компьютердің мүмкіндіктерін
пайдаланудың маңызының арта түсуіне байланысты программалау
теориясы қарқынды дами бастады.

13.

I. Математика ғылымының бұлақ-бастаулар дәуірін
(IX ғ. дейінгі дәуір) екі кезеңге бөліп қарастыруға болады:
1.Практикалық математика кезеңі (б.з.д.VI-V ғғ. дейін);
2.Теориялық математика кезеңі (б.з.д.VI-V– IX ғғ.).

14.

I. Математика ғылымының бұлақ-бастаулар дәуірінде (IX ғ. дейінгі дәуір)
мынадай математикалық білімдер қалыптасты:
1. Натурал сан ұғымы туралы түсінік пен санау жүйелері қалыптасты;
2. Есептеу мәдениеті пайда болды;
3. Есептерді шешудің ескілікті әдістері ойлап табылды;
4. Натурал сандардың қасиеттері туралы алғашқы білімдер жинақталды;
5. Шамалар және оларды өлшеу туралы түсініктердің пайда болды;
6. Бөлшек сан ұғымы туралы алғашқы түсініктер қалыптаса бастады;
7. Өлшемдес емес шамалардың ашылды;
8. Теріс сан туралы алғашқы түсініктер пайда болды;
9. Алғашқы геометриялық білім-түсініктер пайда болды;
10. Теңдеулер және оларды шешудің алғашқы тәжірибелері жасалды;
11. Теориялық-дедукциялық математиканың қалыптасуы

15.

1. Натурал сан ұғымының қалыптасуы
Натурал сан - математиканың объектілердің және
олардың бөліктерінің мөлшерлік сипаттамасын беру, оларды
өзара салыстыру және нөмірлеу үшін қолданылатын негізгі және
ежелгі ұғымы.
Натурал сан ұғымының пайда болуына түрткі болған
тарихи жағдайларды ашып көрсету өте күрделі және аса қиын
мәселе.
Сан туралы ұғымның қалыптасуы – ұзақ уақытқа
созылған, бірнеше кезеңдерді бастан кешірген және қашан
басталғандығын болжап айтудың өзі аса қиын өте ұзақ тарихи
үдеріс.

16.

Натурал сан ұғымының қалыптасу үдерісінің төмендегідей негізгі
кезеңдерін бөліп көрсетуге болады:
1. Санау өнеріне қажет болатын дерексіздіктердің пайда болу кезеңі.
2. Сезімдік санау кезеңі.
3. Жиындарды олардың элементтерінің мөлшеріне қарай салыстыру кезеңі.
4. Санау эталонын меңгеру кезеңі.
5. Топтап санау және сан есімдерді енгізу кезеңі.
6. Натурал сан қатарын игеру кезеңі.
7. Сан таңбаларын енгізу кезеңі.
8.Санау жүйелерін меңгеру кезеңі.

17.

I. Санау өнеріне қажет болатын дерексіздіктердің пайда болу кезеңі
«Натурал сандарды жаратқан құдай, ал қалған сандардың бәрін ойлап
тапқан адамдар».
Л.Кронекер (1823-1891)
Қандай да болмасын алғашқы ұғым - шындық дүниенің нақты
заттары мен құбылыстарының қасиеттері мен қатынастарының
бейнеленуі, ол адамның белсенді іс-әрекеті барысында қалыптаса
бастайды.
Еңбек пен сөйлеу барысында адамның миы мен сезім мүшелері
бірте-бірте жетіле түсті. Осының нәтижесінде адам миы санау мен
өлшеуде қажет болатын дерексіз ұғымдарды меңгеру қабілетіне ие бола
бастады.

18.

II. Сезімдік санау кезеңі.
Адам баласы заттар жиынын элементтерінің саны одан көп немесе
аз басқа жиындармен салыстыруға үйрене бастады. Санаудың бұл түрін
сезімдік санау деп атайды. Мұның кейбір ұшқындары жан-жануарлардың
әрекеттерінен де ұшырасады. Мәселен, қаз артынан өзінің
балапандарының бәрінің еріп келе жатқанын осылайша анықтайды.
Сезімдік санаудың бір түрі - түстеп түгелдеу. Алғашқы адам топтағы
заттарды түстеп түгелдеуді меңгерген. Абипон үндістері аңға шығар
алдында көп иттерін көз мөлшерімен шолып шығу арқылы қай итінің жоқ
екендігін бірден анықтап, біле алған.
Грендландия эскимостары балаларының санын білмеген, олар балаларын
да шанаға жегетін иттерін де түр-түстеріне қарап айыратын болған.
Түстеп түгелдеу әлі санды және санауды меңгере қоймаған жас
балалардың әрекетінде де аңғарылады. Жас сәби өзінің ойыншықтарын
түстеп түгендейді.

19.

III. Жиындарды элементтерінің мөлшеріне қарай салыстыру кезеңі.
Заман өте келе, сезімдік санау жеткіліксіз бола бастады. Адам
баласы өзінің қолындағы бар заттарын басқа бір заттарға ауыстырып алу
үшін бір қатарға өзінің заттарын тізіп қойып, олардың әрқайсысының
астына ауыстырып алынатын заттарды сәйкестендіріп қою арқылы
олардың мөлшерлерінің бірдей екендігін анықтай алатын болды. Мәселен,
ол төрт зат тобының мөлшерін «иттің қанша аяғы болса, сонша зат» деген
тұрғыда түсіндіруді үйренді.«екі жиын элементтері арасында өзара
бірмәнді сәйкестікті тағайындау» деп аталады.
Осы амал сан ұғымының қалыптасуында аса маңызды роль атқарды,
өйткені оның негізінде жиындарға енетін заттардың мөлшерінің бірдей
болуы немесе бірдей болмауы «тең», «артық» және «кем» ұғымдарының
қалыптасуына әкеліп соқтырды.

20.

IV. Санау эталонын меңгеру кезеңі.
Адам баласы санаудың табиғи эталондарын таңдап алуға үйрене
бастады. Мәселен, қандай да бір топта бес заттың бар екенін бір
қолынының саусақтарын көрсету арқылы білдіретін болды. Кейін келе, ол
біртіндеп санаудың жасанды эталондарын меңгеруді қолға алды. Белгілі
бір топта қанша заттың бар екенін анықтау мақсатында ұсақ тастарды,
таяқшаларды, т.с.с. қолдануды үйренді.
Жиын-эталон оған теңмөлшерлі кез келген басқа бір басқа
жиындардағы заттардың мөлшерін анықтаудың ерекше бір құралы
қызметін атқарды. Жиын-эталонның пайда болуы натурал сан ұғымының
қалыптасуында үлкен роль атқарды, себебі адам баласының санау өнерін
меңгеру мақсатындағы осы сияқты әрекеттері оның натурал сан ұғымын
барлық теңмөлшерлі жиындардың ортақ қасиеті ретінде түсіне бастауына
жол ашты.

21.

V. Топтап санау және сан есімдерді енгізу кезеңі.
Адам баласы біртіндеп сан атауларын, яғни сан есімдерді енгізуді
жүзеге асырды. Адамзаттың алғашқы қолданған сан есімдері - «бір» мен
«екі», екіден артық сандарды айыра алмағандықтан, «көп» деп айта салатын
болған. Осы қиындықты жеңу үшін адам баласы саналатын заттарды екіекіден, бес-бестен, он-оннан, жиырма-жиырмадан топтап алып, көп санды өзі
білетін аз санды пайдалану арқылы өрнектеуге тырысқан. Мысалы, Торрес
бұғазы тайпаларының сан атаулары мынадай: 1 – «урапун», 2 – «окоза», 3 –
«окоза - урапун», 4 – «окоза-окоза», 5 – «окоза- окоза-урапун», 6 – «окоза –
окоза - окоза», т.с.с.
Ацтек үндістерінде 5 саны «чику» деп аталған да осының негізінде одан
кейінгі сан атаулары мынадай: 6 – «чикуасе» [5 + 1(«се»)], 7 – «чикоме» [5 +
2(«оме»)], 9 – «чикунауи» [5 + 4(«науи»)]. Бұл мысалдар екі-екіден және
бес-бестен топтап санаудың іздерін аңғартады.

22.

VI. Натурал сан қатарын игеру кезеңі.
Топтап санауды игеру барысында топтаудың негізі болып
табылатын сандарға ерекше назар аударыла бастады. Осы сандарды негіз
етіп алып, басқа үлкенірек сандарды өрнектеу мәселесі күн тәртібіне
қойылды. Осылайша, сандардың жоғары шекарасы кеңейе келіп, натурал
сандар қатары түзіле бастады. Әрине, алғашқыда ол тым қысқа болғаны
және біртекті болып түсінілмегені белгілі. Сан туралы ұғымының онан әрі
дами түсуімен бірге сан қатары да біртіндеп ұзара түсті. Бұрын 3-тен
немесе 10-нан артық барлық сандарды сипаттап көрсетуде пайдаланылған
«көп» сөзінің мағынасы өзгерді, енді ол 100-ден, 1 000-нан, т.б. артық
сандарды білдіретін болды. Алайда, адам баласына натурал сан қатарының
шексіз болатындығы және ең үлкен санның болмайтындығы туралы
қорытынды жасау үшін әлі де болса, көптеген ғасырлар қажет еді.

23.

VII. Сан таңбаларын енгізу кезеңі.
Адам баласы өзінің күнделікті тұрмыс-тіршілігінде кездесетін
заттар тобын санаудың әрекетінен шыққан сандарды ұмытып қалмау үшін
және керек кезінде қайтадан пайдалана алу үшін оларды белгілеп қою мен
сақтаудың жолдарын іздестіре бастады. Ертеде қандай да бір санды
білдіретін таңба тік не көлденең сызықша түрінде құмның немесе сазды
жердің бетіне түсіру арқылы, ал санау нәтижелерін сақтап қою ағаштарға
немесе жануарлардың сүйегіне кертікшелер салу, жіпке түйіндер жасау
арқылы жүзеге асырылды. Бірақ бұл үлкен сандарды таңбалауда
қиындықтар туғызды. Сондықтан адам қандай да бір санды оған сәйкес
суретті салу арқылы белгілеуді ойлап тапты. Мәселен, «екі» санын екі
көздің немесе құстың екі қанатының суретін, «бес» санын бес саусақтың
суретін салу арқылы белгіледі. Мұны пиктографиялық таңба деп атайды.

24.

Біртіндеп, адам баласы сандарды кескіндейтін суреттердің салыну
жолдарын оңайлата түсуге тырысты. Осылайша, санды осындай
оңайлатылған суреттер арқылы таңбалап жазу – иероглифтік таңбалар
пайда болды. Санды арнайы иероглифтер арқылы жазып көрсету кейбір
елдерде (Қытай, Жапония, т.б.) әлі күнге дейін қолданылады.
Бірте-бірте қоғам талаптарының өсуіне және осыған орай, аса
үлкен сандарды таңбалауды жүзеге асыруға байланысты иероглифтік
таңбалар біршама қолайсыздық тудырды. Сондықтан кейбір түйінді
сандарды белгілейтін ықшамдалған, арнайы таңбалар ойлап табылып,
иератикалық таңбалар қалыптасты. Бұдан кейін иератикалық сан
таңбалары бұрынғыдан да оңайлатылып, демотикалық таңбалар келіп
шықты.
Әр халықтарда зияткерлік даму мүмкіндіктеріне байланысты әр
кезеңдерде әртүрлі нумерациялық жүйелер мен білімдер, яғни сан
таңбалары қалыптасты.

25.

VIII. Санау жүйелерін меңгеру кезеңі.
Адам баласының білімдерінің молая түсуі сан таңбаларын белгілі
бір жүйеге түсіруді талап етті. Бұл орайда, ең алдымен топтап санау
барысында қалыптасқан түйінді сандарға (екі, бес, он, он бір, он екі,
жиырма, т.с.с.) ерекше көңіл бөлінді. Әр халықтар өзіне ыңғайлы түйінді
санды таңдап алып, оны санау жүйесінің негізі ретінде қабылдады. Санау
осы түйінді санға бірді қосу, сондай-ақ осы санды екі еселеу, үш еселеу,
т.с.с. арқылы жаңа сандарды шығарып ала отырып, келесі түйінді сан
алынғанша жүргізілді. Одан кейін негізі екінші түйінді сан болатын келесі
санау жүйесі басталды, оның сандары екінші түйінді санды бірінші
түйінді санмен комбинациялау арқылы құрастырылды. Бұл сандар үшінші
санау жүйесінің негізі болатын келесі түйінді санға дейін барды, т.с.с.
Кейбір халықтарда натурал сандарды таңбалаудың мынадай жүйесі
де қолданылған: жаңа сандар түйінді саннан оған кішірек түйінді санды
қосу арқылы алынумен бірге, одан кішірек түйінді санды азайту арқылы
да алынған. Әртүрлі халықтарда санаудың жоғарыдағы сияқты әрқилы
тәсілдерінің орын алуы барысында әралуан санау жүйелері пайда болды.

26.

Демотикалық жазудан кейін әріптердің, сондай-ақ сөздерді әріптер
арқылы жазудың ойлап табылуына байланысты кейбір халықтар
сандарды жазып, таңбалауда әріптерді пайдалануды қолға алып,
алфавиттік нумерацияға көше бастады. Осының барысында әртүрлі
халықтарда сандарды таңбалаудың өзіндік алфавиттік жүйелері
жасалды. Алфавиттік нумерациялардың кейбіреулерінде (грек, славян,
т.б.) әріптердің сан таңбалары ретінде жүретіндігін көрсету үшін әрбір
әріптің үстіне «титло» деп аталатын көлденең сызық қойылатын болған.
Алфавиттік санау жүйелері ішінен мұсылман әлемінде кеңінен
таралған арабтың алфавиттік санау жүйесін ерекше атап өту керек. Ол
қазақтар арасында «Әбжәд есебі» деп аталған.

27.

«Әбжәд есебі»

28.

Мұны қазіргі әріптер мен цифрлар арқылы жазсақ, мынадай болады:
aбжд
1234
һуз
567
қ
р
ш т
100 200 300 400
хти
8 9 10
к л м н
20 30 40 50
с
х
з
500 600 700
с ғ ф с
60 70 80 90
з
з
ғ
800 900 1000
Әбжат бойынша, арифметикалық амалдарды орындауға болады.
Мұнда көбейту кестесі «Бабди бажуан» деп аталады.

29.

Санау жүйелері:
1. Позициялық емес санау жүйелері
2. Позициялық санау жүйелері .

30.

Позициялық емес санау жүйелері:
Позициялық емес санау жүйесінде қабылданған
таңбалар жиынтығынан алынған әрбір символ санның
жазылуындағы өзінің алатын орнына (позициясына)
байланыссыз бір ғана санды білдіреді.
Мысалдары:
- ежелгі мысырлықтардың санау жүйесі;
- гректердің аттикалық немесе геродиандық санау жүйесі;
- римдік санау жүйесі.

31.

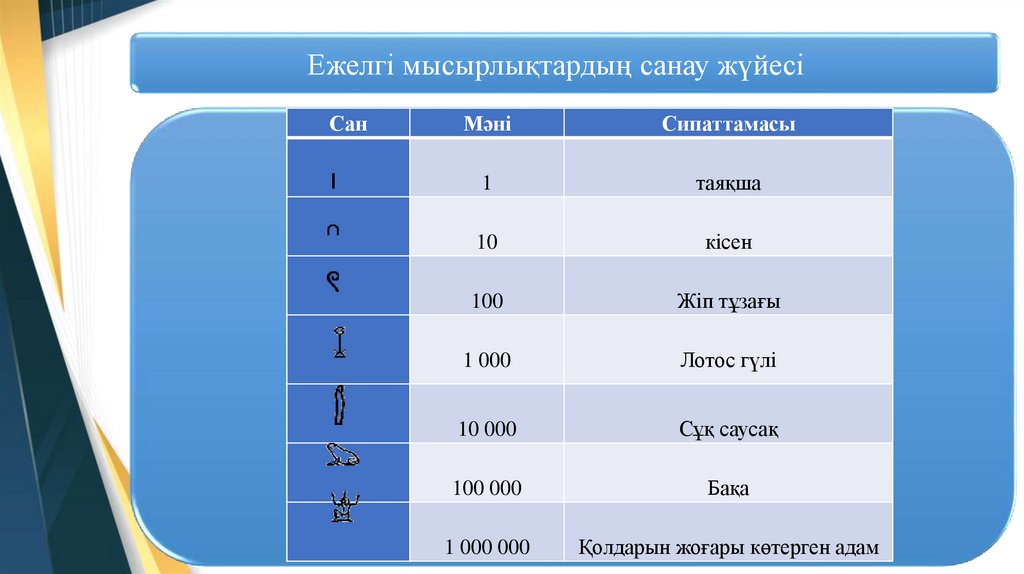
Ежелгі мысырлықтардың санау жүйесі
Сан
Мәні
Сипаттамасы
1
таяқша
10
кісен
100
Жіп тұзағы
1 000
Лотос гүлі
10 000
Сұқ саусақ
100 000
Бақа
1 000 000
Қолдарын жоғары көтерген адам

32.

33.

Райнд папирусы
Мәскеу папирусы

34.

Ежелгі мысырлықтардың математикалық білім дәрежесін айқындауға
мүмкіндік берерліктей папирустарда келтірілген есептер қысқа, догматикалык
түрде берілген, яғни есептің шарты мен талабы беріледі де шешу жолы
көрсетіледі. Ешқандай дәлелдеу, тексеру жоқ, айрықша символика жоқ, барлығы
иероглиф арқылы өрнектелген сөздер мен сөйлемдерден тұрады.Мысырлықтардан
қалған есептерді талдай келіп, оларда математикалық білім салаларының бөлінбей
арифметикалық, геометриялық, алгебралық есептердін аралас жүретінін байқауға
болады. Есептердің барлығы дерлік бірыңғай практикалық мәселелерді шешуге
арналған.

35.

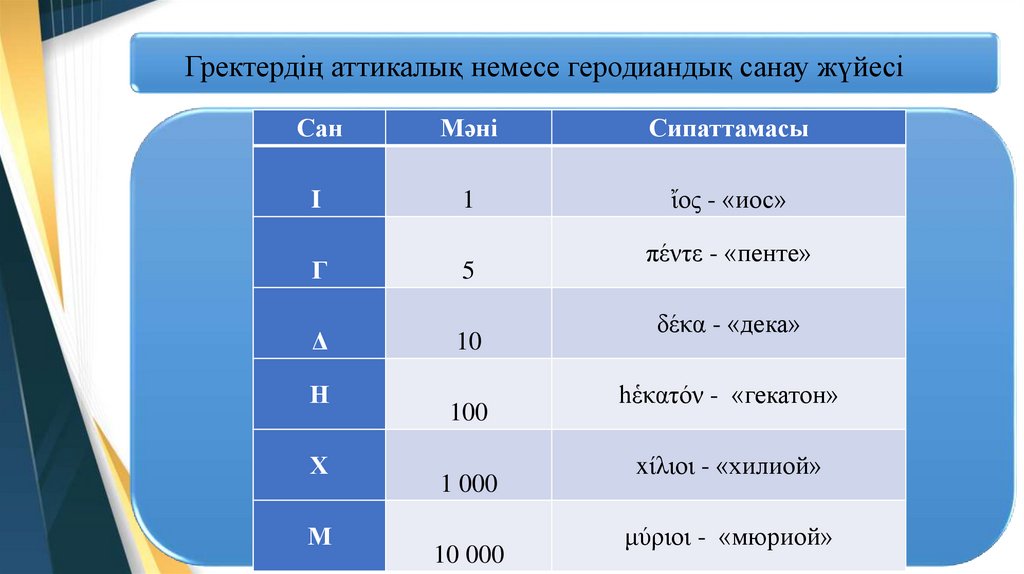
Гректердің аттикалық немесе геродиандық санау жүйесі
Сан
Мәні
Сипаттамасы
I
1
ἴος - «иос»
Г
Δ
Н
Χ
Μ
5
10
100
1 000
10 000
πέντε - «пенте»
δέκα - «дека»
һἑκατόν - «гекатон»
xίλιοι - «хилиой»
μύριοι - «мюриой»

36.

Позициялық санау жүйелері:
Позициялық санау жүйесі – бір таңба санның жазылуындағы
өзінің алатын орнына (позициясына) байланысты әртүрлі санды білдіре
алатын санау жүйесі. Ол өзінің негізімен (базисімен), яғни санды
таңбалау үшін қолданылатын символдарының санымен сипатталады.
Мәселен, қазіргі бүкіл дүние жүзінде жаппай қолданылатын ондық
санау жүйесі позициялық санау жүйесіне жатады, оның базисі онға тең
(0,1,2,3,4,5,6,7,8,9 цифрлары). Сол сияқты санды бестік санау жүйесінде
жазып көрсету үшін бес цифр жеткілікті (0,1,2,3,4 цифрлары),
сондықтан оның базисі беске тең.
Вавилондықтардың және майялардың санау жүйелері де
позициялық санау жүйесінің мысалдары болып табылады.

37.

Позициялық санау жүйелері түрлерінің ең ежелгісі вавилондықтардың алпыстық санау жүйесі.
Б.з.д. 2 000 жылдары пайда болған бұл санау жүйесі екі ғана
таңбаға негізделеді, олар: 1 мен 60 сандарының таңбасы:
және 10 мен 600 сандарының таңбасы:
Мысалы, 32 саны былай жазылады:
60-тан артық сандарды таңбалауда қайтадан 1-ден 59-ға дейінгі
сандардың таңбалары пайдаланылады, бірақ мұнда әрбір символ
бұрынғыдан 60 есе артық мәнге ие болады. Мысалы, 83 саны былай
жазылады:

38.

39.

40.

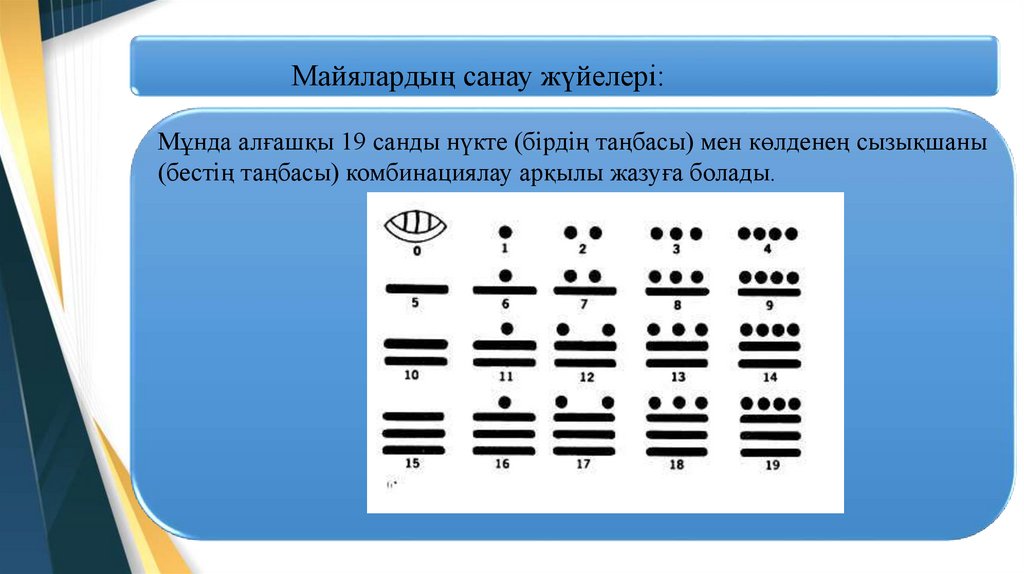
Майялардың санау жүйелері:
Мұнда алғашқы 19 санды нүкте (бірдің таңбасы) мен көлденең сызықшаны
(бестің таңбасы) комбинациялау арқылы жазуға болады.
.

41.

2. Есептеу мәдениетінің пайда болуы
Адам баласы дене еңбегін жеңілдетудің жолдарын іздестірумен
бірге, ой еңбегін, оның ішінде есептеулерді орындауды жеңілдетудің
әдістерін ойлап табуға мәжбүр болды. Алғашқыда ол онға немесе
жиырмаға дейінгі есептеу жұмыстарын орындау үшін саусақтарын немесе
барлық саусақтары мен башайларын, үлкенірек сандармен есептеулер
жүргізуде саусақтарының буындарын қолданатын болды. Кейінірек
есептеу құралы ретінде ұсақ тастарды, бақалшақтарды, дәндерді, т.с.с.
қолдануды меңгерді. Бұл орайда, әсіресе, есептеу жұмыстарында ұсақ
тастарды қолданудың тарихи роль атқарғанын атап айту керек. Ұсақ
тастарды ұдайы қолдану барысында ең алғашқы есептеу құралы – абак
ойлап табылды.

42.

АБАК
Абактың ең алғашқы түрі қақ ортасынан екіге бөлініп, құм салынған мына
сияқты жәшік түрінде болған:
Батыс Еуропада X ғасырдың соңына қарай есептеу құралы ретінде абактың
жетілдірілген нұсқасы - «Герберт абагы» қолданыла бастады. Осы кезеңде Римде кейінірек
Сильвестра II деген атпен Рим папасы қызметіне кіріскен оқымысты-монах Герберт (9401003) «Абак арқылы есептеу ережелері» атты кітап жазды. Герберт абагының пішіні 30
бағанға бөлінген құм толтырылған тақтай жәшік түрінде, оның соңғы үшеуі бөлшектерге
арналған, қалғандары 3 бағаннан 9 топқа біріктіріледі.

43.

Ежелгі есептеу құралдары:
- суаньпань;
- соробан;
- есепшот.
Орыс есепшоты деп аталып жүрген есептеу құралын ойлап тапқан орыстар
емес. XVII ғасырдағы саяхатшы Н. Витзеннің деректеріне қарағанда, орыс
есепшотының түпнұсқасын Ресейге Алтын Орданың шоқындырылған
мырзасы С.Строганов Азиядан әкелген (XIV ғ.). Ал «Орыс жазушылары
сөздіктерінің» авторы митрополит Евгений есепшотты Сібірден алғаш алып
келген Аникита Строганов (1750 ж. қайтыс болған) дейді.

44.

3. Есептерді шешудің ескілікті әдістері
Ежелгі Мысырда қолданылған:
- «Жалған жору» тәсілі.
«Үймек және оның төрттен бірі 15 болады» деп тұжырымдалатын есеп
(Райнд папирусы, №26);
- Есепті пропорция құру арқылы шешу».
3
4
«Ені ұзындығының
– іне және ауданы 12-ге тең болатын тік
төртбұрыштың қабырғаларын табу керек» деген есепті алайық (Мәскеу
папирусы, №6).
- Пропорционал бөлуге берілген есептерді де қарастырған. Мысалы, Райнд
папирусындағы осындай есептердің бірі : «700 нанды 4 адамға, олардың
2 1 1
1
әрқайсысы сәйкесінше, , , және бөліктерін алатындай етіп бөліп беру
3 2 3
4
керек».
«Үштік ережесі» («трай-рашика», мағынасы: «үш орын») атты тәсіл
(Үндістанда кеңінен қолданылған).

45.

4. Натурал сандардың қасиеттері туралы алғашқы білімдер
«Фигуралы сандар»
Фигуралы сандар дегеніміз - айырмалары 1,2,3, т.с.с. сандарына
тең болатын арифметикалық прогрессия мүшелерінің тізбектелген
қосындысын құрайтын сандар.
1, 3, 6, 10, … сандары үшбұрышты сандар деп аталады, себебі
оларды тең қабырғалы үшбұрыш қабырғаларында жататын нүктелер
түрінде кескіндеуге болады.
1, 4, 9, 16, … сандары квадрат сандар, ал 1, 5, 12, 22, … сандары
бес бұрышты сандар деп аталады.
Пифагоршылар кубтық сандар (1, 8, 27, …) мен пирамидалық
сандарды (1, 4, 10, 20, …) да анықтаған.

46.

- 2-ге бөлінгіштік белгісі ежелгі Мысырда және Үндістанда белгілі болған.
Сонымен қатар үндістандықтар 5-ке бөлінгіштік белгісін де білген;
- вавилондықтар қабырғалары (3,4,5), (5,12,13,)
болатын тік бұрышты үшбұрыштарды сала білген.
(8,15,17) және т.с.с.
-«Екі санның көбейтіндісі, олардың ең болмағанда біреуі екіге бөлінгенде
және тек сонда ғана екіге бөлінеді» (пифагоршылар);
- «Евклид алгоритмі», бөлінгіштік теориясының негізгі теоремалары, жай
сандардың шексіз көп болатындығы туралы Евклид теоремасы, өзара жай
сандар, екі санның ең кіші ортақ еселігі, кемел сандар және т.б.
ұғымдардың анықтамалары келтірілген (Евклид «Негіздер»);
-жай сандарға қатты мән беріліп, оларға қатысты кейбір аса маңызды
теоремалардың дәлелдемелері келтірілген (Евклид «Негіздер»);
- «Эратосфен елегі»;
- «Ең үлкен жай сан болмайды» деген теореманы тұжырымдап, оны
дәлелдеп берді (Евклид), т.б.

47.

Сонымен,
қорыта
айтқанда,
ежелгі
замандардан бастап, IX ғ. дейін мына сияқты
математикалық білімдер жинақталды:
1. Натурал сан ұғымы туралы түсінік пен санау
жүйелері қалыптасты;
2. Есептеу мәдениетінің нышандары пайда болды;
3. Есептерді шешудің ескілікті әдістері ойлап
табылды;
4. Натурал сандардың қасиеттері туралы алғашқы
білімдер жүйеге түсіріле бастады.