Похожие презентации:
История чисел
1.
История чисел..
2.
Кто хочет ограничитьсянастоящим, без знания прошлого,
тот никогда его не поймет…
Г.В.Лейбниц
3.
Развитие представления о понятии "число".Пифагор говорил: «Все вещи можно представить в виде
чисел».
Аристотель называл число «началом и сущностью вещей, их
взаимодействием и состоянием».
У китайцев нечетные числа – это Ян (небо благоприятность),
четные
числа
–
Инь
(земля,
изменчивость
и
неблагоприятность).
Нечетность
символизирует
незавершенность, постоянное продолжение, то есть все то, что
не имеет конца, относятся к области вечного.
Числа – символ порядка. Реки, деревья и горы представляют
собой материализованные числа.
4. Появление цифр. Системы счисления.
Цифры – это знаки, с помощью которых записывают числа.Система счисления или нумерация – это способ записи чисел с
помощью цифр.
Системы счисления
Позиционные
Унарные
Непозиционные
5. Унарные системы
Число образуется путем повторения одного знака,символизирующего единицу.
=
Единичная система счисления 10 - 11 тыс. лет до н. э.
6. Непозиционные системы счисления.
Система счисления называется непозиционной, если в нейколичественные значения символов, используемых для записи
чисел, не зависят от их положения (места, позиции) в коде
числа.
В непозиционных системах для представления числа
используется сложение всех цифр, по-английски сложение – add.
Поэтому другое название этих систем - аддитивные.
Непозиционные системы счисления имеют ряд существенных
недостатков:
1. существует постоянная потребность введения новых знаков
для записи больших чисел;
2. невозможно представлять дробные и отрицательные числа;
3. сложно выполнять арифметические операции, так как не
существует алгоритмов их выполнения.
7. Обозначение чисел и счет в Древнем Египте.
100 - это мерная веревка, которой измеряли земельные участкипосле разлива Нила;
1000 - это изображение лотоса;
10 000 - "в больших числах будь внимателен!" – говорит
поднятый вверх указательный палец;
100 000 - это головастик;
1 000 000 - человек с поднятыми вверх руками;
10 000 000 - египтяне поклонялись Амону Ра, богу Солнца, самое
большое свое число они изобразили в виде восходящего солнца.
1
10
100
1000
10000
100000
1000000
10000000
8.
Записывались цифры числа начиная с больших значений изаканчивая наименьшими. Если десятков, единиц, или какого-то
другого разряда не было, то переходили к следующему разряду.
Особую роль у египтян играло число 2 и его степени. Умножение
и деление они проводили путем
последовательного удвоения и сложения чисел и в результате
расчеты выглядели довольно громоздко.
Например, для записи целого числа 23145, достаточно
записать в ряд два иероглифа, изображающие десять тысяч,
затем три иероглифа для тысячи, один – для ста, четыре – для
десяти и пять иероглифов для единицы:
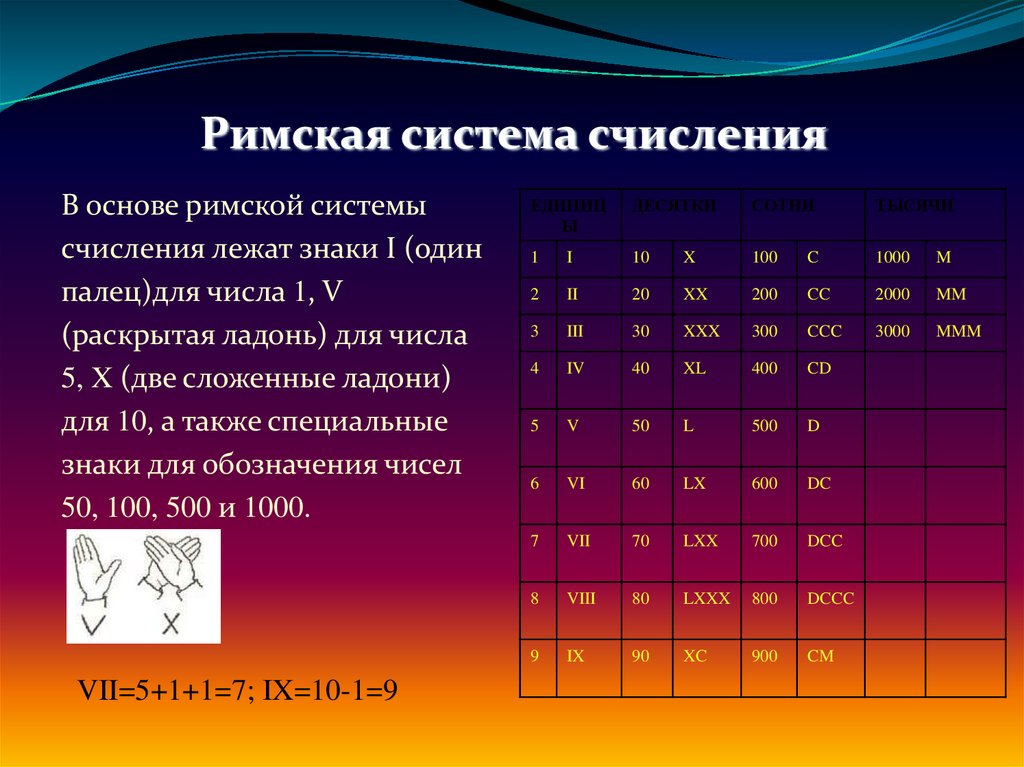
9. Римская система счисления
В основе римской системысчисления лежат знаки I (один
палец)для числа 1, V
(раскрытая ладонь) для числа
5, X (две сложенные ладони)
для 10, а также специальные
знаки для обозначения чисел
50, 100, 500 и 1000.
VII=5+1+1=7; IX=10-1=9
ЕДИНИЦ
Ы
ДЕСЯТКИ
СОТНИ
ТЫСЯЧИ
1
I
10
X
100
C
1000
M
2
II
20
XX
200
CC
2000
MM
3
III
30
XXX
300
CCC
3000
MMM
4
IV
40
XL
400
CD
5
V
50
L
500
D
6
VI
60
LX
600
DC
7
VII
70
LXX
700
DCC
8
VIII
80
LXXX
800
DCCC
9
IX
90
XC
900
CM
10. Алфавитные системы счисления. Древнегреческая нумерация.
В Древней Греции числа 1,2,….9 обозначали первыми девятьюбуквами греческого алфавита: ά (Альфа) = 1, β (Бета) = 2, γ
(Гамма) = 3 и т.д.. Для обозначения десятков применялись
следующие девять букв, для сотен последние 9 букв. Для того
чтобы отличить цифры от букв, над буквами ставили черточку.
500 30 2
2 500 30
500 2 30
11. Славянская кириллическая нумерация
Знак, обозначающий цифру («титло»)12. При Петре I возобладала так называемая арабская нумерация, которой мы пользуемся и сейчас.
Остальные числа записывались буквами слева направо.Например, числа 5044 или 1135 имели соответственно
обозначение.
Тысячи обозначались теми же буквами с «титлами», что и
первые девять цифр, но слева внизу у них ставился специальный
знак.
- 1000
- 2000
- 7000
13.
Десятки тысяч назывались «тьмами», их обозначали, обводязнаки единиц кружками : - 10 000;
- 20 000;
- 50 000.
Сотни тысяч назывались «легионами», их обозначали, обводя
знаки единиц кружочками из точек:
-100 000;
- 200 000.
Миллионы назывались «леордами», их обозначали, обводя
знаки единиц кружочками из лучей запятых:
или
Десятки миллионов назывались «воронами» их обозначали,
обводя знаки единиц кружками из крестиков:
- 10000000
Сотни миллионов назывались «колодами», буква заключалась в
квадратные скобки:
В приведенной системе обозначения чисел не шли дальше
тысяч миллионов. Такой счет назывался «малый счет».
14. Позиционные системы счисления.
Система счисления называется позиционной, если количественныезначения символов, используемых для записи чисел, зависят от их
положения (места, позиции) в коде числа.
Например, число 3333 – три тысячи триста тридцать три.
Первая тройка слева - это три тысячи, вторая - три сотни, третья три десятка, четвертая – три единицы. Число 3333 можно представить
в таком виде 3*1000 + 3*100 + 3*10 + 3. Т.е. для представления этого
числа используется умножение (по – английски multiplication),отсюда
название этой системы мультипликативная.
Основные достоинства любой позиционной системы счисления
– простота выполнения арифметических операций и ограниченное
количество символов, необходимых для записи любых чисел.
15. Вавилонская система счисления.
Простейшими цифрами в их системе служили два знака:вертикальный
клин
для
обозначения
1
и
горизонтальный клин для 10. Числа от 1 до 59
записывались с помощью этих двух знаков, как в
обычной иероглифической системе. Например: число 23
изображали так: .
Данная система называлась шестидесятеричной.
Число 60 снова обозначалось знаком , например число
92 записывали так:
. Промежуточные
разряды обозначались специальным знаком , который
выполнял роль нуля, но при этом отсутствие младших
разрядов не обозначалось никак. Так, число могло
обозначать и 3 и 180 = 3*60 и 10 800 = 3*60*60. Различать
такие числа можно было только по смыслу.
Отголоски этой системы проявляются в
обыкновении делить час на 60 мин, 1 мин на 60 секунд,
полный угол на 360 градусов.
16. Древнекитайская десятеричная система счисления.
Возникла эта система около 4 000 тысяч лет тому назад в Китае.Она является одной из старейших и самых прогрессивных, так
как в нее заложены такие же принципы, как и в современную
«арабскую», которой мы пользуемся. Числа записывались слева
направо, от больших к меньшим. Для обозначения пустого
разряда использовался специальный знак – аналог нашего нуля.
Интересен тот факт, что первыми изобрели нуль во всех его
смыслах индийские математики в VII века н.э. , до этого он
выполнял роль пробела.
Пример мультипликативной (используется умножение),
десятичной, позиционной записи.
5
* 100 + 4 * 10 + 8 = 548
17. История «арабских» чисел.
История привычных «арабских» чисел запутана и возниклаблагодаря древним астрономам, их точным расчетам. Примерно во II
веке до н.э. греческие астрономы познакомились с наблюдениями
вавилонян, переняли их позиционную систему счисления. Целые
числа они записывали не с помощью клиньев, а в своей алфавитной
нумерации. Для обозначения нуля использовали первую букву
греческого слова Ouden - ничто. Между II и VI веками н.э. индийские
астрономы познакомились с греческой астрономией, переняв
шестидесятеричную систему и круглый греческий нуль, соединили
греческую нумерацию с десятичной мультипликативной системой
взятой из Китая. Арабы, в свою очередь первыми оценили, усвоили и
и перенесли ее в Европу, упростили знаки, и они приобрели вид
, получив название арабской. В XII веке нашей эры она
распространилась по всей Европе, так как была удобнее и проще.
Слово «цифра» тоже перешло к нам от арабов по наследству нуль
или «пусто», называли «сифра». Сейчас цифрами называются все
десять знаков для записи чисел.
18.
Позиционных систем счисления достаточно много: двоичная,пятеричная, восьмеричная, десятичная, двенадцатеричная,
двадцатеричная, шестидесятеричная и т.д. и каждая из них имеет
свою историю.
Основание системы счисления – это число, на основе которого
ведется счет.
Например, если основание системы счисления равно десяти, то
минимальная счетная группа этой системы счисления равна 10, это
значит, что, сосчитав какие-либо предметы до десяти, мы считаем
снова с единицы, но при этом запоминаем число десятков. В нашей
«арабской» системе основанием является число десять.
Десятеричная и пятеричная система возникла от того факта, что на
одной руке человека пять пальцев, на обоих руках 10 пальцев. Если
добавить пальцы и на ногах, то двадцатеричная система.
Происхождение двенадцатеричной системы тоже связано со
счетом на пальцах. Считали большой палец руки и фаланги
остальных четырех пальцев. Если двенадцать умножить на пять
получим шестидесятеричную систему.
19. Двоичная система счисления.
Перевод целых чисел из двоичной системы счисления в десятичную:Каждая предыдущая цифра в 2 раза больше последующей:
1 2 4 8 16 32 64 и т.д.
Пусть имеется число 1111012, его можно представить так:
1111012 =1*1 + 0*2 + 1*4 + 1*8 + 1*16 + 1*32 = 6110
или каждый символ этого числа умножить на основание системы
счисления, возвести в степень соответствующую положению символа
в записи числа и все произведения сложить.
Перевод целых десятичных чисел в двоичный код:
Данный способ основан на записи остатков от
деления исходного числа и получаемых частных
на 2, продолжаемого до тех пор, пока очередное
частное не окажется равным 0.
7510 = 10010112
20. Двоичная система счисления.
Применяется в технических устройствах. Так, для электронногохранения данных в памяти компьютера удобны две цифры 1 и 0,
так как они требуют только двух состояний электронной схемы –
«включено» и «выключено».
1 0 1 1
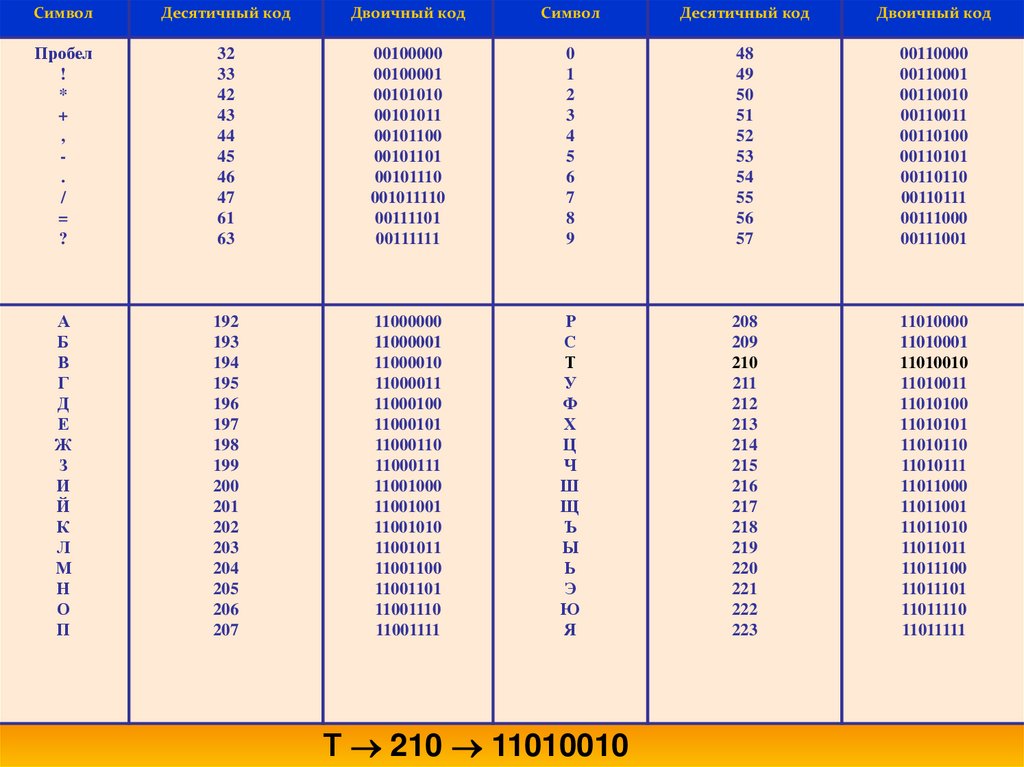
Каждый символ представляется цепочкой из 8 нулей и
единиц (всего существует 256 цепочек). Такое представление
называется двоичным или цифровым кодированием.
Соответствие символов и кодов задается с помощью
специальных кодовых таблиц.
21.
СимволДесятичный код
Двоичный код
Символ
Десятичный код
Двоичный код
Пробел
!
*
+
,
.
/
=
?
32
33
42
43
44
45
46
47
61
63
00100000
00100001
00101010
00101011
00101100
00101101
00101110
001011110
00111101
00111111
0
1
2
3
4
5
6
7
8
9
48
49
50
51
52
53
54
55
56
57
00110000
00110001
00110010
00110011
00110100
00110101
00110110
00110111
00111000
00111001
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
11000000
11000001
11000010
11000011
11000100
11000101
11000110
11000111
11001000
11001001
11001010
11001011
11001100
11001101
11001110
11001111
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Щ
Ъ
Ы
Ь
Э
Ю
Я
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
11010000
11010001
11010010
11010011
11010100
11010101
11010110
11010111
11011000
11011001
11011010
11011011
11011100
11011101
11011110
11011111
Т 210 11010010
22. Двоичное кодирование графической информации
Черно-белое изображение:0000000000011100
1000000100000110
1100001100000011
1111111100000011
1101101100000011
1111111100000011
1111111111111110
0111111011111110
0001100011000110
0000000011000110
0000000111001110
0000000111001110
0 – белая клетка
1 – черная клетка
23. Цветное изображение
Каждый пиксель имеет цвет. Все цвета можно пронумеровать, акаждый номер перевести в двоичный код.
Пиксель
24. Пятеричная система счисления.
В качестве вычислительного инструмента у человека былипальцы, поэтому и счет чаще всего вели группами по 5 или
по 10 предметов.
Индейцы племени майя в Америке считали пятерками: одна
пятерка – единица следующего разряда, пять пятерок – новый
разряд и т.д., соответственно они пользовались пальцами одной
руки.
Рассмотрим пятеричную систему счисления:
0 1 2 3 4 10 11 12 13 14 20 21 22 23 24 30 31 32 33 34 40 41 42 43 44
Переведем число 34 из пятеричной систему счисления в
десятичную: 345 = 3*51 + 4*50 = 15+4=1910
и наоборот из десятичной в пятеричную:
1910 = 345
25. Десятичная система счисления.
Система записи чисел, которой мы привыкли пользоваться вповседневной жизни. В ней используется десять различных знаков
(цифры 0,1,2,3….9).
Из двух написанных рядом одинаковых цифр предыдуща цифра в
10 раз больше последующей.
В десятичном числе 255 = 2*100+5*10+5*1 цифры «5», находящаяся
на разных позициях, имеют различные количественные значения –
5 десятков и 5 единиц. При перемещении цифры на соседнюю
позицию, ее «вес» изменится в 10 раз.
Перевод чисел из одной системы в другую
осуществляется по аналогии с предыдущими системами.
Позиционный принцип и цифровое обозначение могут быть
приспособлены к системе счисления с любым основанием,
кроме единицы.
26. Восьмеричная система счисления.
Используются цифры от 0 до 7....
Шведский король Карл XII в 1717 г. увлекся
этой системой и собирался ввести ее как
общегосударственную
27. Двенадцатеричная система счисления.
Число 12 (дюжина)была широко распространена и в Европе, ив России, но постепенно уступила свое место десятке. Для счета
использовались только четыре пальца одной руки, однако при
этом учитывали, что каждый палец состоит из трех фаланг.
Дюжина прочно вошла в нашу жизнь:
В сутках две дюжины часов
Час делится на пять дюжин минут
Столовые сервизы на 6
или 12 персон
Набор карандашей или
фломастеров: 6, 12 или 24
28.
Изучая исторические процессы развития общества мывыяснили, что понятие числа прошло длинный исторический
путь развития и наука о числах и действиях над ними
необходима для прогрессивного развития человеческого
общества.
Нами была установлена зависимость между возникновением
чисел и необходимостью их выражения знаками.
Мы узнали о существовании различных теорий о происхождении
чисел и пришли к выводу, что самым ценным вкладом в
сокровищницу математических знаний человечества является
употребляемый нами способ записи при помощи десяти знаков
чисел: 1,2,3,4,5,6,7,8,9,0.
В процессе исследования и с целью выявления осведомленности
одноклассников о многообразии чисел нами было проведено
анкетирование.


























 Информатика
Информатика История
История








