Тайны модуля числа

1.

2. Цель: Глубоко изучить тему «Модуль числа». Исследовать зависимость а) суммы, разности, произведения, частного от замены

компонента его
модулем;
б) расположения точек координатной
плоскости от замены координат точек
их модулем.
Задачи:
Найти и изучить материал из
истории модуля;
Рассмотреть различные
определения модуля; области
применения модуля.
Исследовать зависимость суммы, разности,
произведения, частного от замены компонента его модулем;
Исследовать зависимость расположения точек координатной
плоскости от замены координат точек их модулем..
Разработать задачник по теме
«Модуль»

3. Что же такое модуль?

Modulus(лат.) - мера
Модуль - это омоним, который имеет
множество значений и применяется в
архитектуре, физике, технике,
программировании.

4.

В архитектуре – это исходная единица
измерения, устанавливаемая для данного
архитектурного сооружения и служащая
для выражения кратных соотношений его
составных элементов.

5. В технике – это термин, применяемый в различных областях техники, не имеющий универсального значения и служащий для обозначения

различных коэффициентов и
величин, например, модуль зацепления, модуль упругости
и т.п.
Модуль объемного сжатия (в
физике) – отношение
нормального напряжения в
материале к относительному
удлинению.

6. А что же такое модуль с точки зрения математики?

Существует несколько
определений модуля.
Например:
Модуль
неотрицательного
числа равен самому
числу. Пример:|17|= 17, |25|=
25
Модуль
отрицательного
числа равен числу,

7.

Второе , известное мне определение модуля - это
расстояние от начала отсчета до точки с данной
координатой.
x 3
X=
–3
3
0
3

8. Это определение в старших классах будет выглядеть так:

|x|=
х, еслих 0
х, еслих 0
У модуля есть
обозначение. Значит, его
кто- то
придумал, но кто?
Считают, что термин
предложил Роджер Котс

9. Модуль - одна из самых интересных и многогранных тем в математике. В школьной программе очень часто встречаются задания,

содержащие модуль ,например,
в заданиях повышенной сложности,
практически все вступительные экзамены в вузы
содержат задания с модулем - это уравнения, неравенства,
графики.
Как же научиться решать такие сложные
упражнения?
Только глубоко изучив модуль!
Я решила начать с небольших исследований.

10. 1. Замена слагаемого его модулем: а + в и а + |в|

Исследование №1:
1. Замена слагаемого его модулем:
а+в
и
а + |в|
а) а = 8, в = 6
8 + 6 и 8+|6|
14 и 14
Сумма
не меняется.
б) а = -8, в = -6
-8 + (-6) и -8 + |-6|
-14
и
-2
|-8|+ (-6)
2
Сумма увеличивается.

11. 1. Замена слагаемого его модулем: а + в и а + |в|

1. Замена слагаемого его модулем:
а+в
и
а + |в|
В) а= 8,
в= - 6
8 +(- 6 ) и 8+|-6|
2
и 14
Сумма увеличилась.
б) а = -8, в = 6
-8 + 6
и -8 + |-6|
-14
и
-2
|-8|+(-6)
2
Сумма увеличивается.
Вывод:
При замене слагаемого его модулем сумма
увеличивается или остаётся без изменения.

12. Рассмотрим модуль суммы и сумму модулей:

|а + в|
и
а= 8,
|8 + (-6)|=|2|= 2
в= - 6
|8| +|-6|=14
а= -8,
|-8 + (-6)|=|-14|= 14
|а| +|в|
в= - 6
|-8| +|-6|=14
Вывод:
|а + в| ≤ |а| +|в|
Аналогичные исследования я провела для
разности, произведения и
частного и увидела как влияет модуль на
результат.

13.

Где же ещё можно использовать модуль?
Оказывается при изучении вопроса о расположении точек
в координатной плоскости.
Я решила выяснить, влияет ли модуль на расположение
точек, если координаты точек заменить их модулем.
Мне известно, что, если взять произвольную точку
М(х;у) и построить её в прямоугольной системе координат,
то она может лежать в I, II, III, IV четвертях. Это зависит
от значения х и у .
Так, точки А (3;4) В (-3;4) С (-3;-4) D (3;-4) лежат в I,
II, III, IV четвертях соответственно.
А что произойдёт, если абсциссу заменить модулем?
А ординату?
А если обе координаты заменить модулем?

14. Исследование №2 Исследование зависимости расположения точек при замене координаты точки её модулем.

Гипотеза:
расположение точки в прямоугольной системе
координат зависит от замены координаты точки
её модулем.
Эту гипотезу нужно подтвердить или
опровергнуть.
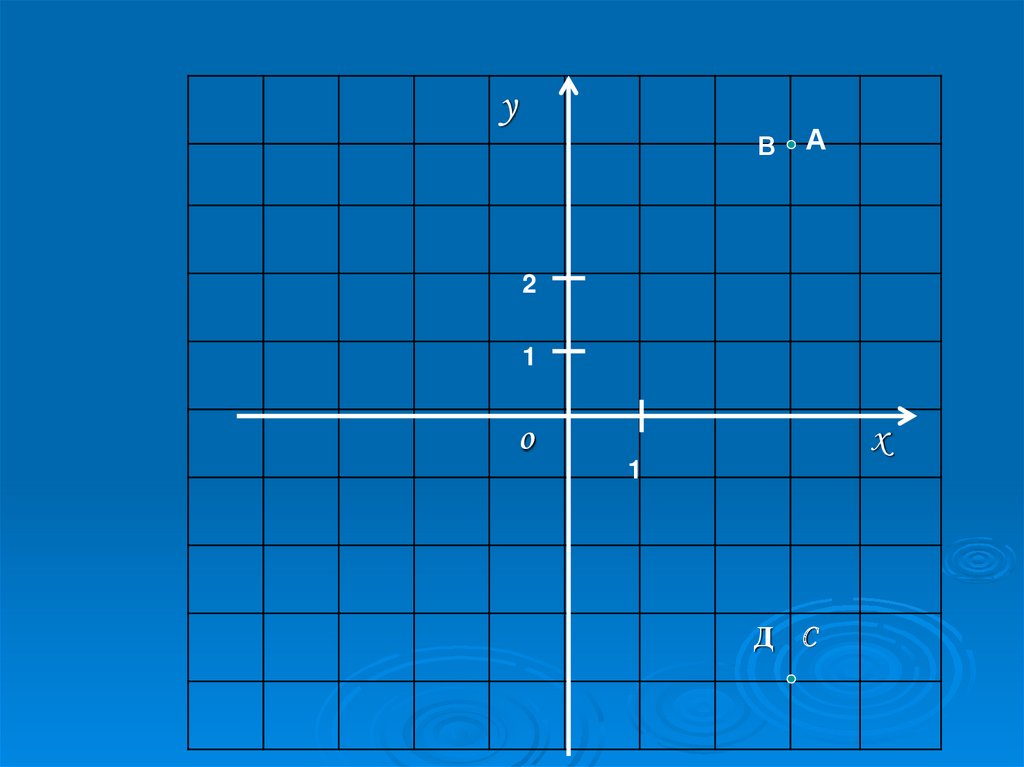
Для этого построим в системе координат точки вида
N (|x|;y) : А (|3|;4), В (|-3|;4)
С (|-3|;-4), D (|3|;-4).

15.

у
В
А
2
1
о
х
1
Д С

16.

Построив
точки, у меня возникло
предположение, что точки вида N (|x|;y)
располагаются в правой полуплоскости
системы координат. Чтобы подтвердить
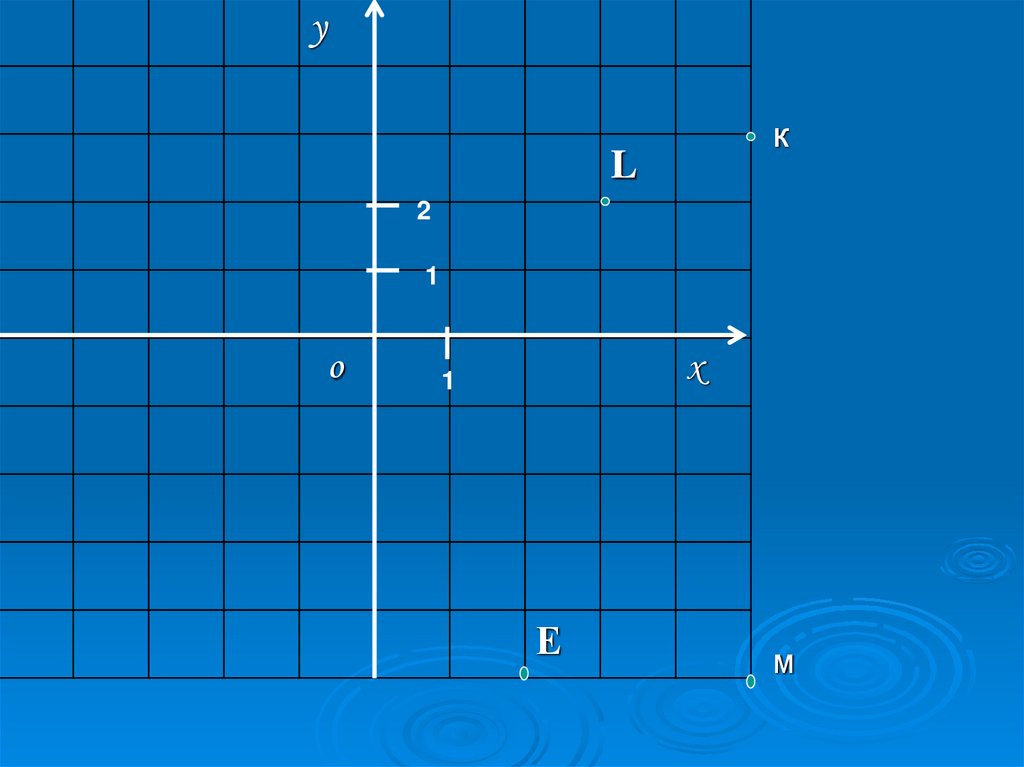
это, возьмём дополнительные точки M,
K, L, E и построим их.
М (|5|;-5) К (|-5|;3) L (|-3|;2) Е (|2|;-5)

17.

у
К
L
2
1
о
х
1
Е
М

18. Вывод:

Гипотеза подтвердилась: положение точек в
прямоугольной системе координат изменилось.
Если абсциссу точки заменить модулем, то
точки будут располагаться в правой
полуплоскости системы координат.
Если ординату точки заменить модулем, то
точки будут располагаться в верхней
полуплоскости.
Если же заменить модулем обе координаты, то
точки будут располагаться в первой четверти.

19. Использованные ресурсы:

И.И. Зубарева, А.Г. Мордкович. Математика 6.
И.И. Зубарева, М.С. Мильштейн, М.Н. Шанцева.
Математика 6.Самостоятельные работы.
Энциклопедия для детей. Аванта. Математика.
Том 11.
http://collection.edu.yar.ru/catalog/rubr/
http://festival.1september.ru/articles/
Слайд из презентации учителя математики МОУ
гимназия №1 г. Полярные зори Савченко Е. М. на
сайте:
http://www.it-n.ru/profil.aspx?cat_no=692&d_no=9658