Правовая статистика. Понятие, предмет, методы и назначение правовой статистики

1.

Тема 1.
Понятие, предмет, методы и
назначение правовой
статистики

2.

Учебные вопросы
1. Понятие и система статистики.
2. Понятие, предмет и методы правовой
статистики.
3. Закон больших чисел как математическая
основа статистических закономерностей.
4. Элементарные понятия статистики.

3.

Вопрос 1.
Понятие и система статистики

4.

В научный оборот термин «статистика» ввел
немецкий профессор Готфрид Ахенваль в 1746 г.
Так он назвал новую научную дисциплину, которую
читал в Мордургском университете.
Он рассматривал ее как отрасль государствоведения и
полагал, что ее содержание должно состоять в
описании политического состояния государств.
Поэтому он использовал в ее названии понятия,
связанные с государством:
• status — состояние, положение;
• stato — государство и
• statista — знаток государства.

5.

В середине XVIII в. словом «статистика» стали
называть фактические сведения о
государствах.
К таким сведениям относились данные о
численности и движении населения
государств, их экономике,
территориальном делении и т.д.
Со временем кроме совокупности
количественных данных, под статистикой
стали понимать процесс ее ведения, науку
о массовых явлениях, предмет
преподавания.

6.

Однако фактически статистические методы
анализа массовых явлений впервые
применили уже в XYII в. английские
«политические арифметики» Джон Граунт
(1620—1674) и Уильям Петти (1623—1687).
Дж. Граунт — родоначальник науки
демографии. Использовал статметоды, в т.ч.
перепись при изучении движения населения в
Лондоне.
У. Петти— один из основоположников
классической политической экономии.
Использовал статметоды при исчислении
народного богатства, дохода, численности и
состава населения.

7.

Термин «статистика» имеет троякое значение.
1. Статистика как совокупность сведений о
массовых явлениях в обществе и природе.
Конкретные количественные величины,
абсолютные и относительные,
раскрывают уровень, динамику или
структуру того или иного массового
явления.

8.

2. Статистика как вид практической
деятельности по сбору, обработке, анализу
и обнародованию количественной
информации.
Статистика - учет экономических,
демографических, социальных,
юридических и других массовых явлений, а
также формируемая на его основе
периодическая отчетность.

9.

3. Статистика как отрасль знаний, в которой
излагаются теоретические вопросы сбора,
сводки, группировки, измерения и анализа
количественных сведений о массовых
явлениях.
Статистика - самостоятельная наука и
основанная на ней учебная дисциплина.

10.

Статистика как наука изучает
количественную сторону
массовых явлений в целях
раскрытия их качественного
своеобразия и
закономерностей их развития в
конкретных условиях места и
времени.

11.

Статистика является наукой
универсальной.
С ее помощью можно изучать любые
массовые совокупности.
Статистика является наукой
общественной.
Статистическая наука — один из самых
мощных методов социального
познания.

12.

Система статистики
1. Общая теория статистики, которая разрабатывает
категории и методы измерения количественных
закономерностей общественной жизни.
2. Экономическая статистика, изучающая количественные
закономерности процессов воспроизводства .
3. Социальная статистика, изучающая количественную
сторону развития социальной инфраструктуры общества
(статистика здравоохранения, образования, культуры,
моральная, правовая, судебная и др.).
4. Отраслевые статистики (промышленности,
агропромышленного комплекса, транспорта, связи и
т.д.).

13.

Вопрос 2.
Понятие, предмет и методы
правовой статистики

14.

Правовая статистика является одной из
отраслей статистической
науки, которая изучает
количественную сторону
социальных явлений, связанных с
применением норм права и
реализацией
правовой ответственности.

15.

Основу правовой статистики
составляют:
• Общая теория статистики
• Правоведение — совокупность
юридических наук, которые
исследуют качественные
особенности и природу правовых
явлений.

16.

Правовая статистика характеризуется рядом
признаков:
• наука о количественной стороне явлений,
• наука о явлениях массовых,
• наука о явлениях правовых (имеющих
юридическое значение),
• раскрывает их качественное своеобразие и
тенденции,
• наука о закономерностях их развития,
• учитывает конкретные условия места и
времени.

17.

Юриспруденция отличается от других
социальных наук.
Кроме фактической реальности она имеет
еще одну реальность — писаную (законы,
другие нормативные акты, судебные
решения, живущие своей относительно
самостоятельной жизнью).
Знание правовых норм и чисто логическое
мышление не может принести знания
эмпирического мира и заменить его.

18.

Эмпирический мир права познается
в опыте на основе реальных
фактов.
Изучение фактической реальности
требует овладения
статистическими методами.

19.

Без статистических методов невозможно
изучать фактическую преступность,
судимость, административные
правонарушения, гражданско-правовые споры
и другие социально-правовые явления и
процессы.
Статистический анализ этих массовых явлений и
процессов позволяет выявить законы их
распределения и динамики, получить другую
важную информацию, необходимую для
совершенствования правовых отношений.

20.

21.

Уголовно-правовая статистика —
изучает количественную сторону
преступности, судимости и
деятельности государственных
органов по борьбе с
преступностью, предупреждению
преступных проявлений и
исправлению правонарушителей.

22.

Из истории…
Впервые распоряжение о
представлении судами
статистических сведений было
сделано во Франции в 1801 г.,
первый свод статистических
сведений составлен в 1813 г.

23.

Из истории…
В России правила о составлении
уголовных статистических записей
установлены в 1871 г.
Статистическое отделение
министерства юстиции печатало
ежегодно справки о судимости,
сборники сведений о составе судебных
установлений, «Свод сведений по делам
уголовным».

24.

Гражданско-правовая статистика —
осуществляет учёт гражданскоправовых споров, которые
находятся на разрешении судов
общей юрисдикции и
арбитражных судов, а также учет
результатов деятельности
данных органов

25.

Административно-правовая статистика —
занимается учетом административных
правонарушений по их видам,
причиненному ущербу,
характеру административных взысканий,
органам административной юрисдикции и
арбитражных судов, а также учет
результатов деятельности данных органов

26.

Методы
правовой статистики
• массовое статистическое наблюдение;
• сводка и группировка данных, полученных
при наблюдении, по качественноопределенным признакам;
• статистический количественный анализ
показателей;
• качественный анализ статистических
материалов.

27.

Вопрос 3.
Закон больших чисел как
математическая основа
статистических закономерностей

28.

Закон больших чисел - свойство
статистических закономерностей
формироваться и отчетливо
отражаться лишь в массовом процессе
и при достаточно большом числе
единиц совокупности

29.

Закон больших чисел
Закон больших чисел состоит в том, что
«вероятность отклонений среднего по
выборке от математического ожидания мала»
и что «эта вероятность стремится к нулю при
увеличении выборки».
То есть: мы можем быть в достаточной степени
уверены, что среднее по нашей выборке
достаточно близко к «истинному» среднему
(среднему по генеральной совокупности) и
таким образом хорошо его описывает.

30.

Закон больших чисел позволяет перейти от
случайного и единичного к устойчивому и
массовому и выражает связь между
случайностью и необходимостью.
Совокупность случайных причин порождает
следствие, почти не зависящее от случая, в
чем и обнаруживается закономерность,
которая не может быть выявлена при
малом числе наблюдений.

31.

Математической основой закона
больших чисел служит теория
вероятностей.
Теория вероятностей - раздел
математики, изучающий
случайные события, случайные
величины, их свойства и операции
над ними.

32.

Связь между состоянием субъекта и
конкретным видом преступного
поведения проявляется в их
удельных весах или частости
(частоте проявления).
Исходя из этой частости, можно
прогнозировать преступления.

33.

Например
Годовые отчеты о ДТП в городе свидетельствуют
о том, что 25—30% их совершается на
перекрестках.
Тем не менее, используя эту информацию,
невозможно предсказать, будут ли совершены
ДТП на каком-то конкретном перекрестке.
Однако с достаточной долей точности можно
предсказать, что в текущем году на
перекрестках будет совершено определенное
количество ДТП.

34.

Следует различать
теоретическую и
эмпирическую вероятность

35.

Теоретическая вероятность
Вероятность события – это количественная мера,
которая вводится для сравнения событий по
степени возможности их появления.
Событие – это любой исход или совокупность исходов
какого – либо вероятностного эксперимента.
Вероятностью события А – Р(А) – называется
отношение числа m исходов, при которых случается
событие А, к числу n всех возможных исходов в
условиях данного вероятностного эксперимента.

36.

Пример
Теоретическая вероятность того, что
после одного броска монеты выпадет
орел, может быть рассчитана как:
P( выпадает Орел ) = (только в одном
случае при броске может выпасть
Орел) / (Два возможных исхода (орел
и решка) = 1/2

37.

Теоретическая (математическая)
вероятность - отношение
количества шансов,
способствующих появлению
изучаемого события, к количеству
всех шансов, как
благоприятствующих, так и не
благоприятствующих его
наступлению

38.

Шанс
Термин "шанс" пришел из теории
азартных игр, где при помощи
данного понятия обозначали
отношение выигрышных
позиций к проигрышным

39.

Шанс
• Отношение вероятности того, что событие
произойдёт, к вероятности того, что
событие не произойдёт.
• Например, если вероятность события равна
0.2 (20%), то вероятность того, что оно не
произойдет равно 0.8 (80%).
• Тогда шанс равен:

40.

Вероятность=0,5
Шанс=1:1=1

41.

Эмпирическая вероятность
(частость) - отношение числа
фактически наступивших
явлений к общему числу
возможных

42.

Например, при фактическом десятикратном
бросании монеты 3 раза выпал герб и 7 раз
— решка.
Эмпирическая вероятность выпадения герба 3 : 10=0,3,
выпадения решки –
7 : 10 = 0,7.
Фактические результаты существенно
расходятся с теоретическими.

43.

Такое расхождение обусловлено малым
числом наблюдений, где действие
постоянных причин, определяющих
равную возможность выпадения обеих
сторон монеты (симметричность,
расположение центра тяжести в середине и
т.п.), искажено случайными причинами
(порывами ветра, разной силой бросания и
т.п.).

44.

Французский естествоиспытатель XVIII в.
Бюффон подбрасывал монету 4040
раз.
Герб выпал 2048 раз, решка — 1992
раза.
Опытная вероятность (частость)
выпадения герба была равна 0,5069
при теоретической вероятности 0,5000
(отклонения незначительны).

45.

При малом числе наблюдений
фактические результаты (опытная
вероятность) могут существенно
отклоняться от математической
вероятности, в то время как при
большом числе наблюдений они
становятся близки к теоретическим

46.

Закон больших чисел лежит а основе
выборочного метода, позволяющего при
неполном исследовании единиц
совокупности и заведомо заданной ошибке
представительности (репрезентативности)
выявить и измерить основные тенденции и
закономерности, свойственные всей
генеральной совокупности.
На теории вероятностей базируются
статистические методы анализа,
криминологического прогнозирования
преступности и решения других задач.

47.

Вопрос 4.
Элементарные понятия статистики

48.

Что такое переменные?
Переменные - это то, что можно
измерить, контролировать или
чем можно манипулировать в
исследованиях

49.

Большинство эмпирических
исследований данных можно
отнести к одному из двух типов:
• исследование зависимостей;
• экспериментальные
исследования.

50.

Исследование зависимостей
В исследовании корреляций вы не влияете
на какие-либо переменные, а только
измеряете их и хотите найти зависимости
(корреляции) между некоторыми из
измеренных переменных.
Например, между уровнем дохода и
коэффициентом преступной активности.

51.

Экспериментальные исследования
В экспериментальных исследованиях вы варьируете
некоторые переменные и измеряете воздействия
этих изменений на другие переменные.
Например, в медицине исследователь может
искусственно увеличить кровяное давление, а затем
измерить уровень холестерина.
В правовых исследованиях использование
эксперимента ограничено.
Анализ данных в экспериментальном исследовании
также приходит к вычислению "корреляций" между
переменными, на которые воздействуют, и теми
переменными, на которые влияет это воздействие.

52.

Экспериментальные исследования
Экспериментальные данные снабжают
нас более качественной информацией.
Только экспериментальные данные
могут убедительно
продемонстрировать наличие
причинных связей между
переменными.

53.

Экспериментальные исследования
Например, если вы обнаружили, что всякий
раз, когда изменяется переменная А,
изменяется и переменная В, то можете
сделать вывод - “переменная А оказывает
влияние на В.”
Результаты корреляционного исследования
могут быть проинтерпретированы в
каузальных (причинных) терминах на
основе некоторой теории, но сами по себе
не могут отчетливо доказать причинность.

54.

Зависимые и независимые
переменные
Независимыми переменными
называются переменные, которые
варьируются исследователем.
Зависимая переменная —измеряемая
переменная, изменения которой
связывают с изменениями
независимой переменной.

55.

Термины зависимая и независимая переменная
применяются в основном в экспериментальном
исследовании, где экспериментатор
манипулирует некоторыми переменными.
В этом смысле они “независимы” от реакций,
свойств, намерений и т.д. присущих объектам
исследования.
Некоторые другие переменные, как предполагается,
должны "зависеть" от действий экспериментатора
или от экспериментальных условий.
Зависимость проявляется в ответной реакции
исследуемого объекта.

56.

Термин «зависимые и независимые»
переменные используются также в
исследованиях, где вы не варьируете
независимые переменные, а только
приписываете объекты к “экспериментальным
группам”, основываясь на некоторых их
предэкспериментальных свойствах.
Например, если в обвиняемые разного
социально-экономического положения (СЭП)
сравниваются по вероятности вынесения
оправдательного приговора, то СЭП можно
назвать независимой переменной, а
вероятность оправдания - зависимой.

57.

Переменные различаются также тем
"насколько хорошо" они могут быть
измерены, как много измеряемой
информации обеспечивает шкала их
измерений.
Это определяется:
• уровнем ошибок;
• типом шкалы, в которой проведено
измерение.

58.

Типы шкал
• Номинальная;
• Порядковая (ординальная);
• Интервальная;
• Относительная (шкала
отношения).

59.

Номинальная шкала
Номинальные (категориальные) переменные
используются только для качественной
классификации.
Это означает, что данные переменные могут
быть измерены только в терминах
принадлежности к некоторым существенно
различным классам, при этом вы не
сможете определить количество или
упорядочить эти классы.

60.

Пример
Вы можете сказать только, что 2 индивидуума
различимы в терминах данной переменной
А (например, принадлежат к разным
расам), но не сможете сказать, у кого из них
данное качество выражено в большой
степени.
Типичными примерами номинальных
переменных являются пол,
национальность, цвет глаз, город и т.д.

61.

Порядковая (ординальная) шкала
Порядковые (ординальные) переменные позволяют
ранжировать (упорядочить) объекты, указав какие
из них в большей или меньшей степени обладают
качеством, выраженным данной переменной.
Однако они не позволяют сказать “на сколько больше”
или “на сколько меньше”.
Типичный пример - социоэкономический статус
семьи м.б. определен на уровне:
верхнем, среднем, выше среднего.
Однако сказать, что разница между ними равна,
скажем, 18% мы не сможем.

62.

Интервальная шкала
Интервальные переменные позволяют не
только упорядочивать объекты измерения, но
и численно выражать и сравнивать различия
между ними.
Например, температура, измеренная в градусах
Цельсия, образует интервальную шкалу.
Вы можете не только сказать, что температура 40
градусов выше, чем температура 30 градусов,
но и что увеличение температуры с 20 до 40
градусов вдвое больше увеличения
температуры от 30 до 40 градусов.

63.

Относительная шкала
Относительные переменные похожи на
интервальные переменные.
В дополнение ко всем свойствам интервальных
переменных, их характерной чертой является
наличие определенной точки абсолютного
нуля.
Для этих переменных являются обоснованными
предложения типа: х в два раза больше, чем у.
Типичными примерами шкал отношений
являются измерения времени или
пространства.

64.

В большинстве статистических
процедур не делается различия
между свойствами
интервальных и относительных
шкал

65.

Зависимости между переменными
Две или более переменных связаны (зависимы)
между собой, если наблюдаемые значения
этих переменных распределены
согласованным образом.
Переменные зависимы, если их значения
систематическим образом согласованы друг с
другом в имеющихся у нас наблюдениях.
Например, переменные Рост и Вес являются
зависимыми, потому что обычно высокие
индивиды тяжелее низких.
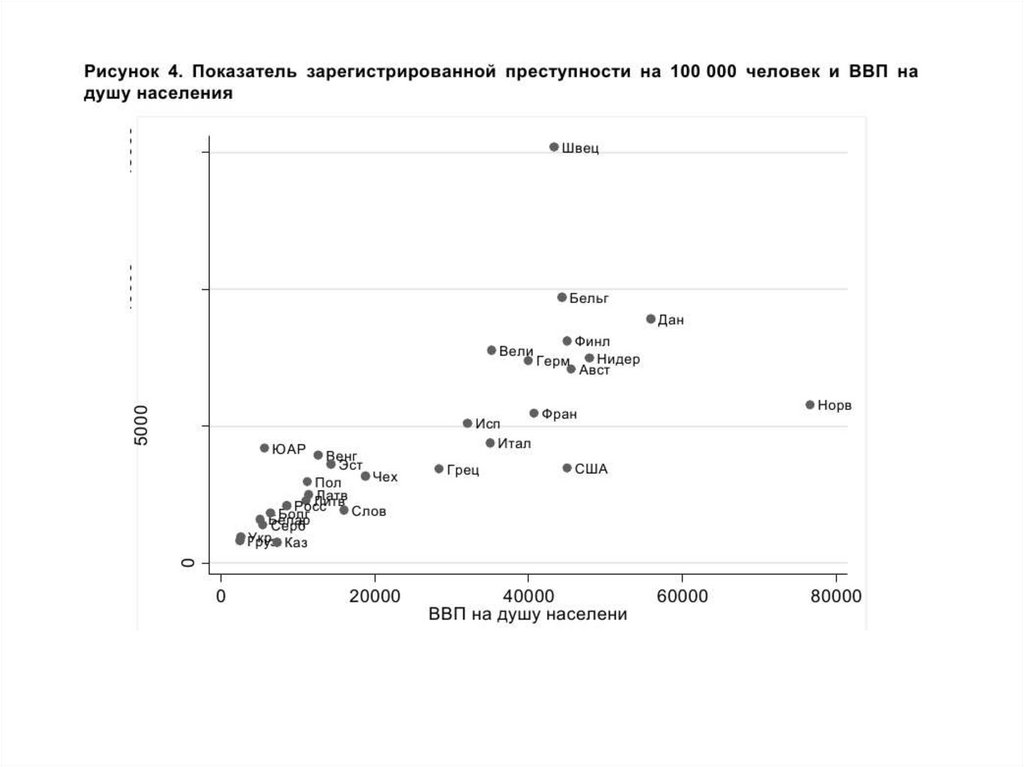
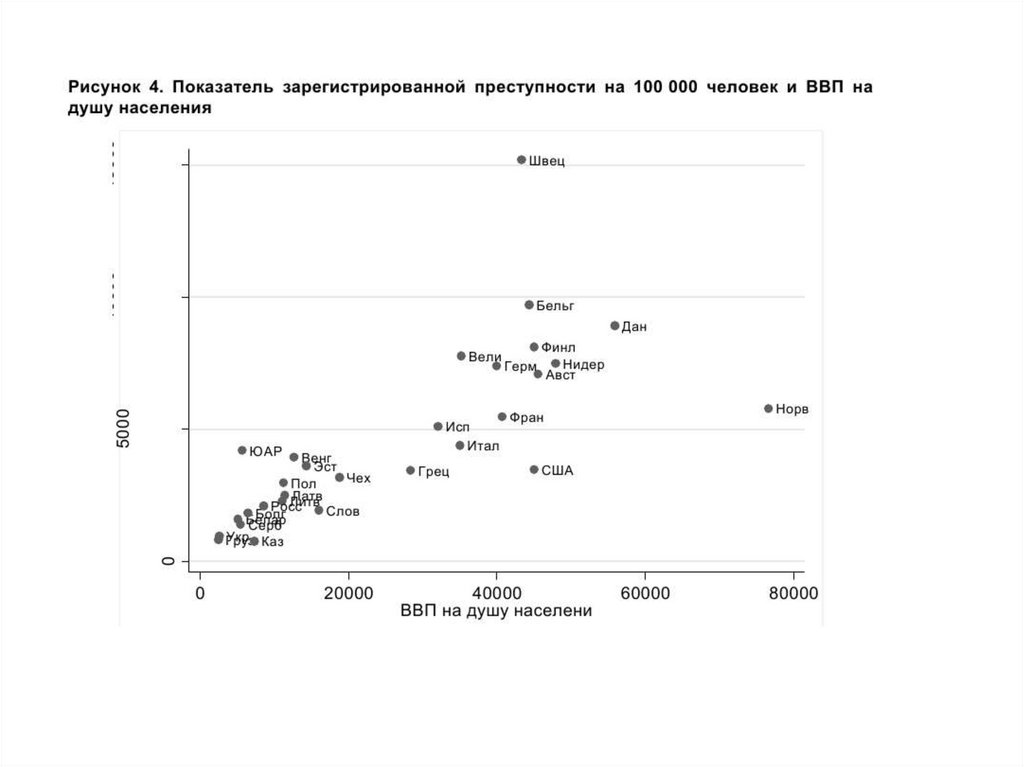
ВВП на душу населения по странам связаны с
уровнем зарегистрированной преступности.

66.

67.

Важность зависимостей
Конечная цель всякого исследования или
научного анализа – нахождение связей
(зависимостей) между переменными.
Философия науки учит, что не существует иного
способа представления знания, кроме как в
терминах зависимостей между количествами
или качествами.
Развитие науки всегда заключается в
нахождении новых зависимостей между
переменными.

68.

Само назначение статистики состоит в
том, чтобы помочь оценить
зависимости между переменными.

69.

70.

Величина зависимости
Величину зависимости легче понять и измерить,
чем надежность.
Например, если каждый мужчина в
выборке имел значение WCC выше чем любая
женщина, то можно сказать, что величина
зависимости между двумя переменными (Пол
и WCC) очень высокая.
Таким образом, возможно предсказать значения
одной переменной по значениям другой.

71.

72.

73.

Надежность (“истинность ” )
Надежность взаимозависимости
непосредственно связана с
репрезентативностью той определенной
выборки, на основе которой строятся выводы.
Надежность говорит, насколько вероятно, что
зависимость, подобная найденной вами, будет
вновь обнаружена (иными словами,
подтвердится) на данных другой выборки,
извлеченной из той же самой генеральной
совокупности.

74.

Конечной целью почти никогда
не является изучение данной
конкретной выборки.
Выборка представляет интерес
лишь постольку, поскольку она
дает информацию обо всей
популяции.

75.

При определенных условиях надежность
найденных зависимостей между
переменными выборки можно
количественно оценить и представить
с помощью стандартной
статистической меры, которая
называется
р-уровнем или статистическим уровнем
значимости.

76.

Статистическая значимость
(р-уровень)
Статистическая значимость результата представляет
собой оцененную меру уверенности в его
“истинности” (в смысле “репрезентативности
выборки”).
р-уровень это показатель, находящийся в убывающей
зависимости от надежности результата.
Более высокий р-уровень соответствует более
низкому уровню доверия к найденной в выборке
зависимости между переменными.
р-уровень - вероятность ошибки, связанной с
распространением наблюдаемого результата на всю
генеральную совокупность.

77.

Пример
р-уровень = 0.05 показывает, что
имеется 5% вероятность того, что
найденная в выборке зависимость
между переменными является лишь
случайной особенностью данной
выборки.

78.

Пример
То есть, если данная зависимость в популяции
отсутствует, а вы многократно проводили
бы подобные эксперименты, то примерно в
одном из двадцати повторений
эксперимента можно было бы ожидать
такой же или более сильной зависимости
между изучаемыми переменными.
Во многих исследованиях р-уровень = 0.05
рассматривается как “приемлемая граница”
уровня ошибки.

79.

Как определить, является ли
результат действительно значимым?

80.

Выбор определенного уровня значимости, выше
которого результаты отвергаются как ложные,
является достаточно произвольным.
На практике решение обычно зависит от того,
был ли результат предсказан до проведения
опыта или обнаружен апостериорно в
результате многих анализов и сравнений,
выполненных с множеством данных, а также
на традиции имеющейся в данной области
исследований.

81.

Обычно во многих областях результат р < 0.05
является приемлемой границей
статистической значимости.
Однако этот уровень все еще включает
довольно большую вероятность ошибки
(5%).
Результаты, значимые на уровне р < 0.01
обычно рассматриваются как статистически
значимые.
Результаты с уровнем р < .005 или р < .001
как высоко значимые.

82.

Статистическая значимость
и число испытаний
Чем большее число анализов вы
провели над совокупностью
данных, тем большее число
результатов среди них имеют шанс
удовлетворить выбранному
уровню значимости.

83.

Например
Если вычисляют корреляции между 10
переменными (т.е. имеется 45 различных
коэффициентов корреляции), то можно
ожидать, что примерно два коэффициента
корреляции (один на каждые 20) случайно
окажутся значимыми на уровне р < 0.05,
даже если переменные совершенно
случайны и некоррелированы в
генеральной совокупности.

84.

Вывод
Исследователь должен с
осторожностью оценивать
надежность неожиданных
находок!

85.

Величина зависимости между
переменными в сравнении с надежностью
зависимости
Чем больше величина зависимости между
переменными в выборке обычного объема, тем
более она надежна.
Если предполагать отсутствие зависимости между
соответствующими переменными в популяции, то
наиболее вероятно ожидать, что в исследуемой
выборке связь между этими переменными также
будет отсутствовать.

86.

Величина зависимости между
переменными в сравнении с надежностью
зависимости
Чем более сильная зависимость
обнаружена в выборке, тем менее
вероятно, что этой зависимости
нет в популяции, из которой она
извлечена.

87.

Объем выборки влияет на
значимость зависимости
Если наблюдений мало, то имеется мало
возможных комбинаций значений этих
переменных и таким образом,
вероятность случайно обнаружить
комбинацию значений,
показывающую сильную зависимость,
относительно высока.

88.

Пример
Если вы исследуете зависимость двух
переменных (Пол: мужчина/женщина и кол-во
лейкоцитов: высокий/низкий) и имеете только
4 субъекта в выборке (2 мужчины и 2
женщины), то вероятность того, что чисто
случайно вероятность того, что оба мужчины
имеют высокий WCC, а обе женщины - низкий
WCC, или наоборот, - равна 1/8.
Вероятность подобного совпадения для 100
субъектов равна практически нулю.

89.

Пример
Имеются 2 населенных пункта (нп). В первой из
них каждый день совершается 120
правонарушений, во втором только 12.
В среднем отношение числа мужчин и женщин,
совершающих правонарушения, рождающихся
в каждом населенном пункте 1/1.
Однажды в одном из нп правонарушений с
участием женщин было зарегистрировано
вдвое больше, чем с участием мужчин.
В каком из нп это событие более вероятно?

90.

Такое событие гораздо более
вероятно для маленького
населенного пункта.
Вероятность случайного отклонения
(от среднего популяции)
возрастает с уменьшением объема
выборки.

91.

Слабые зависимости могут быть значимо
доказаны только на больших выборках.
Даже если выборка совершенно
репрезентативна, эффект не будет
статистически значимым, если выборка
мала.
Если зависимость "объективно» очень
сильная, тогда она может быть обнаружена
с высокой значимостью даже на очень
маленькой выборке.

92.

Пример
Пусть монета слегка несимметрична, и при
подбрасывании орел выпадает чаще решки
(например, 60% против 40%).
10 подбрасываний монеты было бы не
достаточно, чтобы убедить кого бы то ни
было, что монета асимметрична, даже если
был бы получен результат 6 орлов и 4
решки.

93.

Пример
Но представьте, что монета настолько
несимметрична, что всякий раз, когда вы ее
бросаете, выпадает орел.
Если вы бросаете такую монету 10 раз, и всякий
раз выпадает орел, большинство людей сочтут
это убедительным доказательством того, что в
популяции, состоящей из бесконечного числа
подбрасываний этой монеты орел будет
встречаться чаще, чем решка.
Таким образом, если зависимость сильная, она
может быть обнаружена с высоким уровнем
значимости даже на малой выборке.