Похожие презентации:
Статистика: понятие, методы, предмет, организация. Лекция №1
1.
Колмакова Екатерина Микаеловна,к.э.н.
2.
Содержание:Лекция №1: Статистика: понятие,
методы, предмет, организация.
Лекция №2: Статистическое
наблюдение.
Лекция №3: Статистическая сводка
и группировка статистических
данных. Статистические таблицы.
3.
Содержание:Лекция №4: Графическое
изображение статистических
данных.
Лекция №5: Статистические
показатели и величины.
4.
Лекция №11. Понятие статистики.
2. Предмет статистики.
3. Объект статистики
4. Исходные понятия
5. Методы статистики
6. Статистическое исследование
7. Статистические организации
5.
СТАТИСТИКА имеет три значения:1
Отрасль практической деятельности, направленная
на получение, обработку и анализ массовых данных
о различных явлениях и процессах общественной
жизни
2
Цифровой (числовой) материал, который служит
для характеристики какой либо области
общественных явлений, и территориального и
временного распределения какого либо показателя.
3
Отрасль знаний, особая научная и учебная
дисциплина.
6.
ПРЕДМЕТ СТАТИСТИКИ1
Статистка изучает (получает знания, познает)
количественную сторону массовых
общественных явлений в неразрывной связи с их
качественной (содержащей) стороной, а так же
как и любая наука занимается количественным
выражением закономерностей общественного
развития (изменения) в конкретных условиях
места и времени.
о свойствах, методах, принципах,
2 Теория
закономерностях, средствах изучения
количественной стороны массовых
общественных явлений.
7.
ОБЪЕКТОМ статистики являетсяСТАТИСТИЧЕСКАЯ СОВОКУПНОСТЬ
СТАТИСТИЧЕСКАЯ СОВОКУПНОСТЬ
- это объединение социально-экономических объектов или
явления общественной жизни, соединенных качественной
связью, но отличающихся отдельными признаками (то что
отличает один предмет от другого или устанавливает
сходство).
ВИДЫ СТАТИСТИЧЕСКИХ СОВОКУПНОСТЕЙ
- Однородная – один или несколько признаков объектов
совокупности являются общими для всех ее единиц
- Неоднородная (разнородная) – совокупность, в которую
входят явления различного типа (рождаемость/смертность;
браки/разводы)
8.
Исходные понятияОБЩЕСТВЕННЫЕ ЯВЛЕНИЯ
рождаемость, смертность, болезни, брачность,
разводимость, преступность и т.д.
ОБЩЕСТВЕННЫЕ ПРОЦЕССЫ
судебные, образовательные, культурные,
экономические, демографические, транспортные,
политические
ЕДИНИЦА СОВОКУПНОСТИ
– первичный элемент который является носителем
регистрируемых (фиксируемых) признаков и основой
ведущегося при обследовании счета.
9.
ПРИЗНАКто, что один объект отличает от другого или
устанавливает сходство между ними
СТАТИСТИЧЕСКИЙ ПРИЗНАК
качественная особенность единицы совокупности.
ТИПЫ СТАТИСТИЧЕСКИХ ПРИЗНАКОВ
Количественный признак – количественное выражение (
возраст, стаж работы, средняя зарплата). Они могут быть
дискретными (точечными) или непрерывными.
• Качественный признак – имеющий содержательное
выражение (профессия, квалификация, образование). Такие
признаки называются атрибутивными (неотъемлемые
свойства предмета).
10.
ПОДТИПЫ СТАТИСТИЧЕСКИХ ПРИЗНАКОВАльтернативные признаки – когда имеются противоположные
по значению варианты признаков (лицо состоит в браке или нет,
продукция качественная/бракованная).
Пространственные (территориальные) признаки
Временные признаки
Факторные признаки (фактор – производящий, создающий;
факторы – условия, обстоятельства, следствия)
Результативные признаки – характеризуют конечные
результаты влияния факторных признаков
(количество внесенных удобрений – фактор; урожайность – результат)
Натуральный признак – натуральное выражение: тонны, литры,
килограммы, штуки
Стоимостные признаки – имеют денежное выражение
11.
СТАТИСТИЧЕСКАЯ ВАРИАЦИЯ– изменчивость признака у единиц статистической
совокупности (ЕСС)
СТАТИСТИЧЕСКИЙ ПОКАЗАТЕЛЬ
– это количественная оценка свойства изучаемого
явления, которая отражает соотношение, результат
измерения у ЕСС в целом.
ВИДЫ СТАТИСТИЧЕСКИХ ПОКАЗАТЕЛЕЙ
- Учетно-оценочные (размеры, объемы изучаемого
явления)
- Аналитические: абсолютные, относительные,
средние показатели статистических вариаций
12.
СТАТИСТИЧЕСКАЯ ЗАКОНОМЕРНОСТЬ– это форма проявления повторяемости, регулярности,
последовательности и порядка, неизменности причинноследственной связи, явлений и событий (закон – постоянство;
метод – путь).
ВИДЫ СТАТИСТИЧЕСКИХ ЗАКОНОМЕРНОСТЕЙ
Развития, изменения явлений (статистика снижения
среднего возраста вступающих в брак)
• Структурных сдвигов (структура – связи и отношения)
(увеличение доли населения преклонного возраста в сельской
местности)
• Распределения элементов совокупности (
распределение семей по численности детей)
• Установления связей между явлениями
(установление связей между себестоимостью продукции и
производительностью труда)
13.
Методы статистикиДиалектический – метод познания, согласно которому общественные
явления и процессы рассматриваются в развитии, взаимной связи и
причинной обусловленности
Метод массовых наблюдений – заключается в сборе первичного
статистического материала, в научно-организованной регистрации
ВСЕХ (каждого) существенных факторов, которые относятся к
рассматриваемому объекту, а так же регистрация отдельных признаков
и каждой единицы совокупности
Метод группировки – дает возможность все собранные с помощью
метода массовых наблюдений факты подвергнуть систематизации,
классификации, сериации (гнездовое соединение)
Метод обобщения показателей – позволяет охарактеризовать
(трактовать) изучаемые явления и процессы с помощью стат. величин
(то, чем измеряют); позволяет выявить взаимосвязи (коррялиции) и
масштабы явлений, определять закономерности развития и давать
прогнозные оценки.
Назад
14.
Статистическое исследование1. Статистическое наблюдение.
2. Сведение и группировка результатов
наблюдения.
3. Анализ и обобщение информации.
4. Построение статистических моделей.
15.
Статистическое наблюдение включает всебя следующие этапы (стадии):
1. Статистическое наблюдение, направленное на сбор
исходных данных, статистической информации и ее
первичную обработку (определить объем и виды исходной
информации, которую нужно получить)
Получение информации должно быть тщательно продумано и
четко организованно
2. Сведение (составление сводки) и группировка
результатов наблюдения.
Отметим, что при статистическом наблюдении получают
сведения о каждой единице, а сводка характеризует всю
совокупность по признакам сходства, а так же
подсчитываются суммарные показатели по группам. Данный
этап заключается в систематизации собранных данных, т.е.:
- анализ корректности и полноты данных
- представление собранной информации в удобном виде для
обработки и первичного анализа
16.
Статистическое наблюдение включает всебя следующие этапы (стадии):
3. Анализ и обобщение информации.
Данный этап связан с:
А) получением и обобщением показателей
Б) расчетам относительных и средних величин (мер,
измерений)
В) Оценка вариации и динамики показателей, а так же
балансовых построений
Г) Определение тесноты связей и роли факторов в изменении
признаков
Д) Определение материалов (количественных), которые
характеризуют итоги анализа в виде таблиц, графиков,
диаграмм, пиктограмм.
Результаты позволяют сделать соответствующие выводы и
сформулировать предложение.
17.
Статистическое наблюдение включает всебя следующие этапы (стадии):
4. Построение статистических моделей.
На данном этапе происходит исследование этих моделей, оценка
параметров, проверка гипотез, и только затем прогнозирование.
Модель – объект отражающий некоторые признаки оригинала.
Для построения статистической модели используют следующие
методы анализа:
- Факторный анализ (условия, причины, обстоятельства)
- Корреляционно-регрессивный анализ (где корреляция – установление
взаимосвязей между единицами совокупности, а регрессия – сведение к
простейшим, линейным связям между совокупностями). Данный метод
позволяет оценить тесноту и направление взаимосвязей между
результативными (прямыми и обратными) и факторными показателями;
получить уравнение зависимости результативного(у) от факторного (х),
которое может использоваться в целях прогнозирования.
18.
Статистические организацииВ Российской федерации – ГосКомСтат - единый
централизованный орган, в настоящее время РосСтат, далее имеются
региональные статистические комитеты, и т.д. до статистических
отделов.
Международные статистические организации:
1) Статистическая комиссия ООН (1964 г), ранее в 1919 году Лига
Наций проводила статистические исследования. Она проводит
регулярные сессии (форма работы этой комиссии). Данная
статистическая комиссия состоит из подразделений:
- Национальное счетоводство
- Статистика промышленности
- Статистика международной торговли
- Статистика финансов
- Статистика цен
- Статистика окружающей среды
19.
Статистические организации2) Глобальная статистическая система включает:
- Статистическую комиссию ООН
- Отраслевые статистические подразделения
- Систему стат.изданий ООН и других международных
общественных организаций
Специальные учреждения ООН:
ФАО – комиссия ООН по продовольствию
ЮНЕСКО – комиссия ООН по сотрудничеству в области науки,
культуры и образования
ВОЗ – всемирная организация здравоохранения
ВБ – всемирный банк
МВФ – международный валютный фонд
ВТО – всемирная торговая организация
3) Региональные статистические организации
Евростат – организация стран общего рынка
20.
Статистическая группировка — это процесс образованияоднородных групп на основе расчленения статистической
совокупности на части (группы, подгруппы) по существенным
для единиц этой совокупности признакам.
В экономико-статистических исследованиях применяются
группировки трех видов:
1) типологические группировки;
2) структурные группировки;
3) аналитические группировки.
21.
Типологическая группировка используется для выявления ихарактеристики социально-экономических типов явлений. Примером
такой группировки может служить деление совокупности предприятий на
части в соответствии с их формой собственности, деление экономически
активного населения региона на занятых и безработных.
Структурная группировка позволяет охарактеризовать состав явления,
процесса или совокупности.
К структурным относится группировка населения по размеру
среднедушевого дохода, группировка хозяйств по объему продукции,
структура депозитов по сроку их привлечения.
Анализ структурных группировок, взятых за ряд периодов или моментов
времени, показывает изменение структуры изучаемых явлений, т. е.
структурные сдвиги.
22.
Аналитические (факторные) группировки, в частности, исследуютсвязи и зависимости между изучаемыми явлениями и их признаками. В
основе аналитической группировки лежит факторный признак и каждая
выделенная
группа
характеризуется
средними
значениями
результативного признака. Так, группируя достаточно большое число
рабочих по факторному признаку х — квалификации (разряду) с
указанием их заработной платы, можно заметить прямую зависимость
результативного признака у — средней месячной заработной платы
рабочих от квалификации: чем выше квалификация, тем выше и средняя
месячная зарплата(хотя у отдельных рабочих с более высоким разрядом
она может быть ниже).
23.
Признак, на основе которого производится деление единицсовокупности на группы, называется группировочным
признаком.
Если группы образуются по одному признаку, то
группировка называется простой (например, деление
населения на возрастные группы). Группировка по двум или
нескольким
признакам
называется
сложной
или
комбинационной.
24.
ПРАКТИКА25.
Статистические методы26.
27.
Задача 1: Известны данные по заработной плате водителей замесяц:
Номер водителя
(табельный)
Класс водителя
% выполнения
сменных заданий
Заработная плата
за месяц (рублей)
1
I
110,2
4100,3
2
II
102,0
3600,8
3
II
111,0
3970,7
4
I
107,9
4050,2
5
II
106,4
3740,5
6
I
109,0
3985,4
7
I
115,0
4300,8
8
II
112,2
4015,7
9
I
105,0
3790,2
10
II
107,4
3700,7
11
I
112,5
4280,2
12
I
108,6
4170,1
28.
Задание: Требуется для выявления зависимостизаработной
платы
водителя
от
уровня
квалификации и процента выполнения сменных
заданий произвести аналитическую группировку
(построить таблицу).
29.
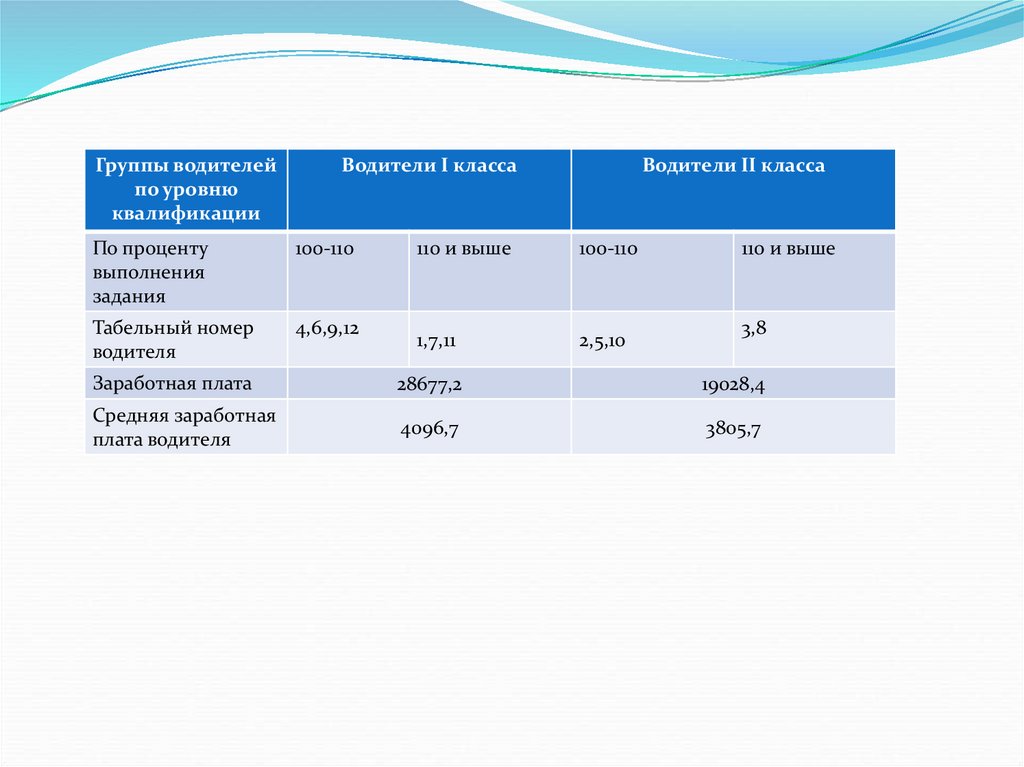
Группы водителейпо уровню
квалификации
Водители I класса
По проценту
выполнения
задания
100-110
Табельный номер
водителя
4,6,9,12
Водители II класса
110 и выше
100-110
1,7,11
2,5,10
110 и выше
3,8
Заработная плата
28677,2
19028,4
Средняя заработная
плата водителя
4096,7
3805,7
30.
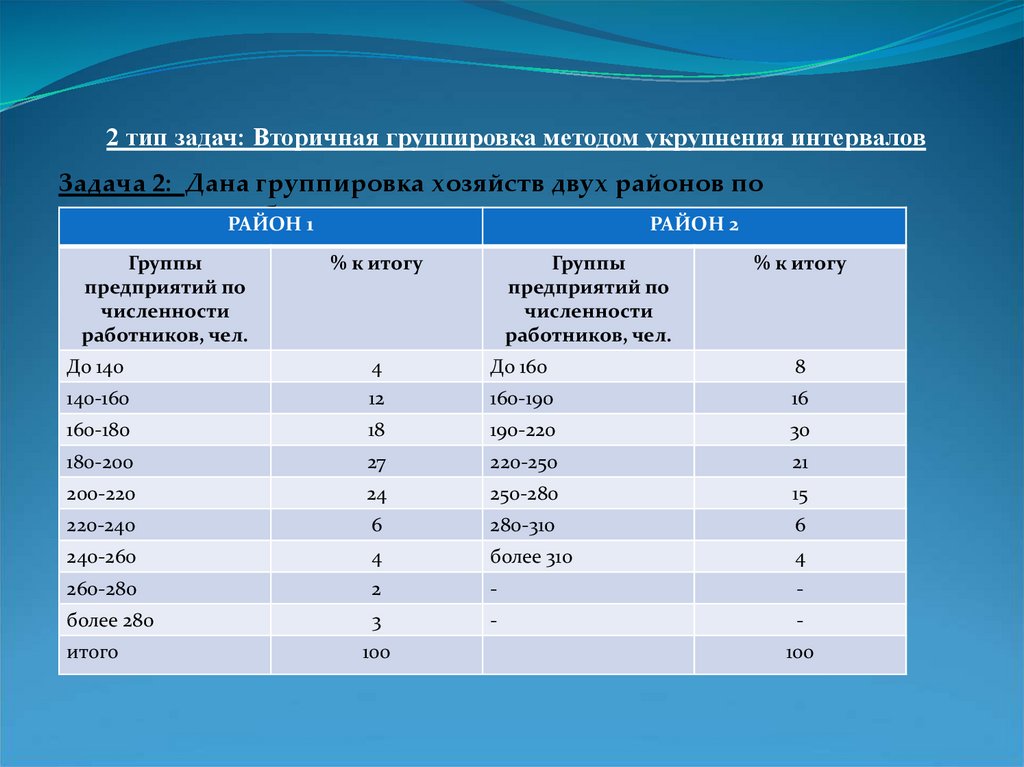
2 тип задач: Вторичная группировка методом укрупнения интерваловЗадача 2: Дана группировка хозяйств двух районов по
численности РАЙОН
работников:
1
РАЙОН 2
Группы
предприятий по
численности
работников, чел.
% к итогу
Группы
предприятий по
численности
работников, чел.
% к итогу
До 140
4
До 160
8
140-160
12
160-190
16
160-180
18
190-220
30
180-200
27
220-250
21
200-220
24
250-280
15
220-240
6
280-310
6
240-260
4
более 310
4
260-280
2
-
-
более 280
3
-
-
итого
100
100
31.
Решение:Данные группам двух районов несопоставимы, так как хозяйства распределены по группам с различными интервалами: 20 чел в
районе I и 30 чел в районе II Число выделенных групп также неодинаковое
Для приведения двух группам в сопоставимый вид проведем вторичное группировки С этой целью перегруппируют материалы в
.
группы, единые для обоих районов: возьмем интервал 40 чел
Группы хозяйств по численности
работников, чел. (новый шаг =40)
В % к итогу
1 район
2 район
До 160
4+12= 16
8
160-200
18+27= 45
10/ (220-190)=10/30=0,33
16+30*0,33=16+10=26
200-240
24+6 = 30
30-10=20
10/(250-220)=0,33
21*0,33=7
20+7=27
240-280
4+2 = 6
21-7=14
15
14+15=29
более 280
3
10
итого
100
32.
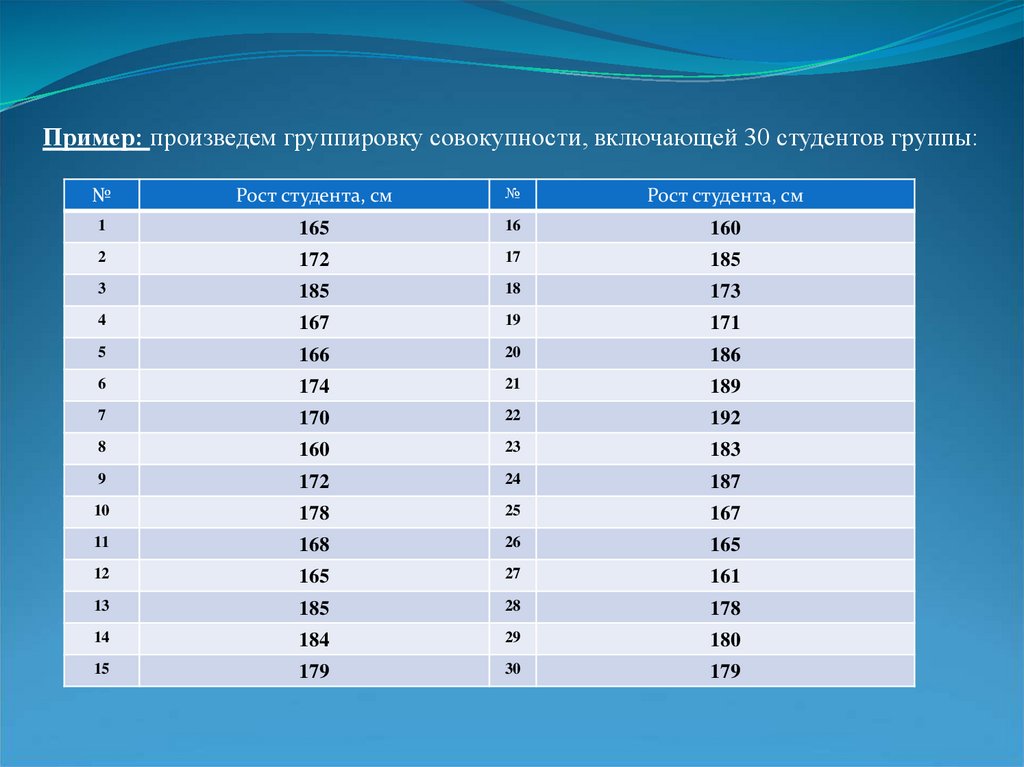
Пример: произведем группировку совокупности, включающей 30 студентов группы:№
Рост студента, см
№
Рост студента, см
1
165
16
160
2
172
17
185
3
185
18
173
4
167
19
171
5
166
20
186
6
174
21
189
7
170
22
192
8
160
23
183
9
172
24
187
10
178
25
167
11
168
26
165
12
165
27
161
13
185
28
178
14
184
29
180
15
179
30
179
33.
Вторичная группировка — образование новых групп на основеранее осуществленной группировки.
1. Определяем n (количество групп группировки) с помощью
формулы Стерджесса:
n= 1+3,322 * log30= 5,906=6;
2. Рассчитываем шаг (длину интервала группировки):
h= (Xmax – Xmin)/n, где
Xmax – максимальное значение признака,
Xmin – минимальное значение признака, т.е.
h= (192-160)/6=5,3
3. Группируем данные:
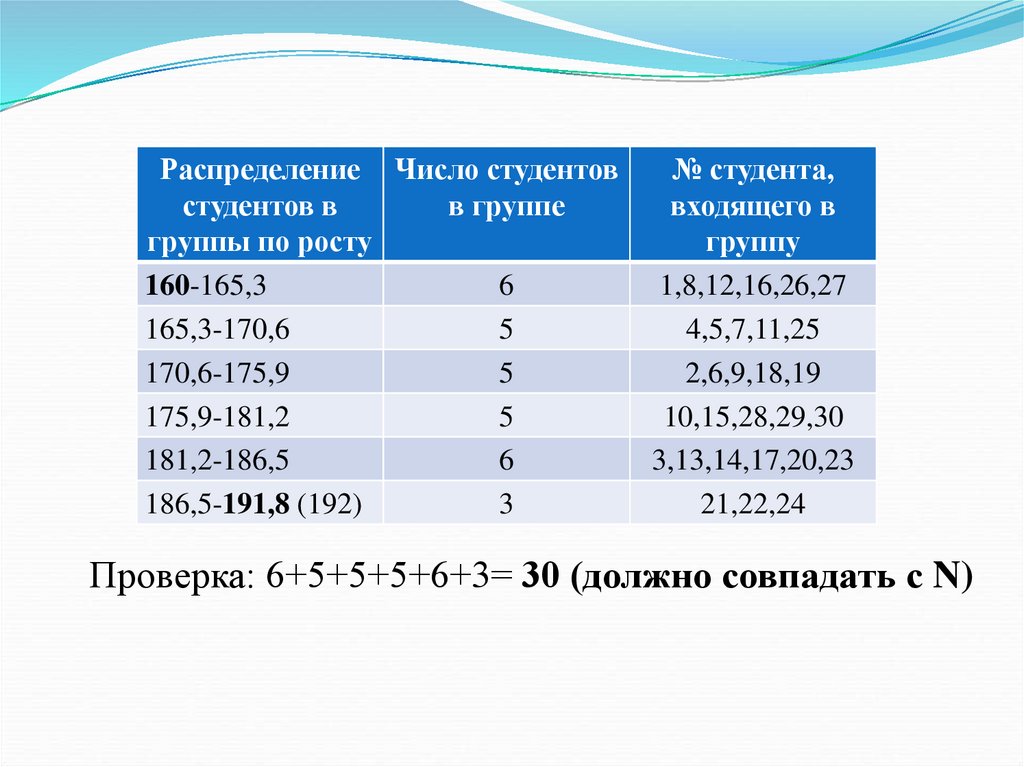
34.
Распределение Число студентовстудентов в
в группе
группы по росту
160-165,3
6
165,3-170,6
5
170,6-175,9
5
175,9-181,2
5
181,2-186,5
6
186,5-191,8 (192)
3
№ студента,
входящего в
группу
1,8,12,16,26,27
4,5,7,11,25
2,6,9,18,19
10,15,28,29,30
3,13,14,17,20,23
21,22,24
Проверка: 6+5+5+5+6+3= 30 (должно совпадать с N)
35.
Статистические ряды распределенияНесистематизированные данные, собранные в процессе стат.
наблюдения, образуют первичный ряд данных. При
достаточно большом объеме совокупности первичный ряд
данных становится трудно обозримым и непосредственное
рассмотрение его не может дать представления о
распределении единиц совокупности по величине признака.
Первым шагом в упорядочении первичного ряда является его
ранжирование, то есть расположение всех вариант ряда
(значений признака) в возрастающем или убывающем
порядке.
36.
Ранжирование данных позволяет:1) сразу увидеть максимальное и минимальное значение
признака в совокупности и оценить разницу между ними
.
2) определить число повторений отдельных вариант ряда
(частоту).
В результате первичный неупорядоченный ряд данных
преобразовывается в упорядоченный ряд, в котором будет отражено
число повторений каждой варианты:
37.
Например, стаж работы (годы) 22 рабочих бригадыхарактеризуется следующими данными:
2, 4, 5, 5, 6, 6, 5, 6, 6, 7, 7, 8, 8, 9, 10, 11, 4, 3, 3, 4, 4, 5
Ранжированный ряд:
2, 3, 3, 4, 4, 4, 4, 5, 5, 5, 5, 6, 6, 6, 6, 7, 7, 8, 8, 9, 10, 11.
Этот
ряд
называется
статистическим
рядом
распределения. Он характеризует структуру изучаемого
явления, позволяет судить о степени однородности
изучаемой совокупности, закономерности и границах
варьирования анализируемого признака.
38.
Элементами статистического ряда распределения являютсяварианты — и частоты (абсолютная величина числа повторений
i-й варианты).
Для характеристики структуры совокупности используется
показатель, который называется частостью и определяется по
формуле
39.
Из определения частоты и частости следуют равенства:;
, где N – объем совокупности.
Ряды распределения
вариационными.
могут
быть
атрибутивными
и
Атрибутивным
называется
статистический
ряд
распределения, построенный по атрибутивному признаку.
Примером атрибутивных рядов могут служить распределения
населения по занятости, национальности, профессии и т.д.
40.
Таблица – Распределение рабочих цеха по профессиямПрофессия
рабочего
Количеств
о рабочих
(частота)
Удельный вес в общей
численности рабочих
(частость)
в долях
в%
Токарь
5
0,5
50
Фрезеровщик
2
0,2
20
Слесарь
3
0,3
30
Итого
10
1,0
100
41.
Вариационным называется статистический рядраспределения, построенный по количественному
признаку. Вариационный ряд является дискретным,
если признак, по которому он построен — дискретный,
и интервальным, если признак, по которому он
построен — непрерывный.
Примером дискретного ряда может служить распределение
рабочих предприятия по квалификации:
42.
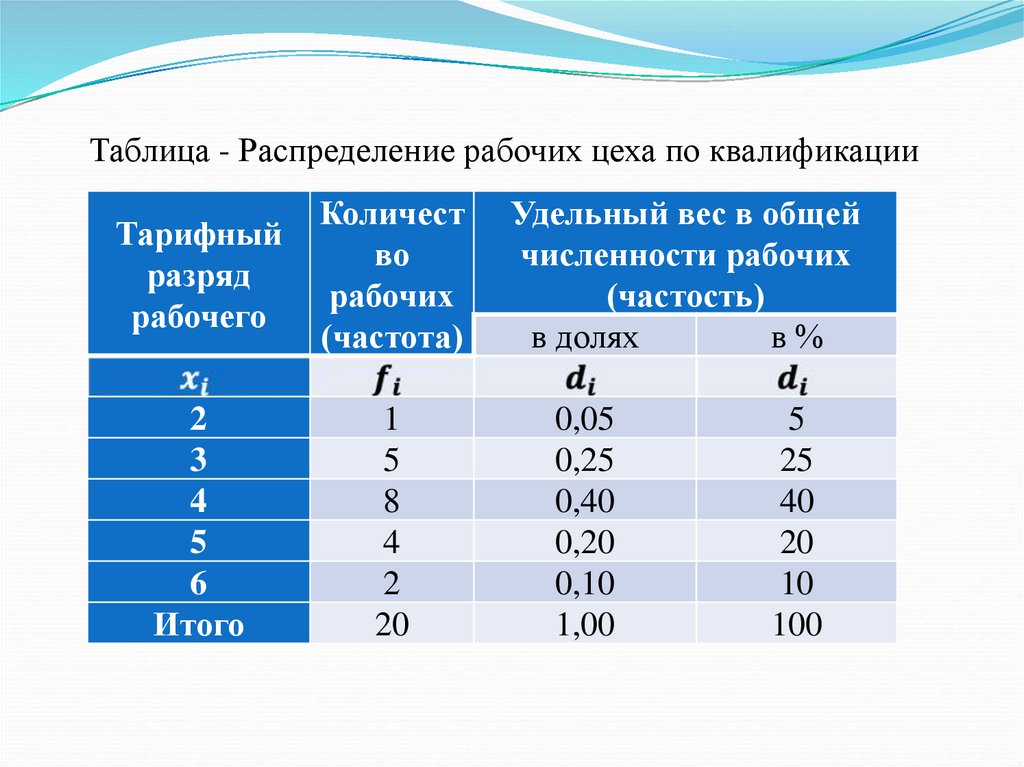
Таблица - Распределение рабочих цеха по квалификацииТарифный
разряд
рабочего
Количест
во
рабочих
(частота)
2
3
4
5
6
Итого
1
5
8
4
2
20
Удельный вес в общей
численности рабочих
(частость)
в долях
в%
0,05
0,25
0,40
0,20
0,10
1,00
5
25
40
20
10
100
43.
Данные табл.характеризуют структуру рабочих по
квалификации. Наличие такой информации за несколько
периодов дает возможность судить о динамике этой
структуры, позволяя оценивать изменение качества рабочей
силы.
Примером интервального ряда распределения является
распределение предприятий по объему произведенной
продукции,
выполненное
в
процессе
построения
соответствующей аналитической группировки.
44.
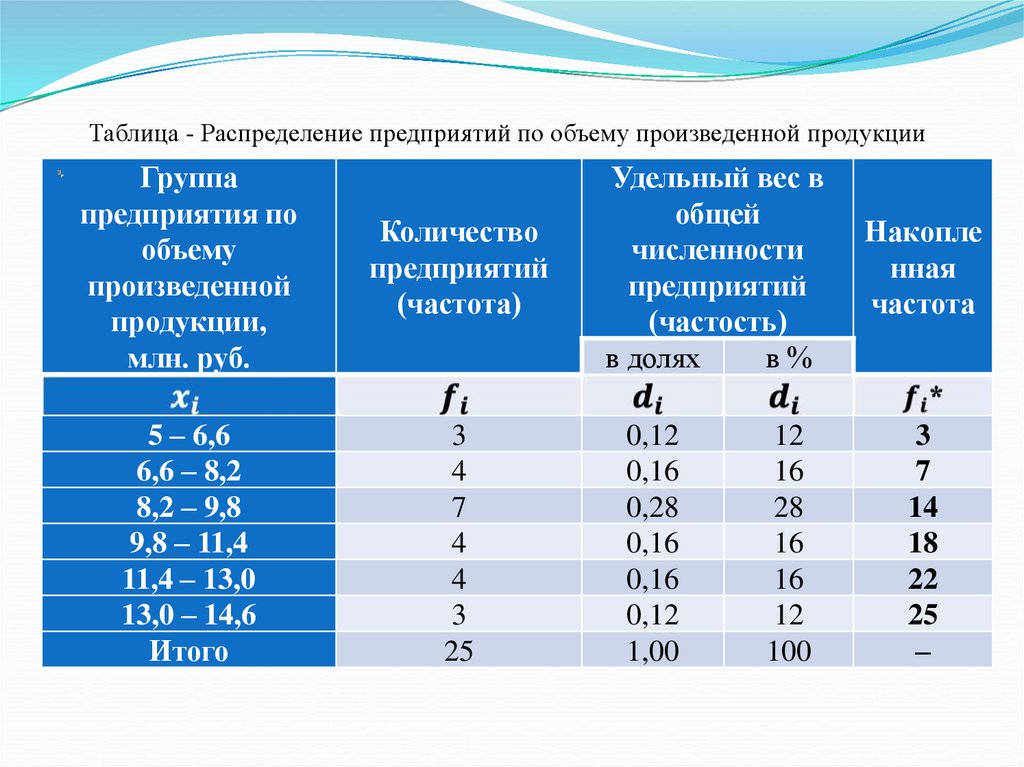
Таблица - Распределение предприятий по объему произведенной продукцииГруппа
предприятия по
объему
произведенной
продукции,
млн. руб.
Количество
предприятий
(частота)
5 – 6,6
6,6 – 8,2
8,2 – 9,8
9,8 – 11,4
11,4 – 13,0
13,0 – 14,6
Итого
3
4
7
4
4
3
25
Удельный вес в
общей
численности
предприятий
(частость)
в долях
в%
0,12
0,16
0,28
0,16
0,16
0,12
1,00
12
16
28
16
16
12
100
Накопле
нная
частота
3
7
14
18
22
25
–
45.
Статистический ряд распределения является обязательным итогом любойгруппировки.
Стат. ряды распределения могут быть изображены графически. Чаще всего
графики используют для изображения вариационных стат. рядов.
Дискретный ряд изображают с помощью линейной диаграммы, которая
называется полигоном распределения. При построении его в
прямоугольной системе координат по оси абсцисс откладываются варианты
(значения анализируемого признака), а по оси ординат — частота или
частость. Целесообразнее по оси ординат откладывать частости: во-первых,
это удобнее при большом объеме совокупности, а во-вторых, это позволяет
на одном графике изображать статистические ряды распределения
нескольких признаков с разным числом единиц совокупности. Полученные
на пересечении абсцисс и ординат точки соединяют прямыми линиями, в
результате чего получают ломаную линию, называемую полигоном
распределения.
46.
На рис. представлен полигон распределения,построенный по данным табл. «Распределение рабочих
цеха по квалификации»
47.
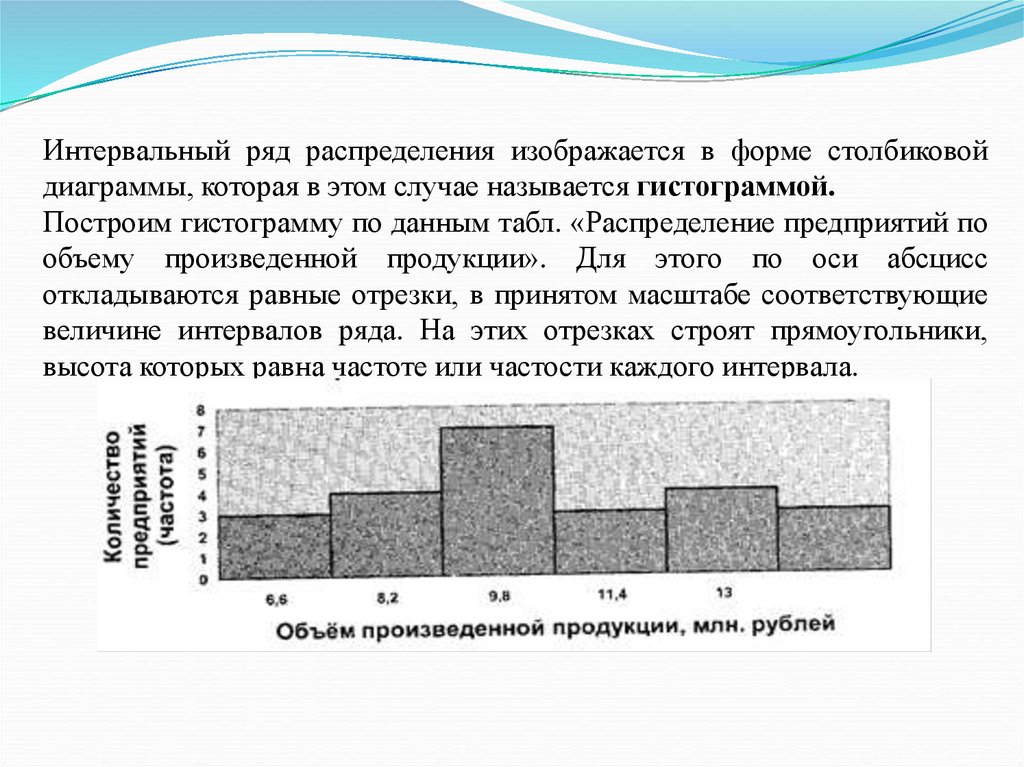
Интервальный ряд распределения изображается в форме столбиковойдиаграммы, которая в этом случае называется гистограммой.
Построим гистограмму по данным табл. «Распределение предприятий по
объему произведенной продукции». Для этого по оси абсцисс
откладываются равные отрезки, в принятом масштабе соответствующие
величине интервалов ряда. На этих отрезках строят прямоугольники,
высота которых равна частоте или частости каждого интервала.
48.
Для решения ряда задач (определение структурныхсредних, наблюдение за процессом концентрации
изучаемого
явления)
ряды
распределения
преобразовывают в кумулятивные ряды, строящиеся
по накопленным частотам или частостям.
Накопленные частоты (частости) каждого интервала
ряда распределения рассчитываются как сумма
частоты (частости) этого интервала и частот
(частостей)
всех
интервалов,
которые
ему
предшествуют.
49.
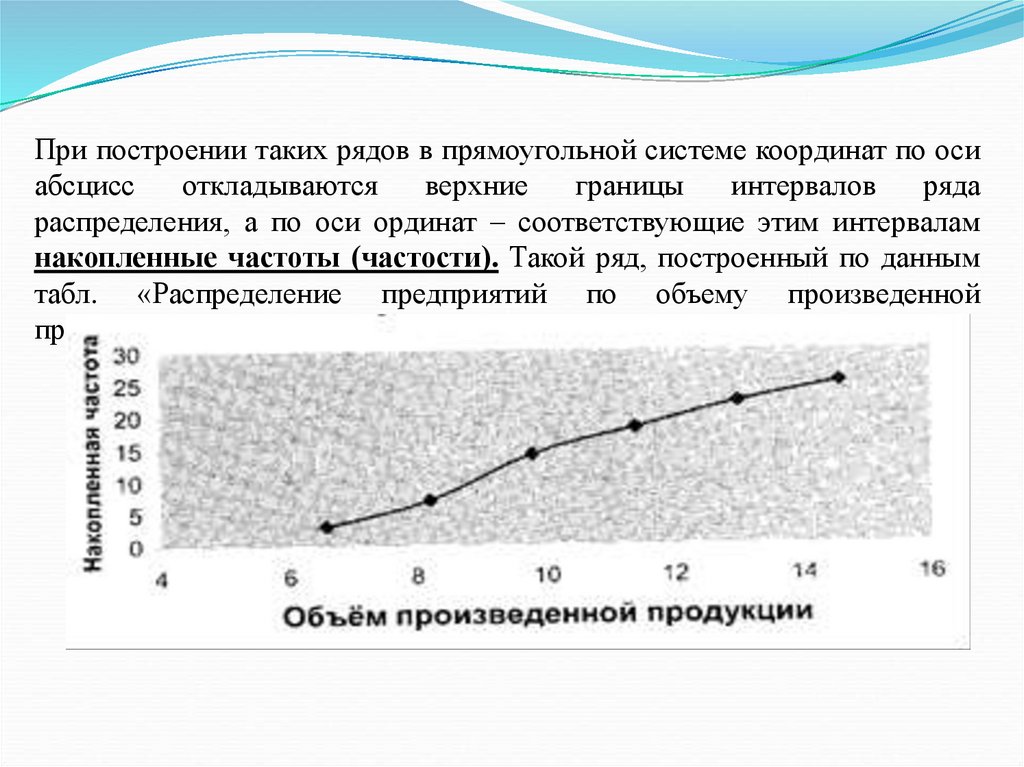
При построении таких рядов в прямоугольной системе координат по осиабсцисс
откладываются
верхние
границы
интервалов
ряда
распределения, а по оси ординат – соответствующие этим интервалам
накопленные частоты (частости). Такой ряд, построенный по данным
табл. «Распределение предприятий по объему произведенной
продукции».
50.
С помощью кумулятивных кривых можно иллюстрироватьпроцесс концентрации, если наряду с накопленными
частотами (или частостями) иметь в статистическом ряду
распределения суммы накопленных группировочных и других
важных признаков изучаемого явления.
Так, в приведенном примере, накопленная частота, например,
второго интервала свидетельствует, что 7 предприятий (28%
их общей численности), имеющие каждый объем
произведенной продукции не более чем 8,2 млн. рублей,
производят только 19% всей продукции по совокупности.
51.
Одним из важнейших требований, предъявляемых кстатистическим
рядам
распределения,
является
сопоставимость во времени и в пространстве отдельных
интервалов. В рядах с равными интервалами это требование
выполняется «автоматически».
Для обеспечения выполнения сопоставимости статистических
рядов с неравными интервалами рассчитывается плотность
распределения, представляющая собой частное от деления
частоты интервала на его длину. При графическом изображении
таких рядов по оси ординат вместо частот (частостей)
откладываются значения плотности распределения.
52.
Существует множество графических изображений. В основу ихклассификации может быть положен ряд признаков: а) способ построения
графического образа; б) геометрические знаки, изображающие статистические
показатели и отношения; в) задачи, решаемые с помощью графического
изображения.
По способу построения статистические графики делятся на диаграммы и
статистические карты. Диаграммы - наиболее распространенный способ
графических изображений. Диаграммы применяются для наглядного
сопоставления в различных аспектах (пространственном, временном и др.)
независимых друг от друга величин: территорий, населения и т.д. При этом
сравнение исследуемых совокупностей производится по какому-либо
существенному варьирующему признаку. Статистические карты - графики
количественного распределения по поверхности. Они представляют собой
условные изображения статистических данных на контурной географической
карте, то есть показывают пространственное размещение и пространственную
распространенность статистических данных.
53.
Геометрические знаки - это либо точки, либо линии илиплоскости, либо геометрические тела. В соответствии с
этим, различают графики точечные, линейные, плоскостные
и пространственные (объемные).
При построении точечных диаграмм в качестве графических
изображений применяются совокупности точек; при
построении линейных - применяются линии.
54.
Диаграммы сравненияДиаграммы сравнения применяются для графического отображения статистических
данных с целью их наглядного сопоставления друг с другом в тех или иных разрезах.
Сравнительные диаграммы делятся на:
а) диаграммы простого сопоставления;
б)структурные диаграммы;
в) изобразительные (фигур-знаков).
Диаграммы простого сопоставления дают наглядную сравнительную характеристику
статистических совокупностей по какому-либо варьирующему признаку. При этом
сопоставляемые совокупности и их части классифицируются по какому-либо атрибутивному
или количественному признаку так, что отражаемый диаграммой статистический ряд
представляет собой дискретный ряд цифр, на основе которого и строится график.
55.
Диаграммы простого coпоставления делятся на полосовые истолбиковые. Основной особенностью этих диаграмм является
одномерность графического выражения величин варьирующего
признака и их одномасштабность для различных столбцов или полос,
характеризующих величину отражаемого признака в разных
классификационных группах.
На столбиковых диаграммах статистические данные изображаются в
виде вытянутых по вертикали прямоугольников. Построение
столбиковой диаграммы требует применения вертикальной масштабной
шкалы. Основания столбиков размещаются на горизонтальной линии, а
высота столбиков устанавливается пропорционально изображаемым
величинам.
56.
Полосовые диаграммы состоят из прямоугольников, расположенныхгоризонтально. В этом случае масштабная шкала - горизонтальная ось.
Принцип их построения тот же, что и в столбиковых.
Для сопоставления изменяющихся во времени показателей, а также
при сравнении величин, относящихся к одному и тому же периоду,
могут использоваться квадратные и круговые диаграммы. В отличие
от столбиковых или полосовых диаграмм они выражают величину
изображаемого явления размером своей площади. Чтобы изобразить
квадратную диаграмму, необходимо из сравниваемых статистических
величин извлечь квадратные корни, а затем построить квадраты со
сторонами, пропорциональными полученным результатам. Круговые
диаграммы строятся аналогично. Разница состоит лишь в том, что на
графике вычерчиваются круги, радиусы которых пропорциональны
квадратному корню из изображаемых величин.
57.
Диаграммы структуры это такие диаграммы, в которых отдельныестатистические совокупности сопоставляются по их структуре, характеризующейся
соотношением разных параметров совокупности или ее отдельных частей.
Простейшим видом структурных статистических диаграмм являются диаграммы
удельных весов, отражающие структуры сравниваемых совокупностей по
процентному соотношению в них отдельных частей, выделяемых по тому или иному
количественному или атрибутивному признаку. Эти диаграммы получены путем
преобразования простой полосовой диаграммы с подразделенными полосами.
Другой широко распространенный метод графического изображения структур
статистических совокупностей по соотношению удельных весов заключается в
составлении структурных круговых или секторных диаграмм. Секторные диаграммы
удобно строить следующим образом: вся величина явления принимается за сто
процентов, рассчитываются доли отдельных частей в процентах. Круг разбивается на
секторы пропорционально частям изображаемого целого. Таким образом, на 1%
приходятся 3,6 градуса. Для получения центральных углов секторов, изображающих
доли частей целого, необходимо их процентное выражение умножить на 3,6 градуса.
58.
Секторные диаграммы выглядят убедительно при существенныхразличиях сравниваемых структур, а при небольших различиях они
могут быть недостаточно выразительны. Значительным преимуществом
столбиковых структурных диаграмм по сравнению с секторными
является их большая емкость, возможность отразить на небольшом
пространстве большой объем полезной информации.
Для одновременного изображения трех величин, связанных между
собой таким образом, что одна величина является произведением двух
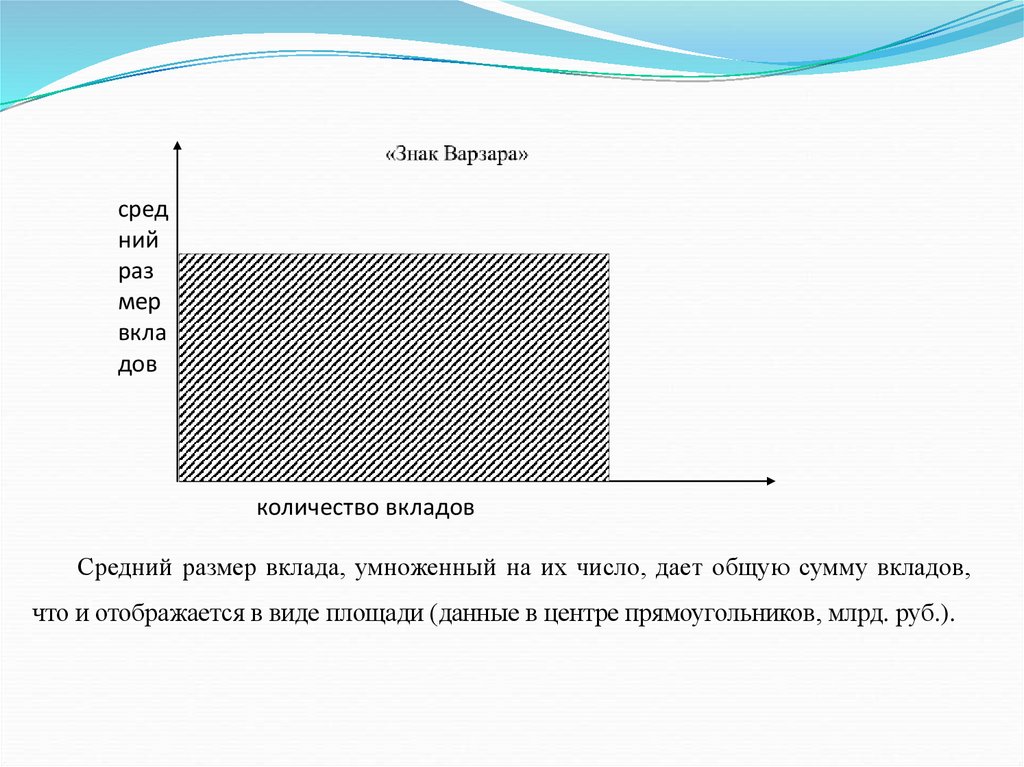
других, применяются диаграммы, называющиеся «знаком Варзара».
«Знак Варзара» представляет собой прямоугольник, у которого один
сомножитель принят за основание, другой за высоту, а вся площадь
равна произведению.
Оба показателя откладываются на шкалах (каждый на своей), третий
(результат) изображается в виде прямоугольника в поле графика.
59.
средний
раз
мер
вкла
дов
количество вкладов
Средний размер вклада, умноженный на их число, дает общую сумму вкладов,
что и отображается в виде площади (данные в центре прямоугольников, млрд. руб.).
60.
Для изображения и внесения суждений о развитии явления во времени строятсядиаграммы динамики. В рядах динамики используются для наглядного
изображения явлений многие диаграммы: столбиковые, ленточные, квадратные,
круговые, линейные, радиальные и другие. Выбор вида диаграмм зависит в
основном от особенностей исходных данных, от цели исследования.
Например, если имеется ряд динамики с несколькими неравноотстоящими
уровнями во времени (1913, 1940, 1950, 1980,1985, 1995), то часто для наглядности
используют столбиковые, квадратные или круговые диаграммы. Они зрительно
впечатляют, хорошо запоминаются, но не годны для изображения большого числа
уровней, так как громоздки, и если число уровней в ряду динамики велико, то
целесообразно применять линейные диаграммы, которые воспроизводят
непрерывность процесса развития в виде непрерывной ломаной линии. Кроме того,
линейные диаграммы удобно использовать: когда целью исследования является
изображение общей тенденции и характера развития явления; когда на одном
графике необходимо изобразить несколько динамических рядов с целью их
сравнения; когда наиболее существенным является сопоставление темпов роста, а не
уровней.
61.
К диаграммам динамики относятся и радиальныедиаграммы, построенные в полярных координатах и
предназначенные для отражения процессов,
ритмически повторяющихся во времени. Чаще всего
эти диаграммы применяются для иллюстрации
сезонных колебаний, и в этом отношении они имеют
преимущество перед статистическими кривыми.
62.
Месячное потребление электроэнергии63.
Задание:ПРИДУМАТЬ И ОТОБРАЗИТЬ ГРАФИЧЕСКИ
3 ПРИМЕРА
НА ОСНОВЕ СТАТ.ДАННЫХ
64.
Лекция №21. Понятие статистического наблюдения
2. Методология статистического наблюдения
3. Организационные вопросы наблюдения
4. Формы статистического наблюдения
5. Виды статистического наблюдения
6. Вопросы точности наблюдения
7. Программа наблюдения
8. Инструкция
65.
Понятие статистическогонаблюдения
1. Статистическое наблюдение
2. Особенности статистического наблюдения
3. Требования к наблюдению
66.
Статистическое наблюдение- это (первая стадия статистического
исследования) мероприятие включающее:
А) Научно-организованную по единой
программе регистрацию(фиксацию)
отобранных признаков и фактов у каждой
единицы совокупности
Б) Учет факторов (условий, причинных
обстоятельств и т.д.), которые характеризуют
явления и процессы общественной жизни
В) Сбор данных полученных на основе
регистрации и учета обстоятельств
67.
Особенности статистического наблюдения- Массовость
- Систематичность, периодичность проведения
наблюдений
- Планомерность: наблюдение готовится и
проводится по плану, включающему вопросы:
+методологии организации;
+ технике сбора информации
+ контроля качества собранного материала
+ достоверности и оформления итоговых
результатов (графики, таблицы)
68.
Требования к статистическому наблюдению- Полнота статистических данных (всех
достаточно, но каждый необходим)
Достоверность, точность, единообразие и
сопоставимость данных
69.
МЕТОДОЛОГИЯ СТАТИСТИЧЕСКОГО НАБЛЮДЕНИЯЦель наблюдения – сбор достоверной информации о
социально-экономических явлениях, процессах, для выявления
закономерностей развития явлений и процессов.
Объект наблюдения – статистическая совокупность.
Установить объект значит точно определить состав и границы
статистической совокупности.
Единица наблюдения – то, что подлежит регистрации
(человек, семья и т.д.)
Отчетная единица – субъект от которого поступают данные об
единице наблюдения (организация, ферма, семья, человек и т.д.)
Программа наблюдения (проект) – представляет собой
перечень вопросов на которые следует получить ответ в процессе
наблюдения. Данные вопросы необходимы для решения
поставленной цели. Т.е. эти вопросы – задачи (как
мероприятие).
70.
ОРГАНИЗАЦИОННЫЕ ВОПРОСЫ НАБЛЮДЕНИЯСвязанны с выбором места, времени, формы, способа, субъекта.
1. Определить субъект наблюдения – значит установить какой
орган будет осуществлять наблюдение (органы статистики;
кадровые работники; другие специалисты), т.е. тот, кто будет
производить наблюдение. Субъект – носитель деятельности.
2. При установлении времени наблюдения определяют либо
период (срок наблюдения), либо время к которому относятся
регистрируемые сведения (момент времени – объективное время
наблюдения, которое называют критическим моментом
наблюдения).
3. Место наблюдения – где нужно проводить регистрацию
данных, заполнение формуляра наблюдения.
Место наблюдения имеет важную роль. Существуют особые
места куда надо явится, что бы сообщить о себе сведения (ЗАГС,
УФМС).
71.
ОРГАНИЗАЦИОННЫЕ ВОПРОСЫ НАБЛЮДЕНИЯ4. Организационный план наблюдения (документ) – кроме указания в
плане цели, единицы, места, времени, органа наблюдения, программы
наблюдения, в организационном плане перечисляются подготовительные
мероприятия. К подготовительным мероприятиям относятся:
Подбор и обучение кадров привлекаемых к наблюдению
Составление списков единиц наблюдения
Подготовка картографического материала (анкеты, бланки, формуляры)
Разбивка территории на части, в которых наблюдение поручается различным
лицам
Определение местонахождения работников различных рангов,
осуществляющих наблюдения.
Ясно, что в организационном плане должны быть указаны ответственные
лица, порядок и сроки, порядок выполнения, статистический
инструментарий, транспортные средства.
5. Немаловажный вопрос наблюдения РАЗЪЯСНЕНИЕ НАСЕЛЕНИЮ
целей, задач, порядок проведения через плакаты, брошюры, буклеты, СМИ.
72.
Формы статистическогонаблюдения
1. Отчетность
2. Перепись
3. Опрос
4. Документальный способ
5. Единовременный учет
6. Способ непосредственного наблюдения
7. Регистры
73.
Статистическая отчетностьОсновная форма статистического наблюдения, которая
заключается в получении статистическими органами данных
от единиц наблюдения. Данные поступают в органы
статистики от предприятий и организаций в виде
обязательных отчетов об их деятельности. Отчётные
документы утверждаются Министерством финансов РФ и
Госкомстатом РФ. Методы и формы организации
статистической
отчетности
дифференцируются
применительно к различным типам предприятий и формам
предпринимательства. Основными формами ответности
являются бухгалтерский баланс и отчет о прибылях и
убытках.
74.
Статистическая отчетностьПо видам статистическая отчетность бывает:
А) По срокам:
- ежедневная
- недельная
- месячная
- квартальная
- годовая
-Текущая
Б) По способу
представления:
-факс
-почта
-е-майл
75.
Перепись- это наблюдение, которое повторяется через
равные промежутки времени, с целью получения
сведений о численности, составе, и состоянии
объекта статистического наблюдения по ряду
признаков.
Виды переписи:
- Населения
- Материальных ресурсов
- Оборудования
- Строек
-незавершенного строительства и
т.д.
Требования:
1. Одновременность на всей
территории
2. Единство программ
3. Регистрация всех единиц на
один и тот же критический момент
времени (дату)
76.
ОпросЭто источник сведений, при котором наблюдаемые
сведения получаются со слов респондента.
Документальный способ
Основан на использовании в качестве источника
сведений различного рода документы учетного
характера.
Единовременный учет
Установление наличия количества чего-нибудь путем
подсчета в определенный момент времени наблюдения
77.
Способ непосредственного наблюденияРегистраторы (лица, проводящие наблюдение)
путем непосредственного замера, взвешивания,
подсчета, проверки работы (ввод в
эксплуатацию жилых домов) устанавливают
факт подлежащий регистрации, и на этом
основании производят записи в формуляре
наблюдения.
78.
Регистры-Это форма непрерывного статистического наблюдения за
долговременными процессами, имеющими фиксированное
начало, стадию развития и фиксированный конец.
Регистр – система, постоянно следящая за состоянием
единиц наблюдения и оценивающая силу воздействия
различных факторов на изучаемые показатели. В регистре
каждая единица наблюдения характеризуется совокупностью
показателей. Эти показатели могут быть: неизменными,
обновляемыми по мере изменения.
ЕГРПО – единый государственный регистр предприятий и
организаций (всех форм собственности: частная,
государственная, муниципальная). Был организован в 1993
году.
79.
Виды регистров- Регистр населения – перечень жителей страны (пол,
дата и место рождения, дата вступления в брак, брачное
состояние) – это регулярно актуализируемый регистр
(ЗАГС)
- Регистр предприятий – содержит данные о времени
создания, регистрации предприятия, его название,
адрес, телефон, структуру, вид эк. Деятельности,
количество занятых и т.д.
80.
Виды статистического наблюденияСуществуют виды наблюдений:
1. По временному признаку
2. По охвату объема единиц наблюдения
3. По способу регистрации данных
статистического наблюдения
81.
Виды статистического наблюдения повремени регистрации:
•Текущее (непрерывное) наблюдение - проводится для
изучения текущих явлений и процессов. Регистрация фактов
осуществляется по мере их свершения. (регистрация
семейных браков и разводов)
•Прерывное наблюдение — проводится по мере
необходимости, при этом допускаются временные разрывы в
регистрации данных:
•Периодическое наблюдение — проводится через
сравнительно равные интервалы времени (перепись
населения).
•Единовременное наблюдение — осуществляется без
соблюдения строгой периодичности его проведения.
82.
Виды статистического наблюдения пополноте охвата единиц совокупности:
- Сплошное – полный учет всех единиц изучаемой
совокупности
- Не сплошное – учет части единиц совокупности, на основе
которого можно получить обобщающую характеристику
всей совокупности
Данные должны соответствовать одному циклу
изучаемого процесса (учебный год, финансовый год). На
достоверность оказывает влияние сезонность (месяц,
квартал), когда наблюдаемый объект находится в наиболее
стабильном состоянии.
83.
Несплошное наблюдение подразделяется на:•Выборочное наблюдение - основано на случайном отборе
единиц, которые подвергаются наблюдению.
•Монографическое наблюдение — заключается в обследовании
отдельных единиц совокупности, характеризующихся редкими
качественными свойствами. Пример монографического
наблюдения: характеристика работы отдельных предприятий, для
выявления недостатков в работе или тенденций развития.
•Метод основного массива — состоит в изучении самых
существенных, наиболее крупных единиц совокупности, имеющих
по основному признаку наибольший удельный вес в изучаемой
совокупности.
•Метод моментных наблюдений — заключается в проведении
наблюдений через случайные или постоянные интервалы времени с
отметками о состоянии исследуемого объекта в тот или иной
момент времени.
84.
По способу регистрации стат.данныхнаблюдение подразделяется на:
Экспедиционный — регистраторы получают необходимую информацию
от опрашиваемых лиц и сами фиксируют ее в формулярах.
Способ саморегистрации — формуляры заполняются самими
респондентами, регистраторы только раздают бланки и объясняют
правила их заполнения.
Корреспондентский — сведения в соответствующие органы сообщает
штат добровольных корреспондентов.
Анкетный — сбор информации осуществляется в виде анкет,
представляющих собой специальные вопросники, удобен в случаях, когда
не требуется высокая точность результатов.
Явочный — заключается в предоставлении сведений в соответствующие
органы в явочном порядке.
85.
Вопросы точности наблюдения1. Точность статистического наблюдения
2. Достоверность
3. Сопоставимость данных
4. Ошибка наблюдения
5. Источники ошибок
6. Виды ошибок
7. Контроль статистического материала
86.
Вопросы точности наблюденияТочность статистического наблюдения
- Это степень соответствия величины какого либо
показателя,
определяемого
(вычисляемого
по
материалам стат.наблюдения, действительной величине,
значению).
Точность
определяется
отношением
(делением) или разностью вычисляемых величин и
вычисленных значений.
87.
Достоверность-Это соответствие тому, что есть на самом деле.
Условиями обеспечения достоверности являются:
полнота охвата наблюдаемого объекта;
полнота и точность регистрации данных
(сведений) по каждой единице наблюдения
88.
Сопоставимость данныхЧтобы данные о отдельных ед.наблюдения можно было
обобщать, они должны быть сопоставимы с друг другом
– собираться в одно и то же время по одной методике.
Должна быть возможность сравнивать их с прошлыми
исследованиями, чтобы понять, как изменяются данные,
характер и причины различий данных наблюдений.
89.
Ошибка наблюденияЭто погрешность, расхождение между расчетными и
действительными значениями изучаемых величин. Они
являются следствием неточности при подсчете, расчете,
регистрации, значений изучаемых признаков
Источники ошибок наблюдения:
1. Плохая подготовка кадров
2. Нечеткое определение объекта наблюдения или единицы
совокупности наблюдения
3. Недостатки составления программы (плохие вопросы)
Для профилактики необходимо:
- проводить контрольные проверки
- повторное наблюдение
- требовать документы которые подтверждают
регистрируемые факты
90.
Виды ошибок наблюдения:1. Ошибки регистрации – они бывают:
А) случайные, непреднамеренные – возникают в следствии случайных
причин, например оговорка опрашиваемого, ослышался регистратор,
переставил цифры при записи (27-72 возраст)
Б) Систематические (тенденционные, намеренные) – возникают под
действием определенных причин (округление цифр, сознательное
искажение фактов финансовой отчетности).
2. Ошибки представительности (ошибки репрезентативности) –
отклонение величины изучаемого признака в отобранной части
совокупности от его значения по всей совокупности. Данные ошибки
свойственны только для не сплошного наблюдения.
А) Случайные – возникают в силу не полного воспроизведения признака
совокупности в целом. Эти ошибки могут быть оценены математически
Б) Систематические – Нарушение принципа случайности отбора
единиц совокупности (т.е. преднамеренный отбор, такие ошибки не
поддаются количественной оценке).
91.
Контроль статистического материала:1. Контроль полноты - проверка того, на сколько полно
охвачен объект наблюдения, т.е. о всех ли единицах наблюдения
собраны сведения
2. Контроль качества – проверка качества заполнения
формуляров и других документов наблюдения. Данный вид
подразделяется на:
А) Арифметический контроль – т.е. счетные проверки
итогов, вычисление процентов расчетов средних величин,
сопоставление показателей, которые взаимосвязаны
(наблюдение в 2000 году: год рождения – 1925, возраст – 50 лет, а
должно быть 75)
Б) Логический контроль состоит в сопоставлении ответов на
взаимосвязанные между собой вопросы программы наблюдения
с целью выявления логически несовместимых ответов.
92.
Программа статистического наблюденияОна включает в себя:
1. Перечень признаков, подлежащих регистрации в процессе
наблюдения
2. Перечень вопросов, на которые следует получить ответ в
процессе наблюдения
Должна отвечать следующим требованиям:
•Программа должна содержать существенные признаки
непосредственно характеризующие изучаемые явления.
•В программу не следует включать второстепенные вопросы,
которые затрудняют работу по сбору информации, ее обработке и
анализу.
•В программу следует включать вопросы контрольного характера,
служащие целям проверки и уточнения информации.
93.
Программа статистического наблюденияДля записи ответов на вопросы программы
наблюдения разрабатывается формуляр наблюдения.
Формуляр наблюдения — это особым сформированный
бланк, в котором содержатся перечень вопросов программы.
Статистический формуляр должен быть удобен для чтения,
записи и обработки. К формулярам составляется инструкция,
где подробно разъясняется, как следует заполнить
статистический формуляр.
В процессе статистического наблюдения собирается
первичная информация, которая затем подвергается
систематизации обобщению и анализу.
94.
Программа статистического наблюденияОт качества первичной информации зависит успех всего
исследования, поэтому к информации предъявляется ряд
требований:
1. Достоверность — это соответствие тому, что есть на самом
деле.
Достоверность зависит от:
Статиста — профессиональная подготовка, организационные
навыки, добросовестность.
Качества инструментария наблюдения — программа
наблюдения, формуляр, инструкция по заполнению.
2. Сопоставимость - сравнимость данных с прошлыми
исследованиями. Сопоставимость обеспечивается
использованием одних и тех же единиц измерения,
наблюдением в одно и тоже время и по единой методологии.
95.
ИнструкцияИнструкция- это совокупность разъяснений, и
указаний по программе (по вопросам) наблюдений
Инструкция может быть представлена в виде: документа
(брошюры) или приведенного практического примера.
Инструкцию следует писать: кратко, просто, пояснения и
указания должны быть ясными и четкими.
В инструкции должны быть указаны:
- цель проведения наблюдения
- что подлежит наблюдению (объект и ед.наблюдения)
- время наблюдения
- кто проводит наблюдение
96.
ИнструкцияОсобое место в инструкции отводиться:
- разъяснению вопросов содержащихся в формуляре
наблюдения
- как следует записывать в нем ответ на тот или иной вопрос
-на основании чего (источник сведений) записывается ответ
Иногда в формуляре после вопросов, сразу же даются
варианты возможных ответов – статистический подсказок.
Статистические подсказки бывают:
- полный подсказ – если перечень возможных ответов
исчерпывающий
- неполный подсказ – если указываются только некоторые из
возможных ответов.
ИТОГ: Совокупность документов применяемых при
статистическом наблюдении представляет собой
СТАТИСТИЧЕСКИЙ ИНСТРУМЕНТАРИЙ.
97.
ПРАКТИКА98.
Тема: Средние величиныСредняя величина — это обобщающая мера
варьирующего признака, которая характеризует его
уровень в расчете на единицу совокупности.
Средние величины рассчитываются на основе
данных правильно организованного статистического
наблюдения, а условиями их применения является
наличие качественно однородной совокупности и
достаточно большой ее объем.
99.
Наиболее часто в экономико-статистических исследованияхиспользуется средняя арифметическая. Она применяется в том
случае, когда объем изучаемого признака образуется как сумма
значений отдельных единиц анализируемой совокупности.
Средняя арифметическая может быть простой и взвешенной.
Простая средняя
следующей формуле:
арифметическая
рассчитывается
x1 x2 ... xn x
xар
n
n
где x1, x2, …, xn – индивидуальные значения
варьирующего признака (варианты);
п – число единиц совокупности
по
100.
Средняя из вариантов, которые повторяются различное числораз, или имеют различный вес, называется взвешенной. В
качестве весов выступают численности единиц в разных группах
совокупности (в группу объединяют одинаковые варианты).
x1 f1 x2 f 2 ... xn f n xf
xар
f1 f 2 ... f n
f
где f1 , f 2 ,..., f n – веса (частоты повторения одинаковых признаков);
xf – сумма произведений величины признаков на их частоты;
x – общая численность единиц совокупности.
101.
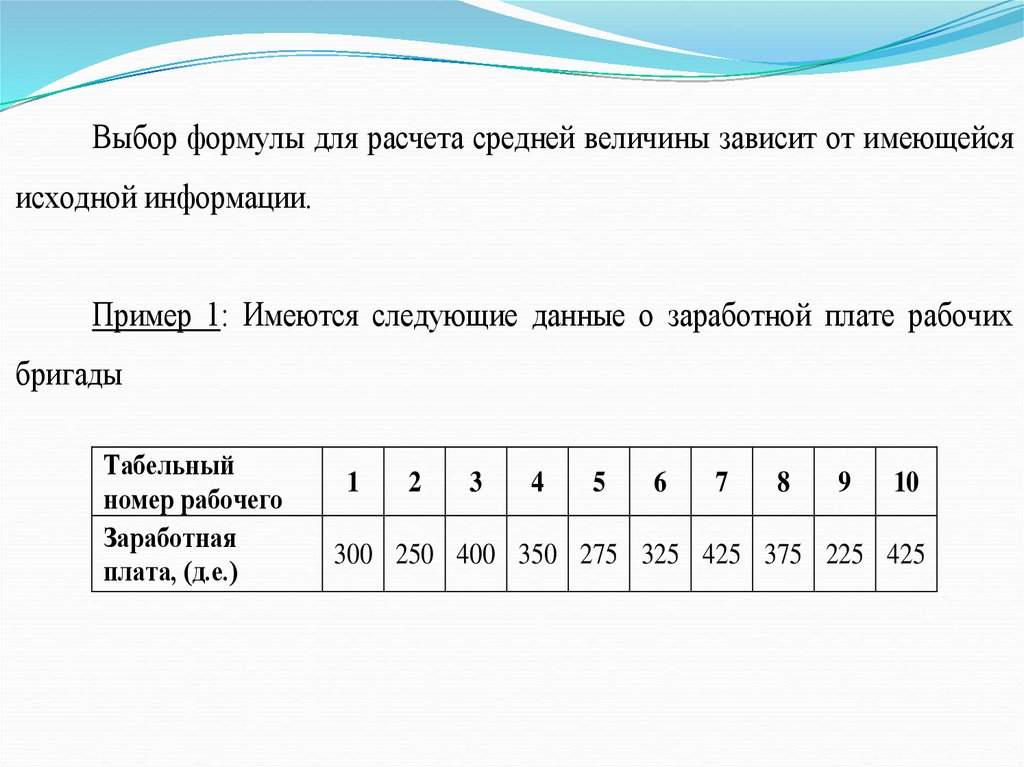
Выбор формулы для расчета средней величины зависит от имеющейсяисходной информации.
Пример 1: Имеются следующие данные о заработной плате рабочих
бригады
Табельный
номер рабочего
Заработная
плата, (д.е.)
1
2
3
4
5
6
7
8
9
10
300 250 400 350 275 325 425 375 225 425
102.
если каждое значение признака встречается один или одинаковое число раз,для расчета средней величины признака используется формула средней
арифметической простой.
Пример 2: Имеются следующие данные:
№
бригады
Число рабочих
1
2
10
12
Заработная плата
одного рабочего
(д.е.)
250
300
Определить среднюю заработную плату рабочего по 2 бригадам.
Исходя из имеющихся данных фонд заработной платы по каждой
бригаде определим путем умножения заработной платы одного рабочего (x) на
число рабочих(f ), а по двум бригадам вместе как сумму x f , тогда
103.
Если каждое значение признака встречается несколько раз, для расчетасредней
величины
взвешенной.
используется
формула
средней
арифметической
104.
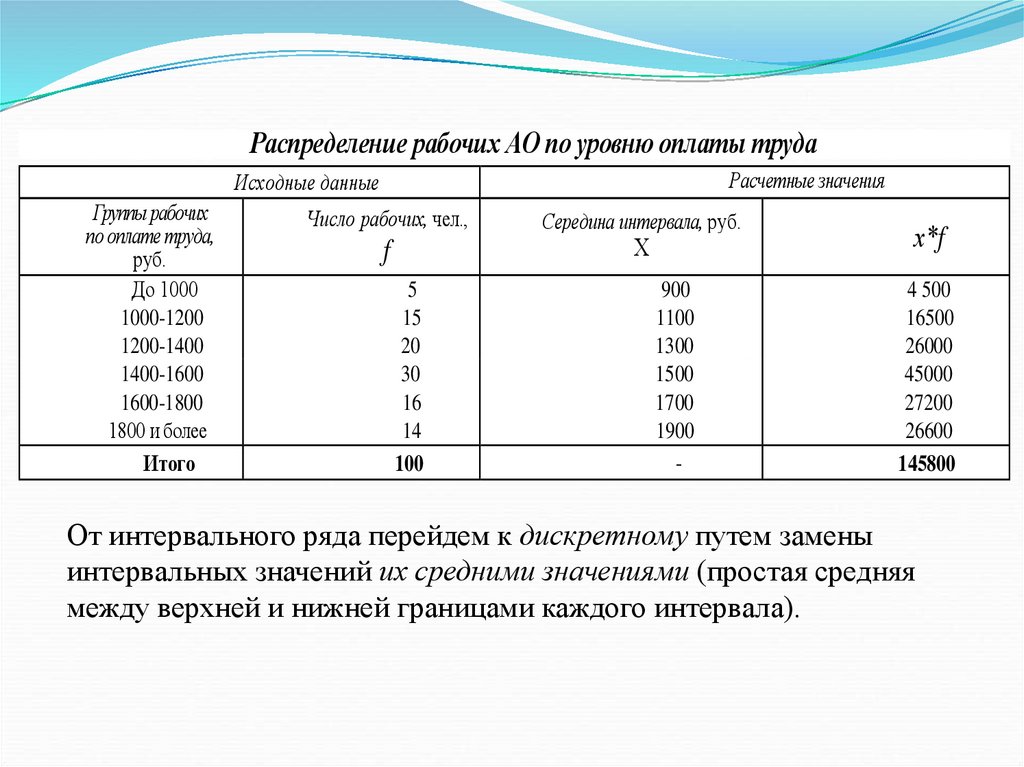
Расчет средней арифметической в рядах распределенияЕсли значения осредняемого признака заданы в виде интервалов ("от — до"), т.е. интервальных рядов распределения, то
при расчете средней арифметической величины в качестве
значений признаков в группах принимают середины этих
интервалов, в результате чего образуется дискретный ряд.
Рассмотрим следующий пример:
105.
Распределение рабочих АО по уровню оплаты трудаИсходные данные
Группы рабочих
по оплате труда,
руб.
До 1000
1000-1200
1200-1400
1400-1600
1600-1800
1800 и более
Итого
Число рабочих, чел.,
Расчетные значения
Шачения
Середина интервала, руб.
Х
f
5
15
20
30
16
14
100
900
1100
1300
1500
1700
1900
-
х*f
4 500
16500
26000
45000
27200
26600
145800
От интервального ряда перейдем к дискретному путем замены
интервальных значений их средними значениями (простая средняя
между верхней и нижней границами каждого интервала).
106.
При этом величины открытых интервалов (первый и последний) условноприравниваются к интервалам, примыкающим к ним (второй и
предпоследний).
При таком исчислении средней допускается некоторая неточность,
поскольку делается предположение о равномерности распределения
единиц признака внутри группы. Однако ошибка будет тем меньше, чем
уже интервал и чем больше единиц в интервале.
После того как найдены середины интервалов, вычисления делают так
же, как и в дискретном ряду, — варианты умножают на частоты (веса) и
сумму произведений делят на сумму частот (весов),
xf 145800
x
1458
100
f
ap
107.
Средняя гармоническая может быть простой и взвешенной.Простая средняя гармоническая рассчитывается по формуле:
= .
где
— индивидуальное значение признака (варианта);
n — объем совокупности (число единиц совокупности).
Средняя гармоническая взвешенная при меняется вместо
средней арифметической взвешенной, когда нет данных о частотах
отдельных вариант ( ) совокупности, но есть данные о величине
произведения –
.
Средняя гармоническая взвешенная рассчитывается по
формуле
= ,
где
108.
Пример.У
предпринимателя
имеются
два
автомобиля
различных моделей, работающих на бензине одинаковой
марки. Расход бензина у первого автомобиля равен 0,05 л/км, у
второго — 0,08 л/км. Каков средний расход бензина на 100 км
(или 1 км) пройденного пути?
Может показаться, что решение этой задачи заключается в
расчете средней арифметической простой, т.е. расход, л/км,
равен (0,05+0,008) : 2 = 0,065.
Однако такой расчет является ошибочным.
109.
измениться определяющий показатель — в данном случае общий пробег.Принимая x ap = 0,065 л/км, общий пробег, км, оказывается меньше на 69,23 км, так как 40 : 0,065 +
40 : 0,065 = 1230,77, что подтверждает ошибочность выполненного расчета простой средней.
Правильное решение этой задачи должно в своей основе содержать исходное (логическое)
соотношение средней.
Для того чтобы определить средний расход бензина на 1км
пройденного пути ( x гap , л/км), необходимо общий расход бензина поделить на суммарный пробег обоих
автомобилей:
хгар
40 40
0,0615 ,
40
40
0,05 0,08
или 6,15 л на 100 км.
Как видим, расчет сведен к исчислению средней гармонической простой (при этом конкретное
количество израсходованного бензина роли в расчете не играет, главное, чтобы оно было одинаковым).
При замене индивидуальных значений признака их средней ( x гap ) общий пробег не изменится:
40
40
1300 км.
0,0615 0,0615
110.
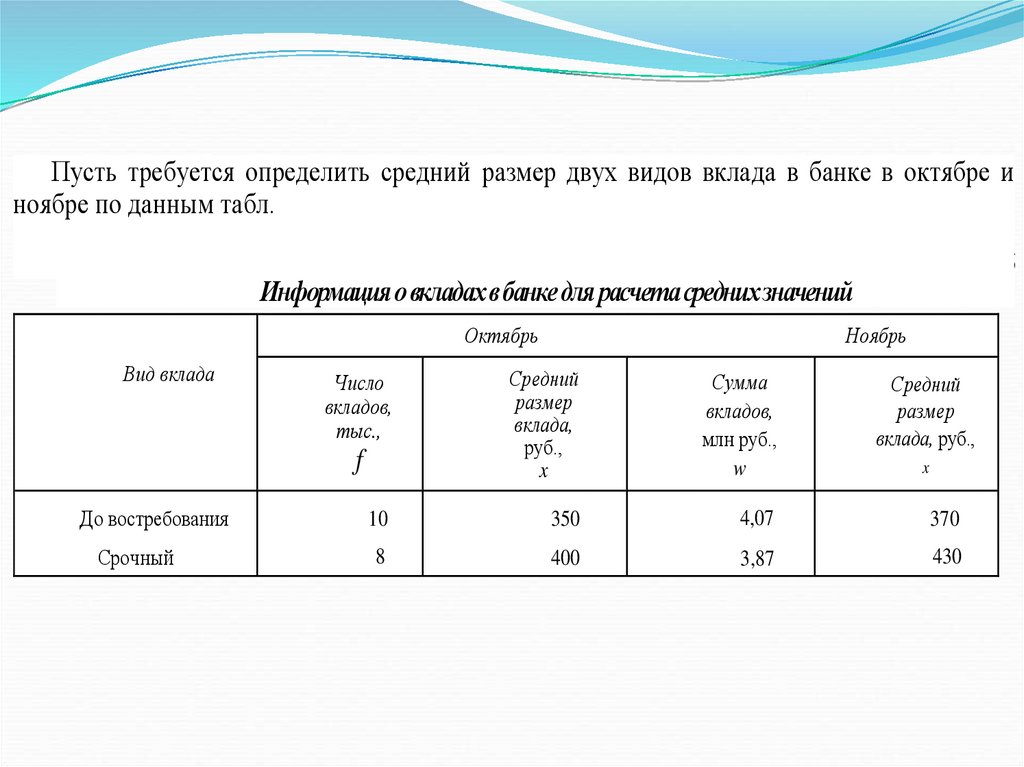
Пусть требуется определить средний размер двух видов вклада в банке в октябре иноябре по данным табл. 5.6.
Информация о вкладах в банке для расчета средних значений
Октябрь
Вид вклада
Срочный
Ноябрь
Средний
размер
вклада,
руб.,
x
Сумма
вкладов,
млн руб.,
w
10
350
4,07
370
8
400
3,87
430
Число
вкладов,
тыс.,
f
До востребования
Таблица 5.6
Средний
размер
вклада, руб.,
x
111.
Найти: Средний размер вклада по двумвидам:
- в октябре
- в ноябре
112.
В октябре известен средний размер вкладов каждого вида х и количество вкладов f.Следовательно, для расчета среднего размера вклада по двум видам применяем формулу
средней арифметической взвешенной, руб.:
xf 350 10000 400 8000 372,22 .
xap
10000 8000
f
В ноябре известен средний размер вкладов каждого вида, а количество вкладов — не
известно, но зато имеются данные об общих суммах этих вкладов.
Путем деления сумм вкладов w каждого вида на их средний размер вклада х можно определить
веса — число вкладов f по их видам, а затем определить средний размер вклада по двум видам
по формуле средней арифметической взвешенной.
113.
средний размер вклада в ноябре по двум их видам находим по формуле средней гармоническойвзвешенной, руб.:
xгар
w 4070000 3870000 7940000 397 .
w 4070000 3870000
20000
x
370
430
Общее правило: при расчете среднего уровня признака,
представляющего собой относительную величину, используются
средние взвешенные: арифметическая и гармоническая. Выбор вида
средней в каждом конкретном случае определяется имеющейся
информацией. Если имеется информация о знаменателе формулы, по
которой определяется усредняемый признак, то используется средняя
арифметическая. Если же имеется информация о числителе этой
формулы, то используется средняя гармоническая.
114.
Средняя геометрическая простая определяется по формуле.
Средняя геометрическая взвешенная определяется по
формуле
.
где — значения признака;
– частота, соответствующая .
115.
В экономической статистике средняя геометрическаяприменяется при определении средних коэффициентов и темпов
роста в рядах динамики.
Средняя квадратическая простая определяется по формуле
.
Средняя
формуле
квадратическая
взвешенная
определяется
по
Средняя квадратическая используется при оценке уровня
вариации анализируемых экономических показателей.












































































































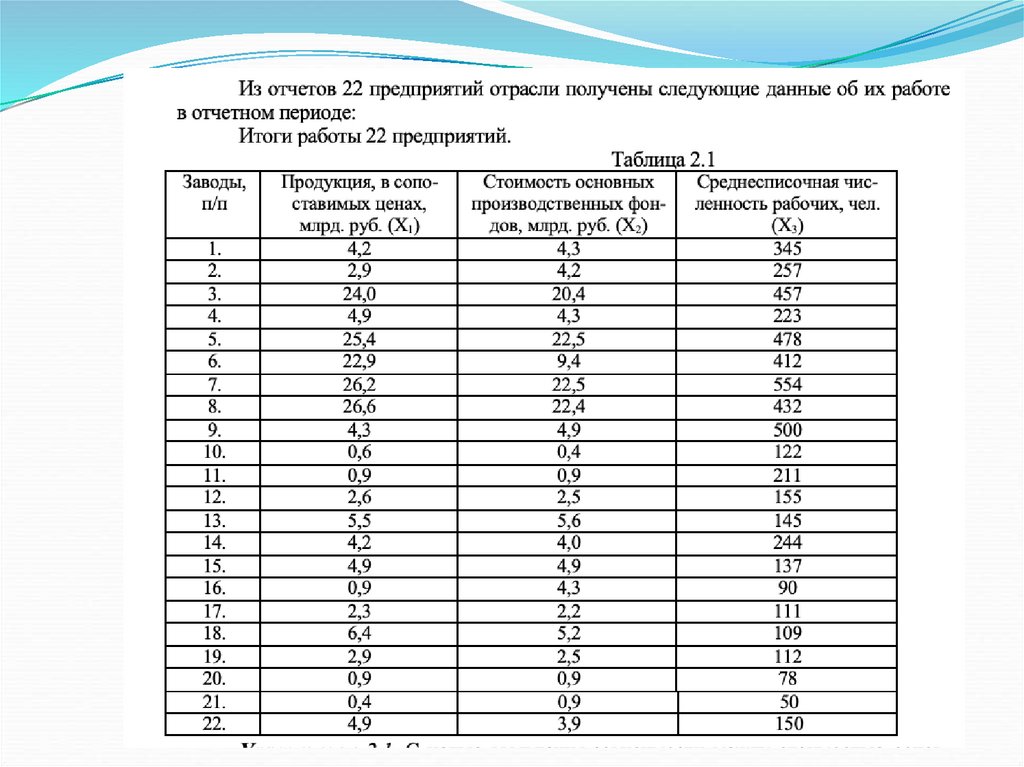

 Математика
Математика








