Исследовательская деятельность обучающихся по математике. Решения задач исследовательского характера

1.

Исследовательская
деятельность обучающихся
по математике
Обучение – это ремесло,
использующее
бесчисленное количество маленьких
трюков.
Д. Пойа

2.

Математика всегда была
неотъемлемой и существенной
составной частью человеческой
культуры, она является ключом к
познанию окружающего мира, базой
научно-технического прогресса и
важной компонентой развития
личности.

3.

Важно воспитать в человеке способность понимать
смысл поставленной перед ним задачи, умение
правильно, логично рассуждать, усвоить навыки
алгоритмического мышления. Каждому необходимо
научиться анализировать, отличать гипотезу от факта,
критиковать, схематизировать, отчетливо выражать
свои мысли, с другой стороны - развить воображение
и интуицию (пространственное представление,
способность предвидеть результат и предугадать путь
решения). Иначе говоря, математика нужна для
интеллектуального развития личности. Математика
дает широкое поле для исследования.

4.

В исследовательской деятельности главной целью является
получение объективно новых знаний. При этом оцениваются
не только знания, но и рассматриваются другие показатели,
такие как:
-участие в дискуссиях;
-умение высказывать свою точку зрения;
-сбор материала из различных источников;
-активность при обсуждении вопросов;
-умение задавать вопросы;
- возможность выразить свое отношение к изучаемому
материалу.

5.

При решении исследовательских задач у учащихся часто
возникают затруднения, поэтому учителю следует задавать
наталкивающие вопросы.
Уметь задавать вопросы – одно из важнейших умений
учителя, так как умело заданный вопрос обеспечивает
правильный и конкретный ответ учащихся.
По характеру ответов вопросы могут быть :
-репродуктивные (воспроизведение знаний; например,
перечислить компоненты процесса обучения);
-реконструктивные (требующие применения знаний в
нестандартной ситуации: например, чем отличаются …,
какова основная мысль…)
-;
- творческие (требующие осмысления и творческого подхода).

6.

Задания, исследовательского характера существенно отличаются от
традиционных заданий уже своей формулировкой. Так большая часть
заданий школьных учебников звучит так: «Решить уравнение», «Доказать,
что выражение … больше выражения …», «Упростите…» и т. п. В
формулировках исследовательских заданий нет явного ответа, его
необходимо самим найти и обосновать. Формулировки заданий могут быть
такими:
1. «Исследовать …».
2. «Верно ли, что если …, то …».
3.Определить, какое из выражений больше ».
4. «Найти необходимое и достаточное условие, при котором обе
последовательности стремятся к нулю».
5. «Существуют ли такие значения b, при которых квадратный трехчлен
имеет два корня, один из которых является положительным числом, а
другой отрицательным?».
6. «Существуют ли такие значения с, что множеством решений
неравенства … является: а) числовой промежуток …; б) множество всех
чисел».
7. «Верно ли, что функция … при любом а убывает в промежутке … и
возрастает в промежутке …?».

7.

После решения задач исследовательского
характера необходимо, чтобы учащиеся
осуществляли исследование ответа, вывода
(т. е. ставили вопрос о существовании
решения, о числе решений,
об особых случаях, какие могут
представиться) при рассмотрении каждой
задачи,
особенно такой, которая предлагается в
общем виде.

8.

Я использую
разнообразные формы работы
как коллективный поиск,
работа в паре,
группе,
так и индивидуальная форма работы

9.

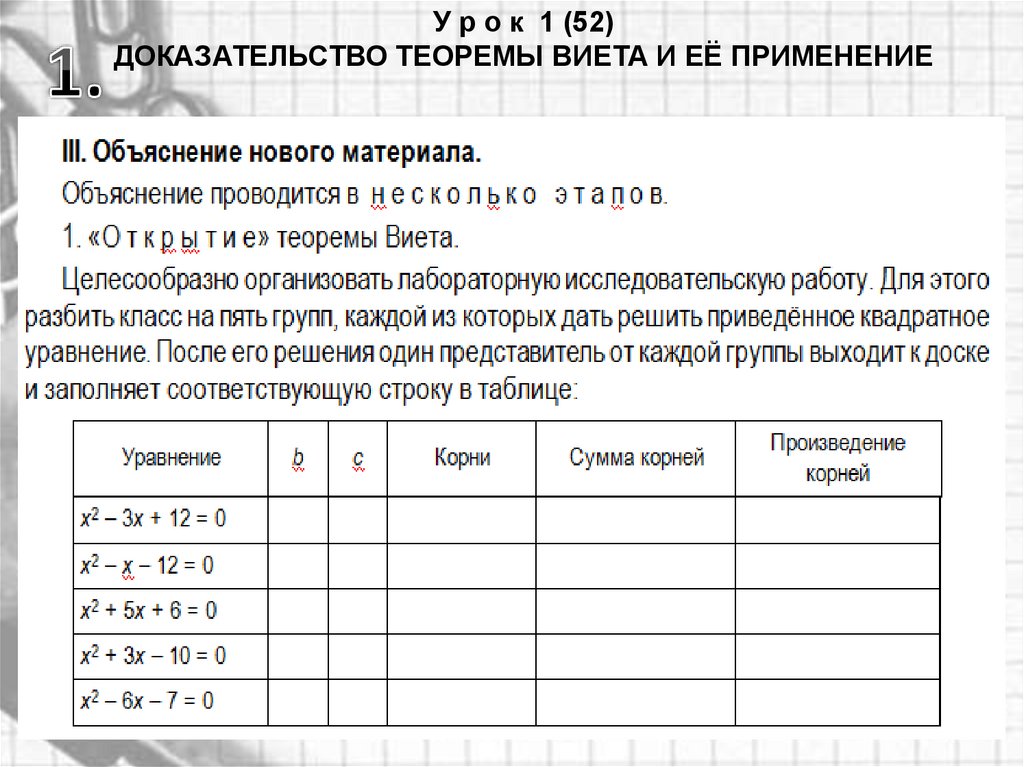
У р о к 1 (52)
ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ ВИЕТА И ЕЁ ПРИМЕНЕНИЕ

10.

11.

Задачи со старинными мерами длины:
1. Каков рост в миллиметрах у Дюймовочки в одноимённой сказке
Г-Х. Андерсена?
2. А.С. Пушкин говорит, что у царя Салтана родился сын «в
аршин». Найдите рост будущего князя Гвидона в сантиметрах.
3. Обычное пожелание морякам перед плаванием: «Семь футов
под килем!». Сколько это будет в сантиметрах?
4. Кольцо баскетбольной корзины расположено на высоте 10
футов. Найдите эту высоту в метрах, сантиметрах и миллиметрах.
5. Длина футбольных ворот 7 м 32 см, а высота 2 м 44 см. Найдите
размеры ворот в футах (можно считать фут = 30 см 5 мм).
6. В хоккей на траве играют на прямоугольной площадке со
сторонами 91 м 50 см и 54 м 90 см. Найдите длины сторон в
ярдах.
7. Выразите в дюймах и сантиметрах 1 вершок, 1 пядь, 1 аршин, 1
сажень.
8. Верста – 500 саженей. Найдите длину версты в метрах.
9. Есть поговорка «пять вёрст до небес, и всё лесом». Сколько
метров «до небес»?

12.

Расположите старинные меры длины по возрастанию

13.

14.

"Нужно ли Вам уметь извлекать квадратные
корни многозначных чисел без
калькулятора?"
«да»
8%
«затрудняюсь
ответить»
92%

15.

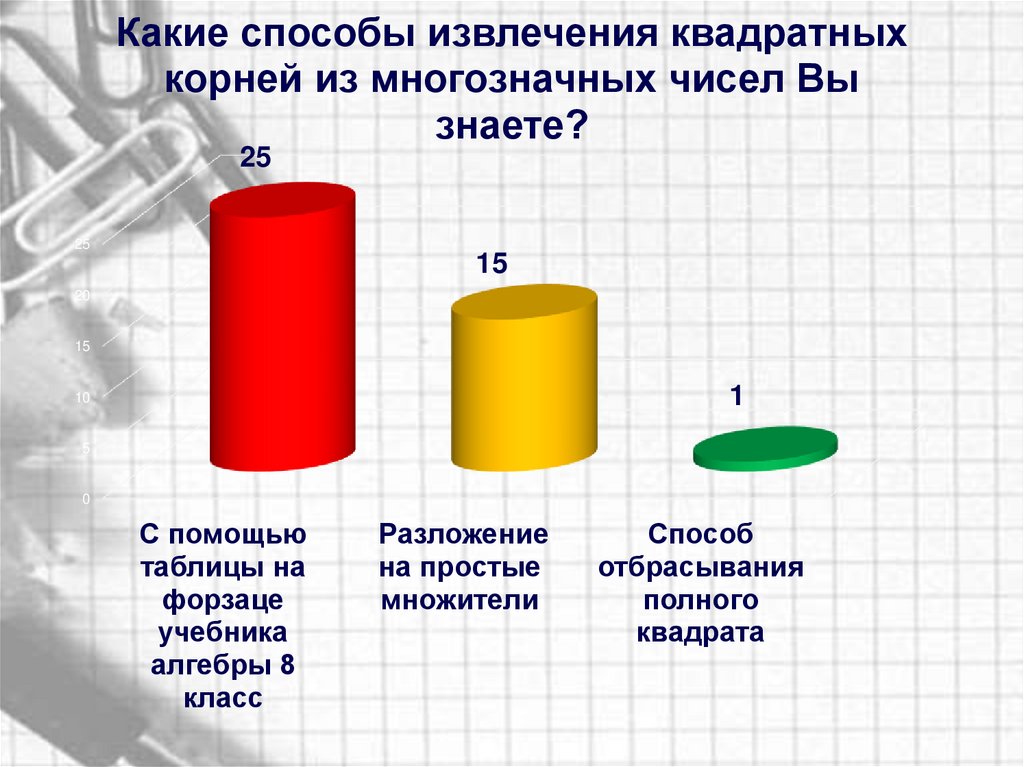
Какие способы извлечения квадратных
корней из многозначных чисел Вы
знаете?
25
25
15
20
15
1
10
5
0
С помощью
таблицы на
форзаце
учебника
алгебры 8
класс
Разложение
на простые
множители
Способ
отбрасывания
полного
квадрата

16.

Вывод:
Результаты показали, что ученики хорошо
умеют пользоваться таблицей квадратов
двузначных чисел, но не умеют извлекать корни
из многозначных чисел больших 1002.

17.

Гипотеза:
Существует не менее двух-трёх
способов
извлечения квадратных корней без
калькулятора.

18.

Цель работы:
изучить способы вычисления арифметических
корней и выбрать самый рациональный для
практического применения.

19.

Задачи проекта:
1. Проанализировать путём соцопроса умение
учащихся извлекать квадратные корни без калькулятора;
2.Изучить математическую литературу по данной теме,
используя Интернет-ресурсы;
3. Изучить способы и алгоритмы вычисления арифметического
корня и рассмотреть примеры быстрого извлечения квадратного
корня;
3. Классифицировать найденные способы извлечения корней
по степени сложности, погрешности и практическому
применению;
4. Познакомить одноклассников с самым
рациональным способом извлечения корней
и выпустить буклет-памятку по данному способу.

20.

Актуальность
В школьном курсе математики часто встречаются
задания с извлечением квадратного корня, в
заданиях ОГЭ, в практических вычислениях и быту.
Умения извлекать квадратные корни нужны при
изучении некоторых тем химии и физики .

21.

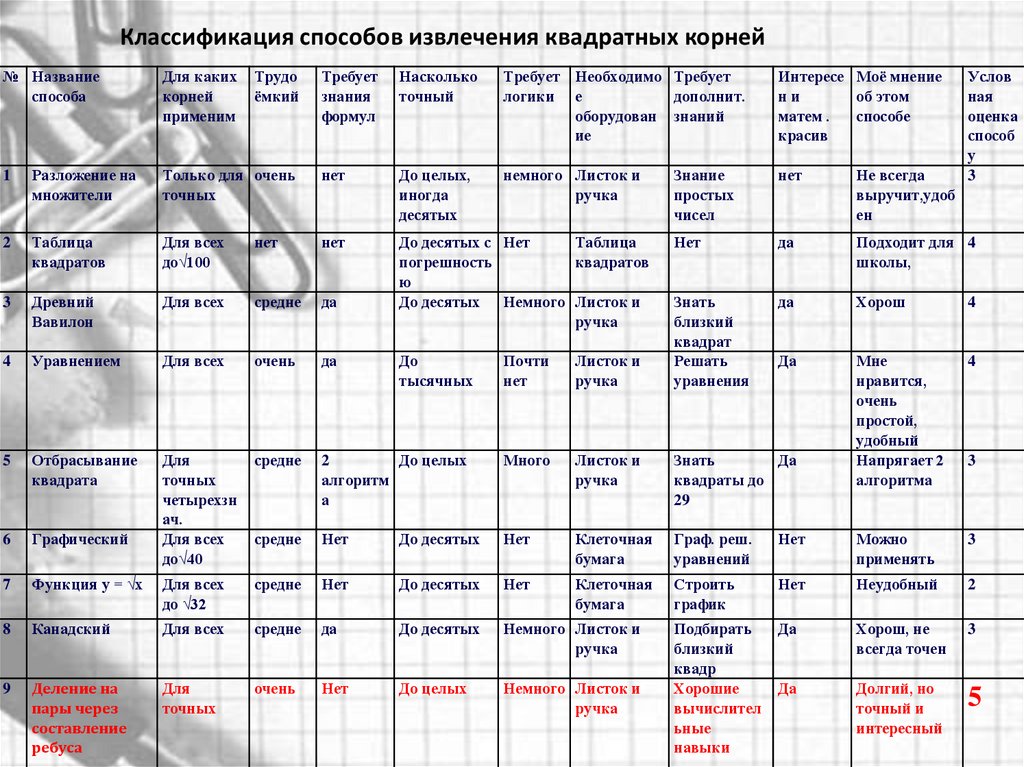
Классификация способов извлечения квадратных корней
№ Название
способа
Для каких
корней
применим
Трудо
ёмкий
Требует
знания
формул
Насколько
точный
Требует Необходимо Требует
логики е
дополнит.
оборудован знаний
ие
Интересе Моё мнение
ни
об этом
матем .
способе
красив
немного Листок и
ручка
Знание
простых
чисел
нет
Не всегда
выручит,удоб
ен
Нет
да
Подходит для 4
школы,
Знать
близкий
квадрат
Решать
уравнения
да
Хорош
4
Да
Мне
нравится,
очень
простой,
удобный
Напрягает 2
алгоритма
4
1
Разложение на
множители
Только для очень
точных
нет
До целых,
иногда
десятых
2
Таблица
квадратов
Для всех
до√100
нет
нет
3
Древний
Вавилон
Для всех
средне
да
До десятых с Нет
Таблица
погрешность
квадратов
ю
До десятых Немного Листок и
ручка
4
Уравнением
Для всех
очень
да
5
Отбрасывание
квадрата
средне
6
Графический
Для
точных
четырехзн
ач.
Для всех
до√40
7
Функция у = √х
8
9
До
тысячных
Услов
ная
оценка
способ
у
3
Почти
нет
Листок и
ручка
2
До целых
алгоритм
а
Много
Листок и
ручка
Знать
Да
квадраты до
29
средне
Нет
До десятых
Нет
Клеточная
бумага
Граф. реш.
уравнений
Нет
Можно
применять
3
Для всех
до √32
средне
Нет
До десятых
Нет
Клеточная
бумага
Строить
график
Нет
Неудобный
2
Канадский
Для всех
средне
да
До десятых
Немного Листок и
ручка
Да
Хорош, не
всегда точен
3
Деление на
пары через
составление
ребуса
Для
точных
очень
Нет
До целых
Немного Листок и
ручка
Подбирать
близкий
квадр
Хорошие
вычислител
ьные
навыки
Да
Долгий, но
точный и
интересный
5
3

22.

Заключение
В ходе нашего исследования, мы убедились, что актуальность темы мы
выбрали правильную, ведь не только дети, но и взрослые не умеют
вычислять квадратные корни без калькулятора, а это является важной
составляющей в жизни людей.
Методом проб и ошибок, мы пришли к выводу, что самым
рациональными точным является способ «Деление на пары через
составление ребуса»
В результате нашей исследовательской работы мы познакомили своих
одноклассников с самым рациональным, по нашему мнению, методом
«Деление на пары через составление ребуса» из-за удобства, точности,
доступности, вручили памятку-буклет данного метода. Так пришли к
выводу, что извлечение квадратного корня без калькулятора является не
только полезным занятием, но еще и очень увлекательным.

23.

24.

25.

26.

Спасибо
за внимание);