Похожие презентации:
Тела вращения. Цилиндр. Конус. Шар. Сфера
1.
Тема: Тела вращения. Цилиндр. Конус. Шар.Сфера
2.
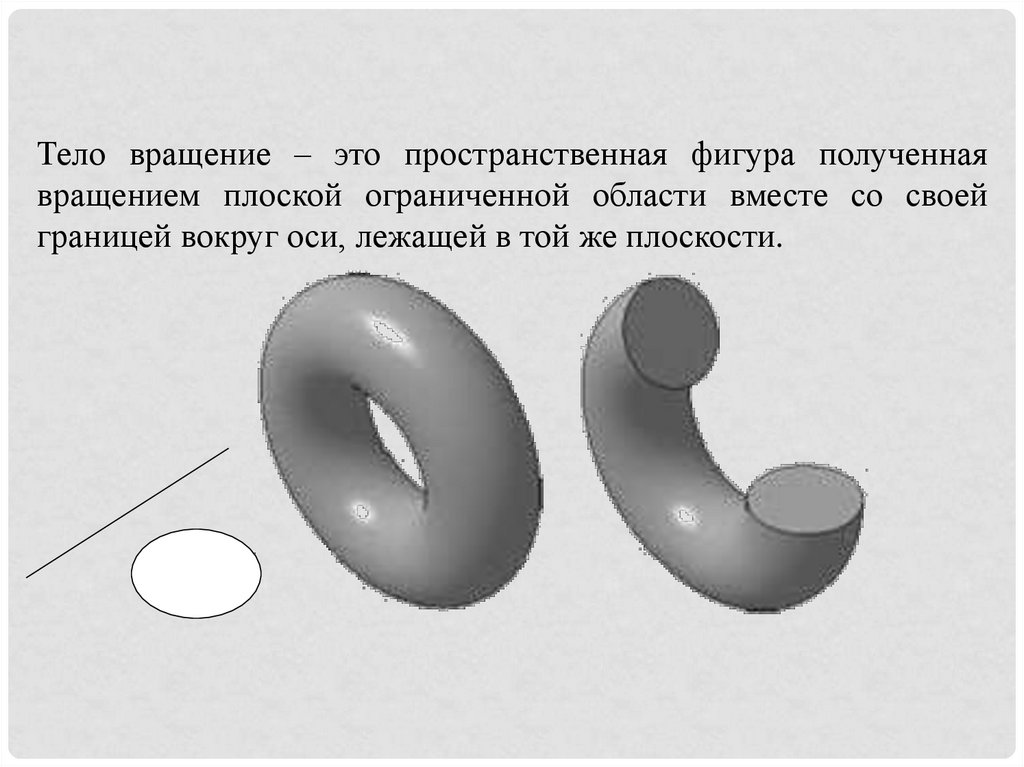
Тело вращение – это пространственная фигура полученнаявращением плоской ограниченной области вместе со своей
границей вокруг оси, лежащей в той же плоскости.
3.
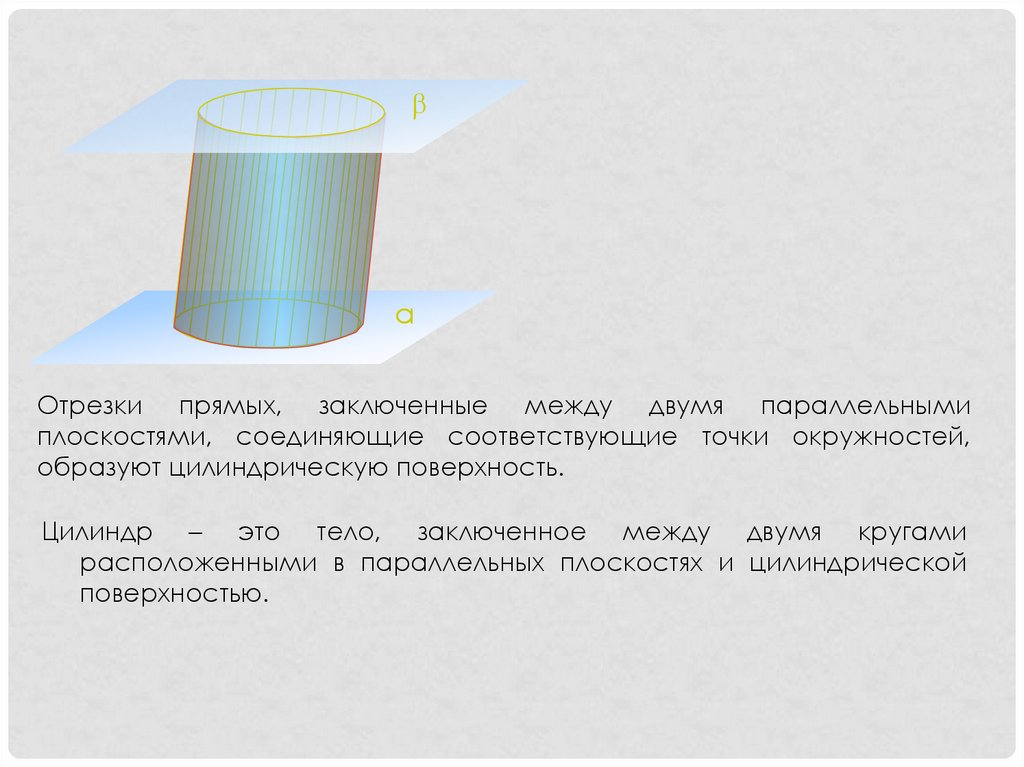
αОтрезки прямых, заключенные между двумя параллельными
плоскостями, соединяющие соответствующие точки окружностей,
образуют цилиндрическую поверхность.
Цилиндр – это тело, заключенное между двумя кругами
расположенными в параллельных плоскостях и цилиндрической
поверхностью.
4.
основаниеось
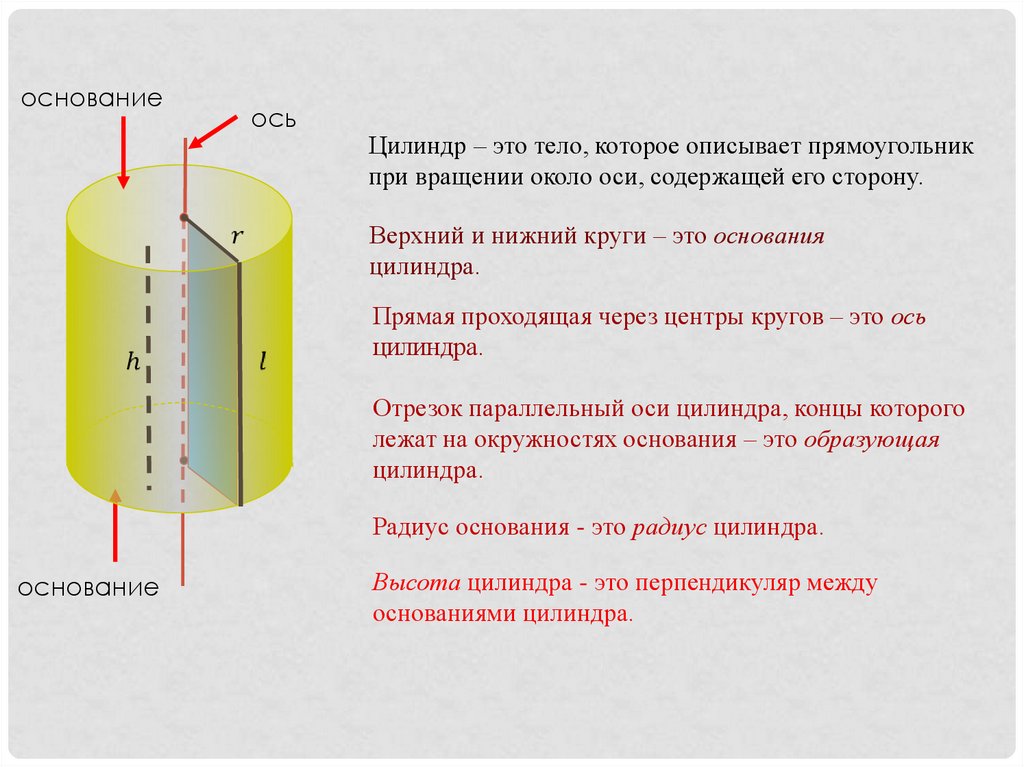
Цилиндр – это тело, которое описывает прямоугольник
при вращении около оси, содержащей его сторону.
Верхний и нижний круги – это основания
цилиндра.
Прямая проходящая через центры кругов – это ось
цилиндра.
Отрезок параллельный оси цилиндра, концы которого
лежат на окружностях основания – это образующая
цилиндра.
Радиус основания - это радиус цилиндра.
основание
Высота цилиндра - это перпендикуляр между
основаниями цилиндра.
5.
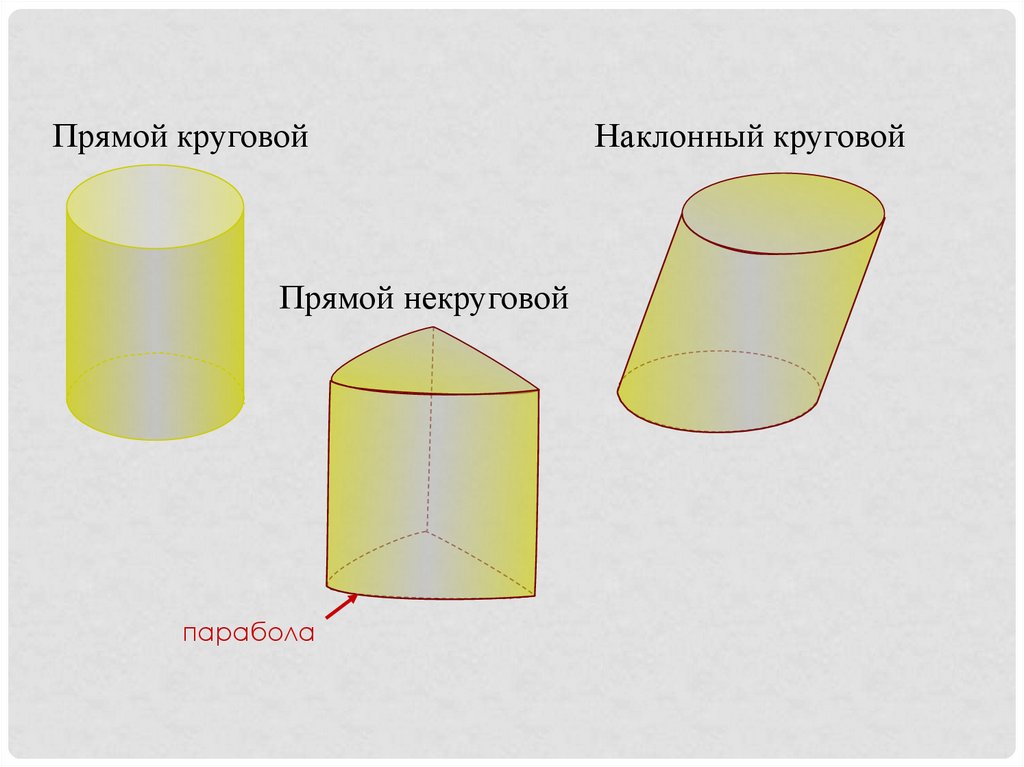
Прямой круговойПрямой некруговой
парабола
Наклонный круговой
6.
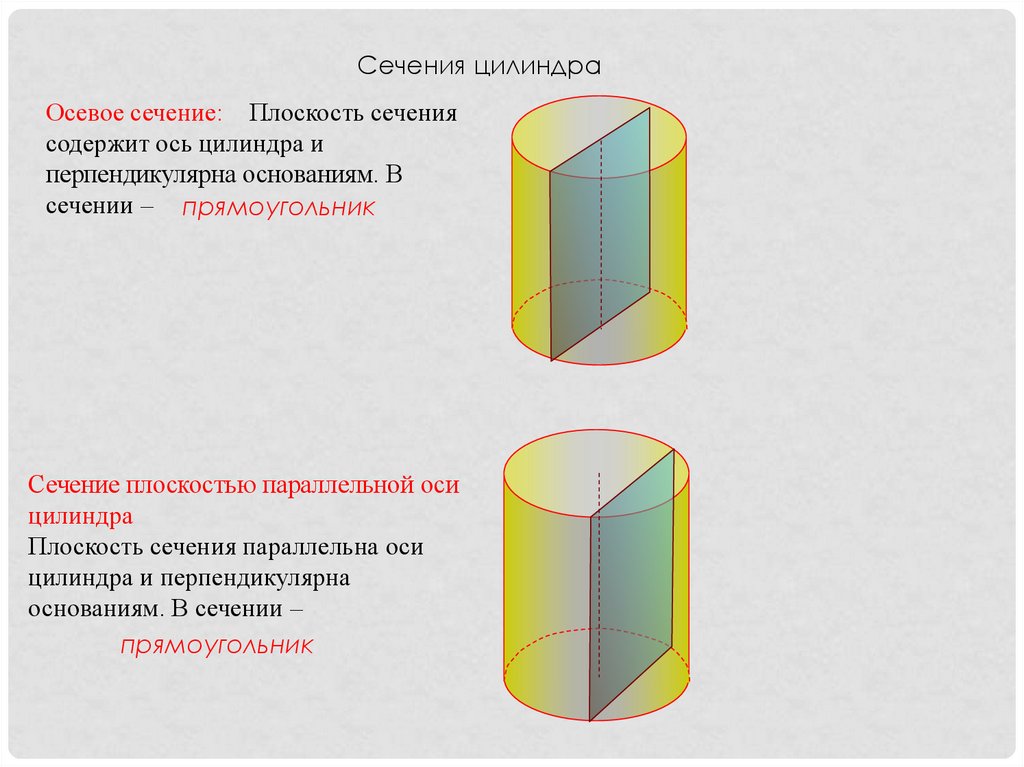
Сечения цилиндраОсевое сечение: Плоскость сечения
содержит ось цилиндра и
перпендикулярна основаниям. В
сечении – прямоугольник
Сечение плоскостью параллельной оси
цилиндра
Плоскость сечения параллельна оси
цилиндра и перпендикулярна
основаниям. В сечении –
прямоугольник
7.
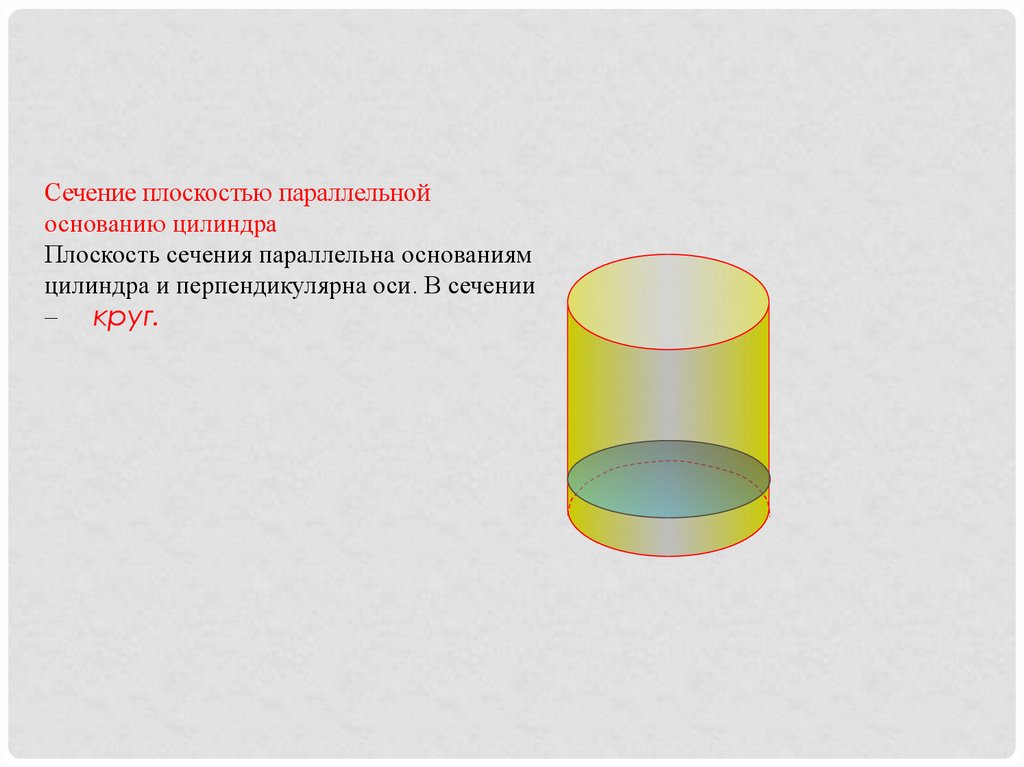
Сечение плоскостью параллельнойоснованию цилиндра
Плоскость сечения параллельна основаниям
цилиндра и перпендикулярна оси. В сечении
– круг.
8.
Площадь поверхности цилиндраПлощадь основания находим
как площадь круга
S = r2
r – радиус основания цилиндра
h
Боковая поверхность цилиндра –
прямоугольник
2 r
r
r
Получаем, Sполн = Sбок + 2Sосн = 2 rh + 2 r2
Длина окружности
9.
КонусПоверхность, образованная отрезками с концами
на окружности и в точке С образуют
коническую поверхность.
С
Конус – это тело, ограниченное
конической поверхностью и
кругом, включая окружность.
α
10.
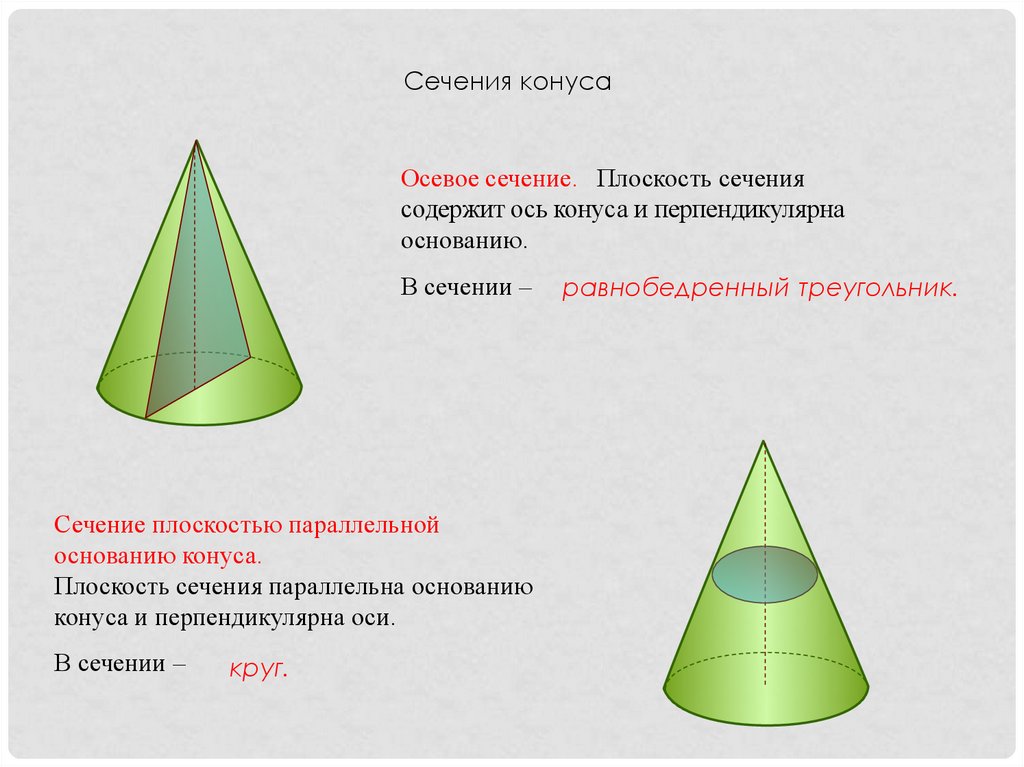
Сечения конусаОсевое сечение. Плоскость сечения
содержит ось конуса и перпендикулярна
основанию.
В сечении –
Сечение плоскостью параллельной
основанию конуса.
Плоскость сечения параллельна основанию
конуса и перпендикулярна оси.
В сечении –
круг.
равнобедренный треугольник.
11.
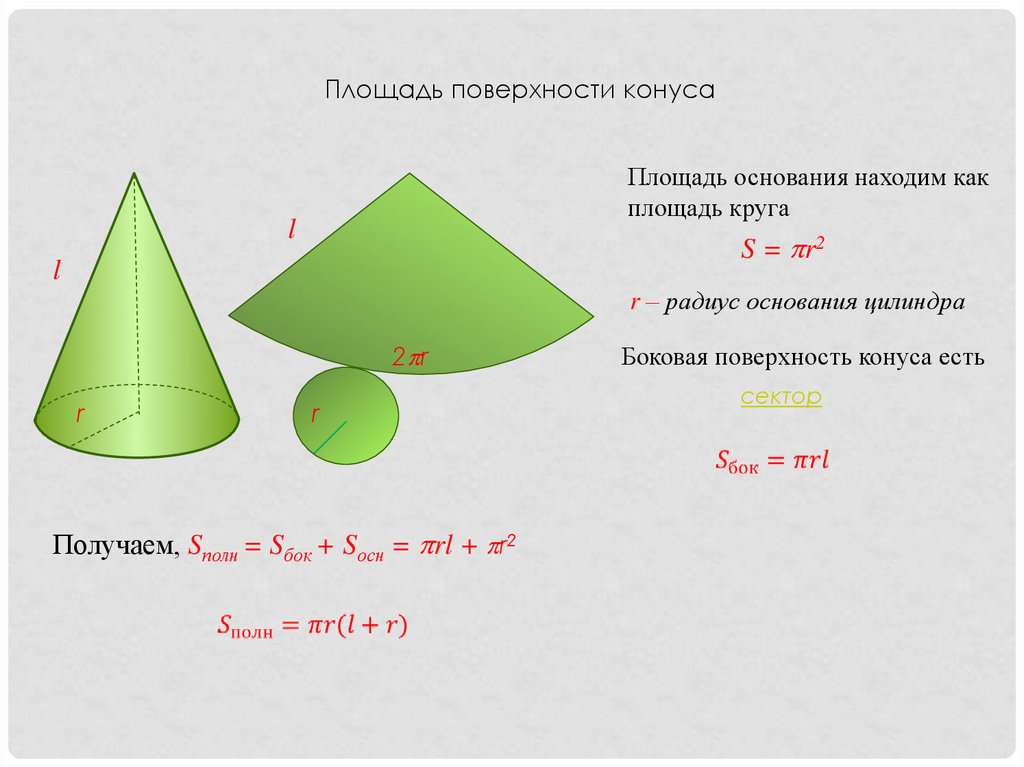
Площадь поверхности конусаПлощадь основания находим как
площадь круга
l
S = r2
l
r – радиус основания цилиндра
2 r
r
r
Получаем, Sполн = Sбок + Sосн = rl + r2
Боковая поверхность конуса есть
сектор
12.
Сфера. ШарСферой
называется
поверхность,
состоящая из всех точек пространства,
расположенных на данной расстоянии
от данной точки.
Эта точка будет являться центром сферы,
а расстояние радиусом сферы (R).
Отрезок, соединяющий две точки сферы
и проходящий через ее центр,
называется диаметром сферы.
Тело, ограниченное сферой, называется шаром.
Шар можно получить вращением полукруга вокруг оси, содержащей его диаметр
13.
Сечения шараСечение шара, проходящее через его центр.
В сечении – круг.
В этом случае в сечении получается круг
наибольшего радиуса, его называют
большой круг шара.
Сечение плоскостью, не проходящей через
центр.
В сечении – круг.
Теорема: Площадь поверхности шара равна четыре площади большого круга
шара.
14.
Взаимное расположение сферы и плоскостиd – расстояние от центра сферы до плоскости, R – радиус сферы
z
r – радиус сечения сферы
R
d
y
r
x
Вычислить радиус сечения
можно используя теорему
Пифагора.
r R d
2
2
d<R
Плоскость пересекает сферу и называется секущей
15.
Взаимное расположение сферы и плоскостиd – расстояние от центра сферы до плоскости, R – радиус сферы
z
Теорема: Радиус сферы проведенный в
точку касания сферы и плоскости,
перпендикулярен к касательной
плоскости.
R
y
x
R d 0
2
d=R
Плоскость имеет одну общую точку со
сферой и называется касательной
2
16.
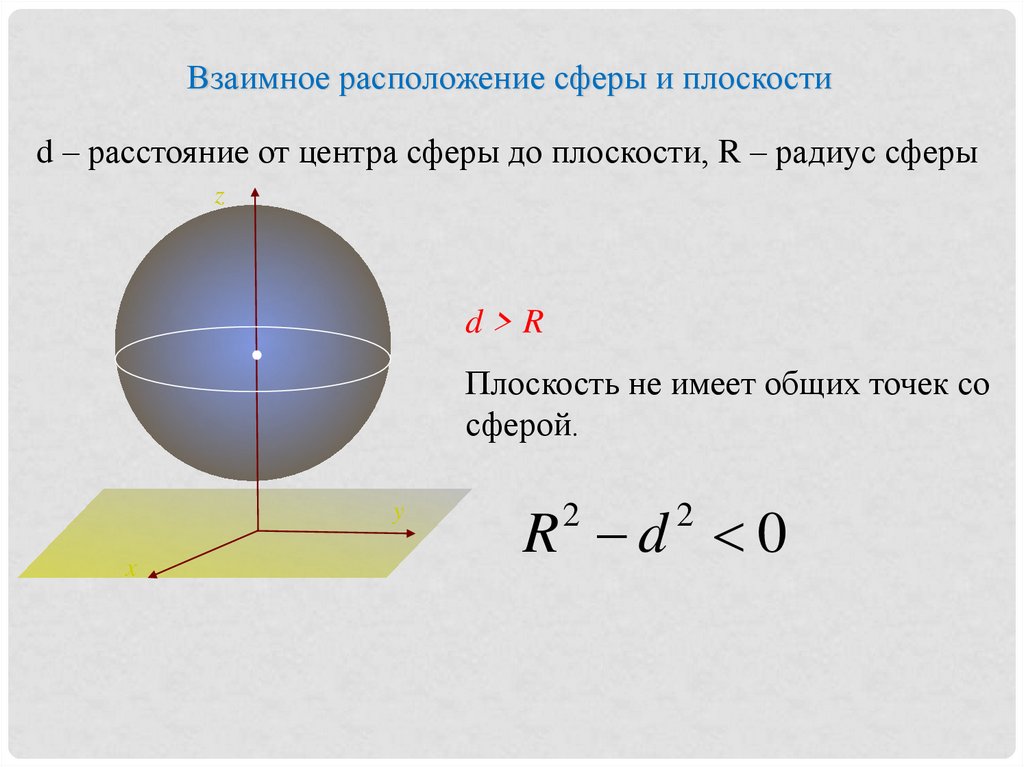
Взаимное расположение сферы и плоскостиd – расстояние от центра сферы до плоскости, R – радиус сферы
z
d>R
Плоскость не имеет общих точек со
сферой.
y
x
R d 0
2
2







 Математика
Математика








