Численные методы. Решение уравнений

1. Численные методы

Решение уравнений
© Д.А. Хрипунов 2009

2.

Решение уравнений
1. Основные понятия
2. Метод дихотомии
3. Метод итераций
4. Метод Ньютона (метод касательных)

3.

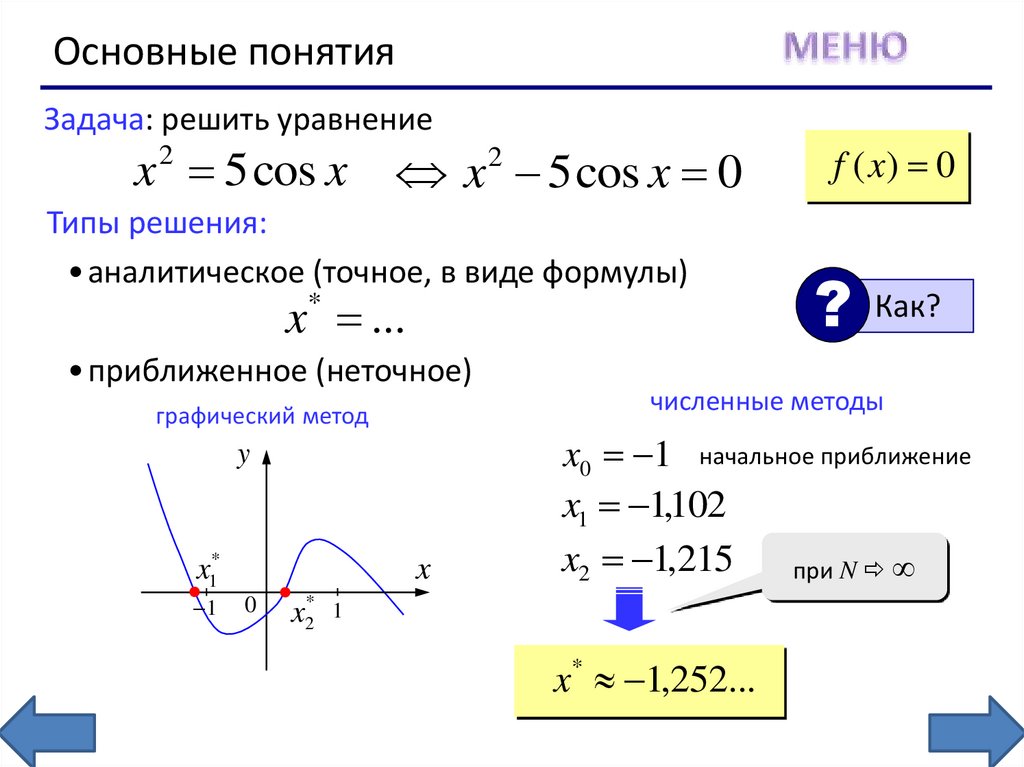
Основные понятия
Задача: решить уравнение
x 2 5 cos x
x 5 cos x 0
2
Типы решения:
•аналитическое (точное, в виде формулы)
x ...
*
•приближенное (неточное)
графический метод
y
x1*
1
x
0
f ( x) 0
? Как?
численные методы
x0 1 начальное приближение
x1 1,102
x2 1,215
при N
x2* 1
x* 1,252...
3

4.

Есть ли решение на [a, b]?
y
есть решение
y
нет решения
x*
a
y
нет решения
x*
bx
f (a) 0
f (b) 0
a b
a b
x
f (a) 0
f (b) 0
f (a) f (b) 0
x*
x
f (a) 0
f (b) 0
f (a ) f (b) 0
непрерывная функция f (x) имеет разные знаки
! Если
на концах интервалы [a, b], то в некоторой точке
внутри [a, b] имеем f (x) = 0!
4

5.

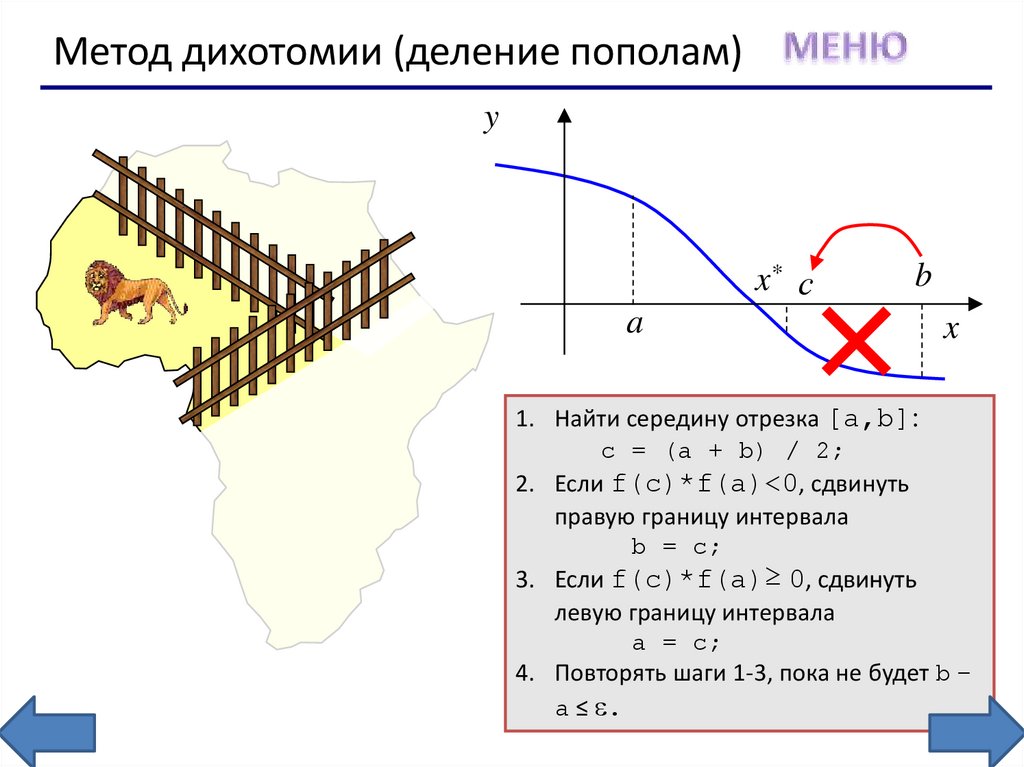
Метод дихотомии (деление пополам)
y
x* с
a
b
x
1. Найти середину отрезка [a,b]:
c = (a + b) / 2;
2. Если f(c)*f(a)<0, сдвинуть
правую границу интервала
b = c;
3. Если f(c)*f(a)≥ 0, сдвинуть
левую границу интервала
a = c;
4. Повторять шаги 1-3, пока не будет b –
a ≤ .
5

6.

Метод дихотомии (деления пополам)
•простота
•можно получить решение с заданной точностью (в
пределах точности машинных вычислений)
•нужно знать интервал [a, b]
•на интервале [a, b] должно быть только одно решение
•большое число шагов для достижения высокой
точности
•только для функций одной переменной
6

7.

Метод итераций (повторений)
Задача:
f ( x) 0
x ?
Эквивалентные преобразования:
b f ( x) 0 имеет те же решения при b 0
x b f ( x) x
x ( x),
( x) x b f ( x)
Идея решения:
x0 – начальное приближение (например, с графика)
xk ( xk 1 ) xk 1 b f ( xk 1 ), k 1, 2, ...
Проблемы:
1) как лучше выбрать? b
2) всегда ли так можно найти решение?
7

8.

Сходимость итераций
Сходящийся итерационный процесс: последовательность
приближается (сходится) к точному решению.
x0 , x1 , ...
x0 , x1 , x2 , ... x*
x ( x )
*
y
*
y x
y (x )
y
y (x )
( x0 )
( x0 )
x*
x0
x1 ( x0 )
односторонняя сходимость
x
x0
y x
x* x1 ( x0 ) x
двусторонняя сходимость
8

9.

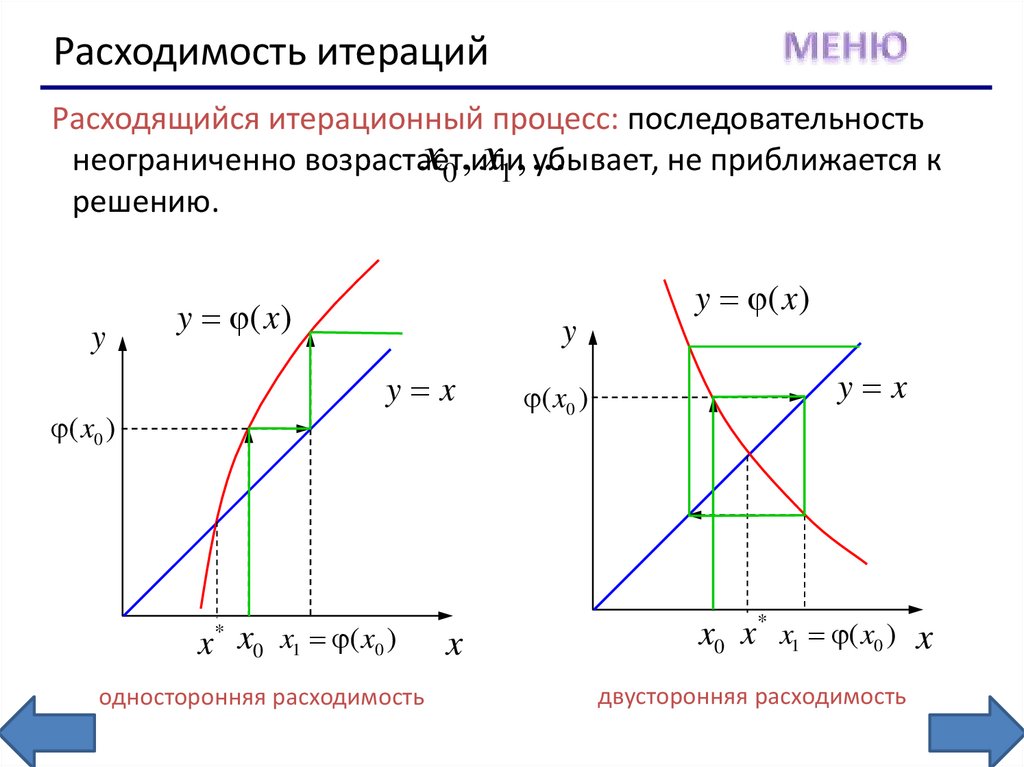
Расходимость итераций
Расходящийся итерационный процесс: последовательность
x0 ,или
x1 , ...
неограниченно возрастает
убывает, не приближается к
решению.
y
y (x )
y (x )
y
y x
( x0 )
x x0 x1 ( x0 )
*
односторонняя расходимость
x
( x0 )
y x
x0 x* x1 ( x0 ) x
двусторонняя расходимость
9

10.

От чего зависит сходимость?
сходится
y
0 ' ( x) 1
расходится
y (x )
y (x )
y
' ( x ) 1
y x
y x
x
y
y x
1 ' ( x) 0
y x
y
y (x )
' ( x) 1
y (x )
x
Выводы:
• сходимость итераций зависит от производной
x
x
' ( x)
при
' ( x) и расходятся
1
• сходимость определяется выбором параметра b
• итерации сходятся при
' ( x) 1
( x) x b f ( x) ' ( x) 1 b f ' ( x)
10

11.

Как выбрать b?
•наугад, пробовать разные варианты
•для начального приближения x0
1 1 b f ' ( x0 ) 1
f ' ( x0 ) 0
f ' ( x0 ) 0
2 b f ' ( x0 ) 0
2
b 0
f ' ( x0 )
2
0 b
f ' ( x0 )
•пересчитывать на каждом шаге, например:
1
1 b f ' ( xk ) 0 b
f ' ( xk )
? Какие могут быть проблемы?
11

12.

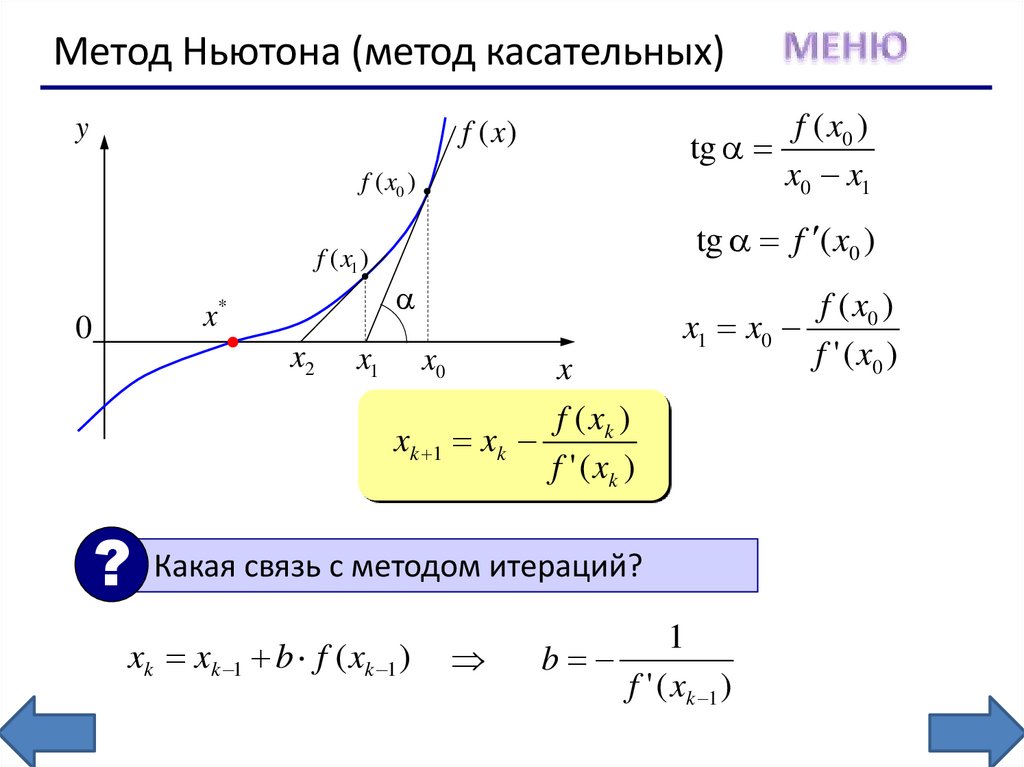
Метод Ньютона (метод касательных)
y
f ( x0 )
tg
x0 x1
f (x )
f ( x0 )
f ( x1 )
0
x*
x2
tg f ( x0 )
x1
x0
x
f ( x0 )
x1 x0
f ' ( x0 )
f ( xk )
xk 1 xk
f ' ( xk )
? Какая связь с методом итераций?
xk xk 1 b f ( xk 1 )
1
b
f ' ( xk 1 )
12

13.

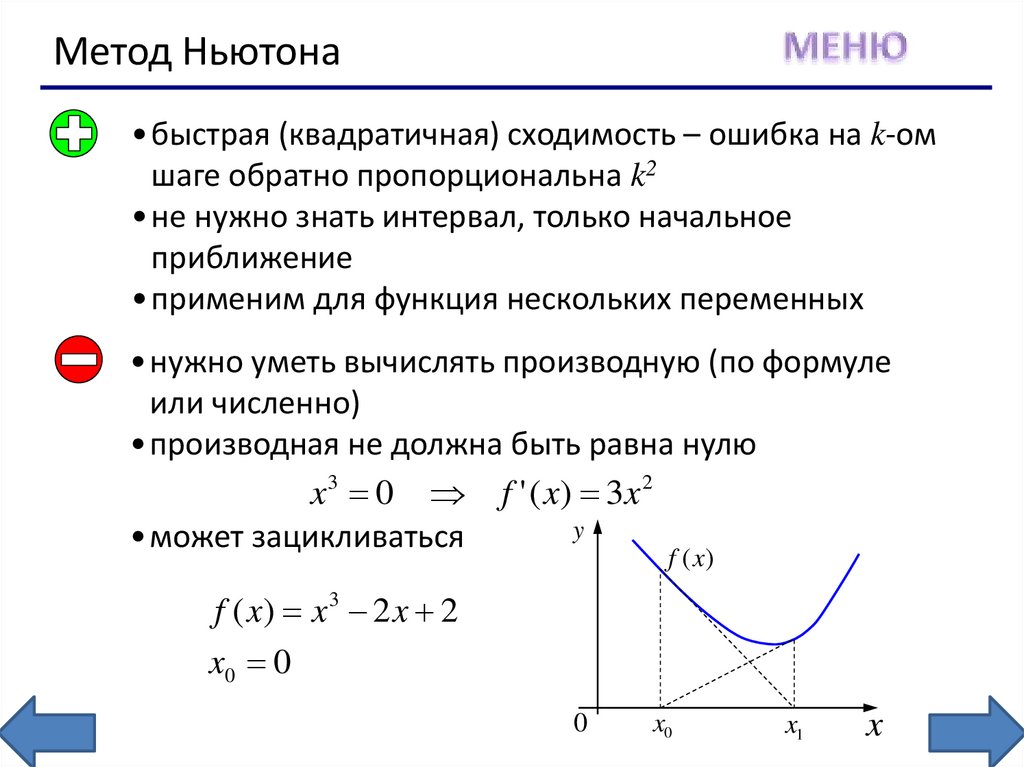
Метод Ньютона
•быстрая (квадратичная) сходимость – ошибка на k-ом
шаге обратно пропорциональна k2
•не нужно знать интервал, только начальное
приближение
•применим для функция нескольких переменных
•нужно уметь вычислять производную (по формуле
или численно)
•производная не должна быть равна нулю
x 3 0 f ' ( x) 3 x 2
y
•может зацикливаться
f (x )
f ( x) x 3 2 x 2
x0 0
0
x0
x1
x
13