Спектральный анализ сигналов. Лекция 1

1.

Спектральный анализ
сигналов
ЛЕКЦИЯ 1

2.

Спектральный (Фурье) и вейвлет-анализ – математическая основа цифровой
обработки сигналов (ЦОС или DSP - digital signal processing).
ЦОС является одной из новейших и самых мощных технологий, которая активно
внедрилась в широкий круг областей науки и техники: коммуникации, метеорология,
радиолокация и гидролокация, медицинская визуализация изображений, цифровое
аудио - и телевизионное вещание, разведка нефтяных и газовых месторождений, и
многих других. Можно сказать, что происходит повсеместное и глубокое
проникновение технологий цифровой обработки сигналов во все сферы деятельности
человечества.
Сегодня технология ЦОС относится к числу базовых знаний, которые необходимы
ученым и инженерам всех отраслей без исключения.

3.

Цифровая Обработка Сигналов выделяется из других областей знаний
вычислительной техники уникальным типом данных, который она использует –
сигналы.
В большинстве случаев эти сигналы представляют собой информацию от датчиков из
окружающего мира: сейсмические колебания, визуальные изображения, звуковые
волны и т.п.
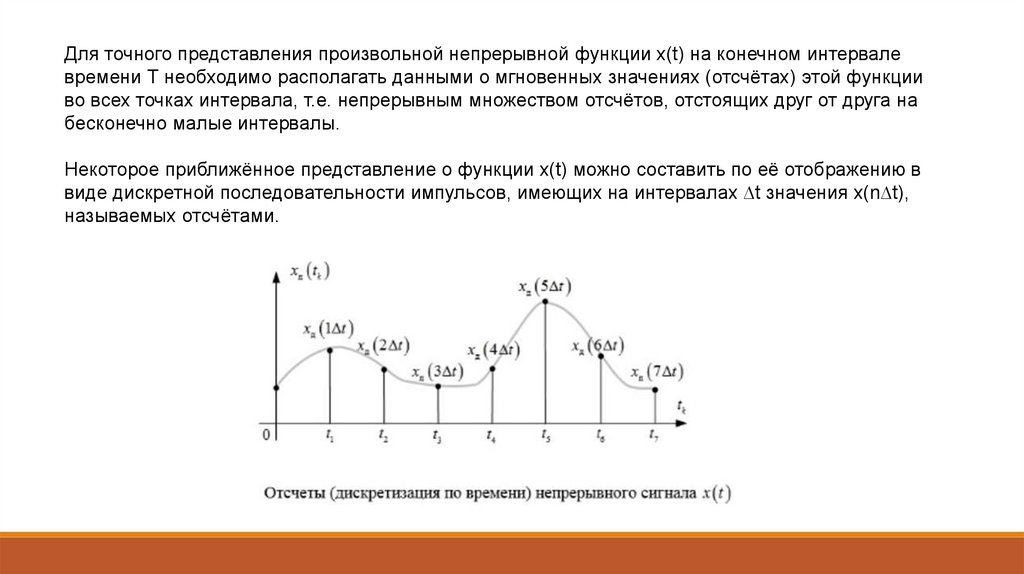
ЦОС представляет собой математику, алгоритмы и методы, используемые для
обработки этих сигналов, после того как они были переведены в дискретную форму.
Обработка может содержать в себе несколько задач: улучшение визуального
отображения, распознавание и синтез речи, сжатие данных для их хранения и
передачи и др.

4.

5.

В теории информации под сигналом понимается материальный носитель информации.
В цифровой же обработке сигналов под сигналом будем понимать его математическое
описание, т.е. некоторую вещественную функцию, содержащую информацию о состоянии
или поведении физической системы при каком-нибудь событии, которая может быть
определена на непрерывном или дискретном пространстве изменения времени или
пространственных координат.
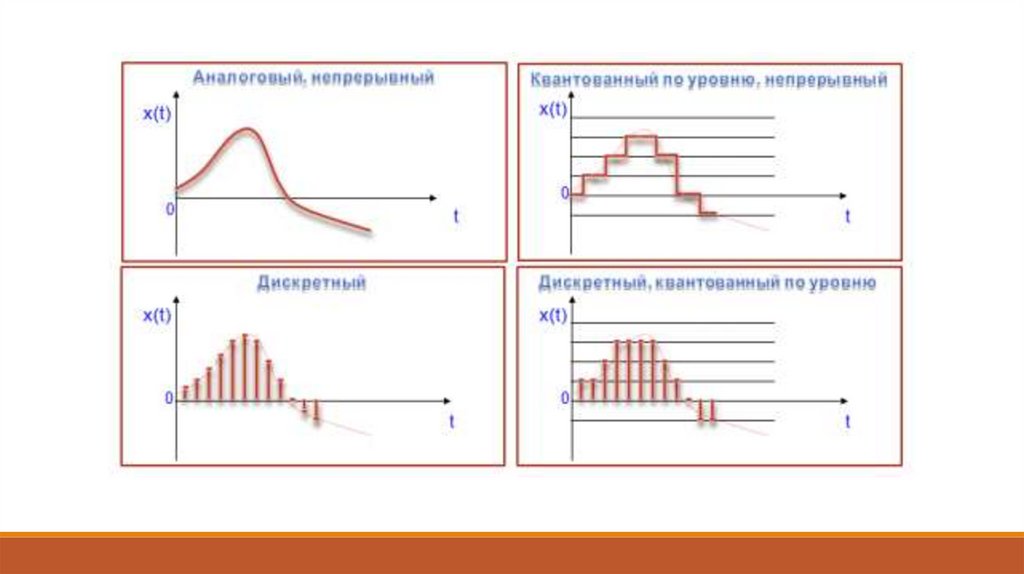
Физические величины макромира, как основного объекта наших измерений и источника
информационных сигналов, как правило, имеют непрерывную природу и отображаются
непрерывными (аналоговыми) сигналами.

6.

7.

Сигнал — это функция, показывающая зависимость одной величины от другой.
Причем эта зависимость должна быть нам чем-то интересна, она должна содержать информацию о
каком-то процессе или явлении.
Например, зависимость давления воздуха в точке от времени можно рассматривать как
звуковой сигнал. Зависимость напряжения в проводнике от времени тоже может
представлять звуковой сигнал. Зависимость яркости точки на плоскости от ее координат
можно рассматривать как черно-белое изображение.
Будем пока для определенности рассматривать одномерные сигналы, зависящие от
времени, и обозначать их x(t). Почти весь материал допускает обобщение и на
многомерный случай.
При
обозначении
непрерывных
сигналов
обычно
используют круглые скобки, например, x(t) и y(t).
При обозначении дискретных сигналов обычно используют
квадратные скобки – x[n], y[n] и т.д.

8.

Обработка сигналов — это их преобразование в другие сигналы или в числовые значения
— как правило, для того, чтобы извлечь из них какую-то полезную информацию.
Например, при телефонном разговоре мы хотим по возможности очистить голос собеседника от
посторонних шумов, а принимая сигнал, излучаемый навигационным спутником Глонасс или GPS,
хотим узнать момент его прихода, чтобы измерить расстояние до спутника и благодаря этому
определить свои координаты.
Исходно обработка электрических сигналов осуществлялась электрическими цепями, состоящими из
резисторов, конденсаторов, катушек индуктивности и электронных приборов — сначала ламп, а
затем транзисторов. При этом разработчику нужно было пытаться как-то приспособить физические
свойства этих элементов для того, чтобы приближенно выполнить необходимые операции над
сигналами.

9.

Но в середине двадцатого века произошла революция: появились компьютеры, которые могли
быстро выполнять математические операции над числами. Тогда-то и появилась принципиально
новая концепция: вместо того, чтобы считать сигнал непрерывной функцией, мы представляем его в
виде последовательности чисел, а обработка такого сигнала становится набором математических
операций, выполняемых над этими числами с помощью какого-либо вычислительного устройства. Так
родилась цифровая обработка сигналов, при которой нам уже не нужно как-то приспосабливаться к
физическим свойствам электронных приборов — мы просто берем последовательность чисел и
делаем с ней то, что хотим.

10.

Мы будем в большей степени заниматься анализом сигналов.
Основной целью анализа является сравнение сигналов друг с другом для выявления их сходства и
различия.
Можно выделить три основных составляющих анализа сигналов:
• измерение числовых параметров сигналов; к таким параметрам прежде всего относятся энергия,
средняя мощность и среднеквадратичное значение;
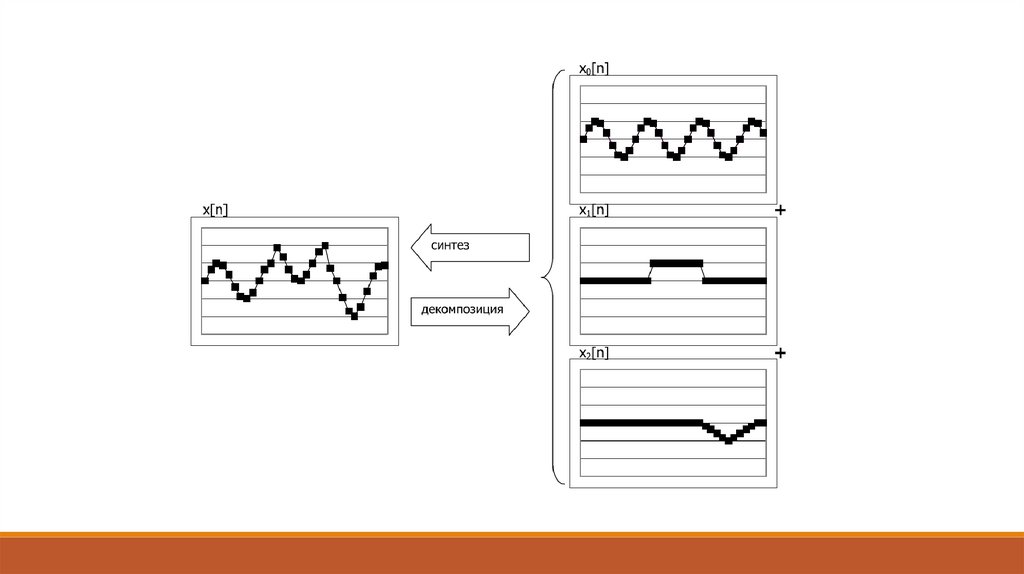
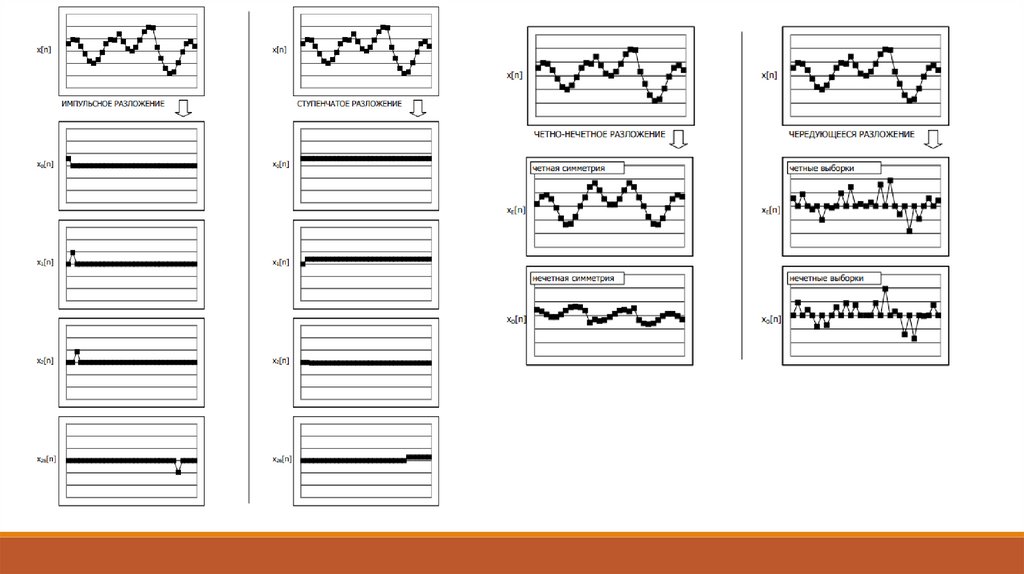
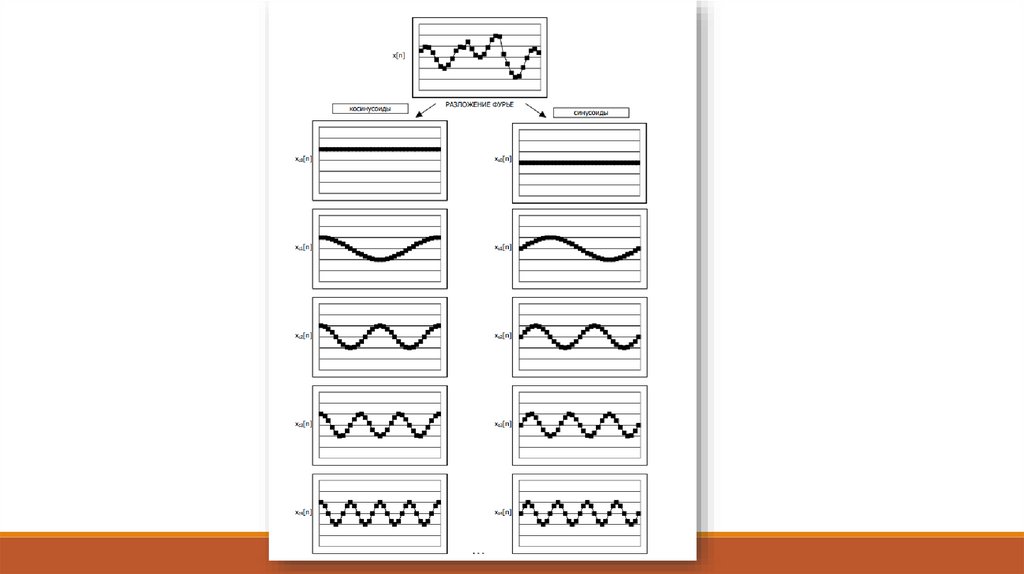
• разложение сигнала на элементарные составляющие для их рассмотрения по отдельности либо
для сравнения свойств различных сигналов. Такое разложение производится с использованием рядов
и интегральных преобразований, важнейшими среди которых являются ряды Фурье и
преобразования Фурье;
• количественное измерение степени «похожести» различных сигналов (корреляционный анализ).

11.

12.

Сигналы
Детерминированные
Периодические
Гармонические
Случайные
Непериодические
Полигармонические
Почти
периодические
Помехи и шумы
Апериодические
Полезные сигналы

13.

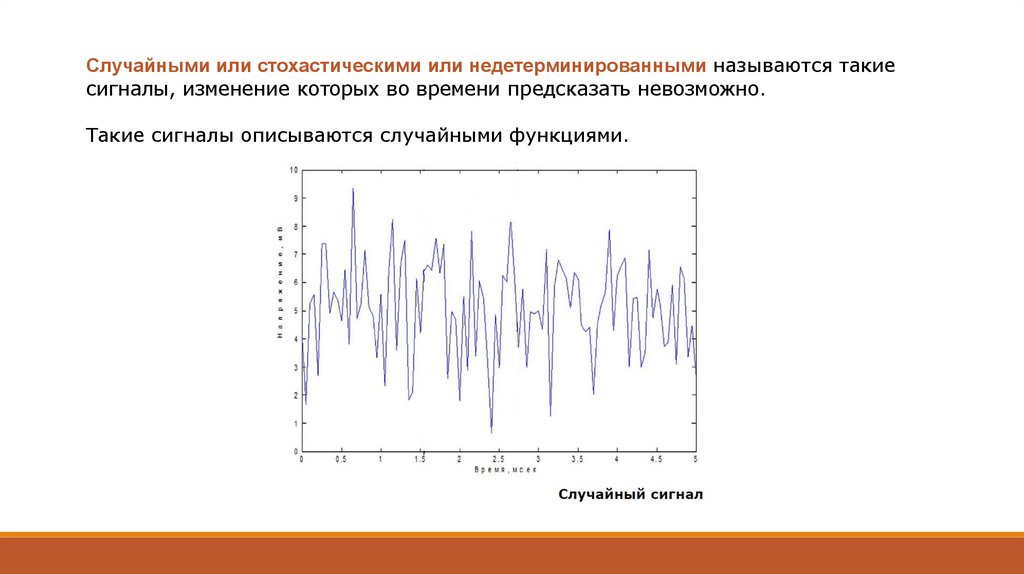
Случайными или стохастическими или недетерминированными называются такие
сигналы, изменение которых во времени предсказать невозможно.
Такие сигналы описываются случайными функциями.

14.

Детерминированными или регулярными называются такие сигналы, значения
которых в любой точке интервала их определения можно рассчитать заранее,
имея математическую модель.
Детерминированные сигналы в чистом виде в природе существовать не могут. Такие сигналы могли
бы возникнуть только в изолированных системах.
Любая же система находится в некоторой среде, и эта среда влияет на процессы, происходящие в
системе. Поэтому детерминированные сигналы являются определенной идеализацией реальных
сигналов.
Математической моделью детерминированного сигнала является детерминированная функция.
Такая модель позволяет для любого заданного момента времени