Похожие презентации:
Решение линейных уравнений и систем. Урок обобщения и систематизации
1.
Урок обобщения и систематизации2. Равенства, которые выполняются при определенных значениях переменной (переменных), называются уравнениями.
• 3х – 1 = 5; х2 – 9 = 0; х2 + у2 = 0 и т.д.Каждое такое значение переменной
(переменных) называют корнем
(решением) уравнения.
Решить уравнение означает, что нужно
найти все его решения или доказать, что их
нет.
3. Для решения линейных уравнений надо:
1. Слагаемые, зависящие от х, перенестив одну часть уравнения, числа – в
другую часть.
2. Привести подобные члены в каждой
части уравнения.
3. Найти неизвестную (переменную) х.
4. Равенство, содержащее две переменные, называют уравнением с двумя переменными (или неизвестными).
Если в уравнение неизвестные входят только впервой степени, то такое уравнение называют
линейным уравнением с двумя переменными.
Линейное уравнение имеет вид ax + by + c = 0.
Решением уравнения с двумя неизвестными
называют пару значений переменных, при
подстановке которых уравнение становится
верным числовым равенством.
5.
6.
1 вариант2 вариант
х=2
х=0
а=1
х=3
х=2
х=0
х=1
х=3
7.
Нас в повседневной жизниокружают системы.
Линейные системы уравнений
8.
Система уравнений – это два и более уравнений. С1.Какую
математическую
модельрешается
называют
помощью
одного уравнения системы
другое, а
в итоге решаются
оба уравнения
системы.
системой
уравнений
с двумя переменными?
2. Что называют решением системы двух
Решением системы уравнений с двумя переменными
линейных
уравнений
с двумя
переменными?
называется
пара значений
переменных,
обращающая
каждое уравнение системы в верное равенство
3. Что значит решить систему уравнений?
Решить систему уравнений - значит найти все
её решения или доказать ,что решений нет
4. Какие методы решения систем уравнений
знаете?
9.
Методы решения системлинейных уравнений
Метод
Графический
подстановки
Метод
сложения
10. Графический метод.
A(0;3)1.Выразить переменную
у из каждого уравнения
системы
D(3;3)
M(2;1)
Y=1
B(3;0)
X=2
C(0;-3)
2. Построить графики
полученных функций
.
3. Найти точки пересечения
графиков
Ответ: (2;1)
11.
2. Решить систему графическим методом2x + y = 5,
4x + 2y = 6
2x + y = 5,
2x + y = 3
у=5-2х
у= 3-2х
12.
Метод подстановкиВыразим у
через х
Подставим
Решим
уравнение
у - 2х=4,
7х - у =1;
у=2х+4,
7х - у=1;
у=6,
х=1.
у=2х+4,
х=1;
Ответ: (1; 6)
у=2х+4,
7х – (2х+4)=1;
7х - 2х - 4 = 1;
5х = 5;
х=1;
Подстави
Подставим
м
13. 3. Решить систему методом подстановки
2x + y = 2,6x – 2y = 4
2x + y = 2,
3x – y = 2
у =2-2х
3х-у =2
3х-2+2х=2
5х=4
х = 0,8 у = 0,4
14.
Метод сложения7х+2у=1,|·( -3)
17х+6у=-9;
1. Если требуется уравнять коэффициенты
при одной из неизвестных переменных в
обоих уравнениях.
-21х-6у=-3,
+
17х+6у=-9;
-----------------21х + 17х = -3 - 9
- 4х = - 12,
х=3;
х=3,
7·3+ 2у =1;
2. Складываем или вычитаем полученные
уравнения
х=3,
21+2у=1;
х=3,
2у=-20;
3. Решить полученное уравнение с одним
неизвестным и найти одну из переменных.
4. Подставить полученное выражение в
любое из двух уравнений системы и решить
это уравнение, получив, таким образом,
вторую переменную.
х=3,
у=-10.
Ответ: (3; - 10)
15. 4.Решить систему уравнений методом сложения (вычитания)
x -2 y = 10,4x – 8y = 40
x - 2y = 10 (4)
4 х - 8у =40
4х-8у=40,
4х - 8у=40
16.
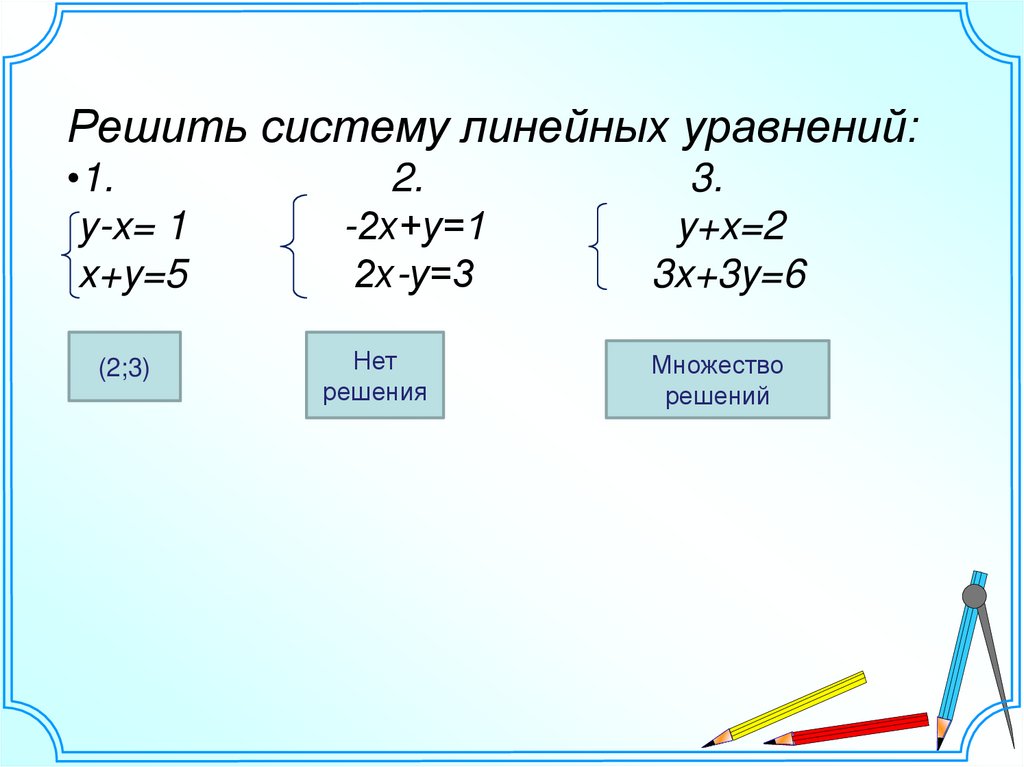
Решить систему линейных уравнений:•1.
y-x= 1
x+y=5
(2;3)
2.
-2х+у=1
2х-у=3
Нет
решения
3.
y+x=2
3x+3y=6
Множество
решений
17.
1.Зависит решение системы от методарешения?
Решение системы не зависит от метода
решения.
2. Сколько решений может иметь система
линейных уравнений
Система линейных уравнений может
иметь одно решение, бесконечно
много решений или вообще не иметь
решений.
18.
Верно ли?1. Решение системы линейных уравнений зависит от
метода решения. нет
2. Система линейных уравнений может иметь
бесконечно много решений. да
3. Системы линейных уравнений могут иметь два
нет
решения.
4. Пара чисел (6; 1) является решением системы
уравнений
х–у=5
да
х + у =7
5.Система линейных уравнений имеет одно решение.
5х-у=4
нет
5х –у=10


















 Математика
Математика








