Похожие презентации:
История появления известных чисел: числа Гугол и Гуголплекс, числа Эйлера, числа Пи
1.
ИСТОРИЯ ПОЯВЛЕНИЯ ИЗВЕСТНЫХЧИСЕЛ: ЧИСЛА ГУГОЛ И
ГУГОЛПЛЕКС, ЧИСЛА ЭЙЛЕРА,
ЧИСЛА ПИ
Работу выполнил студент
группы: Б-3101
Штойко С.С
2.
ИСТОРИЯ ПОЯВЛЕНИЯ ЧИСЛА ГУГОЛ ИГУГОЛПЛЕКС
История появления
О "гуголе" впервые написали в 1938 году в статье "New
Names in Mathematics" в январском номере журнала
Scripta Mathematica американский математик Эдвард
Каснер (Edward Kasner). По его словам, назвать
"гуголом" большое число предложил его девятилетний
племянник Милтон Сиротта (Milton Sirotta).
Общеизвестным же это число стало благодаря,
названной в честь него, поисковой машине Google.
Следует помнить, что "Google" — это торговая марка, а
googol — число.
3.
ГУГОЛ КАК ЧИСЛОКак и все степени 10, гугол имеет только два простых делителя — 2 и 5. Общее количество
целых делителей числа гугол превосходит 10 тыс.[2]
Двоичное представление гугола состоит из 333 бит, из которых последние 100 цифр — нули:
0001 0010 0100 1001 1010 1101 0010 0101 1001 0100 1100 0011 0111 1100 1110 1011 0000 1011
0010 0111 1000 0100 1100 0100 1100 1110 0000 1011 1111 0011 1000 1010 1100 1110 0100
0000 1000 1110 0010 0001 0001 1010 0111 1100 1010 1010 1011 0010 0100 0011 0000 1000
1010 1000 0010 1110 1000 1111 0001 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000
0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 2
Запись в шестнадцатеричной системе гугола состоит из 84 символов, из которых последние 25
цифр — нули:
1249 AD25 94C3 7CEB 0B27 84C4 CE0B F38A CE40 8E21 1A7C AAB2 4308 A82E 8F10 0000
0000 0000 0000 0000 000016
Гугол можно примерно оценить сверху как факториал 70, который превышает гугол примерно
на 20 %:
70! =
11 978 571 669 969 891 796 072 783 721 689 098 736 458 938 142 546 425 857 555 362 864 6
28 009 582 789 845 319 680 000 000 000 000 000 ≈ 1,197857 × 10100
Используя официально принятую в России, США и в ряде других стран систему именования
больших чисел, гугол можно назвать десять дуотригинтиллионов, этимология которого связана
с латинским числительным 32 и означает, что необходимо (32 + 1) раз взять по 3 нуля —
окончание «иллион». Если использовать длинную шкалу, то гугол можно назвать
десять седециллиардов.
4.
ЧИСЛО ГУГОЛПЛЕКСГуголплекс (от англ. googolplex) — число,
равное 10гугол (десяти в степени гугол), то есть 1010100. В
десятичной записи число можно представить как одна
единица и гугол нулей после неё.
Как и гугол, термин «гуголплекс» был придуман
американским математиком Эдвардом
Казнером (англ. Edward Kasner) и его племянником
Милтоном Сироттой (англ. Milton Sirotta).
Число гугол (а тем более, гуголплекс) больше числа
всех частиц в известной нам части вселенной, которое
составляет величину от 1079 до 1081.
5.
МАТЕМАТИЧЕСКИЕ ПРИМЕРЫНаписания со всеми нулями
Гуголплекс = 10^10^100 = 1010 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000
000 000 000 000 000 000 000 000 000 000 000 000 000 000 000
В двоичной системе записывается так:
1 0010 0100 1001 1010 1101 0010 0101 1001 0100 1100 0011 0111 1100 1110
1010^1010^1100100
=
1010
1011 0000 1011 0010 0111 1000 0100 1100 0100 1100 1110 0000 1011 1111 0011 1000 1010 1100 1110 0100 0000 1000 1110
0010 0001 0001 1010 0111 1100 1010 1010 1011 0010 0100 0011 0000 1000 1010 1000 0010 1110 1000 1111 0001 0000
0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000
0000 0000
6.
ЧИСЛО ЭЙЛЕРА (ЧИСЛО Е)Первым формулу опубликовал Роджер Котс, математик родом
из Англии, в научном журнале, издаваемом Лондонским
королевским обществом. Затем, формула была отображена в
книге «Гармония мер», которую издали после смерти автора в 1722 году. Котс не придал ей большого значения и
отобразил среди геометрических построений. Чтоб
полученное Котсом выражение приобрело привычный вид,
необходимо исправить ошибку в знаке и перевести на
современный язык описания математики.
Формулу в привычном для людей виде опубликовал Эйлер в
статье 1740 года. В 1748 году выражение было также
представлено в его книге «Введение в анализ бесконечно
малых». Эйлер доказал формулу на основе бесконечных
разложений составляющих формулы в степенные ряды.
7.
МАТЕМАТИЧЕСКИЕ ПРИМЕРЫФормула Эйлера выражает экспоненту через тригонометрические функции, но
можно получить и обратное преобразование. Применимость её для таких
целей очевидна. Заменяют x на –x. Косинус – чётная функция, синус –
нечётная. В результате замены происходит изменение знака перед синусом.
8.
ЧИСЛО ПИЧто такое число пи
Считается, что первым обозначать число пи буквой
греческого алфавита π (pi) стал британский математик
Уильям Джонс в 1706 году, а популяризировал
обозначение его швейцарский коллега Леонард Эйлер в
1737 году. Есть версия, что эта буква выбрана не
случайно, а как начальная в греческом слове perijereia,
что означает «окружность», «периферия».
Число пи — это отношение длины окружности к ее
диаметру. Обозначается оно буквой греческого алфавита
π. Если записать это отношение математическими
символами, то выглядит оно так: π = C/d, где C — это
длина окружности, а d — диаметр окружности. То есть π
— это результат деления длины окружности на ее
диаметр. Но само по себе число пи не является каким-то
параметром окружности.
9.
ЧИСЛО ПИ, ПРИМЕНЕНИЕ В ЖИЗНИЧисло Пи используют многие специалисты в своих
профессиях, такие как: архитекторы, астрономы, физики,
химики и другие.
Число Пи используется не только в математике (периметр),
но и в строительстве башен, плотин и мостов, в астрономии
— для вычислений орбиты спутника.
Также в преобразованиях Фурье (применяется во многих
областях науки), для вычисления общей теории
относительности и для множества вычислений в статистике
и квантовой механике.
10.
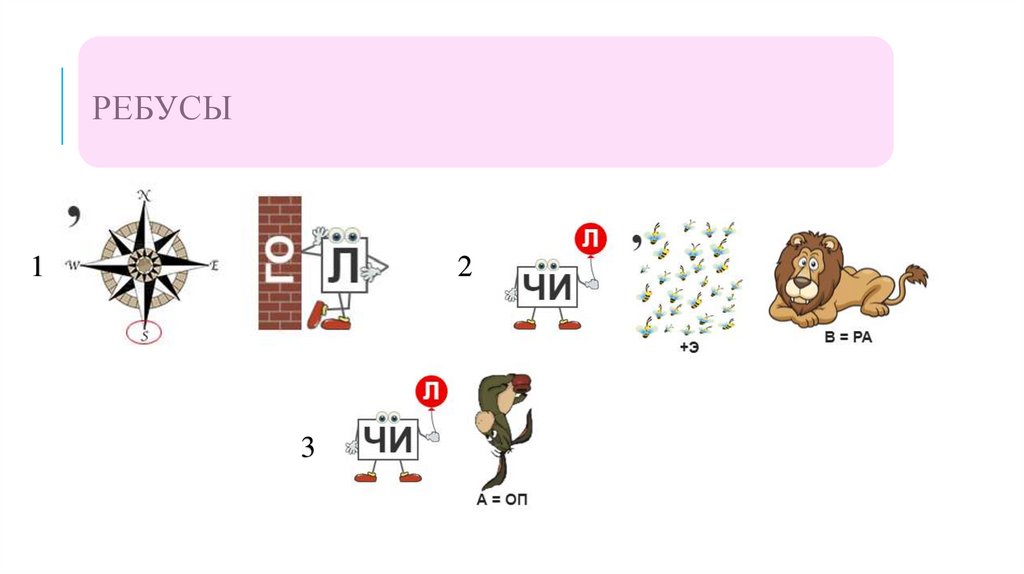
РЕБУСЫ1
2
3
11.
ОТВЕТЫ НА РЕБУСЫ1. Гугол
2. Число эйлера
3. Число пи
12.
ФИЛВОРД13.
гуголгуголплекс
числоэйлера
числопи
число
частица
величина
14.
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ1. Гугол. — Текст : электронный // Академик : [сайт]. — URL: https://dic.academic.ru/dic.nsf/ruwiki/5196 (дата
обращения: 11.09.2023).
2. Google - факт о котором знает не каждый. — Текст : электронный // Статьи : [сайт]. — URL:
https://dzen.ru/a/XbxwlsBccQCufYxJ?utm_referer=www.yandex.ru (дата обращения: 11.09.2023).
3. Гуголплекс. — Текст : электронный // https://googology.fandom.com/ru : [сайт]. — URL:
https://googology.fandom.com/ru/wiki/%D0%93%D1%83%D0%B3%D0%BE%D0%BB%D0%BF%D0%BB%D0
%B5%D0%BA%D1%81 (дата обращения: 11.09.2023).
4. Гуголплекс. — Текст : электронный // Википедия : [сайт]. — URL:
https://ru.wikipedia.org/wiki/%D0%93%D1%83%D0%B3%D0%BE%D0%BB%D0%BF%D0%BB%D0%B5%D0
%BA%D1%81 (дата обращения: 11.09.2023).
5. Число Эйлера. — Текст : электронный // Википедия : [сайт]. — URL:
https://ru.wikipedia.org/wiki/E_(%D1%87%D0%B8%D1%81%D0%BB%D0%BE) (дата обращения: 11.09.2023).
6. Формула Эйлера - доказательство, применение и примеры решения Источник:
https://nauka.club/matematika/formula-eylera.html. — Текст : электронный // https://nauka.club/ : [сайт]. — URL:
https://nauka.club/matematika/formula-eylera.html (дата обращения: 11.09.2023).
7. Число Пи. — Текст : электронный // https://www.kp.ru/edu/ : [сайт]. — URL:
https://www.kp.ru/edu/shkola/chislo-pi/ (дата обращения: 11.09.2023).













 Математика
Математика Информатика
Информатика








