Похожие презентации:
Динамика движения материальной точки по окружности. Тяготение
1.
Динамика движенияматериальной точки по
окружности. Тяготение.
1
2.
23.
34.
45.
56.
67.
78.
89.
910.
1011.
1112.
1213.
1314.
1415.
1516.
Сила упругости16
17.
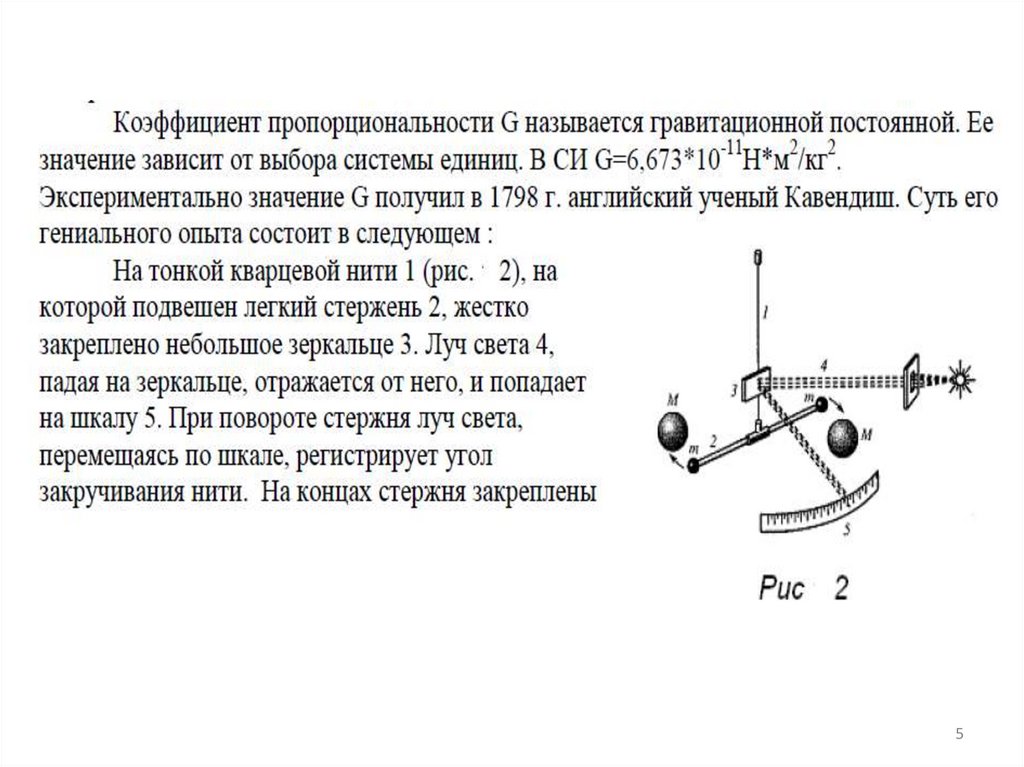
FупрСила упругости – сила, возникающая при
деформации тела и направленная
противоположно направлению смещения
частиц при деформации
mg
17
18.
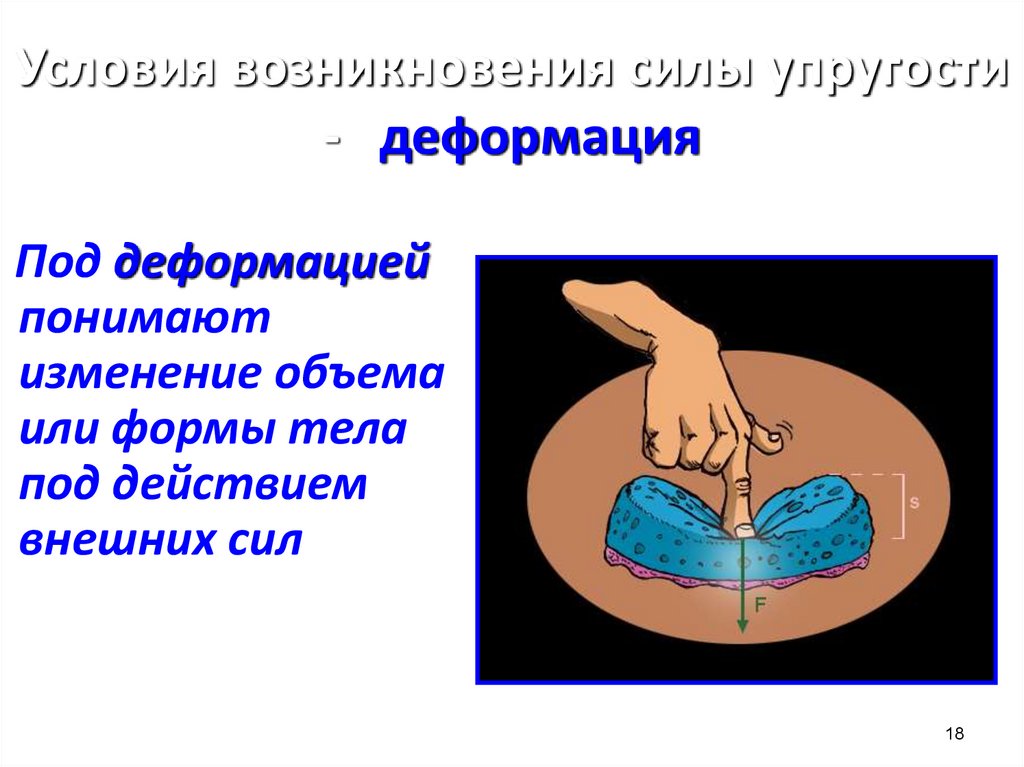
Условия возникновения силы упругости- деформация
Под деформацией
понимают
изменение объема
или формы тела
под действием
внешних сил
18
19.
С целью упрощения расчетов используются следующиедопущения
о
свойствах
материала.
1. Материал считается однородным, если его
свойства
во
всех
точках
одинаковы.
2. Материал считается изотропным, если его свойства
во
всех
направлениях
одинаковы.
3. Материал обладает свойством идеальной упругости,
вследствие которой деформируемое тело полностью
восстанавливает свою форму и размеры после снятия
нагрузки независимо от величин нагрузок и температуры
тела.
4. Материал обладает свойством сплошности, то есть
способностью сплошь (без пустот) заполнять пространство,
ограниченное
поверхностью тела. Вследствие этого материал считается
непрерывным, что позволяет использовать для определения
напряжений и деформаций математический аппарат
дифференциального
и
интегрального
исчисления
.
19
20.
Причины деформацииПри изменении расстояния между атомами изменяются
силы взаимодействия между ними, которые стремятся
вернуть тело в исходное состояния. Поэтому силы
упругости имеют электромагнитную природу.
20
21.
Виды деформацийУпругие –
исчезают после
прекращения
действия внешних
сил:
Растяжения и сжатия
Сдвига
Изгиба
Пластические –
не исчезают после
прекращения
действия внешних
сил
Примеры
деформаций
Кручения
21
22.
Основные типы упругойдеформации
Растяжение
и сжатие
22
23.
Основные типы упругойдеформации
Сдвиг
23
24.
Основные типы упругойдеформации
Изгиб –
сочетание
растяжения и
сжатия
24
25.
Основные типы упругойдеформации
Кручение –
сводится к
сдвигу
25
26.
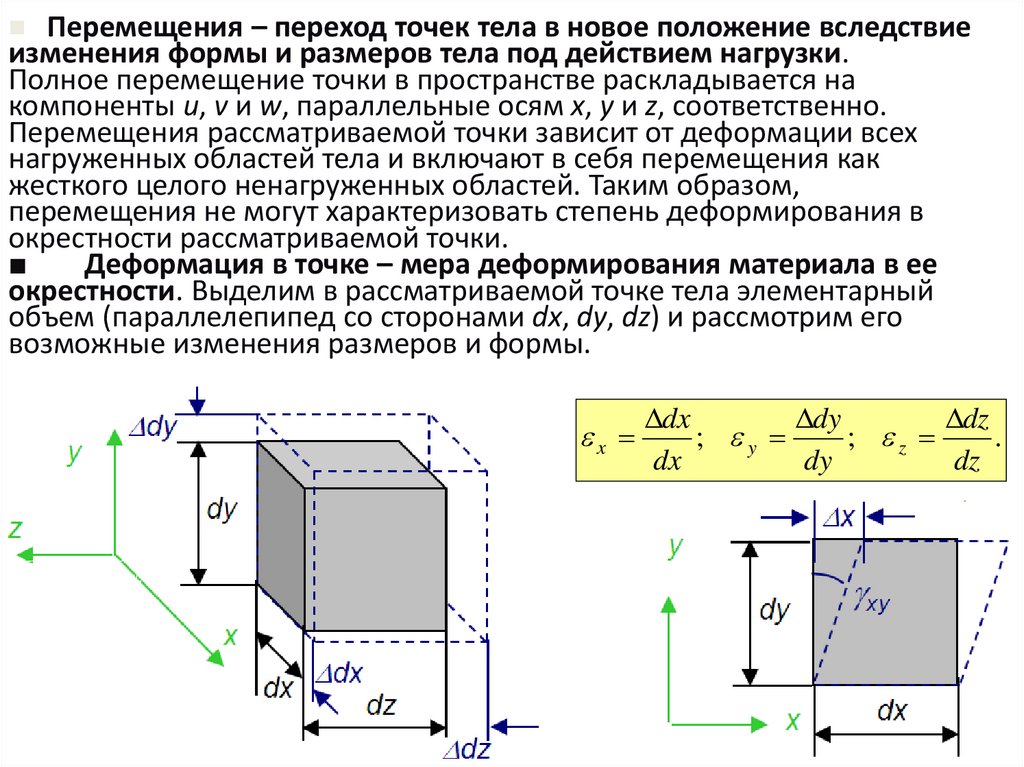
Перемещения – переход точек тела в новое положение вследствиеизменения формы и размеров тела под действием нагрузки.
Полное перемещение точки в пространстве раскладывается на
компоненты u, v и w, параллельные осям x, y и z, соответственно.
Перемещения рассматриваемой точки зависит от деформации всех
нагруженных областей тела и включают в себя перемещения как
жесткого целого ненагруженных областей. Таким образом,
перемещения не могут характеризовать степень деформирования в
окрестности рассматриваемой точки.
■
Деформация в точке – мера деформирования материала в ее
окрестности. Выделим в рассматриваемой точке тела элементарный
объем (параллелепипед со сторонами dx, dy, dz) и рассмотрим его
возможные изменения размеров и формы.
x
dx
dy
dz
; y
; z
.
dx
dy
dz
26
27.
Кроме линейных деформаций, связанных с изменением размеровлинейных элементов возникают угловые деформации или углы сдвига,
связанные с изменением формы. Например, в плоскости xy могут
возникать малые изменения первоначально прямых углов
параллелепипеда:
x
tg xy xy .
dy
Такие угловые деформации в
общем случае могут иметь место
во всех трех плоскостях.
Все относительные деформации весьма малы и имеют для реальных
материалов порядок ≈10-4-10-3.
В зависимости от того, какие из компонент относительных деформаций
Имеют нулевое значение в рассматриваемой области или для всего тела
Различают следующие простые виды деформаций:
1. Линейная деформация – εz ≠ 0, углы сдвига равны нулю, остальными
линейными относительными деформациями пренебрегается
(характеризуется абсолютным и относительным удлинением).
2. Плоская деформация – εz ≠ 0, εx ≠ 0 или εy ≠ 0, остальные относительные
деформации равны нулю (характеризуется абсолютным и относительным
сужением площади поперечного сечения). Эти виды деформаций обычно
реализуются при растяжении-сжатии.
3. Объемная деформация – εz ≠ 0, εx ≠ 0, εy ≠ 0, углы сдвига равны нулю
(характеризуется абсолютным и относительным изменением объема).
4.Чистый сдвиг – линейные относительные деформации равны нулю, углы
cдвига не равны нулю (характеризуется изменением формы, изменение
объема не происходит). Это вид деформации также возникает при
кручении.
27
28.
От чего зависит сила упругости прирастяжении?
Сила упругости зависит от растяжения пружины
28
29.
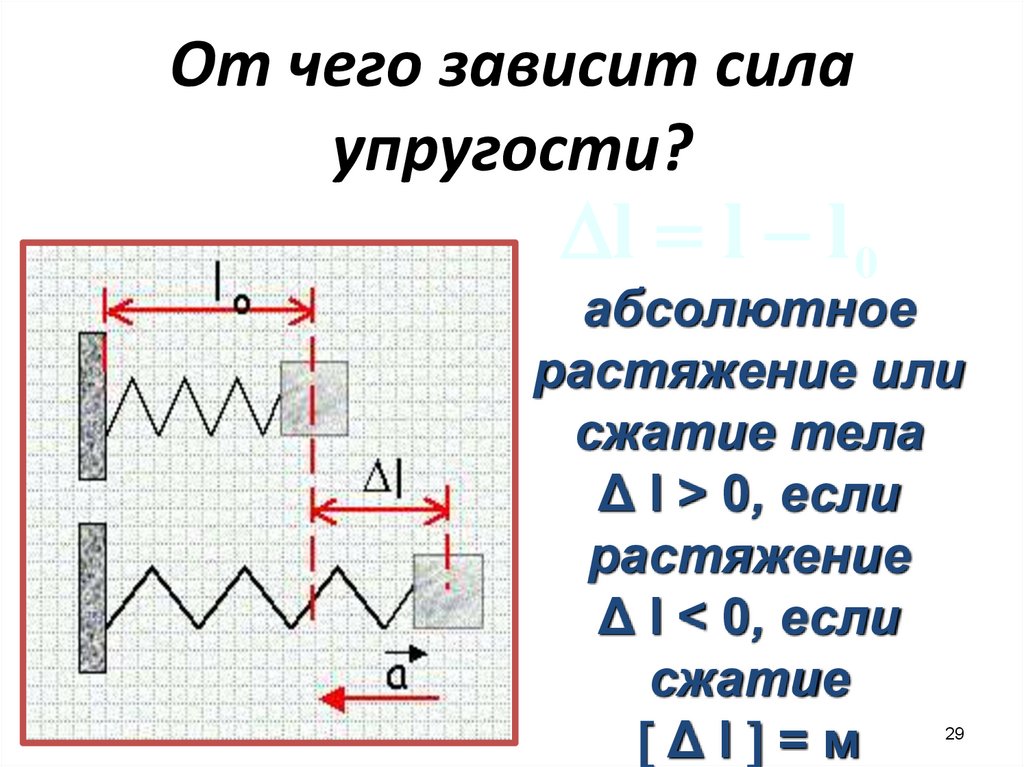
От чего зависит силаупругости?
l l l 0
абсолютное
растяжение или
сжатие тела
Δ l > 0, если
растяжение
Δ l < 0, если
сжатие
Δl =м
29
30.
Сила упругости прямопропорциональна
абсолютному удлинению
(растяжению) тела
F ~ l
30
31.
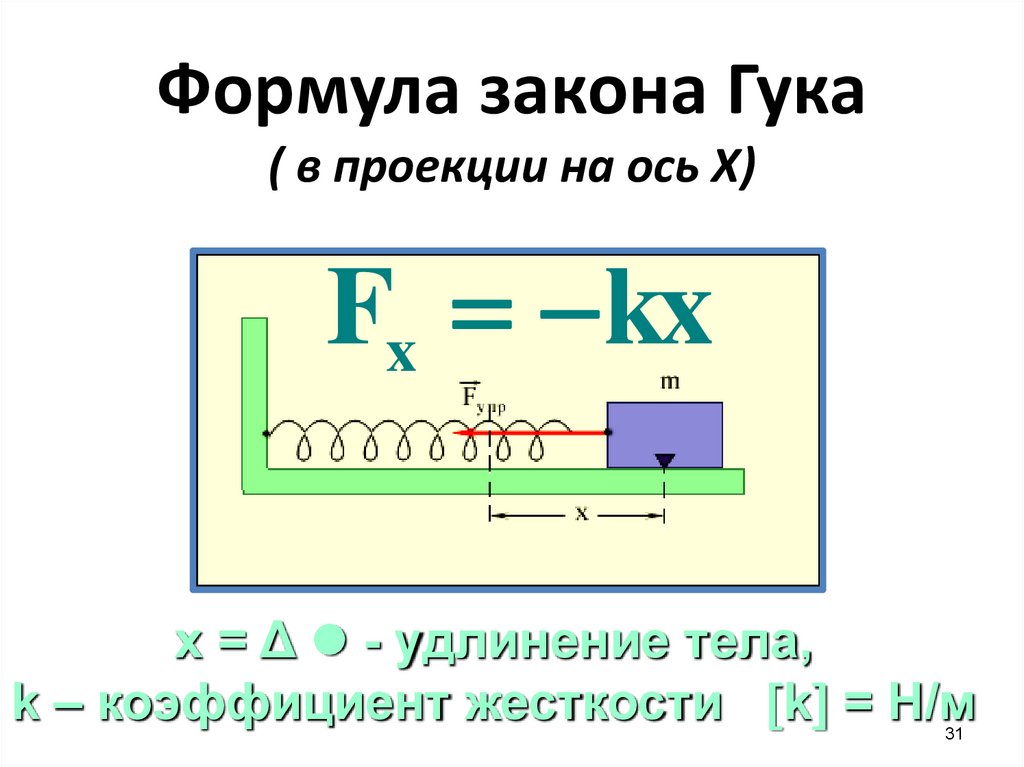
Формула закона Гука( в проекции на ось Х)
Fx kx
х = Δ - удлинение тела,
k – коэффициент жесткости k = Н/м
31
32.
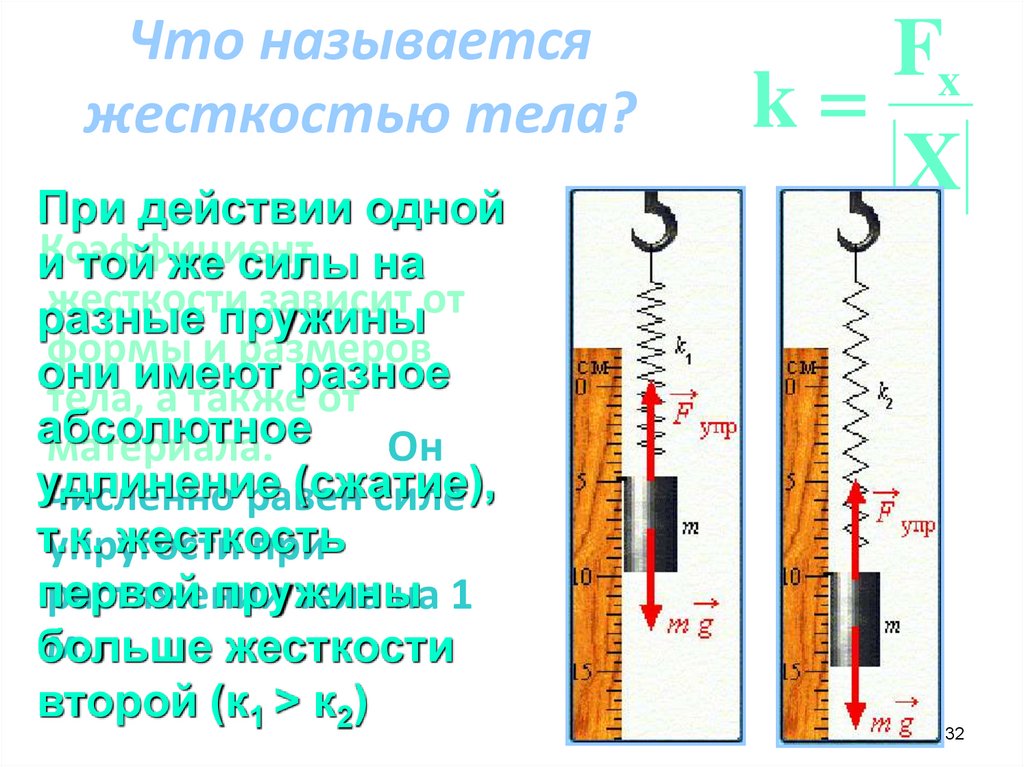
Что называетсяжесткостью тела?
При действии одной
Коэффициент
и
той же силы на
жесткости
зависит от
разные
пружины
формы и размеров
они имеют разное
тела, а также от
абсолютное
материала.
Он
удлинение
(сжатие),
численно равен
силе
т.к.
жесткость
упругости
при
первой
пружины
растяжении
тела на 1
м.
больше
жесткости
второй (к1 > к2)
Fx
k
X
32
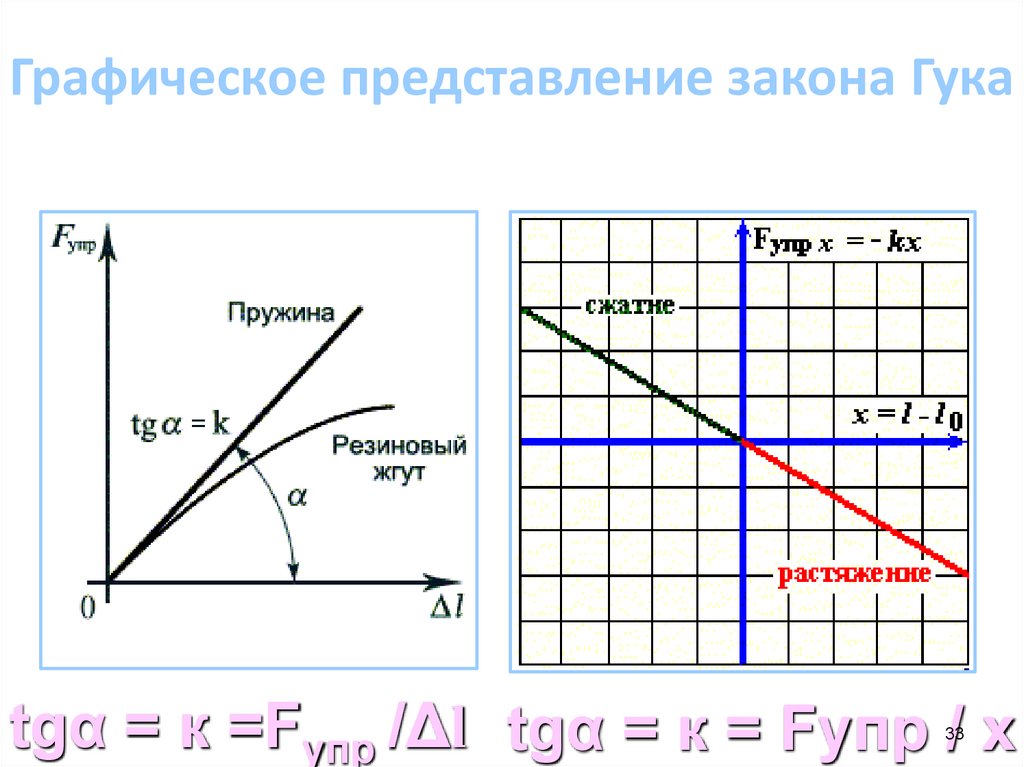
33.
Графическое представление закона Гукаtgα = к =Fупр /Δl tgα = к = Fупр / х
33
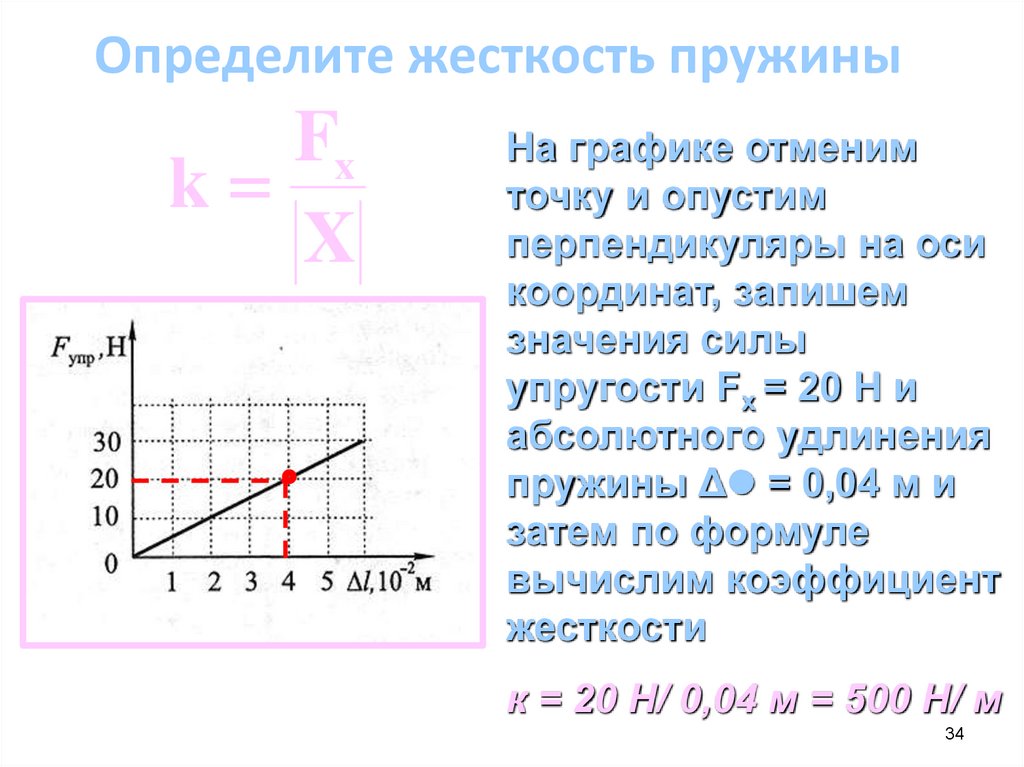
34.
Определите жесткость пружиныFx
k
X
На графике отменим
точку и опустим
перпендикуляры на оси
координат, запишем
значения силы
упругости Fx = 20 Н и
абсолютного удлинения
пружины Δ = 0,04 м и
затем по формуле
вычислим коэффициент
жесткости
к = 20 Н/ 0,04 м = 500 Н/ м
34
35.
Закон Гука для малыхупругих деформаций
Сила упругости, возникающая при
деформации тела, прямо
пропорциональна его удлинению
(сжатию) и направлена
противоположно перемещению
частиц тела при деформации
35
36.
Закон Гука при изгибеЗакон Гука можно обобщить
и на случай более сложной
деформации, например,
деформации изгиба:
сила упругости прямо
пропорциональна прогибу
стержня, концы которого
лежат на двух опорах
36
37.
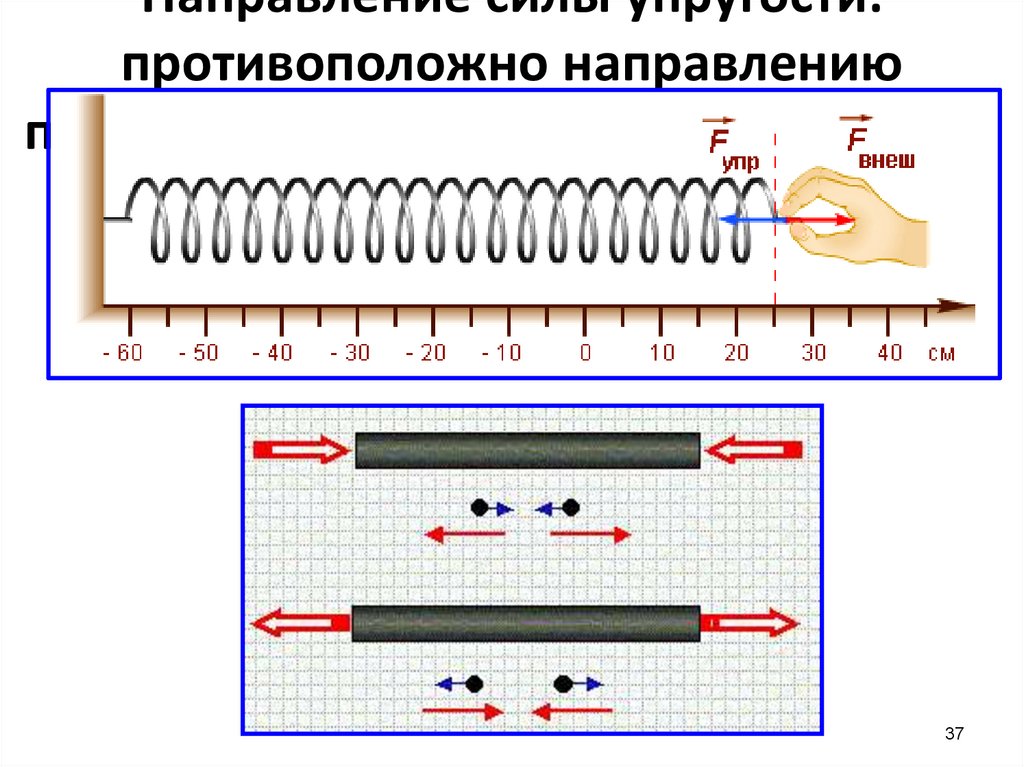
Направление силы упругости:противоположно направлению
перемещения частиц при деформации
37
38.
В физике закон Гука принятозаписывать в другой форме
Для этого введем
две новые
величины:
относительное
удлинение
(сжатие) – ε
и напряжение σ
Относительное удлинение
(сжатие) – это изменение
длины тела, отнесенное к
единице длины. Оно равно
отношению относительного
удлинения тела (сжатия) к его
первоначальной длине:
l
1
l0
38
39.
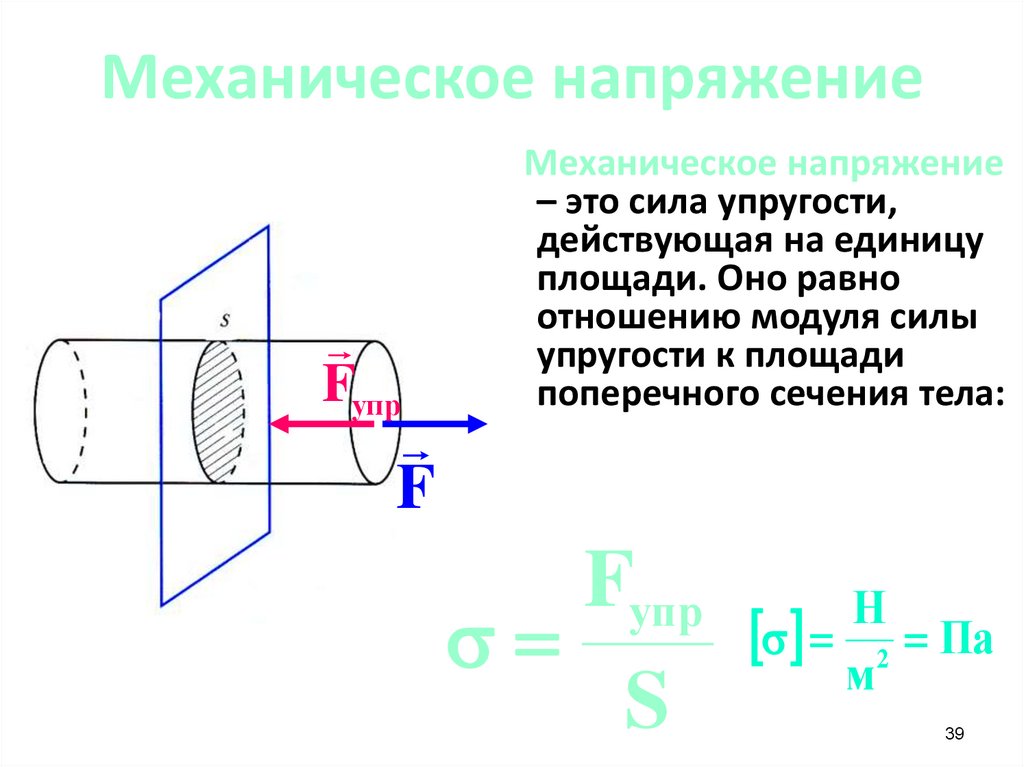
Механическое напряжениеFупр
F
Механическое напряжение
– это сила упругости,
действующая на единицу
площади. Оно равно
отношению модуля силы
упругости к площади
поперечного сечения тела:
Fупр
Н
Па
м
S
2
39
40.
При упругой малой деформациимеханическое напряжение прямо
пропорционально относительному
удлинению (сжатию) тела
E
где Е – модуль Юнга или модуль упругости, который
измеряется в Па ( Е = σ / ε измеряется в тех же
40
единицах, что напряжение)
41.
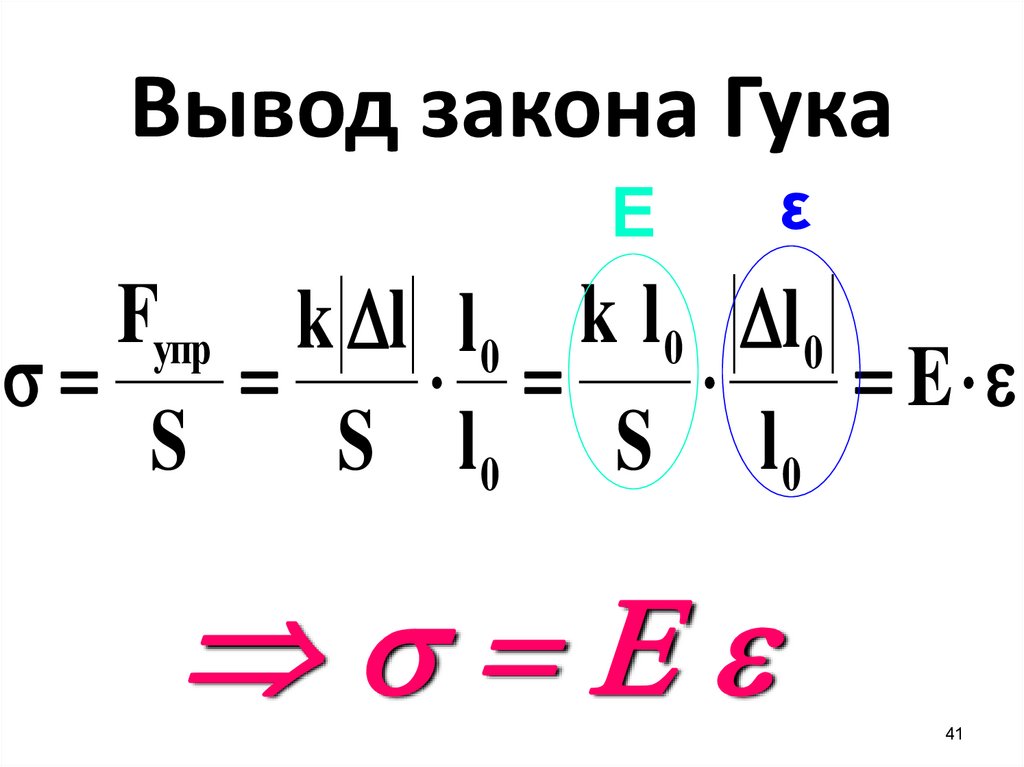
Вывод закона ГукаЕ
ε
Fупр k l l 0 k l 0 l 0
E
S
S l0 S l0
41
42.
Модуль упругости - ЕМодуль Юнга зависит только от свойств
материала и не зависит от размеров и формы
тела.
Модуль Юнга показывает напряжение, которое
необходимо приложить к телу, чтобы удлинить
его в 2 раза.
Для различных материалов модуль Юнга
меняется в широких пределах. Для стали,
например, E ≈ 2·1011 Н/м2, а для резины
E ≈ 2·106 Н/м2.
42
43.
Механические свойства твердых телМеханическая
характеристика
Обозначение
Пояснения
Предел
пропорциональнос
ти
σп
наибольшее напряжение, до которого справедлив закон
Гука
Предел упругости
σуп
наибольшее напряжение, при котором ещё не возникают
заметные остаточные деформации
Предел текучести
σт
напряжение, при котором происходит рост остаточных
деформаций образца при практически постоянной силе
Предел прочности
43
условное напряжение, соответствующее наибольшей
44.
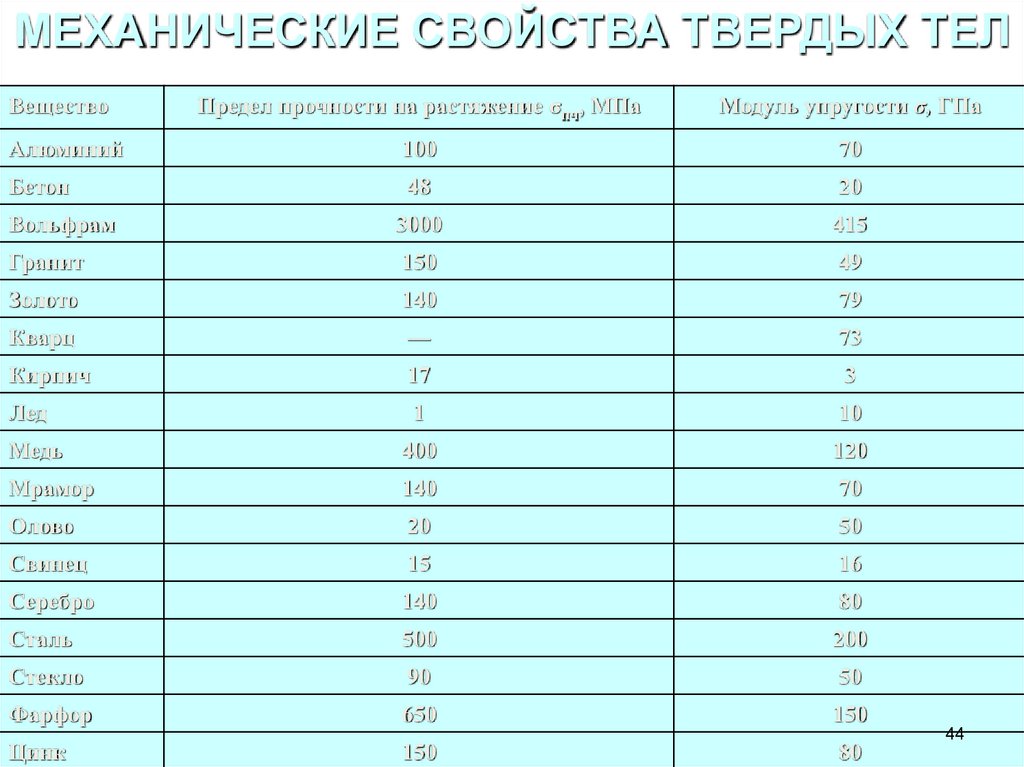
МЕХАНИЧЕСКИЕ СВОЙСТВА ТВЕРДЫХ ТЕЛВещество
Предел прочности на растяжение σпч, МПа
Модуль упругости σ, ГПа
Алюминий
100
70
Бетон
48
20
Вольфрам
3000
415
Гранит
150
49
Золото
140
79
Кварц
—
73
Кирпич
17
3
Лед
1
10
Медь
400
120
Мрамор
140
70
Олово
20
50
Свинец
15
16
Серебро
140
80
Сталь
500
200
Стекло
90
50
Фарфор
650
150
Цинк
44
150
80
45.
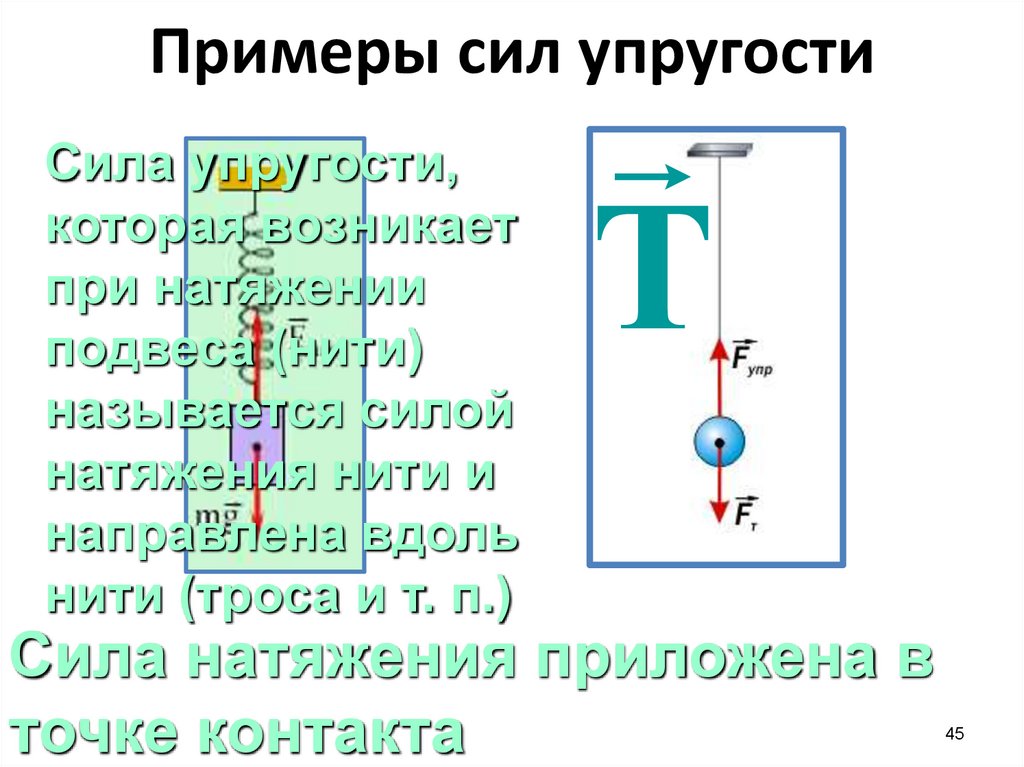
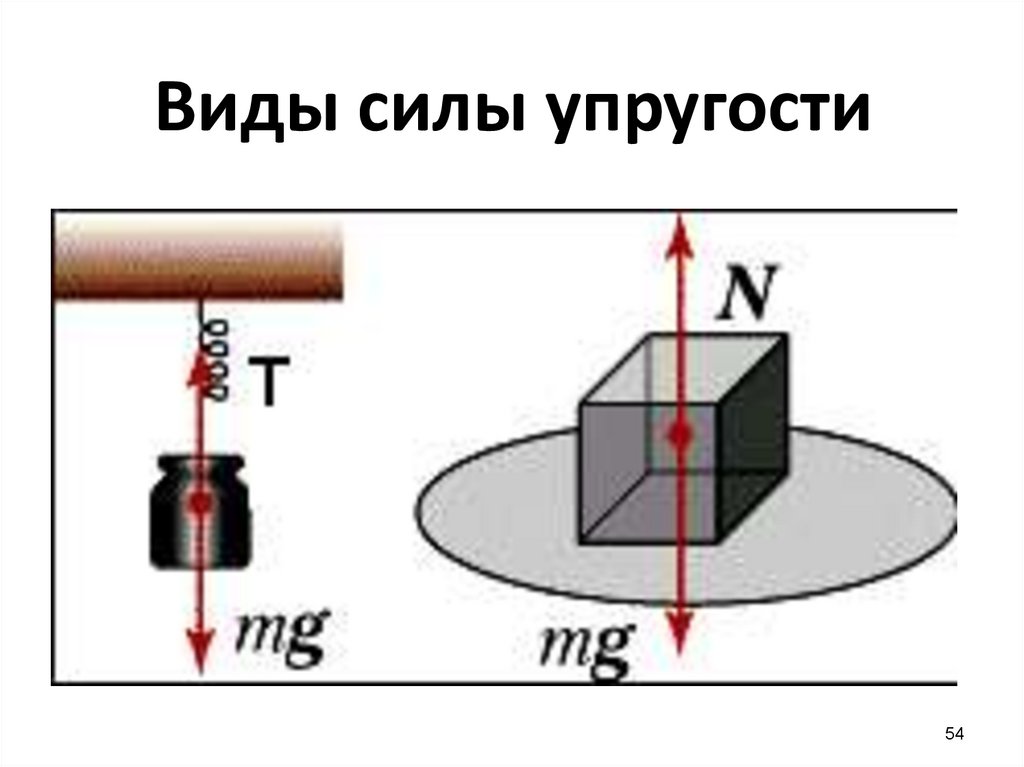
Примеры сил упругостиСила упругости,
которая возникает
при натяжении
подвеса (нити)
называется силой
натяжения нити и
направлена вдоль
нити (троса и т. п.)
Т
Сила натяжения приложена в
точке контакта
45
46.
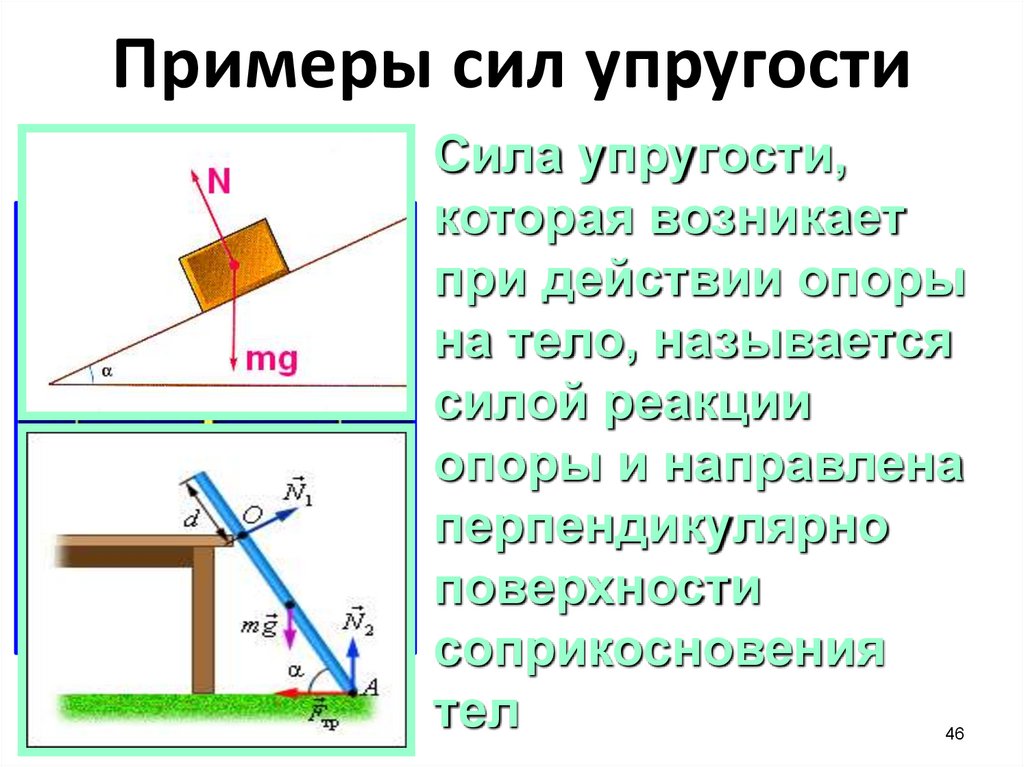
Примеры сил упругостиN
Сила упругости,
которая возникает
при действии опоры
на тело, называется
силой реакции
опоры и направлена
перпендикулярно
поверхности
соприкосновения
тел
46
47.
ДинамометрВ пределах
применимости закона
Гука пружины способны
сильно изменять свою
длину. Поэтому их часто
используют для
измерения сил.
Пружину, растяжение
которой
проградуировано в
единицах силы,
называют
динамометром
47
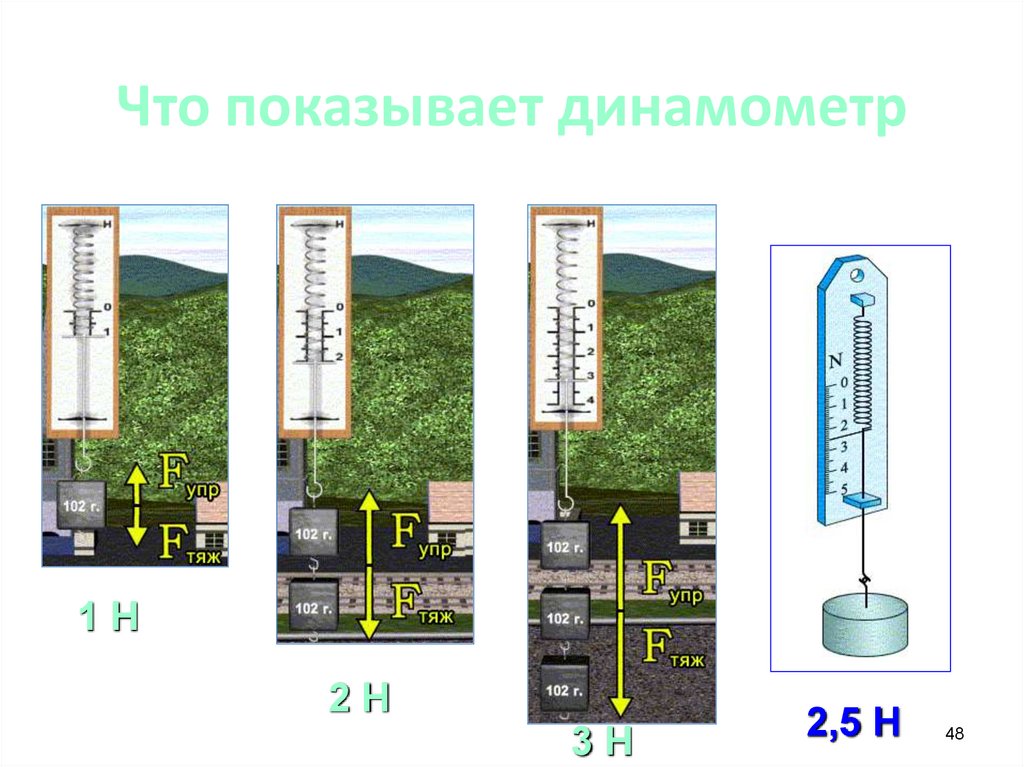
48.
Что показывает динамометр1Н
2Н
3Н
2,5 Н
48
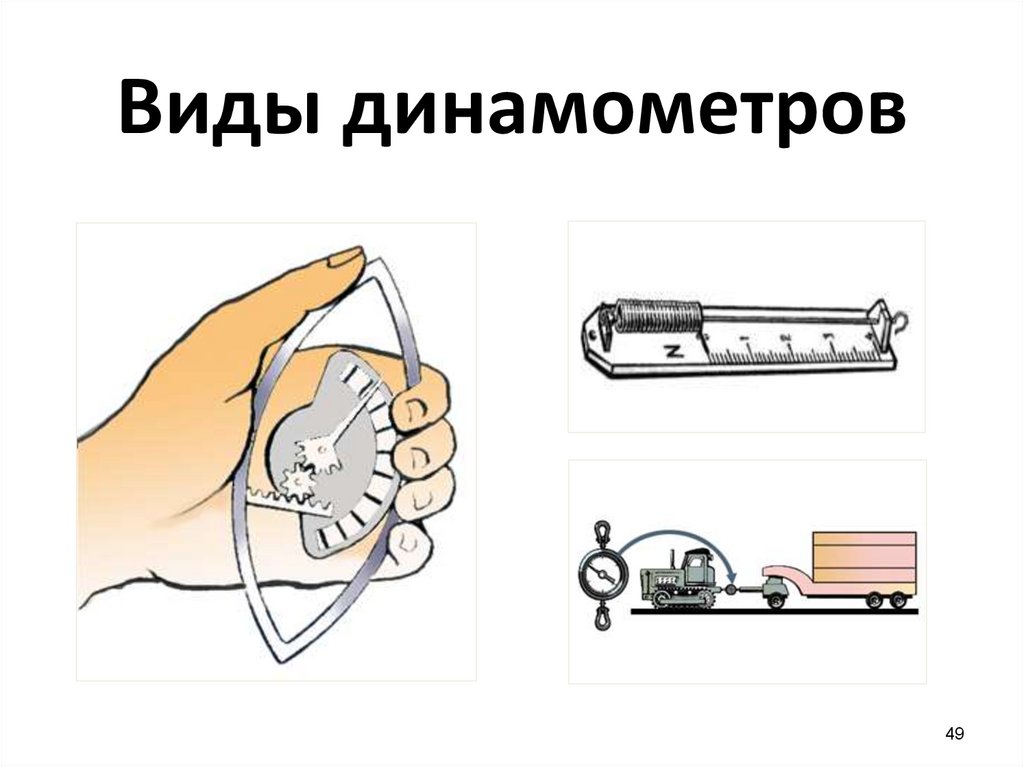
49.
Виды динамометров49
50.
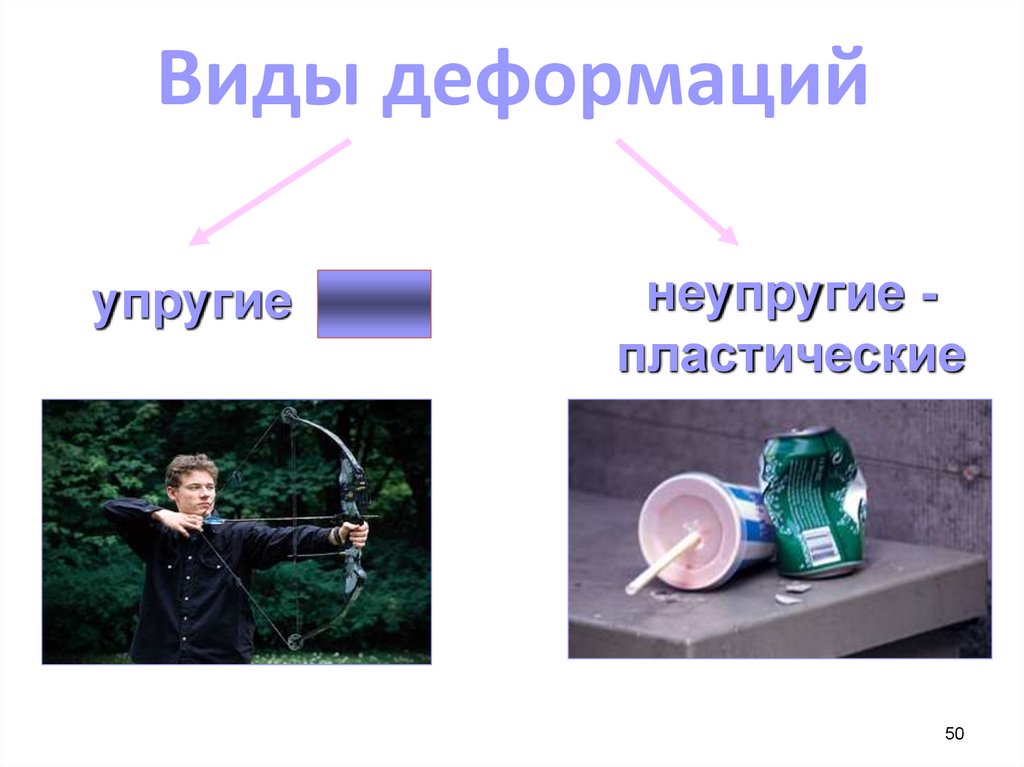
Виды деформацийупругие
неупругие пластические
50
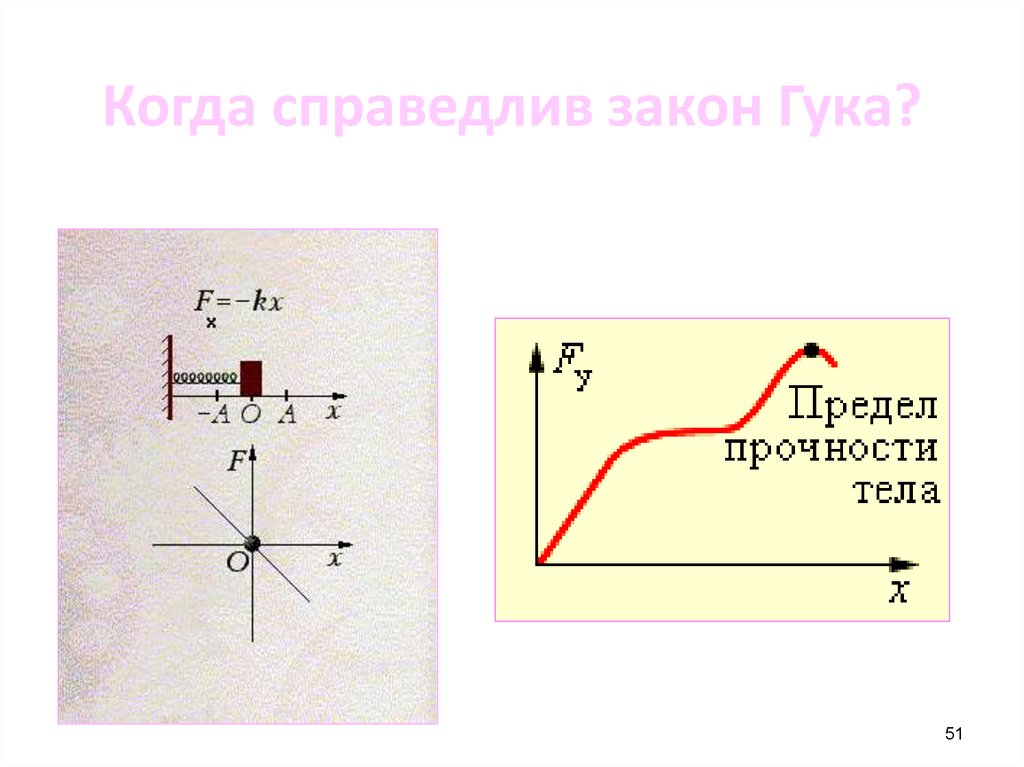
51.
Когда справедлив закон Гука?51
52.
12
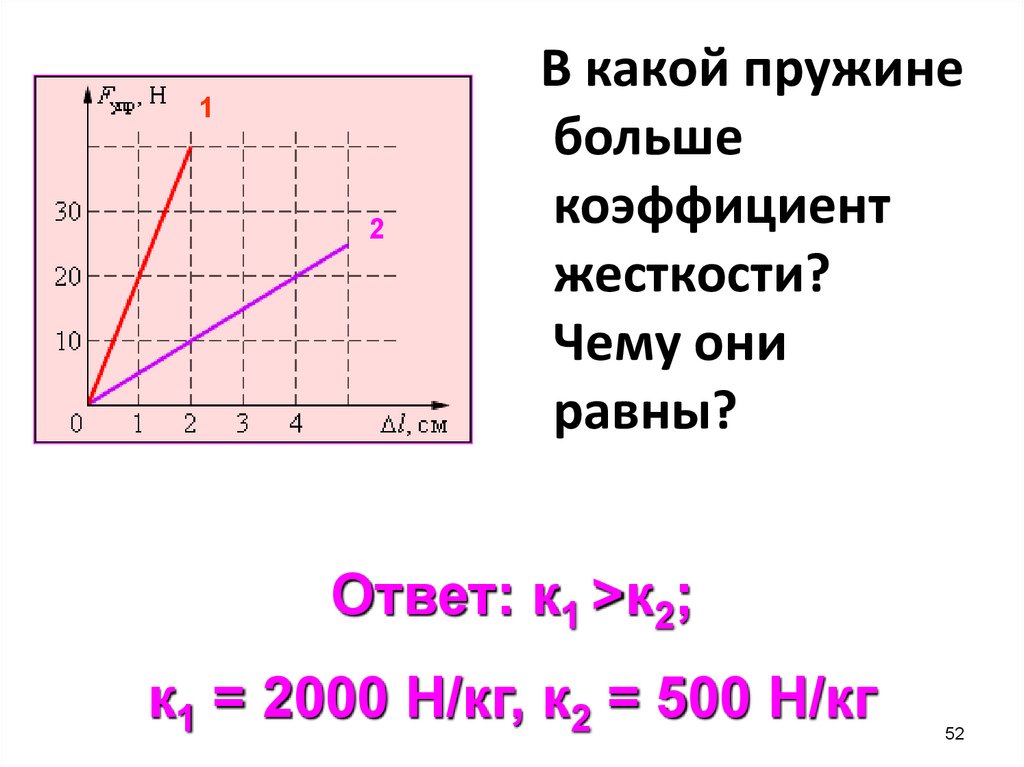
В какой пружине
больше
коэффициент
жесткости?
Чему они
равны?
Ответ: к1 >к2;
к1 = 2000 Н/кг, к2 = 500 Н/кг
52
53.
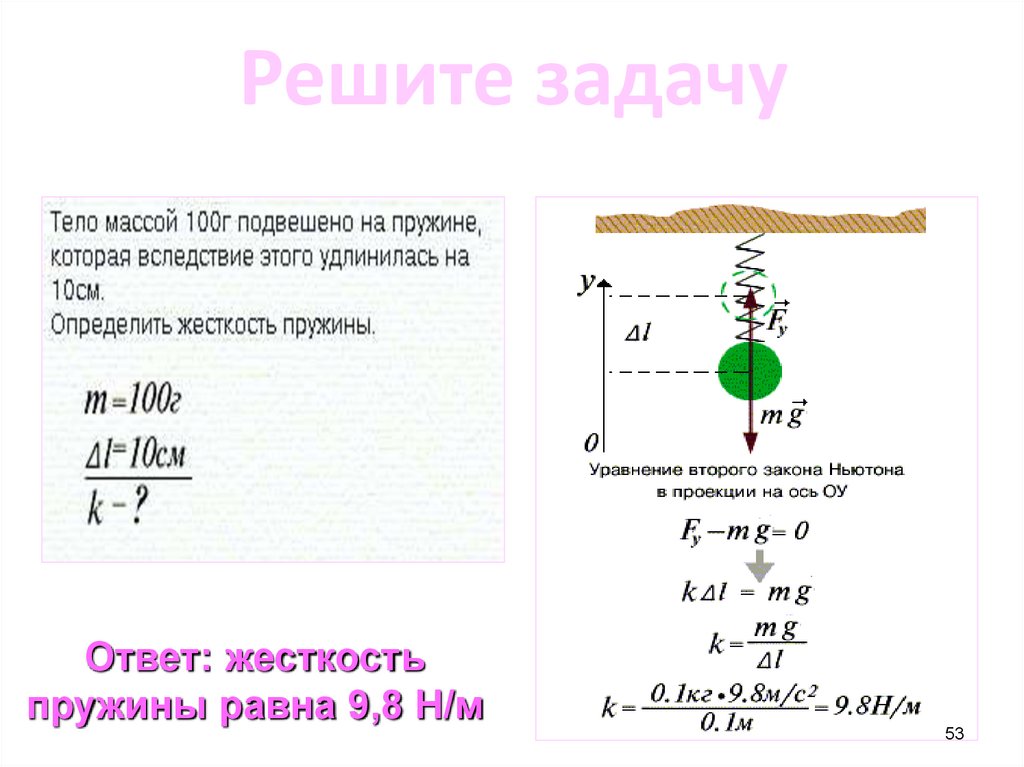
Решите задачуОтвет: жесткость
пружины равна 9,8 Н/м
53
54.
Виды силы упругости54
55.
Какие деформации изображены?55
56.
Деформации в жизни56
57.
Деформации в жизни57
58.
Силы трения58
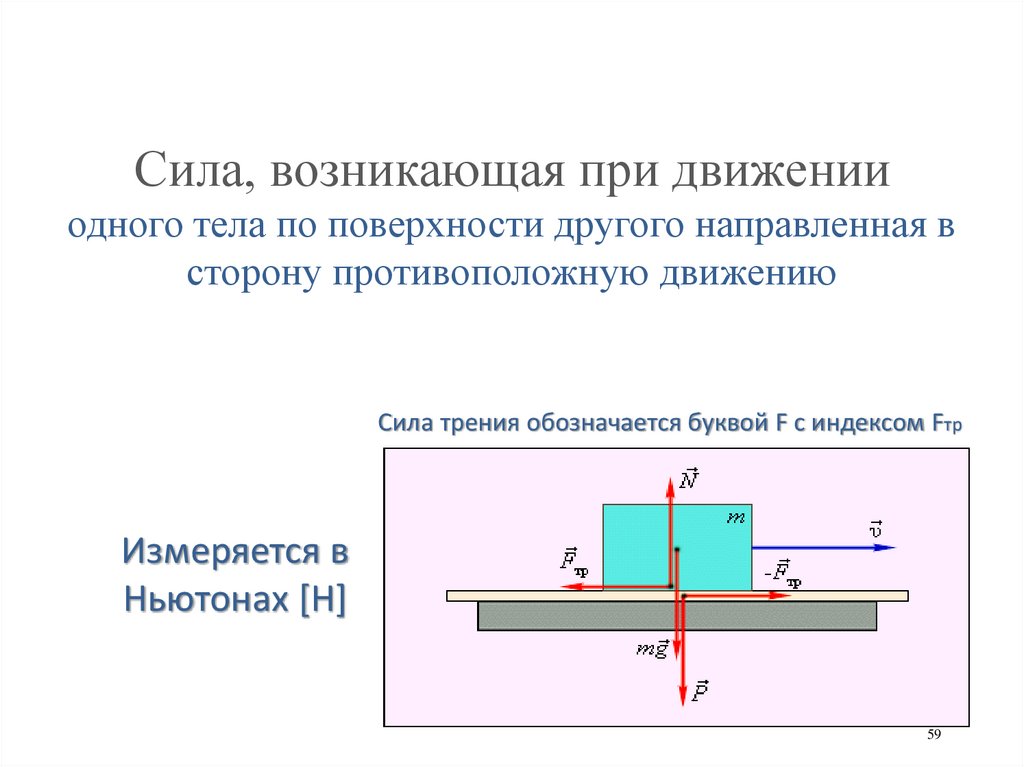
59.
Сила, возникающая при движенииодного тела по поверхности другого направленная в
сторону противоположную движению
Сила трения обозначается буквой F с индексом Fтр
Измеряется в
Ньютонах [H]
59
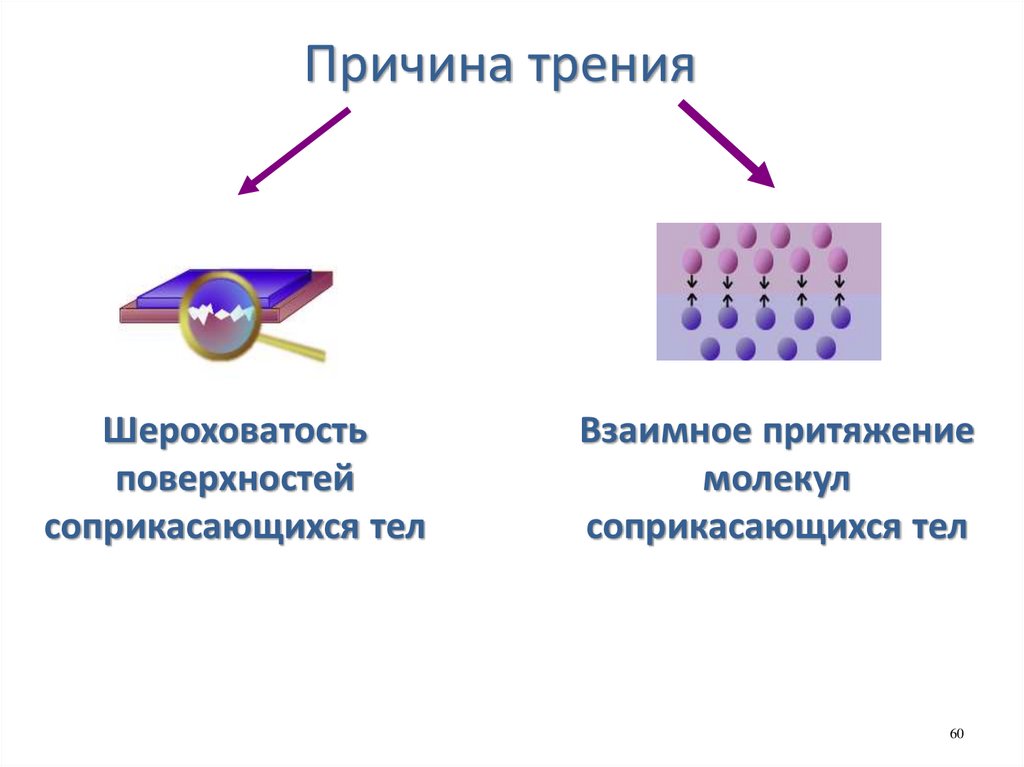
60.
Причина тренияШероховатость
поверхностей
соприкасающихся тел
Взаимное притяжение
молекул
соприкасающихся тел
60
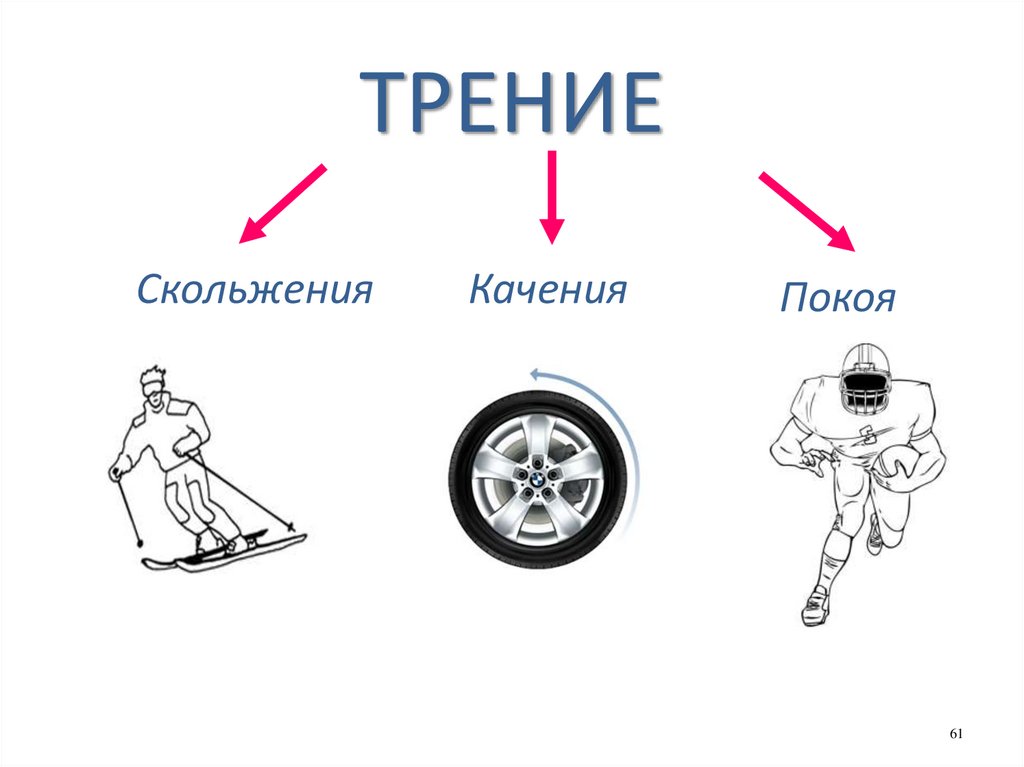
61.
ТРЕНИЕСкольжения
Качения
Покоя
61
62.
■ Трение скольжения. При действии сдвигающей силы,приложенной к телу, покоящемуся на шероховатой поверхности,
возникает сила, противодействующая возможному смещению
тела (сила трения сцепления) из равновесного положения или
его действительному перемещению (сила трения скольжения)
при его движении.
Основные законы трения (Амонтона - Кулона):
1. Сила трения лежит в касательной плоскости к
соприкасающимся поверхностям и направлена в сторону
противоположную направлению, в котором приложенные к телу
силы стремятся его сдвинуть или сдвигают в действительности
(реактивный характер).
2. Сила трения изменяется от нуля до своего максимального
значения 0 Fтр Fтрmax .
Максимальная сила трения
пропорциональна коэффициенту трения и силе нормального
давления Fтрmax fN .
3. Коэффициент трения есть величина постоянная для данного
вида и состояния соприкасающихся поверхностей (f = const).
4. Сила трения в широких пределах не зависит от площади
соприкасающихся поверхностей.
62
63.
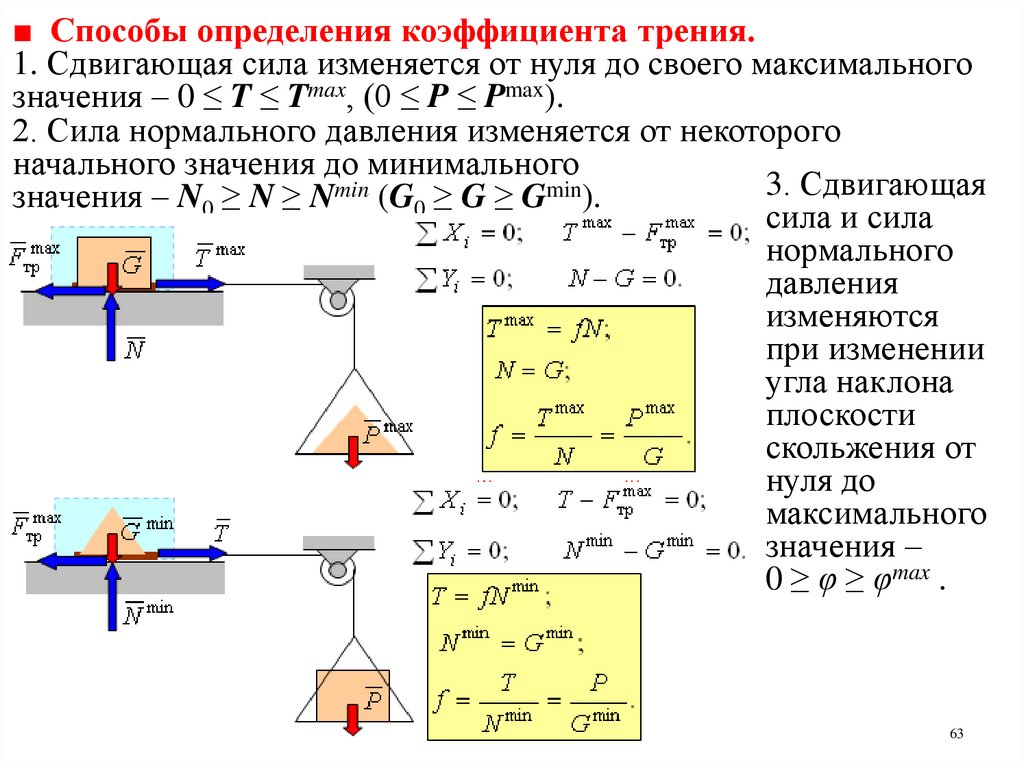
■ Способы определения коэффициента трения.1. Сдвигающая сила изменяется от нуля до своего максимального
значения – 0 ≤ T ≤ Tmax, (0 ≤ P ≤ Pmax).
2. Сила нормального давления изменяется от некоторого
начального значения до минимального
3. Сдвигающая
значения – N0 ≥ N ≥ Nmin (G0 ≥ G ≥ Gmin).
сила и сила
нормального
давления
изменяются
при изменении
угла наклона
плоскости
скольжения от
нуля до
максимального
значения –
0 ≥ φ ≥ φmax .
63
64.
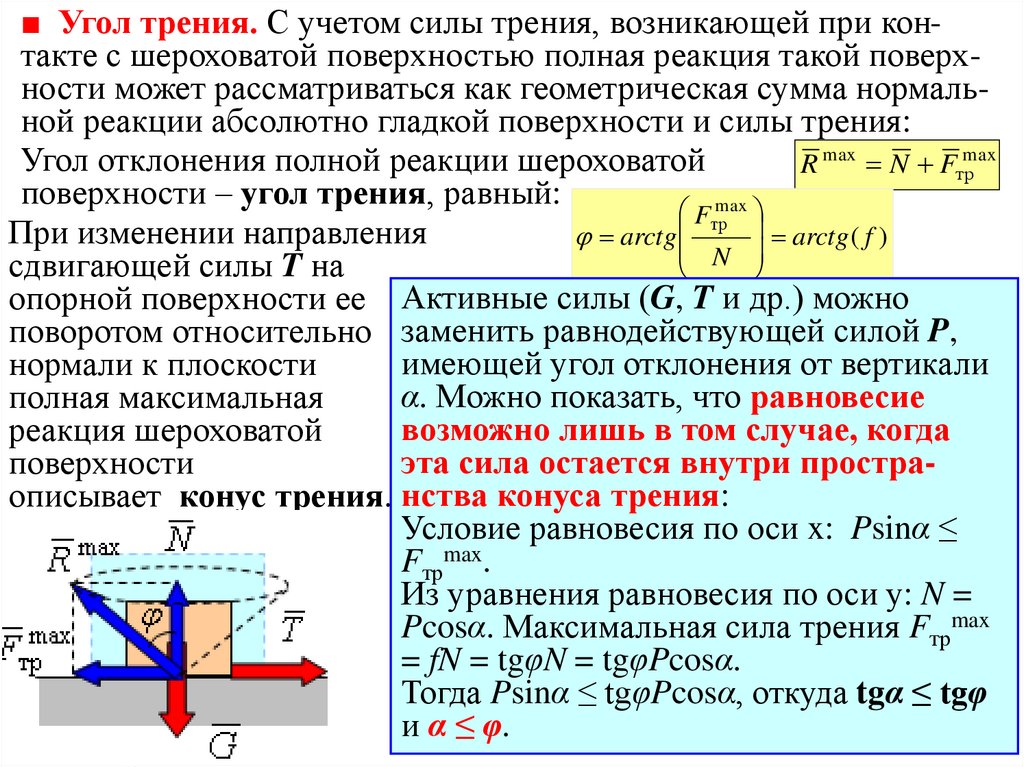
■ Угол трения. С учетом силы трения, возникающей при контакте с шероховатой поверхностью полная реакция такой поверхности может рассматриваться как геометрическая сумма нормальной реакции абсолютно гладкой поверхности и силы трения:Угол отклонения полной реакции шероховатой
R max N Fтрmax
поверхности – угол трения, равный:
Fтрmax
arctg ( f )
При изменении направления
arctg
N
сдвигающей силы T на
опорной поверхности ее Активные силы (G, T и др.) можно
поворотом относительно заменить равнодействующей силой P,
имеющей угол отклонения от вертикали
нормали к плоскости
α. Можно показать, что равновесие
полная максимальная
возможно лишь в том случае, когда
реакция шероховатой
эта сила остается внутри простраповерхности
описывает конус трения. нства конуса трения:
Условие равновесия по оси x: Psinα ≤
Fтрmax.
Из уравнения равновесия по оси у: N =
Pcosα. Максимальная сила трения Fтрmax
= fN = tgφN = tgφPcosα.
Тогда Psinα ≤ tgφPcosα, откуда tgα ≤ tgφ
и α ≤ φ.
64
65.
■ Учет сил трения при решении задач на равновесие. Приналичии сил трения:
1. К действующим на объект активным силам и реакциям
абсолютно гладких поверхностей добавляются
соответствующие силы трения, направленные по общей
касательной к контактным поверхностям в сторону,
противоположную возможному смещению точки касания
объекта относительно опорной шероховатой плоскости.
2. К уравнениям равновесия, составленным для объекта,
добавляются выражения для максимальных сил трения в
количестве, равном числу сил трения.
65
66.
■ Пример решения задачи на равновесие с учетом трения.Человек весом G собирается установить легкую лестницу под
углом α к вертикали (стене) и взобраться на половину длины
лестницы для выполнения работы. Коэффициенты трения в точках
контакта лестницы с полом (A) и со стеной (B) равны fA и fB
соответственно. Определить предельное значение угла наклона,
при котором лестница с человеком может сохранять равновесие.
Весом лестницы пренебречь.
1. Выбираем на объект (человек и лестница), отбрасываем связи
и заменяем их действие реакциями гладкой поверхности.
2. Добавляем активные силы (силу тяжести G).
3. Добавляем силы трения, направленные в сторону,
противоположную возможному перемещению
контактных точек A и B лестницы под действием
приложенной активной силы.
66
67.
4. Составляем X i 0;N B FтрA 0;
уравнения
Yi 0; FтрB G N A 0;
равновесия:
AB
B
M iA 0; G
2
sin Fтр AB sin N B AB cos 0.
5. Добавляем
FтрA f A N A ;
выражения
для сил трения: F B f N ;
тр
B
7. Решение первых двух
уравнений дает выражения
для нормальных реакций:
6. Подстановка последних выражений в
уравнения равновесия с простыми
преобразованиями третьего уравнения
дает :
B
N B f A N A 0;
X i 0;
Yi 0; f B N B G N A 0;
1
2
8. Подстановка выражений для нормальных
реакций в третье уравнение равновесия
приводит к возможности определения
предельного угла наклона α:
M iA 0; G tg f B N B tg N B 0.
G
NA
;
1 f A fB
f AG
NB
.
1 f A fB
tg
2 fA
1 f67A f B
68.
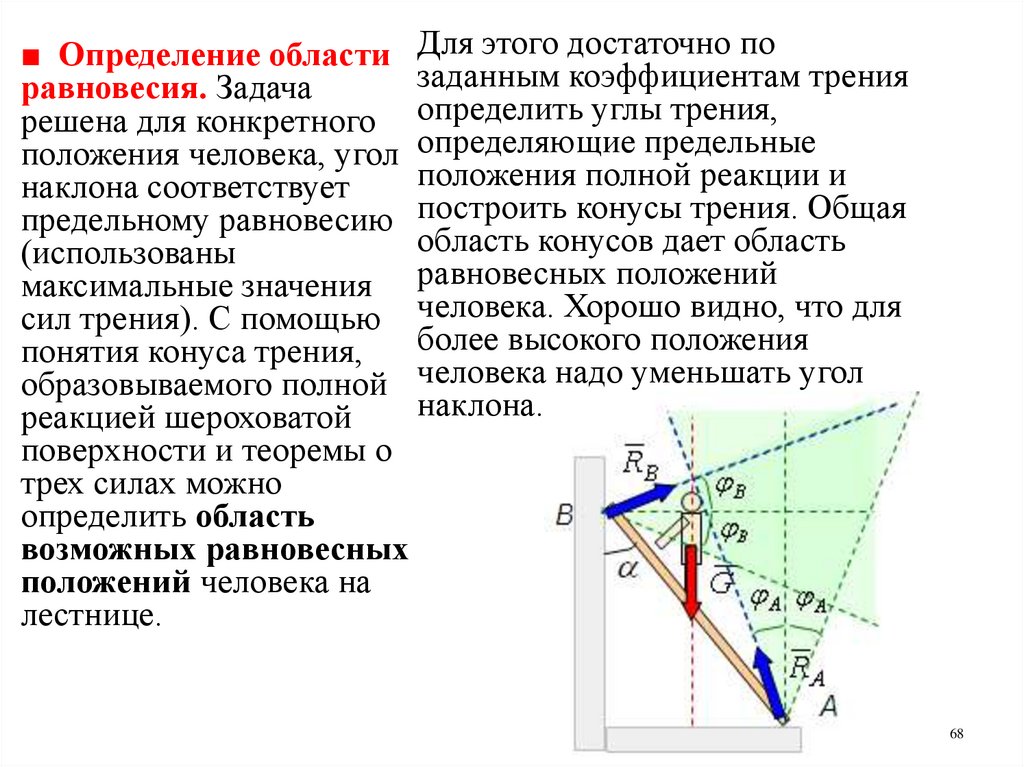
■ Определение области Для этого достаточно позаданным коэффициентам трения
равновесия. Задача
решена для конкретного определить углы трения,
положения человека, угол определяющие предельные
положения полной реакции и
наклона соответствует
предельному равновесию построить конусы трения. Общая
область конусов дает область
(использованы
максимальные значения равновесных положений
сил трения). С помощью человека. Хорошо видно, что для
более высокого положения
понятия конуса трения,
образовываемого полной человека надо уменьшать угол
наклона.
реакцией шероховатой
поверхности и теоремы о
трех силах можно
определить область
возможных равновесных
положений человека на
лестнице.
68
69.
■ Сопротивление при качении. При действии сдвигающейсилы, приложенной к катку, покоящемуся на шероховатой
поверхности, возникает сила, противодействующая возможному
смещению тела (сила трения сцепления) из равновесного
положения или его действительному перемещению (сила трения
скольжения) при его движении и пара сил, момент которой
препятствует повороту катка (момент сопротивления качению).
Возникновение пары сил, препятствующей качению, связана с
деформацией опорной плоскости, в результате которой
равнодействующая нормальных реактивных сил по площадке
контакта смещена от линии действия силы тяжести в сторону
возможного или действительного движения.
69
70.
Основные законы трения качения:1. Момент сопротивления качению всегда направлен в сторону противоположную, тому
направлению, в котором приложенные к телу силы стремятся его повернуть, или
действительному повороту под действием этих сил (реактивный характер).
2. Момент сопротивления качению изменяется от нуля до своего максимального
значения
.
Максимальный момент сопротивления качению пропорционален коэффициенту трения
качения и силе нормального давления:
.
3. Коэффициент трения качения есть величина постоянная для данного вида и состояния
соприкасающихся поверхностей
(fк = const).
4. Момент сопротивления качению в широких пределах не зависит от радиуса катка.
70
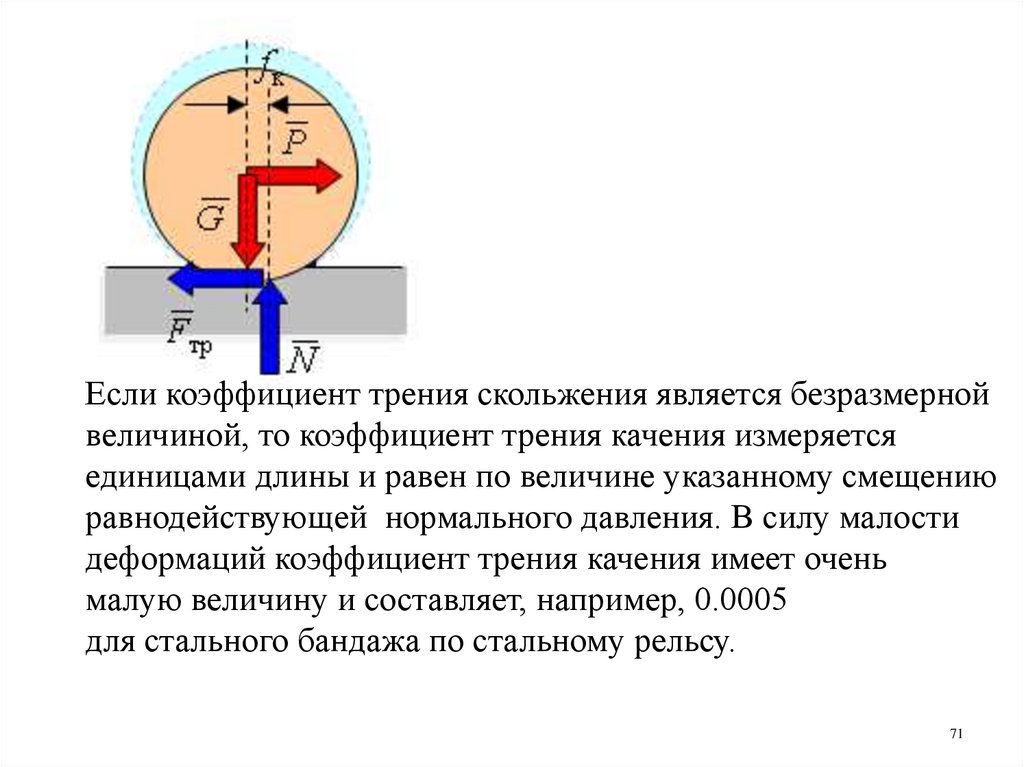
71.
Если коэффициент трения скольжения является безразмернойвеличиной, то коэффициент трения качения измеряется
единицами длины и равен по величине указанному смещению
равнодействующей нормального давления. В силу малости
деформаций коэффициент трения качения имеет очень
малую величину и составляет, например, 0.0005
для стального бандажа по стальному рельсу.
71
72.
Трение принимает участие там, где мы о нем даже и неподозреваем
Когда шьем
Когда завязываем пояс
Когда ходим
Без трения все
нитки выскользали
бы из ткани
Без трения все узлы
бы развязались
Без трения нельзя бы
было ступить и шагу,
да и ,вообще, стоять.
72
73.
Когда едемКогда что-либо ставим или
берем в руки
Без трения колеса бы
просто прокручивались
Без трения все бы
соскальзывало со стола и
выскальзывало из рук
73
74.
Трение в жизни растенийЛианы
Вьюны
Хмель
Благодаря трению цепляются за находящиеся поблизости опоры,
Удерживаются на них и тянутся к свету
74
75.
Репейнику трение помогает распространятьсемена, имеющие колючки.
Семена гороха, орехи благодаря шарообразной
форме и малому трению качения перемещаются
легко сами.
75
76.
Трение в жизни животныхЧтобы увеличить сцепление с грунтом, стволами деревьев, на конечностях
животных имеется целый ряд различных приспособлений: когти, тело
пресмыкающихся покрыто бугорками и чешуйками
76
77.
Fтр скольжения зависит от угла наклонаУгол
наклона
10
20
30
45
Fтр
Скольжения
1H
1,5H
1,8H
2,3H
77
78.
ЭкспериментЗависимость Fтр скольжения от нагрузки
m, гр
160
260
360
F;H
0,5
0,8
1
78
79.
Страница историиЛеонардо да
Винчи
Кулон Шарль
Огюстен де
Эйлер
Леонард
Петров Василий
Владимирович
15.04.1452-02.05.1519
14.06.1736-23.08.1806
15.04.1707-18.09.1783
19.07.1761-03.08.1834
79
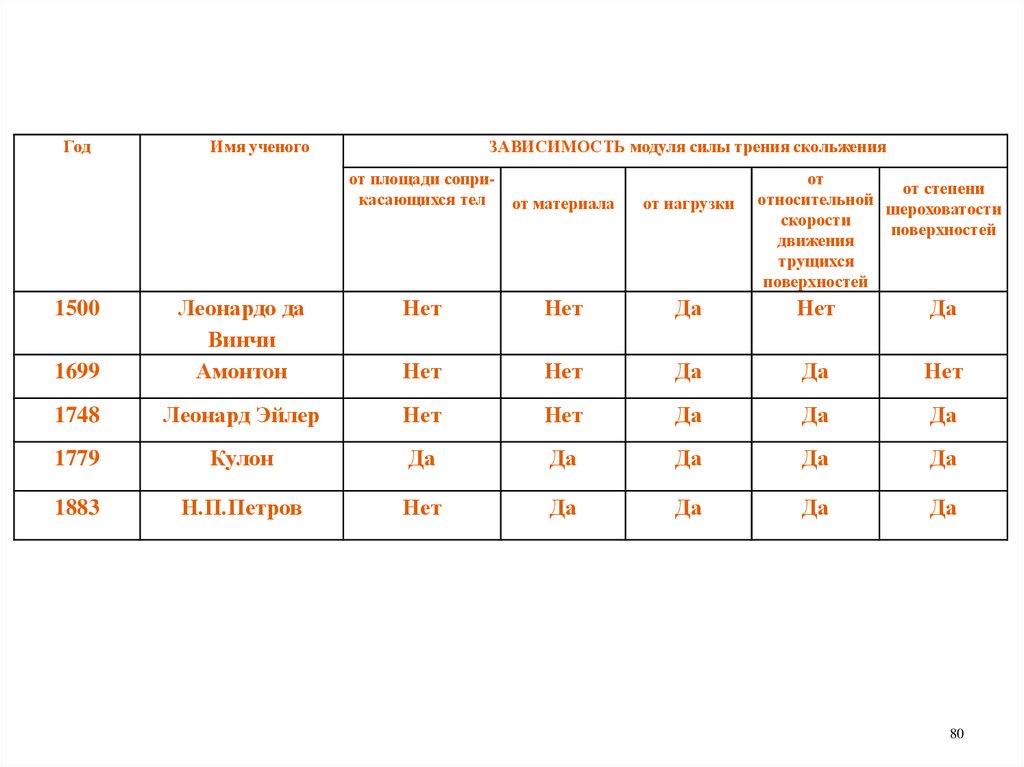
80.
ГодИмя ученого
ЗАВИСИМОСТЬ модуля силы трения скольжения
от площади соприкасающихся тел
от материала
от нагрузки
от
от степени
относительной
шероховатости
скорости
поверхностей
движения
трущихся
поверхностей
Нет
Нет
Да
Нет
Да
1699
Леонардо да
Винчи
Амонтон
Нет
Нет
Да
Да
Нет
1748
Леонард Эйлер
Нет
Нет
Да
Да
Да
1779
Кулон
Да
Да
Да
Да
Да
1883
Н.П.Петров
Нет
Да
Да
Да
Да
1500
80
81.
И думал он:Отсель грозить мы будем шведу,
Здесь будет город заложен
На зло надменному соседу.
Природой здесь нам суждено
В Европу прорубить окно,
Ногою твердой стать при море.
Сюда по новым им волнам
Все флаги в гости будут к нам
И запируем на просторе.
81
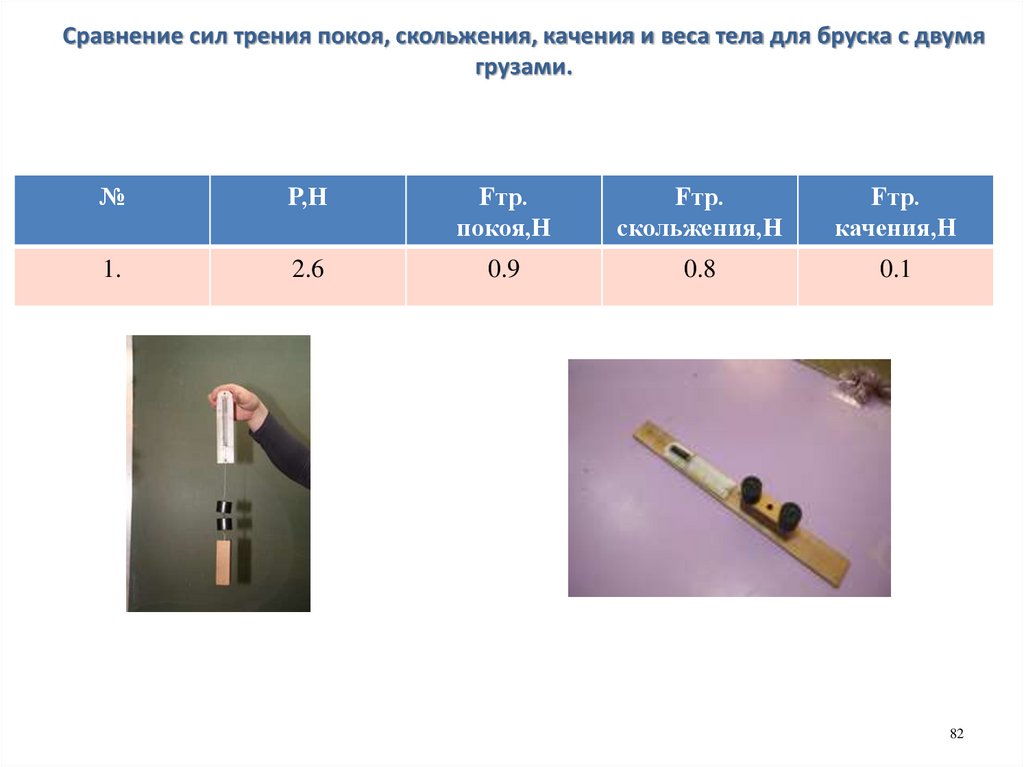
82.
Сравнение сил трения покоя, скольжения, качения и веса тела для бруска с двумягрузами.
№
P,Н
Fтр.
покоя,Н
Fтр.
скольжения,Н
Fтр.
качения,Н
1.
2.6
0.9
0.8
0.1
82
83.
Зависимость силы трения от площади соприкосновения трущихсяповерхностей.
S (см2)
20
28
FTp(H)
0,35
0,35
83
84.
Зависимость силы трения от вида трущихсяповерхностей.
Вид поверхностей
Fтр;Н
Дерево по дереву
0.8
Дерево по картону
0.9
Дерево по резиновому коврику
1.5
Дерево по наждачной бумаге
1.8
Дерево по стеклу
0.7
84
85.
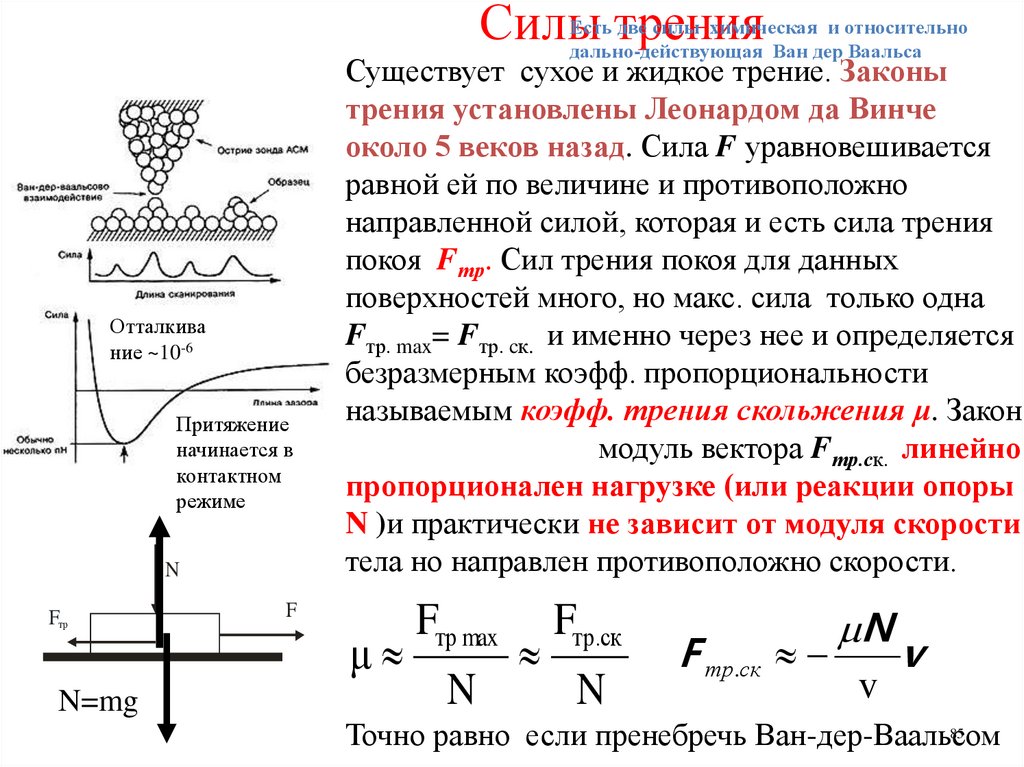
Силы тренияЕсть две силы химическая и относительно
дально-действующая Ван дер Ваальса
Отталкива
ние ~10-6
Притяжение
начинается в
контактном
режиме
N
Fтр
N=mg Рис. 13
Существует сухое и жидкое трение. Законы
трения установлены Леонардом да Винче
около 5 веков назад. Сила F уравновешивается
равной ей по величине и противоположно
направленной силой, которая и есть сила трения
покоя Fтр. Сил трения покоя для данных
поверхностей много, но макс. сила только одна
Fтр. max= Fтр. cк. и именно через нее и определяется
безразмерным коэфф. пропорциональности
называемым коэфф. трения скольжения μ. Закон
Amontons' (1699 ): модуль вектора Fтр.ск. линейно
пропорционален нагрузке (или реакции опоры
N )и практически не зависит от модуля скорости
тела но направлен противоположно скорости.
F
μ
Fтр max
N
Fтр.ск
N
F тр.ск
N
v
v
85
Точно равно если пренебречь Ван-дер-Ваальсом
86.
Сила трения сухого тренияN
Если горизонтальная поверхность т.е. =0 ? проекция mg
Fтр
на горизонтальную ось x равна 0 и при начале скольжения
max= F-Fтр=F–μmg=0 или для баланса сил и обеспечения
хотя бы нулевого ускорения (не нулевой начальной
скорости) a=(F/m- μ g) =0 или F/m=μg или F= μmg. Сила
N=mgРис. 13
F линейна пропорциональна массе тела. Сила с
x
которой надо тянуть на санях одного и двух студентов
отличаются в два раза. А для троих надо тройку
запрягать!
Но из опыта: сила трения не зависит от площади соприкосновения. Посмотрим на
F
трибометр. Почему? Fтр определяется химией поверхностей и силой которая их
сдавливает. Чем меньше площадь при той же величине силы сдавливания, тем больше
давление на 1 мм кв. и больше атомов входят в химическое взаимодействие. Трибометр
с двумя брусками. Сила возрасла в 2 раза! Противоречие? Т.е. для начала движения
надо чтобы mgsin - μmgcos =mg(sin - μcos )=0 или μ =tg ! Т.е. угол наклона доски в
момент сползания бруска определяется только величиной μ, а не m. А почему нет
зависимости от скорости? Так как короткодейтвие (химия) . Сила действует только
на маленьком расстоянии. Т.е. факт химическая молекула создана! При малых
скоростях с какой скоростью она создавалась не важно. Важно, что в один и тот же
момент времени есть определенное количество молекул состоящих в химической
связи. Химия в десять раз сильнее Ван-дер-Ваальсовых сил.
86
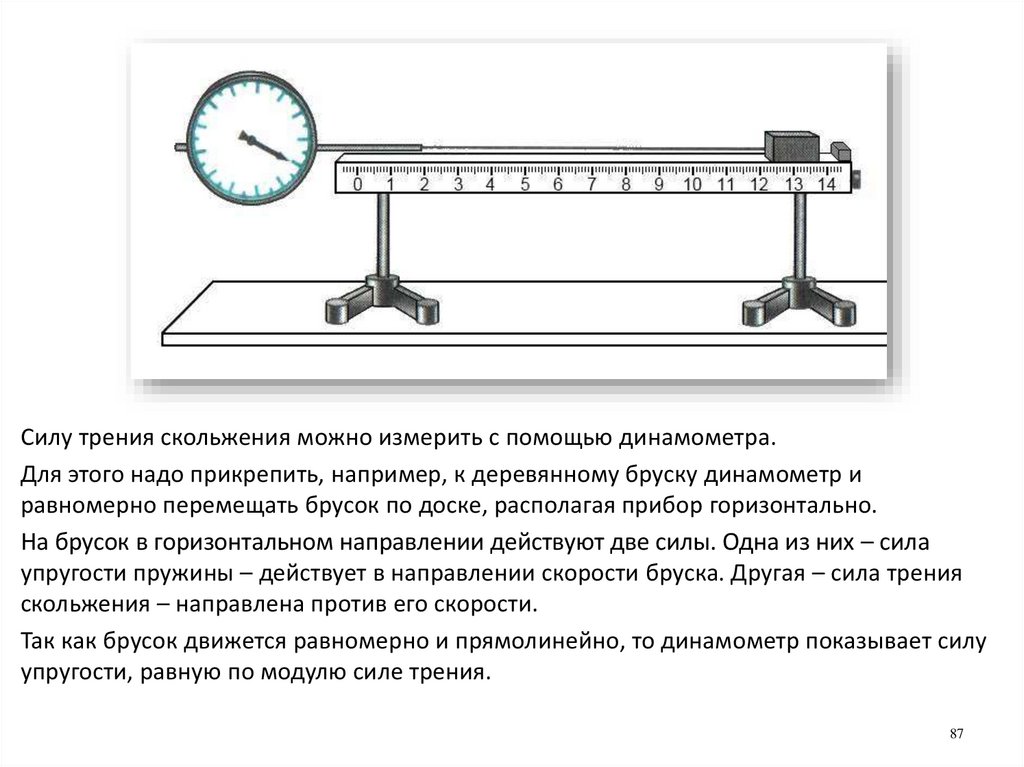
87.
Силу трения скольжения можно измерить с помощью динамометра.Для этого надо прикрепить, например, к деревянному бруску динамометр и
равномерно перемещать брусок по доске, располагая прибор горизонтально.
На брусок в горизонтальном направлении действуют две силы. Одна из них – сила
упругости пружины – действует в направлении скорости бруска. Другая – сила трения
скольжения – направлена против его скорости.
Так как брусок движется равномерно и прямолинейно, то динамометр показывает силу
упругости, равную по модулю силе трения.
87
88.
Если на брусок положить груз и снова перемещать его равномерно поповерхности доски, то показания динамометра изменятся.
Поместим на брусок ещё один груз, чтобы сильнее прижать брусок к доске.
Тем самым мы увеличиваем силу, действующую перпендикулярно поверхности
соприкосновения бруска с грузами и доски.
Эту силу называют силой нормального давления
88
89.
Если снова измерить силу трения, тоокажется, что она увеличилась.
Опыты показывают: чем больше сила
нормального давления, тем больше
возникающая при этом сила трения
скольжения.
Она увеличивается во столько раз, во
сколько увеличивается сила
нормального давления.
По третьему закону Ньютона
модуль силы нормального
давления равен модулю силы
реакции опоры N.
Тогда можно записать: F = μN,
где (греческая буква, читается «мю») – коэффициент
пропорциональности, называемый коэффициентом трения.
Он характеризует не тело, на которое действует сила трения, а
сразу два тела, трущиеся друг о друга.
Графиком зависимости модуля силы трения от модуля силы
89
реакции опоры является прямая линия: сила трения скольжения
90.
1. Введение смазки между трущимися поверхностямиТрение между соприкасающимися
твёрдыми телами (без смазки) называют
сухим трением (рис. а)
Смазка существенно уменьшает силу
трения.
Когда тело движется, соприкасаясь с
жидкой смазкой, то возникает жидкое
трение.
Его часто называют вязким трением (рис.
б).
Коэффициент трения при вязком трении
много меньше коэффициента трения при
сухом трении.
90
91.
2. Использование шариковых и роликовых подшипниковДля уменьшения трения вращающихся валов машин и станков используют подшипники,
заменяющие трение скольжения трением качения. (шариковые и роликовые
подшипники).
Внутреннее кольцо подшипника, изготовленное из твёрдой стали,
насажено на вал. Наружное кольцо подшипника закреплено в
корпусе машины. При вращении вала внутреннее кольцо начинает
не скользить, а катиться на шариках или роликах, находящихся
между кольцами. Опыт показывает, что силы трения качения
значительно меньше сил трения скольжения ( износ
вращающихся частей машин значительно медленнее).
91




























































 Физика
Физика








