Похожие презентации:
Операции над событиями
1. Операции над событиями
2.
3.
Какие из следующих событий –случайные достоверные невозможные
после четверга будет пятница;
черепаха научится говорить;
ваш день рождения – 19 октября;
день рождения вашего
друга – 30 февраля;
вы выиграете, участвуя в лотерее;
вы не выиграете, участвуя
в беспроигрышной лотерее;
вы проиграете партию в шахматы;
на следующей неделе испортится погода;
после пятницы будет четверг;
вы нажали на звонок, он не зазвонил;
4.
Классическое определениевероятности
1)В урне 15 белых и 25 чёрных
2)Из русского алфавита
шаров. Из урны наугад
вынимается один шар. Какова
вероятность того, что он будет
белым?
случайным образом выбирается
одна буква. Какова вероятность
того, что она окажется гласной?
3) Из слова СОБЫТИЕ случайным
образом выбирается одна буква.
Какова вероятность того, что она
окажется гласной?
4) Абонент забыл последнюю цифру
телефонного номера и набрал её на
удачу, помня только, что эта цифра
нечётная. Найти вероятность того,
что номер набран правильно.
5) Одновременно бросают 3 монеты. 6) Одновременно бросают 3 монеты.
Сколько равновозможных исходов у С какой вероятностью все монеты
этого эксперимента?
выпадут на одну сторону?
5.
6.
7.
8. Операции над множествами
А = {4, 5, 6, 7}, B = {6, 7, 8, 9, 10, 11}Объединение множеств:
A B 4, 5, 6, 7, 8, 9, 10, 11
Пересечение множеств:
A B 6, 7
9.
10. Противоположное событие и его вероятность
Ā – событие, противоположное АĀ
A
Событие А: выпадет число меньше трех
1
Множество исходов А = {1, 2};
Р(А) =
3
Событие Ā: выпадет число больше или равное трем
2
Множество исходов Ā= {3, 4, 5, 6}; Р(Ā) =
3
Событие Е: выпадет пятерка
1
Множество исходов Е = {5}; Р(Е) =
6
Событие Ē = выпадет не пятерка
5
Множество исходов Ē = {1, 2, 3, 4, 6}; Р(Ē) =
6
Р(Ā) = 1 – Р(А)
11. Объединение и пересечение событий
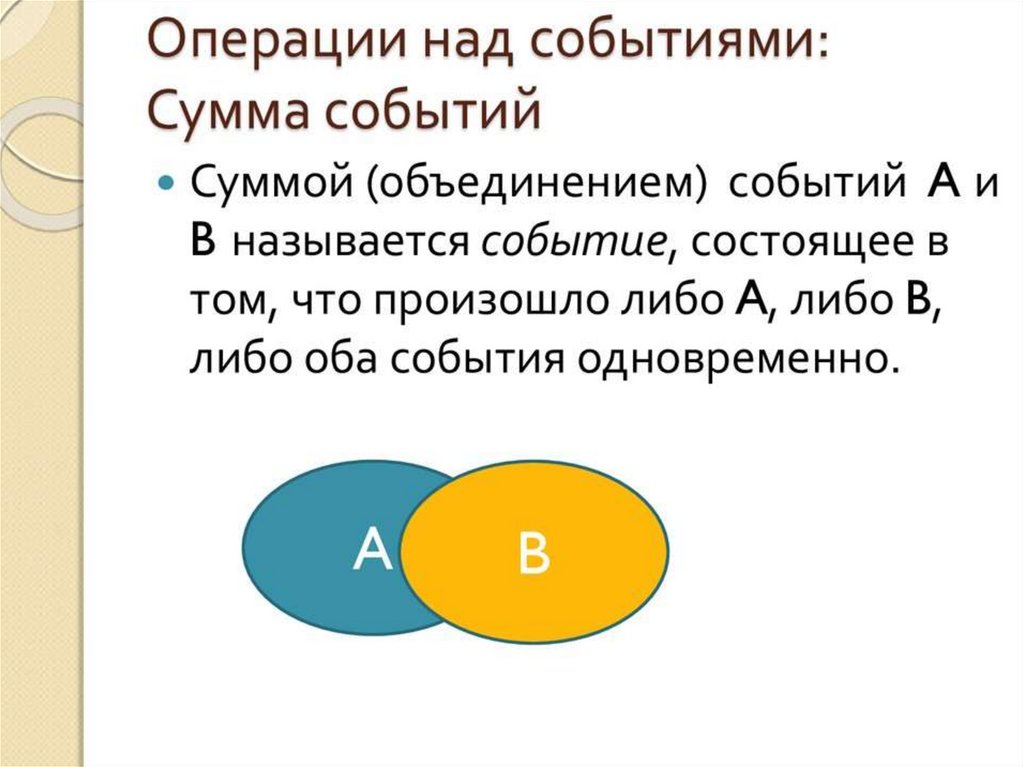
Объединением событий А и В называется событие С,которое происходит тогда и только тогда, когда
происходит хотя бы одно из двух событий А или В
C A B
Пересечением событий А и В называется событие С,
которое происходит тогда и только тогда, когда
происходят одновременно оба события А и В
C A B
12. Несовместные события
Два события А и В называются несовместными, если ихпресечение пусто
Событие А: выпала тройка
Событие В: выпала пятерка
A B
1
Р(А) =
6
1
Р(В) = 6
Событие С: выпала тройка или пятерка (С = А U В)
1 1 1
Р(С) = Р(А U В) = Р(А) + Р(В) =
6 6 3
13. Формула сложения вероятностей для несовместных событий
Р(А U В) = Р(А) + Р(В)В урне 3 красных и 5 желтых шаров. Какова
вероятность того, что будут выбраны два шара
одного цвета?
Р(А1UА2U…UAk) = Р(А1) + Р(A2)+…+P(Ak)
14. Формула сложения вероятностей для произвольных событий
Если события А и В пересекаются, т.е. совместны, товероятность их объединения можно найти по формуле
Р(А U В) = Р(А) + Р(В) – Р(А В)
Бросают два кубика. С какой вероятностью
будет выброшена хотя бы одна шестерка?
Событие А: шестерка выпала на первом кубике
Событие В: шестерка выпала на втором кубике
Событие А U В: шестерка выпала хотя бы на одном кубике
Событие A B : выпали две шестерки
1 1 1 11
Р(А U В) =
6 6 36 36
15.
16. Независимые события
Два события А и В называются независимыми,если выполняется равенство
Р(А В) = Р(А) Р(В)
Из первых n натуральных чисел наугад
выбирается число.
Событие А: выбранное число – четное.
Событие В: выбранное число кратно трем.
Выяснить, являются ли события А и В
независимыми, если : 1) n = 10; 2) n = 20;
3) n = 30.
17. Независимые события
Выясните, являются ли события А и Внезависимыми.
1) В одной урне находятся 5 белых и 7 красных
шаров, а в другой – 6 белых и 6 красных шаров.
Событие А: из 1-ой урны вынут белый шар
Событие В: из 2-ой урны вынут белый шар
2) В урне находятся 5 белых и 7 красных шаров
Событие А: первым вынут вынут белый шар
Событие В: вторым вынут красный шар
18. Условные вероятности
Đ( A B) P( A) P( A | B)В урне находятся 5 белых и 7 красных шаров
Событие А: первым вынут вынут белый шар
Событие В: вторым вынут красный шар
Р(А) = 5/12,
Р(В|А) = 7/11
5 7
35
P( A B)
12 11 132


















 Математика
Математика








