Похожие презентации:
Сечение многогранника плоскостью
1. Сечение многогранника плоскостью
Рабочая тетрадьстраница 34
2.
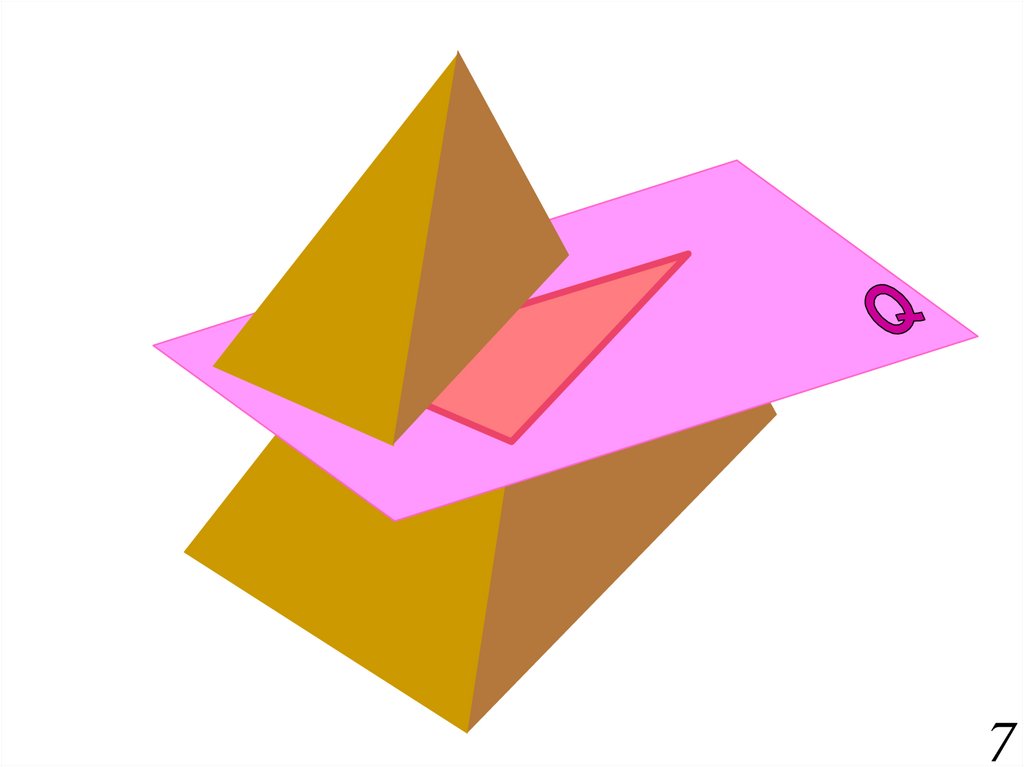
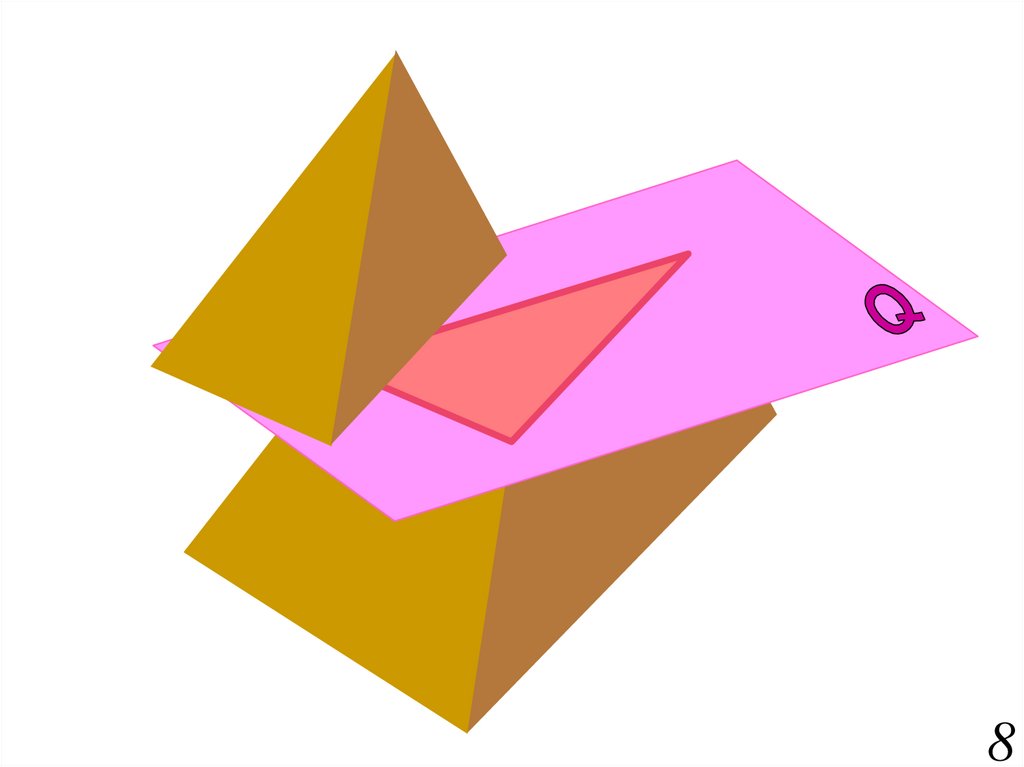
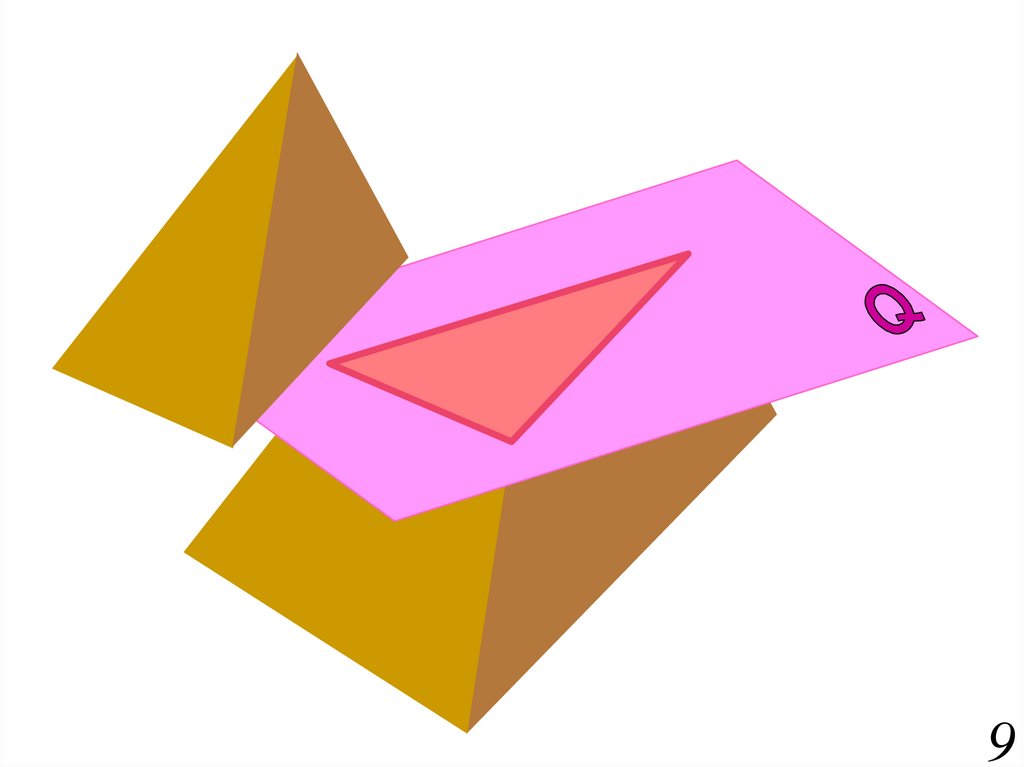
В пересечении гранных поверхностей
плоскостями
получаются
многоугольники.
Их
вершины
определяются как точки пересечения
ребер гранных поверхностей с секущей
плоскостью.
2
3.
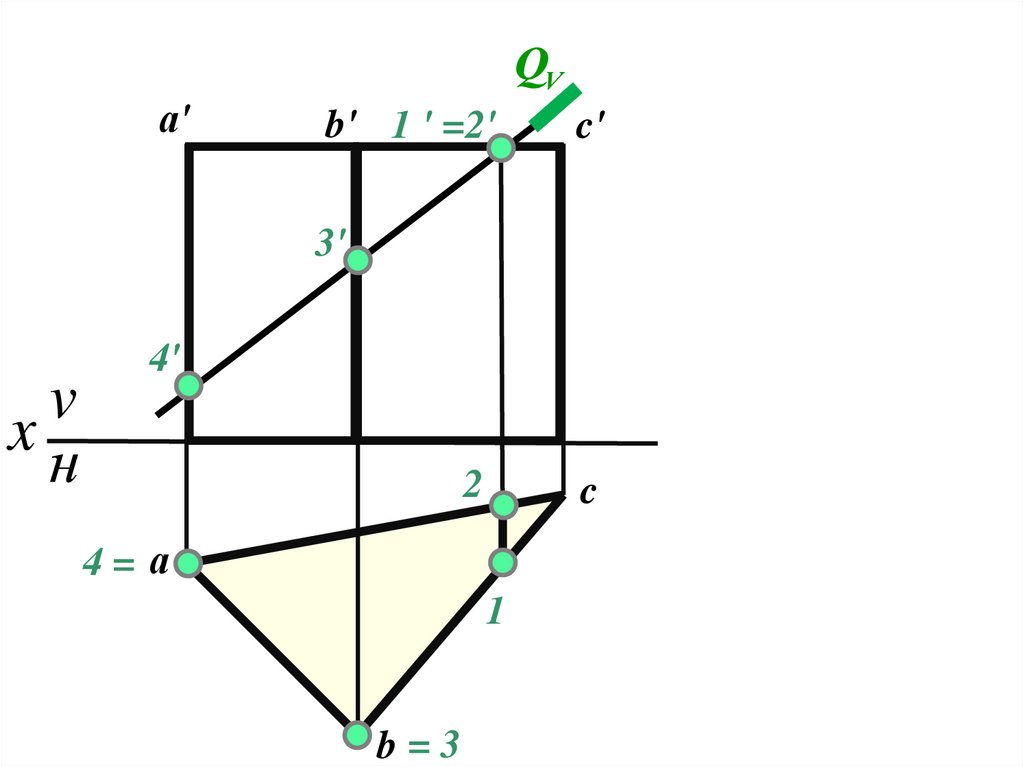
Призма4.
а'QV
b' 1 ' =2'
c'
3'
v
x
н
4'
2
c
4= а
1
b=3
5.
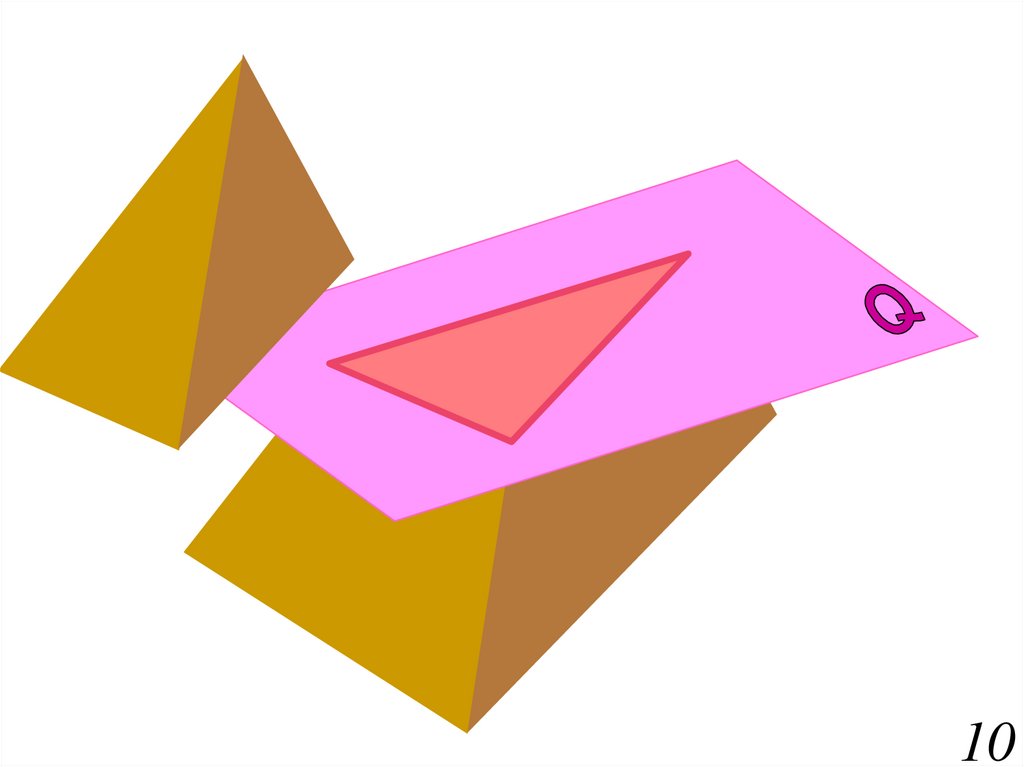
Пирамида6.
67.
78.
89.
910.
1011.
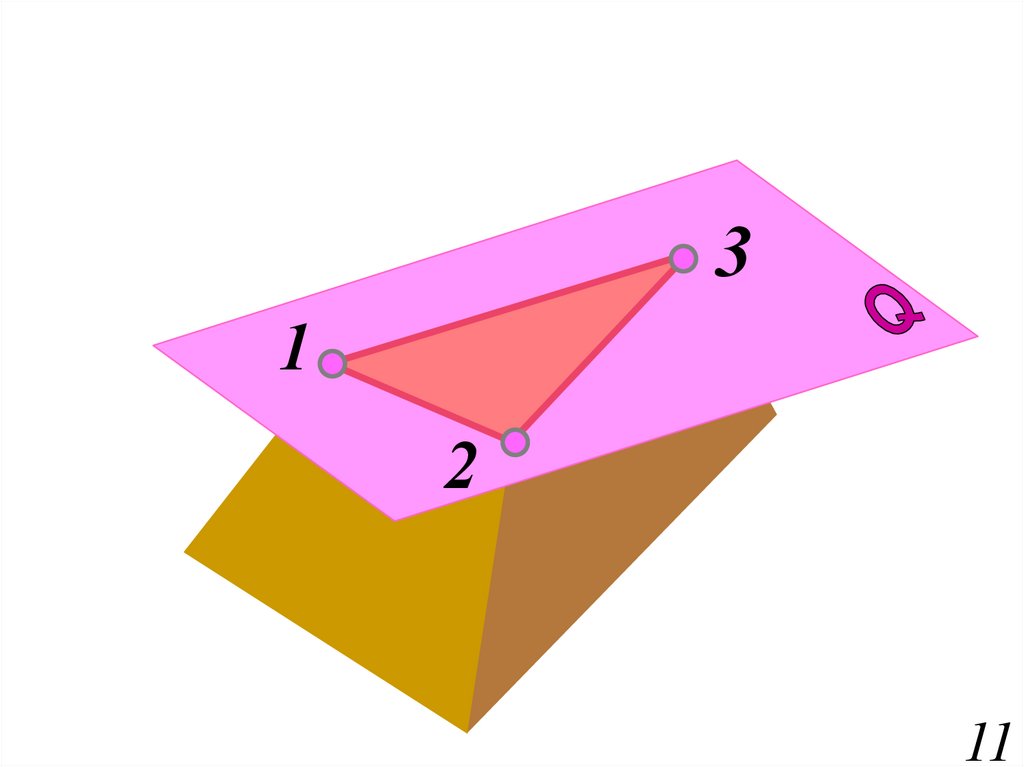
31
2
11
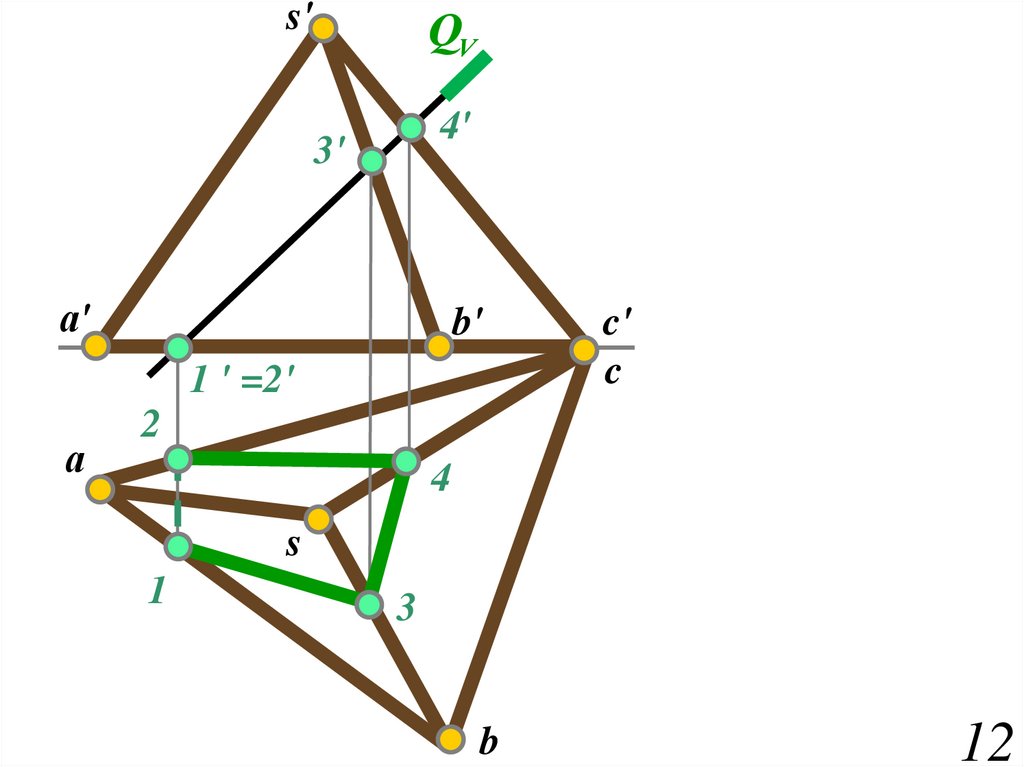
12.
s'QV
4'
3'
а'
b'
1 ' =2'
а
c'
c
2
4
s
1
3
b
12
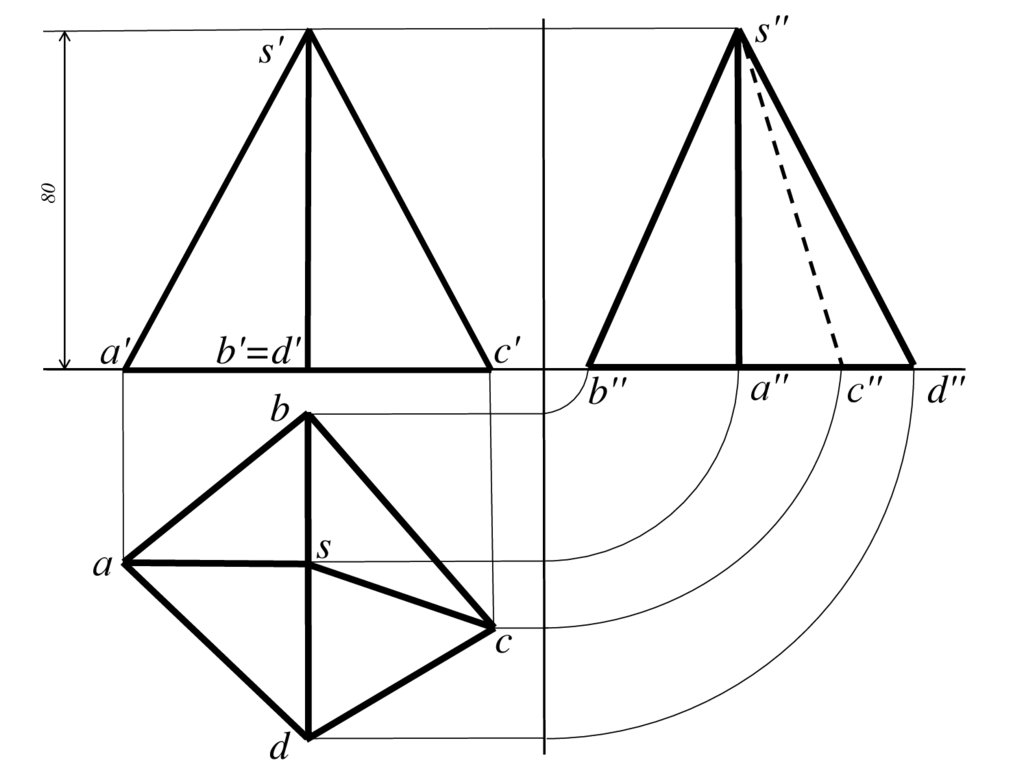
13. Построение третьей проекции пирамиды (либо на последнем форзаце тетради, либо на листе в клетку)
1314.
s''80
s'
а'
c'
b'=d'
b
b''
s
а
c
d
а''
с''
d''
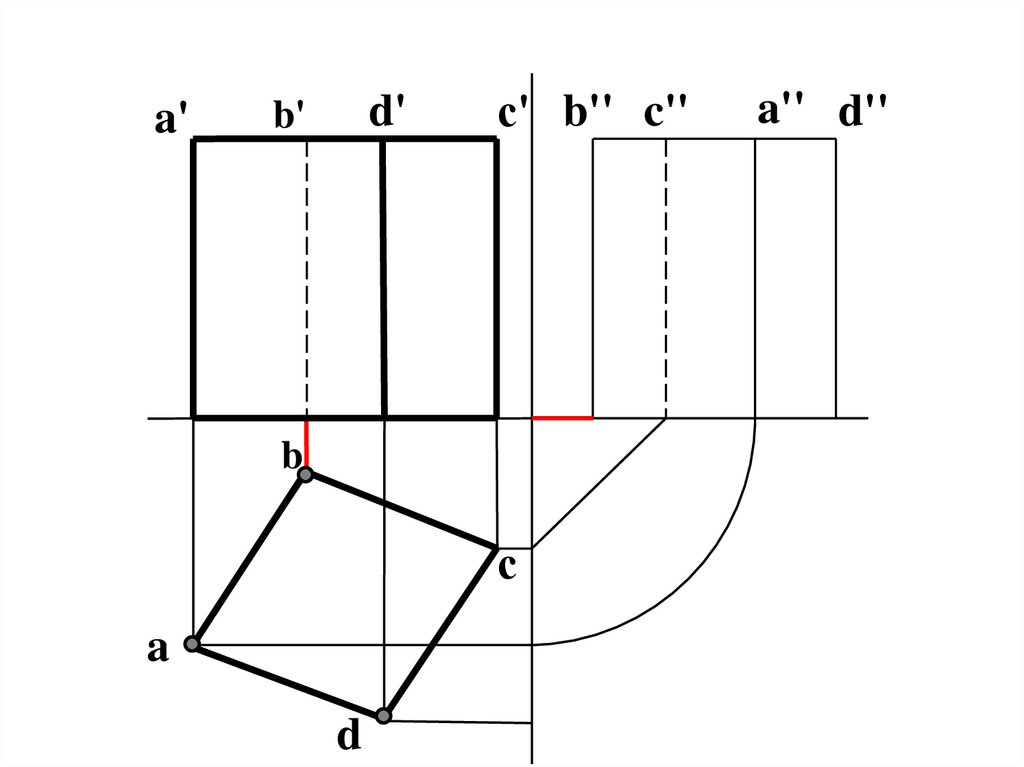
15. Построение третьей проекции призмы
1516.
a'd'
b'
с' b'' c''
b
с
a
d
a'' d''
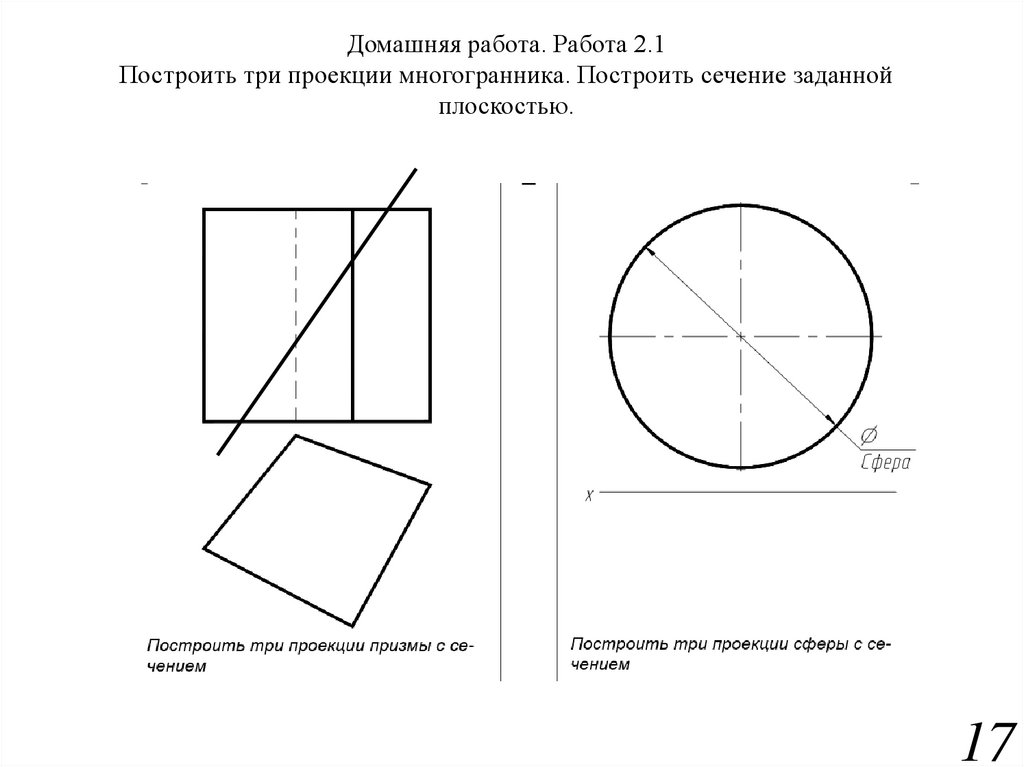
17.
Домашняя работа. Работа 2.1Построить три проекции многогранника. Построить сечение заданной
плоскостью.
17
18. Сечение многогранника плоскостью
Рабочая тетрадьстраница 34







 Математика
Математика Инженерная графика
Инженерная графика








