Похожие презентации:
Вычислительная математика. Численное дифференцирование
1.
№3ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
ЧИСЛЕННОЕ
ДИФФЕРЕНЦИРОВАНИЕ
2.
№3ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
К численному (приближенному)
дифференцированию чаще всего
прибегают, когда приходится вычислять
производные от функций, заданных
таблично, или, когда непосредственное
дифференцирование затруднено.
3. ……
.4.
..5.
..6.
..7.
..8.
..9.
..10.
№3ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Пример
f ( x) x
Вычислить производную функции
в точке x 2 с точностью 0,005.
2
Решение
x 0,1.
Задаем начальное приращение
f ( x ) f ( x) 2.12 22
Вычисляем f 1:
4.1;
0.1
Изменяем приращение
x 0.1/10 0.01.
2.012 22 4.0401 4
Вычисляем f 2 :
4.01;
0.01
0.01
11.
№3ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Проверяем условие окончания вычислений:
f 1 f 2 0.005 :
4.1 4.01 0.09 0.005.
f 1: 4.01.
Точность не достигнута, поэтому
Изменяем приращение x 0.01/10 0.001.
2
2
2.001
2
4.0401 4
Вычисляем f 2 :
4.001;
0.01
0.01
Погрешность не достигнута
4.01 4.001 0.009;
f 1: 4.001; x 0.001/10 0.0001.
2.00012 22
f 2 :
4.0001; 4.001 4.0001 0.0009;
0.01
0.0009 0.005,
f ( x) 4.0001
12.
№3ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Формула вычисления производной второго
порядка:
2
d f
f ( x) 2
dx
f ( x x) 2 f ( x) f ( x x)
2
( x)
13.
№3ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Формулы численного дифференцирования
функции многих переменных
В этом случае все аргументы функции
становятся константами, кроме аргумента, п
которому проводится дифференцирование.
Пусть дана функцияf ( x1 , x2 ,..., xn ) , тогда
производная xi вычисляется по формуле:
по
f ( x1 ,...xn ) f ( x1 ,..., xi xi ,...xn ) f ( x1,...xi ,...xn )
xi
xi
14.
№3ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Или, используя центральную разность
f ( x1 ,...xn )
xi
f ( x1 ,...xi xi ...xn ) f ( x1 ,...xi xi ...xn )
2 xi
15.
№3ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Вычисление частной производной
второго порядка
На практике используют также формулы
вычисления частных производных высоких
порядков. Ниже приведены формулы для
случая функции двух переменных
f ( x, y)
f ( x, y ) f ( x x, y ) 2 f ( x, y ) f ( x x, y )
2
x
( x) 2
2
f ( x, y ) f ( x, y y ) 2 f ( x, y ) f ( x, y y )
2
y
( y ) 2
2
16.
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА№3
f ( x, y )
[ f ( x x, y y ) f ( x x, y y )
x y
1
f ( x x, y y ) f ( x x, y y )]
4 x y
2
17.
№3ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Конечно-разностные аппроксимации
производных
Пусть отрезок[a, b] разбит наn ( 2) частей
точками{xi }:
x0 x1 x2 ... xi 1 xi xi 1 ... xn .
Далее, пусть на этом отрезке определена
функция yi f ( xi ) (i 0,1, 2,..., n) . Тогда
выражения для первой производной функции
в точкеx i с помощью отношения конечных
разностей запишем следующим образом:
18.
№3ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
а) аппроксимация с помощью разностей впер
(правых разностей)
y i 1 y i
y ( xi )
xi 1 xi
(i 0, 1,..., n 1);
y i y i 1
y ( xi )
xi xi 1
(i 1,2,..., n);
y i 1 y i 1
y ( xi )
xi 1 xi 1
(i 1,..., n 1).
б) аппроксимация с помощью разностей наза
(левых разностей)
в) аппроксимация с помощью центральных
разностей
19.
№3ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Приближенное значение производной второго
порядка в точкеxi :
yi 1 2 yi yi 1
y ( xi )
( xi 1 xi 1 )2
(i 1, 2,...,
n 1).
2
0
(
h
Погрешность аппроксимации имеет порядок ) .
Естественно, что представление с помощью
конечных разностей позволяет вычислять
значения
второй
производной
внутренних точках отрезка.
только
во
20.
№3ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Численные методы
интегрирования
21.
№3ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
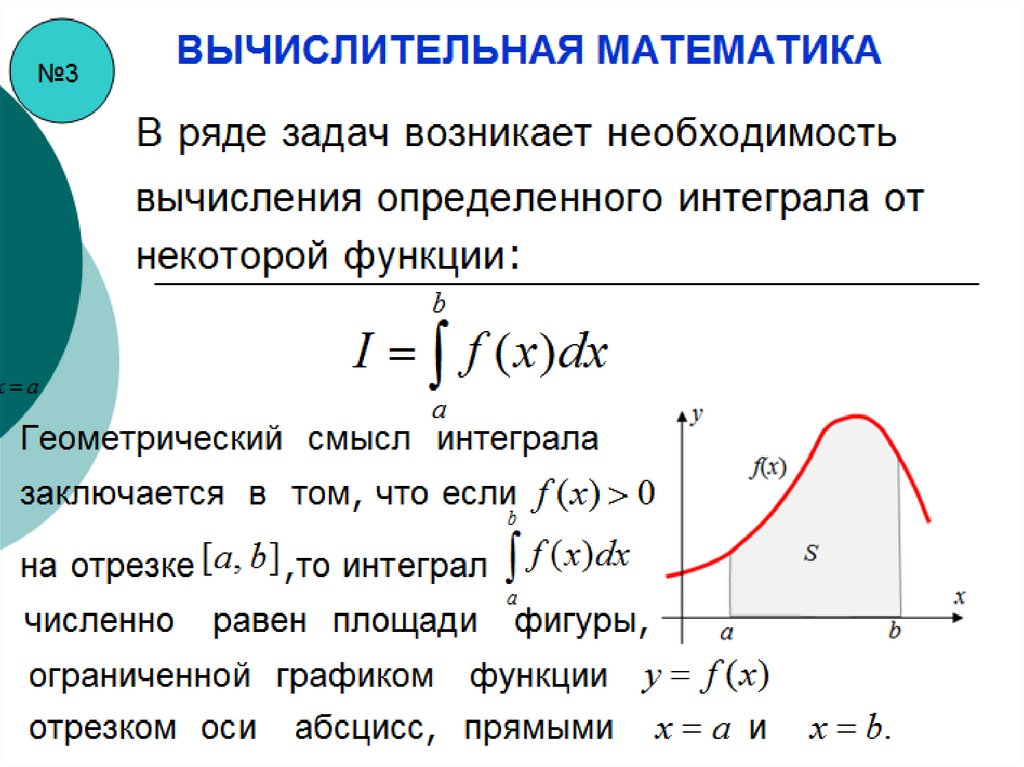
В ряде задач возникает необходимость
вычисления определенного интеграла от
некоторой функции:
b
x a
I f ( x ) dx
a
Геометрический смысл интеграла
заключается в том, что если
f ( x) 0
b
на отрезке[a, b] ,то интеграл f ( x )dx
численно
a
равен площади
фигуры,
y f (x)
ограниченной графиком функции
отрезком оси абсцисс,прямыми x a и
x b.
22.
№3ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Численное интегрирование применяется, ког
•сама подынтегральная функция не задан
аналитически, а например, представлен
в виде таблицы значений;
•аналитическая запись подынтегральной
функции известна, но ее первообразная
не выражается через
аналитические
функции.
23.
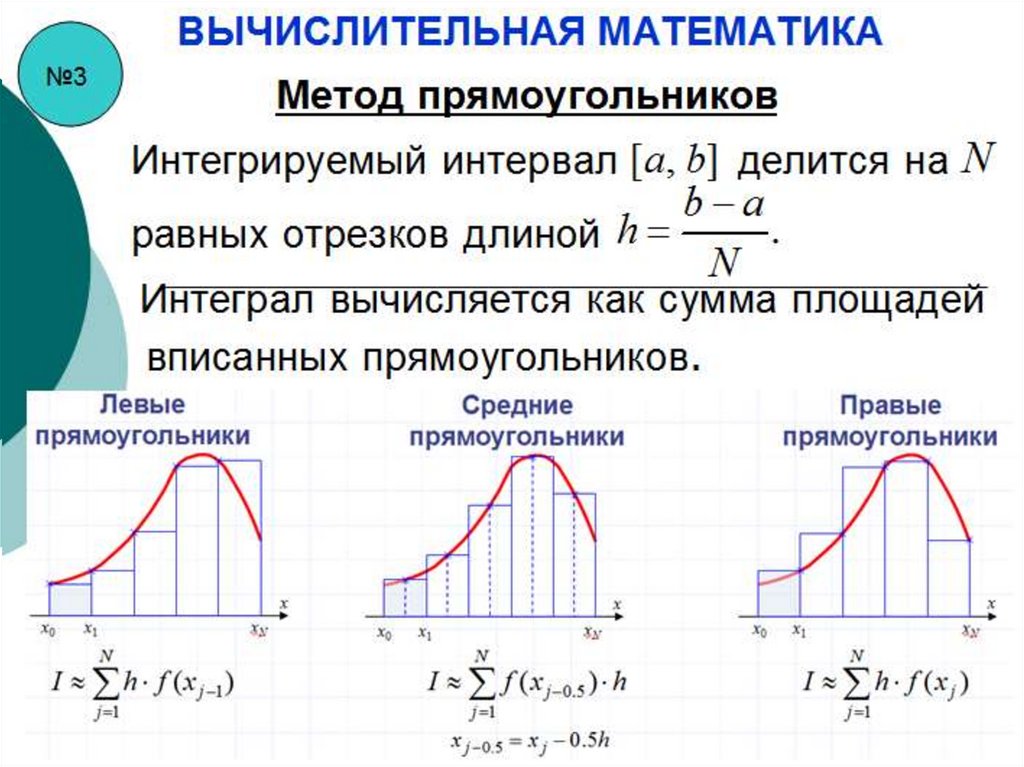
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА№3
Метод прямоугольников
[a, b] делится
Интегрируемый интервал
b на
a
h
.
равных отрезков длиной
N
N
Интеграл вычисляется как сумма площаде
вписанных прямоугольников.
24.
№3ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Метод трапеций
Площадь криволинейной трапеции заменяетс
площадью многоугольника, составленного и
N трапеци
b
й.
N
f ( x)dx
a
f x j f x j 1
j 0
2
b
N
f ( x j 1 ) f ( x j )
a
j 1
2
f ( x)dx h
h
N 1
1
h ( f 0 f N ) f ( xi )
i 1
2
25.
№3ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Метод Симпсона (парабол)
Каждый отрезок аппроксимируется параболо
Парабола проходит через три точки: узлы
интегрированияx j и x j 1 и середину отрезка
x j 0,5 .
[ x j , x j 1 ]
Площадь параболы на отрезке
x j 1
h
x f ( x)dx 6 f j 4 f j 0.5 f j 1
j
26.
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА№3
Тогда интеграл функции на отрезке
[a, b]:
N 1
N 0.5
h
f j 4 f j
a f ( x)dx 6 f0 f N 2
j 1
j 1.5
b
Избавимся от дробных индексов. Разобьем
интервал интегрирования на
N равных
отрезков. Тогда формула Симпсона имеет
вид:
2 N 2
2 N 1
h
f
(
x
)
dx
f
f
2
f
4
f
0
2
N
j
j
a
3
j 2,2
j 1,2
b
27.
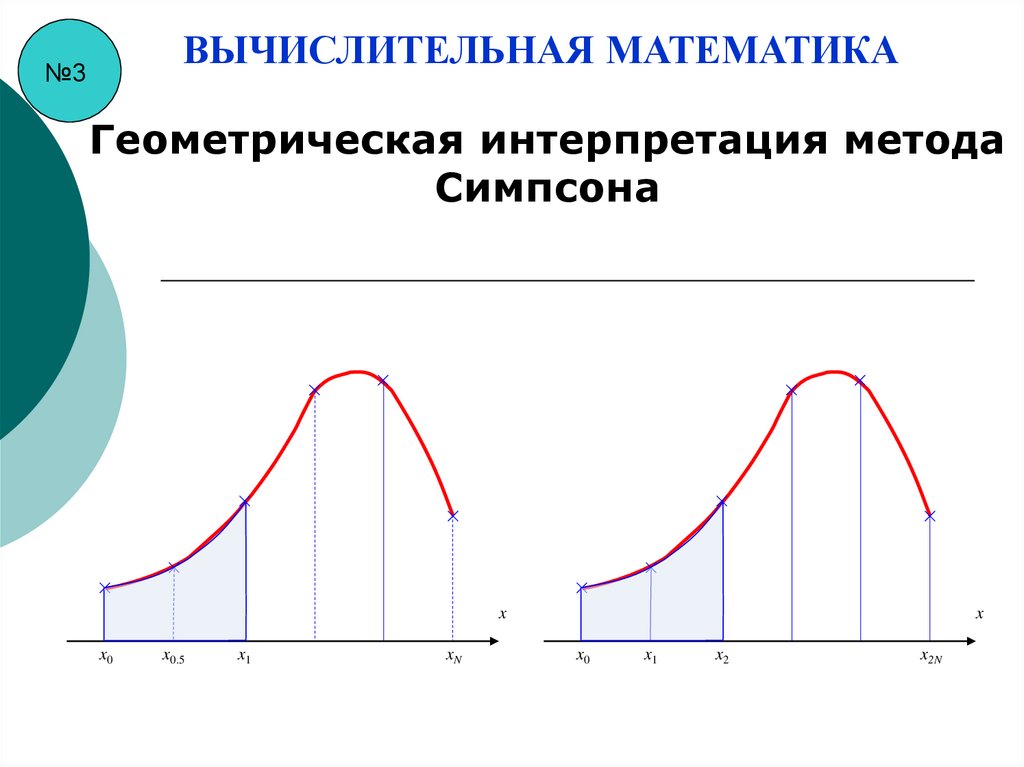
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА№3
Геометрическая интерпретация метода
Симпсона
x
x0
x0.5
x1
xN
x
x0
x1
x2
x2N
28.
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА№3
Метод Уэддля
Метод базируется на применении к каждому
[a, b]формулы:
N отрезков разбиения
3h
f ( x0 5 f ( x1 ) f ( x2 )
x j f ( x ) dx
10
x j 1
6 f ( x3 ) f ( x4 ) 5 f ( x5 ) f ( x6 )).
29.
№3ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Геометрическая интерпретация метода
Уэддля
30.
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА№3
Правило Рунге оценивания погрешности
формул интегрирования
п
Вычисляют величину интегралаI
о
выбранной формуле при числе интервалов
n и 2 n (соответственноI n и I 2n ).
I n I 2n
I n I 2n
3
—для формул правых и левых
прямоугольников;
— для формулы серединных
прямоугольников и трапеций;
31.
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА№3
I n I 2n
15
I n I 2n
— для формулы Симпсона;
— для формулы Уэддля.
63
Если , количество интервалов разбиен
увеличивают вдвое, т.е. значения интегра
вычисляются для последовательных значен
n n, 2n, 4n... Вычисления заканчиваются пр
.
выполнении условия
32.
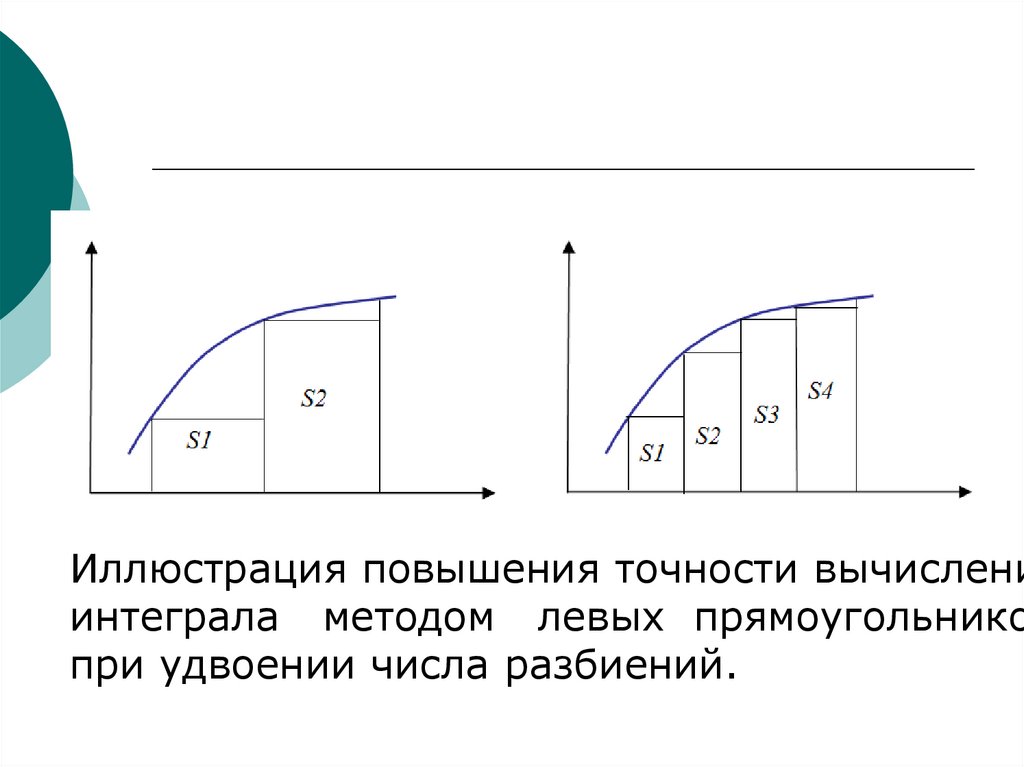
Иллюстрация повышения точности вычислениинтеграла методом левых прямоугольнико
при удвоении числа разбиений.




























 Математика
Математика








