Вычислительная математика. Лекция 4. Аппроксимация функции

1.

4
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Лекция 4
Аппроксимация функции

2.

4
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Задача аппроксимации состоит в том, чтобы по
значениям функции f ( x) в нескольких точках
отрезка восстановить значения в остальных
точках этого отрезка.
Если решаем задачу аппроксимации функции
для всех значений x на отрезке a x b, то
такой способ приближения функции называется
интерполяцией.
Если решаем задачу за пределами отрезка [a, b],
то это задача экстраполяции.

3.

4
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Задача интерполяции
Пусть функция f(x) задана таблицей своих
значений xi, yi: на интервале [a; b]:
yi f xi i 0,1, , n
a xi b
Задача интерполяции - найти функцию
F(x), принимающую в точках xi те же
значения yi
точки xi – узлы интерполяции
условие F(x)= yi – условие интерполяции

4.

4
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
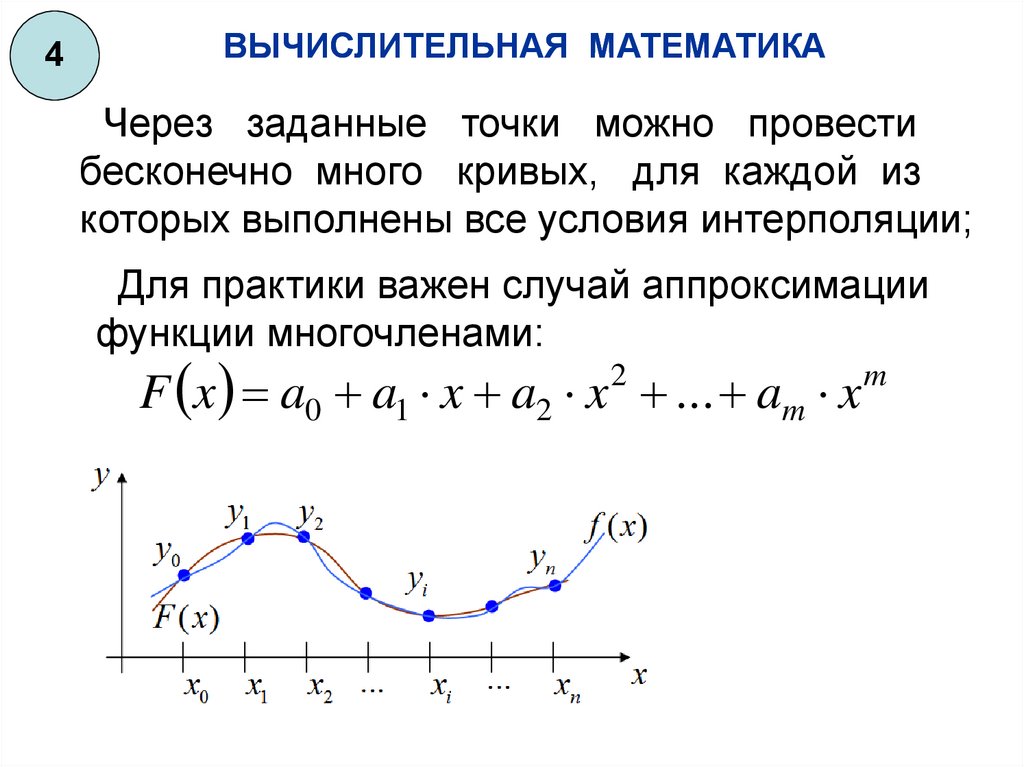
Через заданные точки можно провести
бесконечно много кривых, для каждой из
которых выполнены все условия интерполяции;
Для практики важен случай аппроксимации
функции многочленами:
F x a0 a1 x a2 x ... am x
2
m

5.

4
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Интерполяционный полином Лагранжа
На интервале [ a, b] строится полином степени n :
n
Ln x yi li ( x)
i 0
, где
x xk
x x0 x x1 x xi 1 x xi 1 x xn
li ( x)
xi x0 xi x1 xi xi 1 xi xi 1 xi xn
k 1 xi xk
n
k i
(
x
x
)
j
n
j k
f ( xk ).
Окончательно : Ln ( x)
k 0 ( xk x j )
j k
Полином Лагранжа имеет малую погрешность при
небольших значениях n 20. При больших n
погрешность начинает расти.

6.

4
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Пример.
Для функции, имеющей аналитическое выражение
y x задана интерполяционная таблица:
а) Составить интерполяционный многочлен
второго порядка.
б) Вычислить значение
L2 (115).

7.

ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
4
Решение
а)
n
(x x j )
k 0
( xk x j )
Ln ( x) j k
f ( xk ).
j k
( x 121)( x 144)
( x 100)( x 144)
L2 ( x) 10
11
(100 121)(100 144)
(121 100)(121 144)
( x 100)( x 121)
12
.
(144 100)(144 121)
б)
(115 121)(115 144)
(115 100)(115 144)
L2 (115) 10
11
(100 121)(100 144)
(121 100)(121 144)
115 100 115 121
12
1,88312 9,90683 1,06719 10,7228
144 100 144 121

8.

4
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА

9.

4
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА

10.

4
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА

11.

4
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА

12.

4
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА

13.

4
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА

14.

4
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Интерполяционная формула Ньютона
Pn ( x) f ( x0 ) ( x x0 ) f ( x0 ; x1 ) ( x x0 )( x x1 ) f ( x0 ; x1 ; x2 ) ...
( x x0 )( x x1 )....( x xn 1 ) f ( x0 ; x1 ;...; xn ),
где
f ( x0 ; x1 ),
f ( x0 ; x1 ; x 2 ),
f ( x0 ; x1 ;... x xn )
- разделенные разности, вычисляемые по формулам:
f ( xi 1 ) f ( xi )
f ( xi ; xi 1 )
, i 0, 1, ..., n 1,
xi 1 xi
f ( xi ; xi 1 ; x1 2 )
f ( xi 1 ; xi 2 ) f ( xi ; xi 1 )
, i 0, 1, ..., n 2,
x 2 xi
f ( x1 ; x2 ;... xn ) f ( x0 ; x1 ;...; xn 1 )
f ( x0 ; x1 ;...; xn )
.
xn x0

15.

ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
4
Пример
В таблице приведены данные для f ( x) sin x .
6
Вычислим с помощью полинома Ньютона P4 (0,7).
Решение
Сначала составляем таблицу разделенных
разностей :

16.

4
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Далее вычисляем значения полинома Ньютона, используя
используя подчеркнутые разделенные разности.
Pn (0.7) 0 0.7 0.51764 0.7 0.2 ( 0.0.3528)
0.7 0.2 ( 0.3)( 0.02114) 0.7 0.2 ( 0.3)( 1.3) 0.0192 0.35840
Точное значение sin x 0,35837.
6

17.

4
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Интерполирование в случае
равноотстоящих узлов
В случае равноотстоящих узлов интерполяции
используют первую и вторую интерполяционные
формулы Ньютона.
Конечными разностями функции
называются разности вида:
yi yi 1 yi
y f (x)
— конечные разности первого порядка,
2 yi yi 1 y—
i конечные разности второго порядка,
...............................................................................
k yi k 1 yi 1 k 1 yi — конечные разности k -го порядка.

18.

4
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Пример таблицы конечных разностей для n 5
.

19.

ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
4
Первая интерполяционная формула Ньютона
q (q 1) 2
y ( x) Pn ( x) y0 q y0
y0
2!
q (q 1) (q n 1) n
y0
n!
где
x x0
q
, h xi 1 xi const
h
В формуле используется верхняя горизонтальная строка
таблицы разностей.
Первая формула Ньютона используется для
интерполирования в точках, близких к началу таблицы.

20.

4
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
При n 1 и n 2 получаем частные случаи:
линейная интерполяция
y ( x) y0 q y0
квадратичная интерполяция
q (q 1) 2
y ( x) y0 q y0
y0
2!

21.

4
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
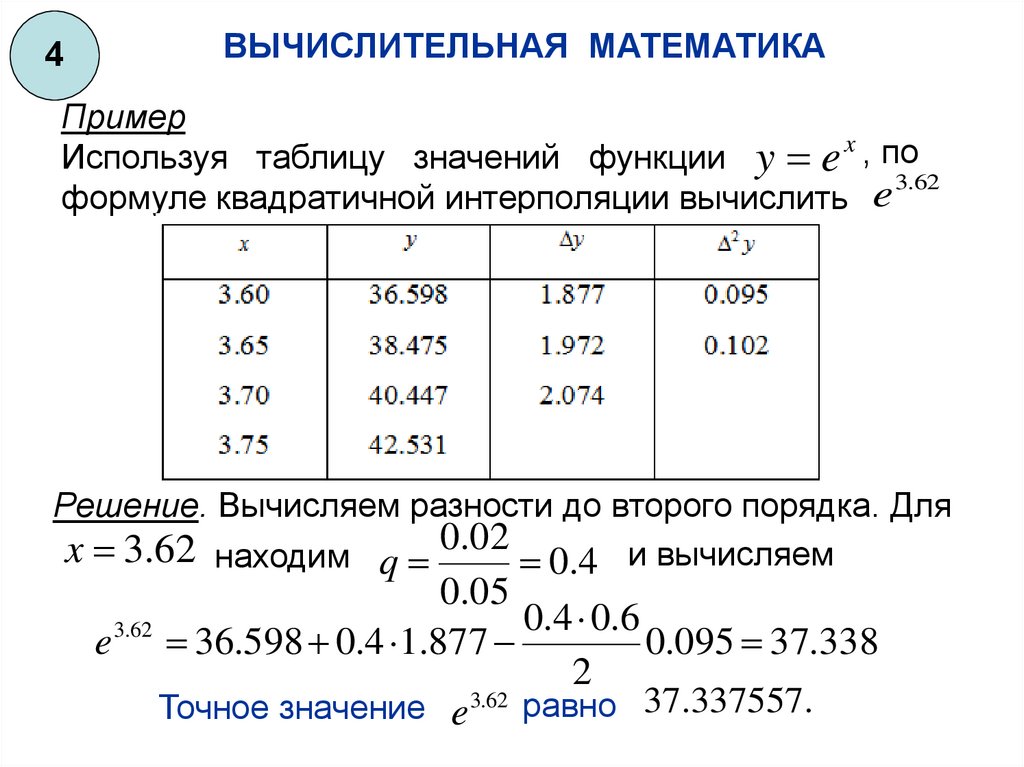
Пример
x
Используя таблицу значений функции y e , по
3.62
формуле квадратичной интерполяции вычислить e
Решение. Вычисляем разности до второго порядка. Для
x 3.62 находим q 0.02 0.4 и вычисляем
0.05
0.4 0.6
3.62
e 36.598 0.4 1.877
0.095 37.338
2
Точное значение e 3.62 равно 37.337557.

22.

4
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Вторая интерполяционная формула Ньютона
q (q 1) 2
y ( x) Pn ( x) yn q yn 1
yn 2
2!
q (q 1) ( q n 1) n
y0
n!
x xn .
где q
h
В формуле используется нижняя наклонная строка
таблицы разностей.
Формула используется для интерполирования в точках,
близких к концу таблицы.

23.

4
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Использование интерполяционных
многочленов для
численного дифференцирования
Продифференцируем
q(q 1) 2
q (q 1)(q 2)...( q n 1) n
Pn ( x) q y 0
y 0 ...
y0
2!
n!
Заметим, что
df ( x) df ( x) dq 1 df ( x)
,
dx
dq dx h dq
x x0
(q
)
h
Будем рассматривать полином 4-го порядка.
P4 ( x)
1
1
3q 2 6q 2 3
2q 3 9q 2 11q 3 4
2
y0 (2q 1) y0
y0
y0 ... .
h
2
6
12

24.

ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
4
На практике для вычисления первой производной
обычно используют полином 3-го порядка, при
этом за начальный узел сетки берут ближайший
слева от точки интерполирования или
дифференцирования. Иными словами, если точка
интерполирования xi x xi 1 то в качестве
y0 , y1 , y2 , y3
берут
y0 yi ,
y1 yi 1 ,
y2 yi 2 ,
y3 yi 3

25.

4
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Дифференцируя
Pn ( x) , получим формулу для
второй производной:
,
1 2
6q 18q 11 4
3
P4 ( x) 2 y0 (q 1) y0
y0 ...
h
12
2
так как
df ( x) df ( x) dq
f ( x)
.
dx
dq dx

26.

ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
4
Пример
Функция
y f (x) задана таблично:
Методом численного дифференцирования найти
y (2.3)

27.

ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
4
Решение. Составим таблицу конечных разностей:
Шаг этой таблицы
Согласно формуле
h 1;
2 .3 1
q
1 .3.
1
2
1
1
3
q
6q 2 3
2
y ( x) y0 (2q 1) y0
y0
h
2
6
имеем:
1
12
6
2
f ( x) 5 (1.3 2 1) (3 1.3 6 1.3 2) 13.87
h
2
6

28.

4
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Формулы приближенного дифференцирования
для определения производных
в узлах интерполяции
2
3
4
5
y0 y0 y0 y0
1
f ( x) y0
...
h
2
3
4
5
1 2
11 4
5 5
3
f ( x) 2 y0 y0 y0 y0 ... .
h
12
6

29.

ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
4
Пример
Функция
y f (x) задана таблично:
Методом численного дифференцирования найти
первые две производные этой функции в точке
x 1.

30.

4
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Решение. Составим таблицу конечных разностей:
Шаг этой таблицы h 1.
Согласно формуле
2 y0 3 y0
1
;
f ( x) y0
h
2
3
1 12 6
f (1) 5 1
h
2 3
Вычислим вторую производную в узле x 1
f ( x)
1 2
3
y
y0 ;
0
2
h
f (1) 6.

31.

4
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
b
Подстановка в интеграл f ( x)dx вместо функции
a
f (x) ее интерполяционного полинома той или
иной степени n приводит к семейству квадратурных
формул, называемых формулами Ньютона-Котеса.
Для того, чтобы использовать полином Ньютона
вместо f (x) , нужно изменить границы
интегрирования (значению x a соответствует
значение q 0 , а x b - значение q n) и учесть,
что dx hdq.

32.

4
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Пусть n 1 , т.е. имеется всего две точки x0 и
x1 x0 h, в которых известны значения функции
y0 f ( x0 ) и y1 f ( x1 ) . Этим точкам
соответствуют значения 0 и 1 переменной q.
Следовательно,
1
q
x f ( x)dx 0 ( y0 q y0 )hdq h y0q 2 y0
0
0
y1 y0
y0 y1 - формула трапеций
h( y0
) h
2
2
x1
1
2

33.

4
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА

34.

4
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
ПРИБЛИЖЕНИЕ СПЛАЙНАМИ
Сплайном называют кусочно-полиномиальную
функцию, склеенную из различных многочленов,
непрерывную на всем отрезке a, b вместе со
своими несколькими производными. На практике
используют линейные, параболические и
кубические сплайны.
Преимуществом сплайнов перед обычной интерполяцией
является, во-первых, их сходимость и, во-вторых,
устойчивость процесса вычислений.

35.

4
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
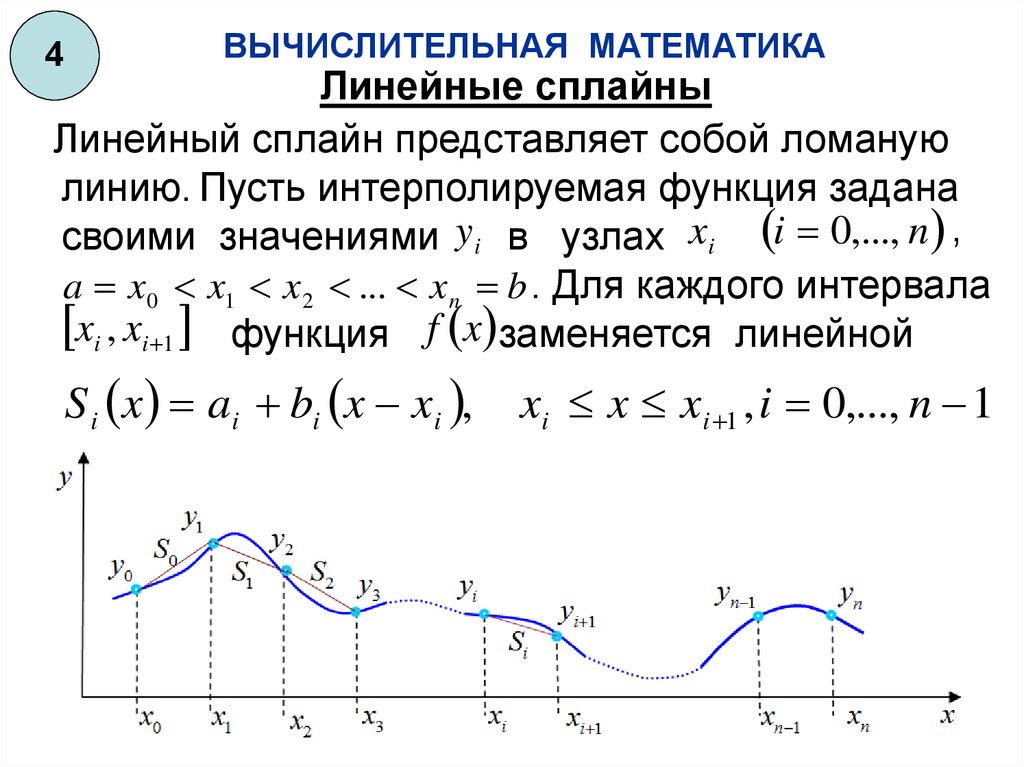
Линейные сплайны
Линейный сплайн представляет собой ломаную
линию. Пусть интерполируемая функция задана
своими значениями yi в узлах xi i 0,..., n ,
a x 0 x1 x 2 ... x n b . Для каждого интервала
xi , xi 1 функция f x заменяется линейной
S i x ai bi x xi ,
xi x xi 1 , i 0,..., n 1

36.

4
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Коэффициенты сплайна a i , bi находят из следующих
условий:
1) в узлах сетки значения сплайна совпадают со
значениями функции f xi y i , т.е. S i xi y i
2) узлах сетки сплайн должен быть непрерывным:
S i xi 1 S i 1 xi 1
Из первого условия находим: a i y i ,
из второго условия получим:
i 0,..., n;
yi 1 yi yi 1 yi i 0,..., n 1; h x x
bi
,
i
i 1
i
xi 1 xi
hi

37.

4
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Параболические сплайны
На каждом интервале x i , xi 1 функция f x
интерполируется квадратичной функцией вида
S i x ai bi x xi ci x xi
2
Здесь мы имеем уже 3n коэффициентов ai , bi , ci ,
i 0,..., n 1определяемых из условий:
1) в узлах сетки значения сплайна совпадают со
значениями интерполируемой функции y i f xi ;
2) в узлах сетки сплайн должен быть непрерывен;

38.

4
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
3) в узлах сетки первая производная должна быть
непрерывна, т.е.
S 'i xi 1 S 'i 1 xi 1

39.

ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
4
Из первого условия получаем a i y i ; i 0,..., n
Из третьего условия получаем
S ' i x bi 2ci x xi ;
S ' i xi bi ; S ' i xi 1 bi 2ci hi bi 1
Отсюда
bi 1 bi
ci
; i 0,..., n 1
2hi

40.

4
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Для того, чтобы вычислить коэффициенты b0 , b1 ,..., bn
надо задать - либо b0 A0 , либо bn An , где A0 , An
значения первой производной функции f x
в точках x x0 и x x n.
Если известно значение b0 A0 , то коэффициенты
bi 1 z i bi , i 0,..., n 1
Если известно, что bn An , то
bn i z n i bn i 1 ; i 1,..., n
В этих формулах
2 yi 1 yi
zi
hi

41.

4
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Кубические сплайны
Построим на [a, b] функцию S ( x) Si ( x),
удовлетворяющую следующим условиям:
а) на каждом отрезке xi , xi 1 i 1, 2,..., n функция
S (x) является многочленом третьей степени;
б) функция S (x), а также ее первая и вторая
производные непрерывны на [a, b] ;
.
в) S ( xi ) f ( xi ), i 0, 1,..., n

42.

ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
4
На каждом интервале функция описывается с.о.:
ci
di
2
S i ( x) a i bi ( x xi ) ( x xi ) ( x xi ) 3 ,
2
6
где a i , bi , ci , d i — коэффициенты, подлежащие
определению.
Поясним смысл введенных коэффициентов.
Имеем
di
S i ( x) bi ci ( x xi ) ( x xi ) 2 ,
2
S i ( x) ci d i ( x xi 0,
S i ( x) d i ,
поэтому
ai S i ( xi ), bi S i ( xi ), ci S i ( xi ),
d i S i ( xi )

43.

4
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА

44.

4
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА

45.

4
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА

46.

4
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА