Похожие презентации:
Численное дифференцирование
1.
Численное дифференцированиеДАНО y=f(x)
НАЙТИ f‘ (x)
Когда применяется?
1. Дифференцирование таблично заданной функции
2. Вычисление производной в процессе численного счета
3. Упрощение аналитически заданной функции
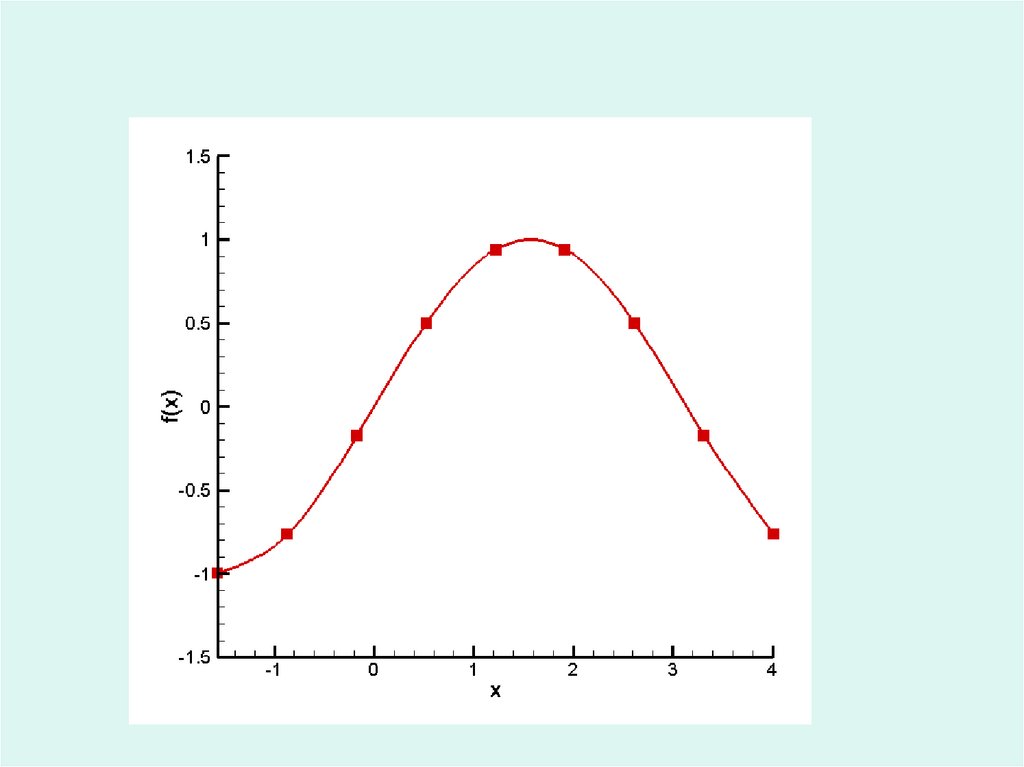
Конечно-разностная аппроксимация
x xi
f fi
f x x f x
f x lim
x 0
x
2.
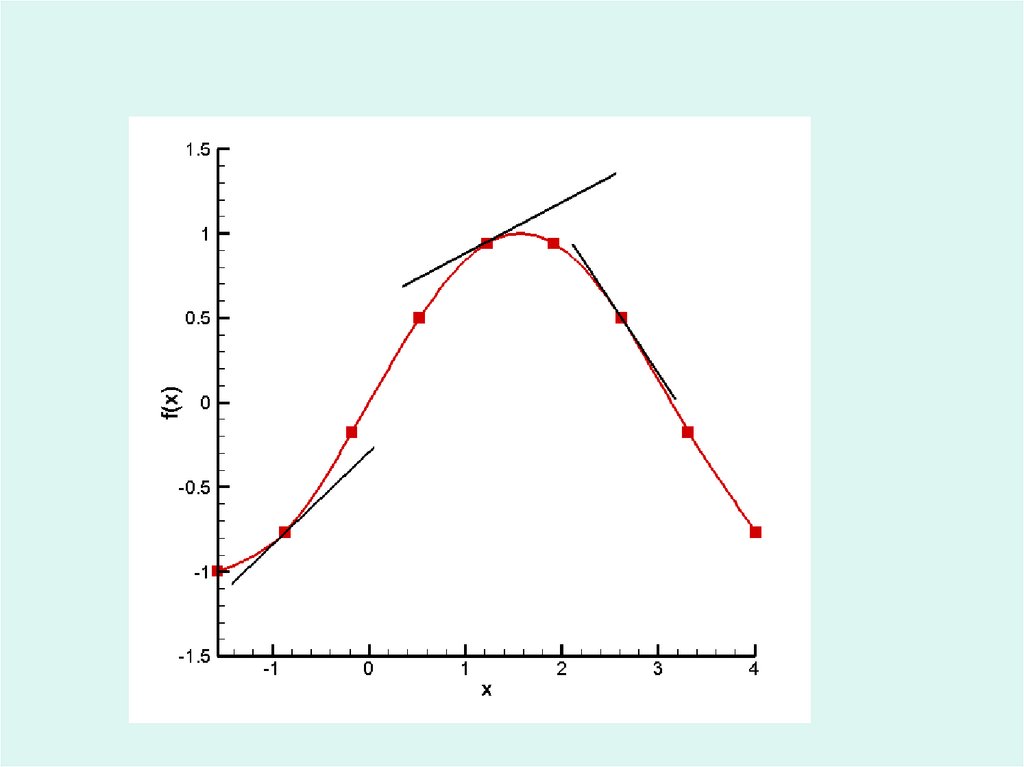
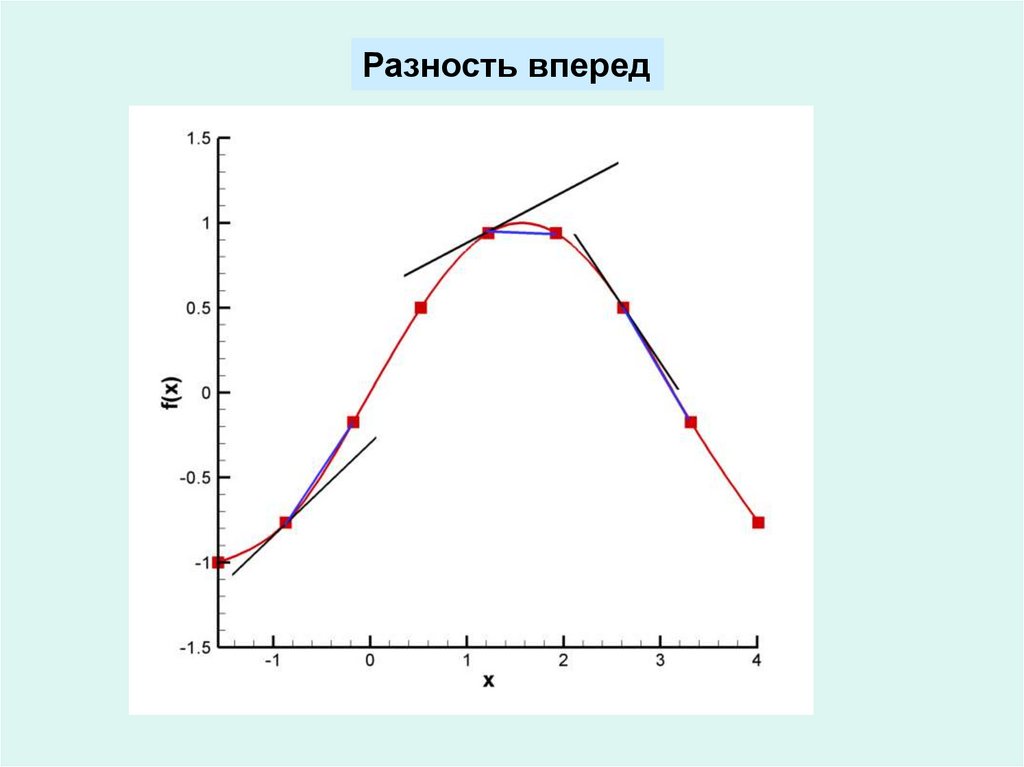
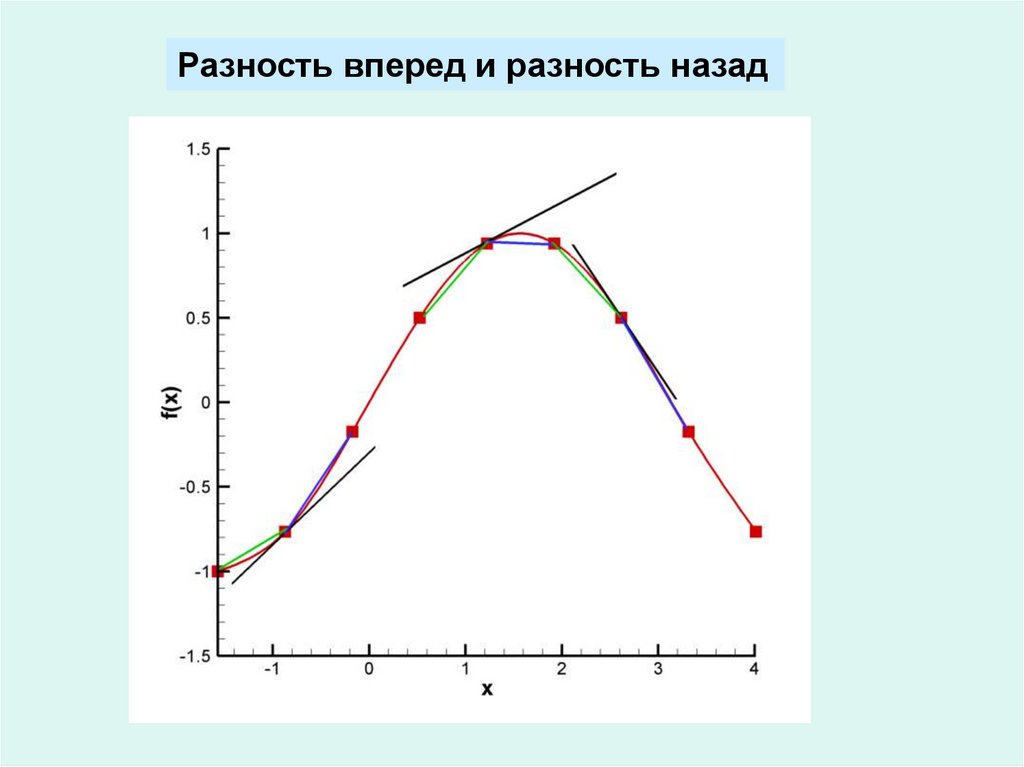
Разность вперед:f xi Lh
f i 1 f i
h
Разность назад:
f xi Lh
f i f i 1
h
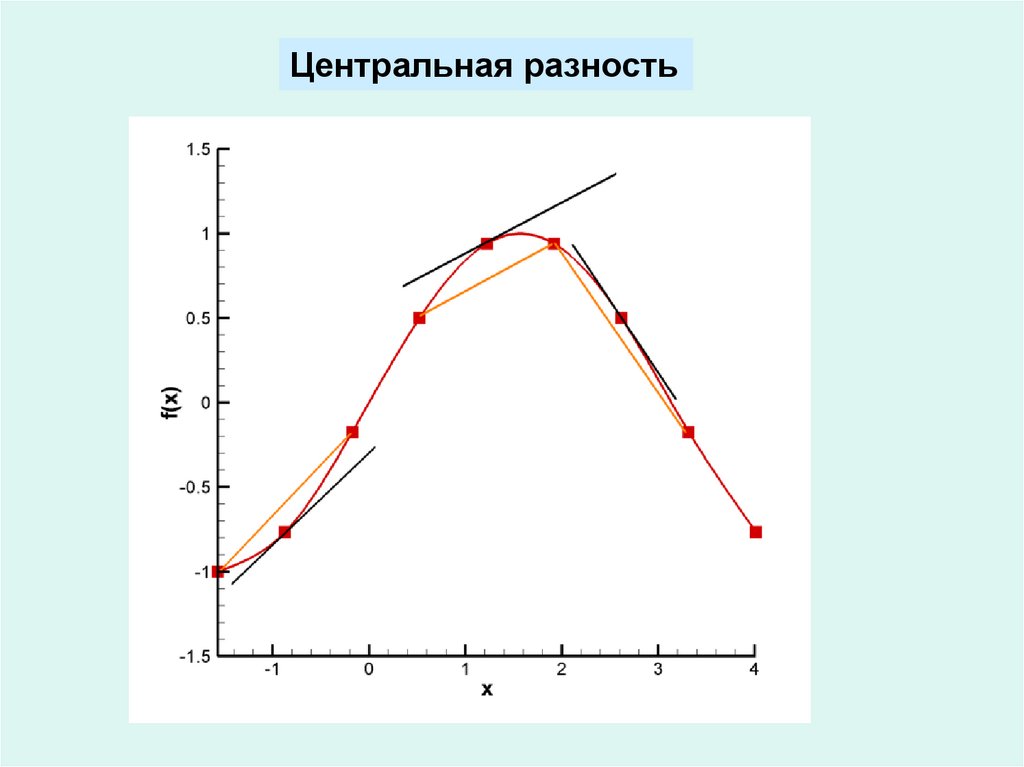
Центральная разность:
Lh Lh
f i 1 f i 1
f xi Lh
2
2h
0
3.
4.
5.
Разность вперед6.
Разность вперед и разность назад7.
Центральная разность8. Погрешность аппроксимации
Погрешностьюаппроксимации
называется разность
n-ой
производной
x f n x L hn
Оценка погрешности формулы «разность вперед»
f i 1 f i
xi
h
Разложим функцию f(x) в ряд Тэйлора:
h2
h3
f i 1 f ( xi 1 ) f ( xi h) f i hf i
f i
f i ...,
2
6
Подставим в формулу:
Главный член погрешности
f '
h2
h3
fi hfi
fi
fi ... fi
2
h
h
2
6
f ' xi
fi fi
fi ...
h
2
6
9.
Оценка погрешности формулы «центральная разность»f '
fi 1 fi 1
xi
2h
h2
h3
f i 1 f i hf i
f i
f i ...,
2
6
h2
h3
f i 1 f i hf i
f i
f i ....
2
6
h2
h3
h2
h3
f i hf i
f i
f i ... f i hf i
f i
f i ...i
2
6
2
6
f ' xi
2h
h2
f i
f i ...
6
Главный член погрешности
10.
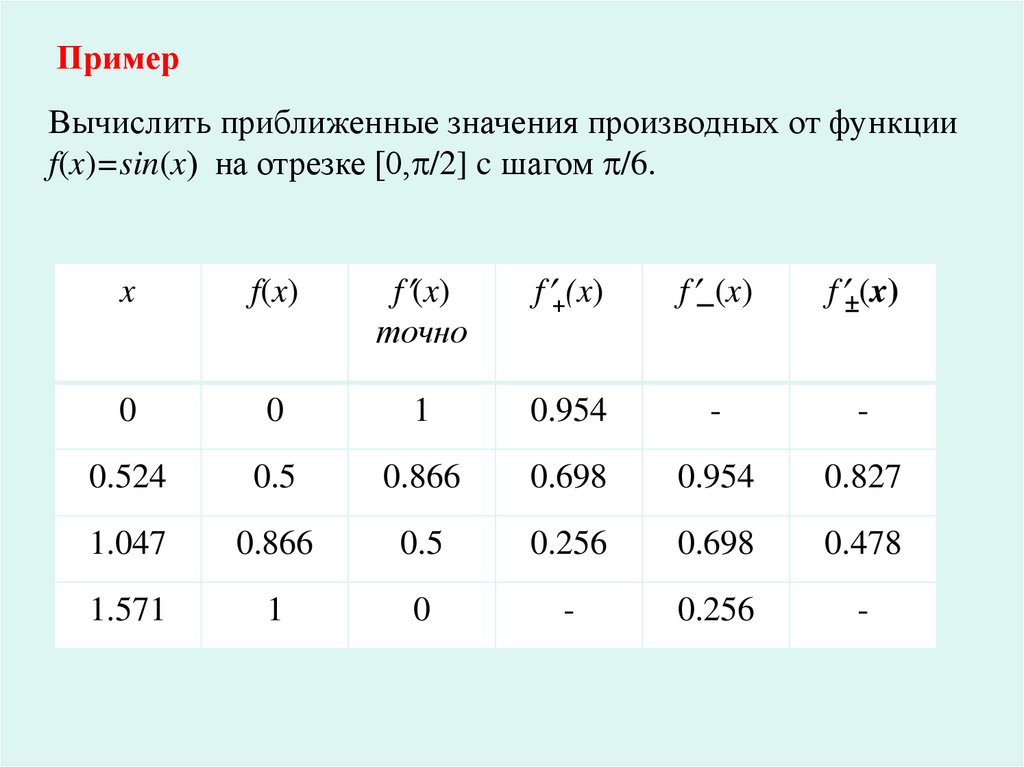
ПримерВычислить приближенные значения производных от функции
f(x)=sin(x) на отрезке [0, /2] c шагом /6.
x
f(x)
f (x)
точно
f +(x)
f _(x)
f (x)
0
0
1
0.954
-
-
0.524
0.5
0.866
0.698
0.954
0.827
1.047
0.866
0.5
0.256
0.698
0.478
1.571
1
0
-
0.256
-
11.
Метод неопределенных коэффициентовКак получить формулы для вычисления производных в
любой точке сетки с любым порядком точности?
f x0
f 0 f1 f 2
h
, , - неопределенные коэффициенты
Разложим f1, f2 в ряд Тэйлора:
h2
h3
f1 f 0 hf 0
f o
f 0 ...,
2
6
3
4
h
f 2 f 0 2hf 0 2h 2 f 0
f 0 ....
3
f0
4
2
f ' x0 ( ) f 0 ( 2 ) hf 0 ( 2 ) h f ( ) ...
h
2
6
3
12.
02 1
2 0
2
.
f x0
3
1
, 2,
2
2
3 f 0 4 f1 f 2
ch 2
2h
3 f N 4 f N 1 f N 2
f x N
ch 2
2h
13.
Примерf x0
3 f 0 4 f1 f 2
ch 2
2h
f x N
3 f N 4 f N 1 f N 2
ch 2
2h
№ п/п
x
f(x)
f (x) точно
0
0
0
1
1
0.524
0.5
0.866
2
1.047
0.866
0.5
3
1.571
1
0
f ' 0
3 0 4 0.5 0.866
1.083
1.047
Точное значение = 1
3 1 4 0.866 0.5
0.034
1.047
Точное значение = 0
f ' 1.571
14.
Формулы для второй производнойfi 1 fi fi fi 1
f
f
fi 1 2 fi fi 1
''
h
h
i
i
1
f xi
h
h
h2
Формула имеет второй порядок точности
.
15.
Численное решение обыкновенныхдифференциальных уравнений (ОДУ)
ОДУ называются такие уравнения, которые содержат одну
или несколько производных от искомой функции
F x, y, y , y ,..., y n 0
n – порядок уравнения
Решение имеет вид:
y x, c1 , c 2 ,..., c n
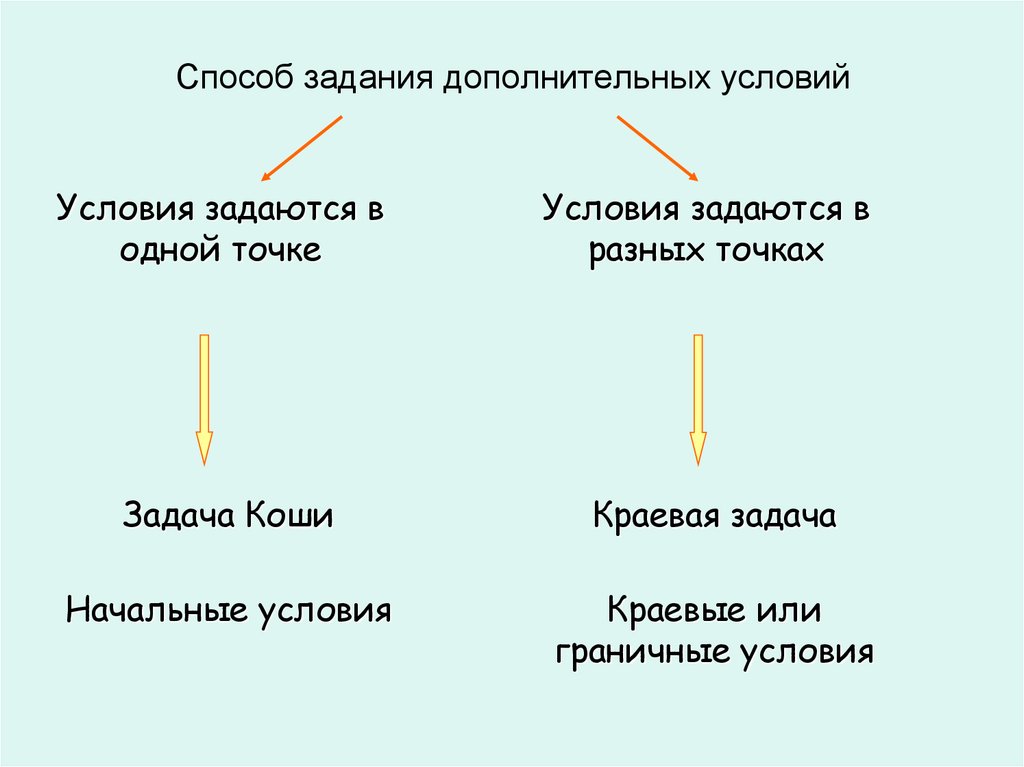
16. Способ задания дополнительных условий
Условия задаются водной точке
Условия задаются в
разных точках
Задача Коши
Краевая задача
Начальные условия
Краевые или
граничные условия
17.
ЗАДАЧА КОШИdy
x2 y3,
dx
2
d y dy
2
xy ,
2
dx
dx
;
y 1 1
y 1 1,
y 1 0
КРАЕВАЯ ЗАДАЧА
d3y
d 2 y dy
x x 2 ,
3
dx
dx
dx
y 1 0,
d2y
dy
2 y sin x ,
2
dx
dx
y 1 0,
y 0 1,
y ' ' 3 2
y ' 1 0
18.
Приближенные методы решения задачи Коши дляОДУ первого порядка
dy
Дано
f x, y
dx
Найти решение y(x) на отрезке x 0 , x n
y x 0 y 0
Будем искать приближенное решение в узлах расчетной
сетки
x i x 0 ih, i 0,1,..., n
x n x0
с шагом h
n
Необходимо найти приближенные значения в узлах сетки
yi=y(xi)
19.
dyf x, y
Интегрируем уравнение
dx
на отрезке
x , x
i 1
i
xi 1
yi 1 yi f x, y dx
xi
,
Для вычисления интеграла воспользуемся
квадратурной формулой численного интегрирования,
например, формулой левых прямоугольников:
xi 1
f x, y dx hf x , y
i
i
xi
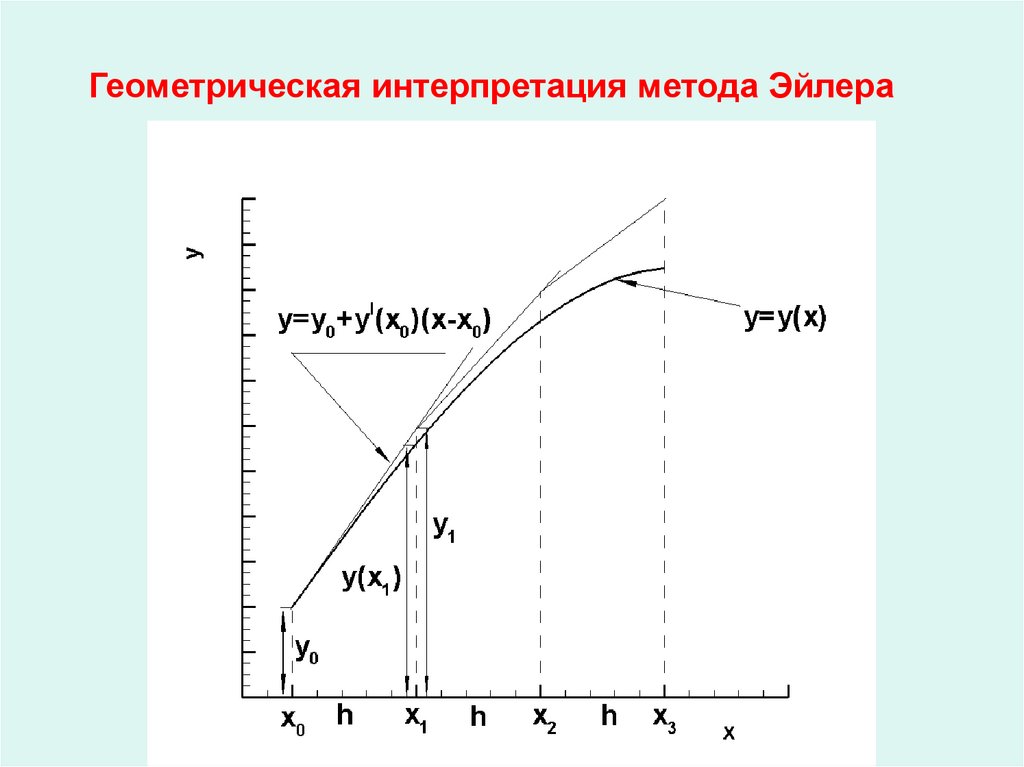
yi 1 yi hf xi , yi
i 0,1,..., n 1
ФОРМУЛА ЭЙЛЕРА
20. Геометрическая интерпретация метода Эйлера
21.
Для вычисления интеграла воспользуемся теперьформулой правых прямоугольников:
xi 1
f x, y dx hf x , y
i 1
i 1
xi
,
yi 1 yi hf xi 1 , yi 1
i 0,1,..., n 1
НЕЯВНАЯ ФОРМУЛА ЭЙЛЕРА
Формулы Эйлера имеют первый порядок аппроксимации.
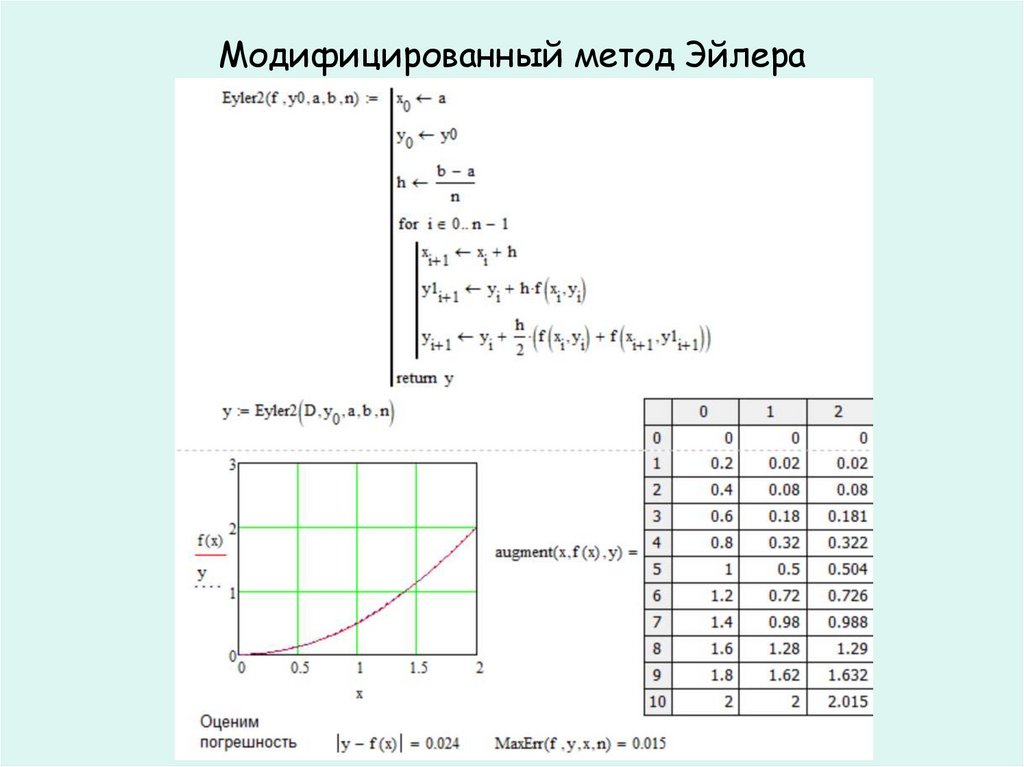
22. Модифицированный метод Эйлера (метод предиктор-корректор – «предсказать-исправить»)
Два этапа~
yi 1 yi hf xi , yi
h
yi 1 yi f xi , yi f xi 1 , ~
yi 1
2
Второй порядок аппроксимации
23. Пример
Решить задачу Коши методами Эйлера и модифицированнымметодом Эйлера
24.
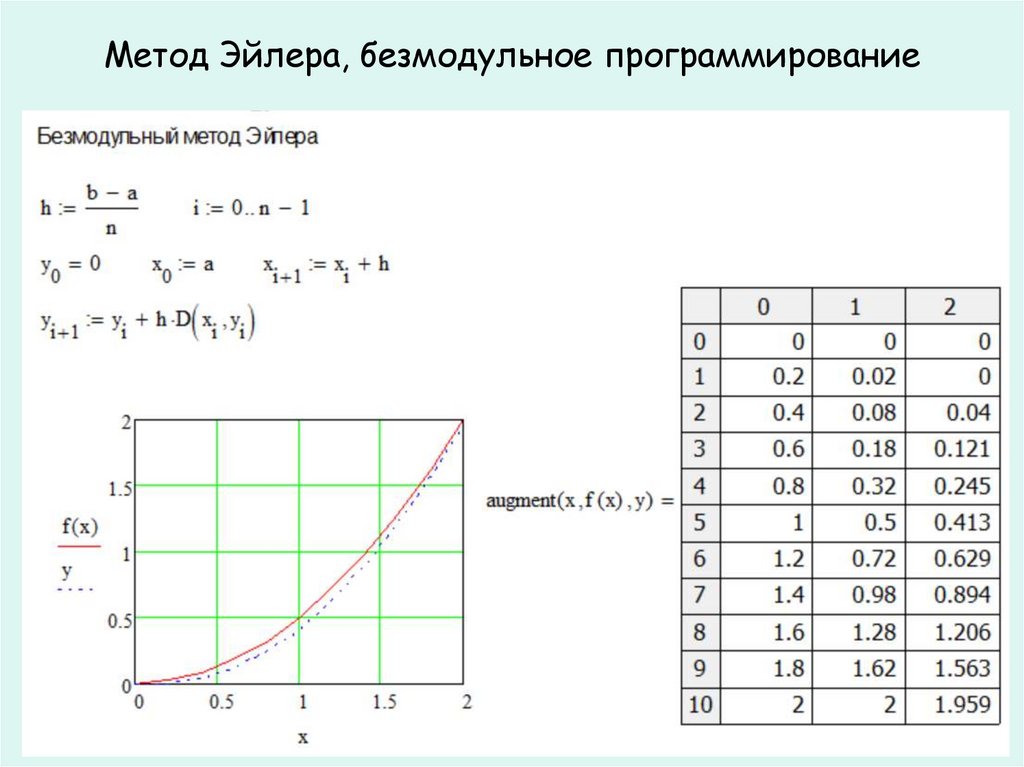
Метод Эйлера, безмодульное программирование25.
Метод Эйлера, модульное программирование26.
Модифицированный метод Эйлера27.
Методы Рунге-Куттыyi 1 yi h xi , yi , h
Решение ищется в виде
q
xi , yi , h cn k ni h
n 1
где
k1i h f xi , yi
k2i h f xi 2 h, yi 21k1i h
k3i h f xi 3h, yi 31k1i h 32 k2i h
…
k qi h f xi q h, yi q1k1i h ... q , q 1k qi 1 h
Здесь
n , nj ,0 j n q
фиксированные числа (параметры), которые
подбираются так, чтобы получить требуемый
порядок аппроксимации (точности)
28.
Методы Рунге-Кутты второго порядка точностиk 1i f xi , yi ,
h
h i
k f xi , yi
k1
2a
2a
i
2
а – параметр
yi 1 yi h 1 a k 1i ak2i .
при а=1/2
k 1i f xi , yi ,
k2i f xi h, yi hk1i
yi 1 yi
Модифицированный
метод Эйлера
h i
k 1 k2i , i 0, 1, 2 ,...
2
29.
Методы Рунге-Кутты второго порядка точностипри а=1
k 1i f xi , yi ,
h
h i
k f xi , yi k1
2
2
i
2
yi 1 yi hk2i , i 0, 1, 2 ,...
Метод средней точки
30.
Методы Рунге-Кутты четвертого порядка точностиk1i f xi , yi ,
i
h
hk
i
1
,
k 2 f xi , yi
2
2
i
h
hk
i
2
,
k3 f xi , yi
2
2
k 4i f xi h, yi hk3i ,
h i
yi 1 yi k1 2k 2i 2k3i k 4i , i 0,1,2,...
6
31. Пример
Решить задачу Коши c помощью четырехшагового методаРунге-Кутты
32.
Решение задачи Коши в Mathcad (функция rkfixed)Функция Mathcad rkfixed вычисляет матрицу из двух столбцов
– первый столбец значения аргумента х, второй – значения,
вычисленные четырехшаговым методом Рунге-Кутты:
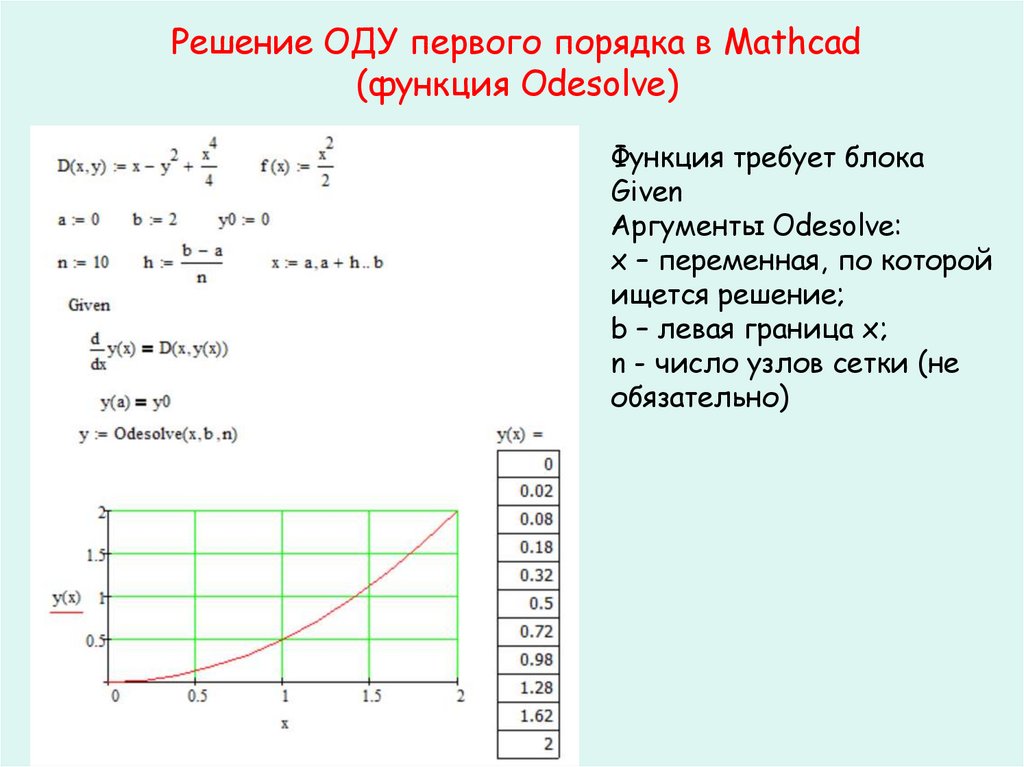
33. Решение ОДУ первого порядка в Mathcad (функция Odesolve)
Функция требует блокаGiven
Аргументы Odesolve:
х – переменная, по которой
ищется решение;
b – левая граница х;
n - число узлов сетки (не
обязательно)
.
.
.
34. Методы приближенного решения задачи Коши для системы ОДУ и ОДУ высших порядков Обобщение метода Эйлера для решения систем ОДУ
первого порядкаdy
x , y , z
dx
dz x, y , z
dx
y x0 y0 , z x0 z0
yi 1 yi h xi , yi , zi
zi 1 zi h xi , yi , zi
35. Обобщение модифицированного метода Эйлера для решения систем ОДУ первого порядка
~y i 1 y i h x i , y i , z i
~
z i 1 z i h x i , y i , z i
,
h
yi 1 yi xi , yi , zi xi , ~
yi , ~
zi
2
h
zi 1 zi xi , yi , zi xi , ~
yi , ~
zi
2
36. Четырехшаговый метод Рунге-Кутта для решения систем ОДУ первого порядка
hyi 1 yi k1 2k2 2k3 k4
6
h
zi 1 zi l1 2l2 2l3 l4
6
k1 xi , yi , zi ,
l1 xi , yi , zi ,
h
hk1
hl1
k2 xi , yi
, zi
,
2
2
2
h
hk1
hl1
l2 xi , yi
, zi
,
2
2
2
37. Четырехшаговый метод Рунге-Кутта для решения систем ОДУ первого порядка
hl2hk2
h
, zi
k3 xi , yi
,
2
2
2
hl2
hk2
h
, zi
l3 xi , yi
,
2
2
2
k4 xi h, yi hk3 , zi hl3 ,
l4 xi h, yi hk3 , zi hl3
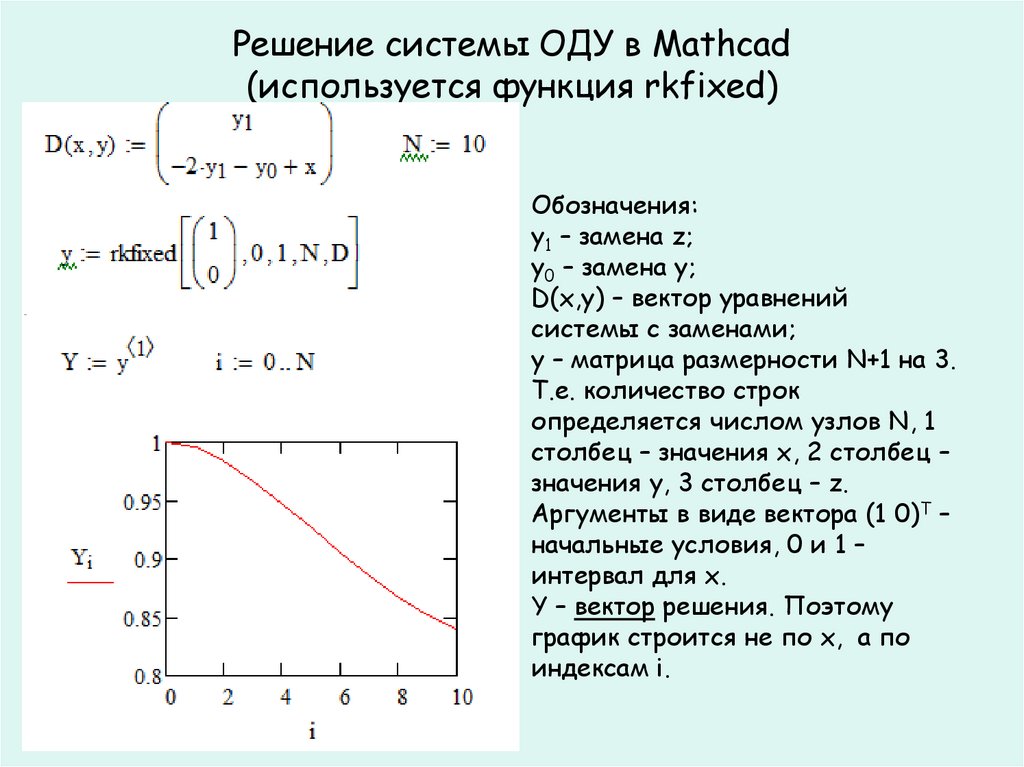
38. Решение системы ОДУ в Mathcad (используется функция rkfixed)
..
.
Обозначения:
y1 – замена z;
y0 – замена y;
D(x,y) – вектор уравнений
системы с заменами;
y – матрица размерности N+1 на 3.
Т.е. количество строк
определяется числом узлов N, 1
столбец – значения х, 2 столбец –
значения y, 3 столбец – z.
Аргументы в виде вектора (1 0)Т –
начальные условия, 0 и 1 –
интервал для х.
Y – вектор решения. Поэтому
график строится не по х, а по
индексам i.
39. Решение ОДУ второго порядка
d2ydy
f
x
,
y
,
,
2
dx
dx
dy
x0 z0
y x0 y0 ,
dx
Обозначим z x dy
dx
Тогда уравнение сводится к системе двух уравнений
dy
dx z х
dz f x, y, z ,
dx
.
y x0 y0 ,
z x0 z0
Эту систему можно решать как показано выше, с помощью функции rkfixed.
Другой вариант решения ОДУ второго порядка
– использование вычислительного блока Given…Odesolve
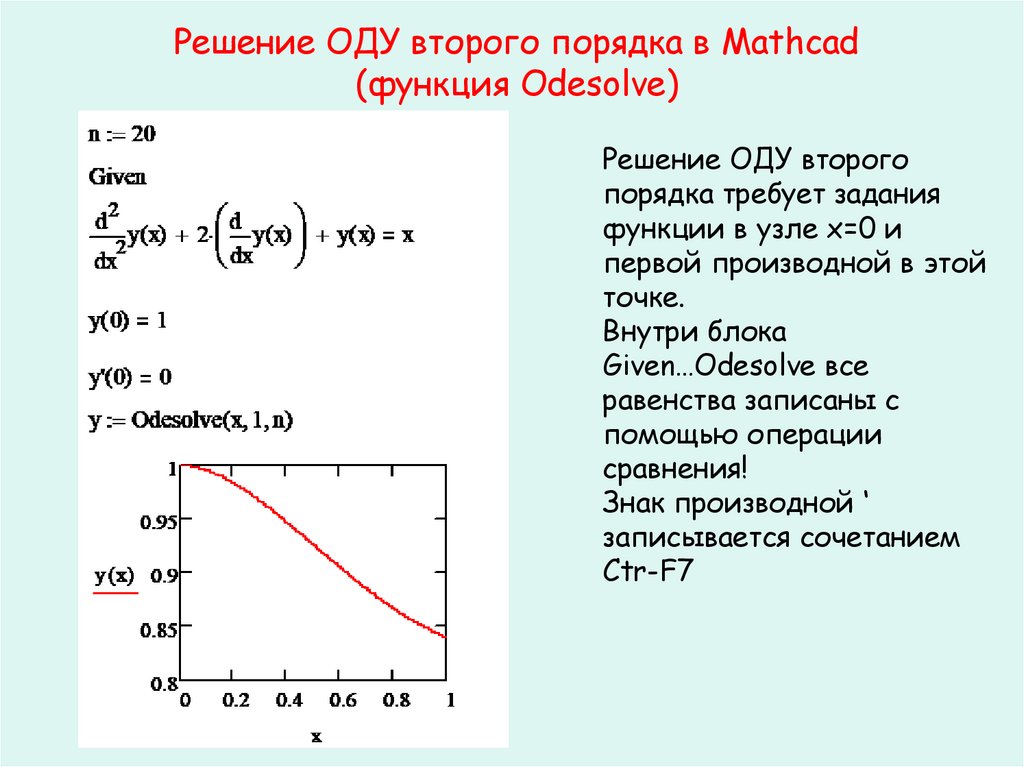
40. Решение ОДУ второго порядка в Mathcad (функция Odesolve)
..
.
Решение ОДУ второго
порядка требует задания
функции в узле х=0 и
первой производной в этой
точке.
Внутри блока
Given…Odesolve все
равенства записаны с
помощью операции
сравнения!
Знак производной ‘
записывается сочетанием
Ctr-F7





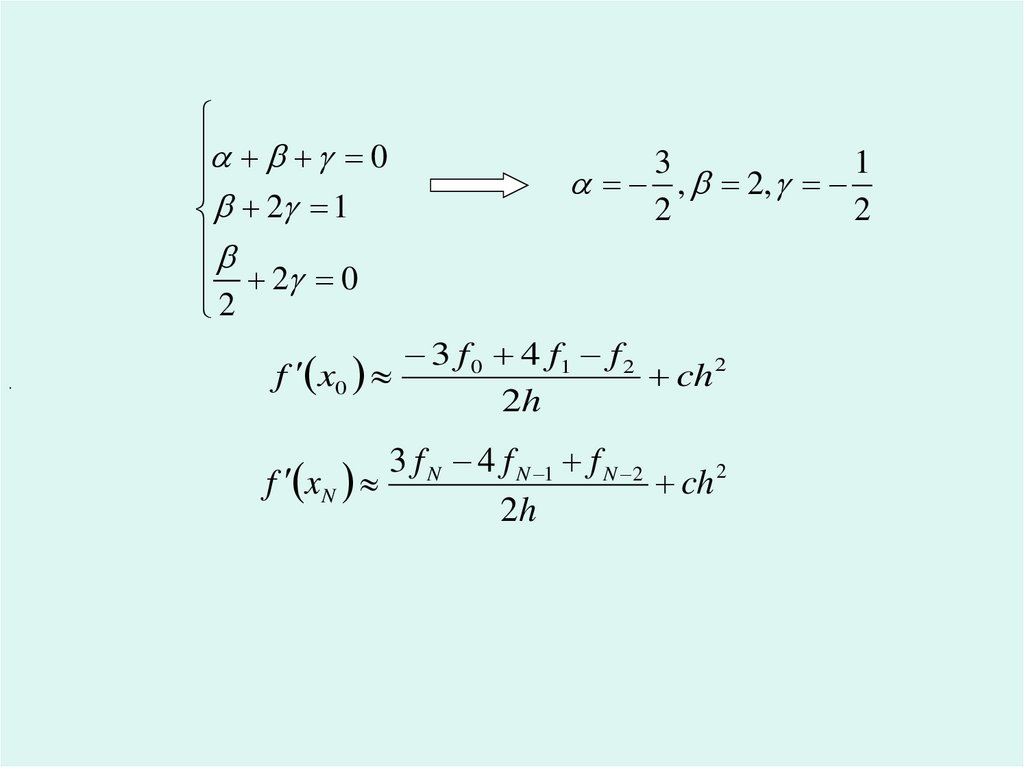





















 Математика
Математика








