Методическая разработка темы: «Показательная функция»

1. Методическая разработка темы: «Показательная функция»

2. Содержание

• Показательная функция
• Показательные уравнения
• Показательные неравенства
• Типовые задачи
• Тесты
• Домашняя контрольная работа

3. Показательная функция

Определение
Свойства
График.
Содержание

4. Определение

Показательная функция – это
x
функция вида
,
y a
где x – переменная,
a - заданное число, a >0, a 1.
Примеры:
у 3 ;
х
х
1
у ;
2
у 0,4
х
к теме

5. Свойства показательной функции

Свойства показательной
х
функции у а
1. Область определения:
все действительные числа
D(y) = R;
2. Множество значений:
все положительные числа
E(y) = (0; + ∞);
3. При a > 1 функция возрастающая;
при 0 < a < 1 функция убывающая.
к теме

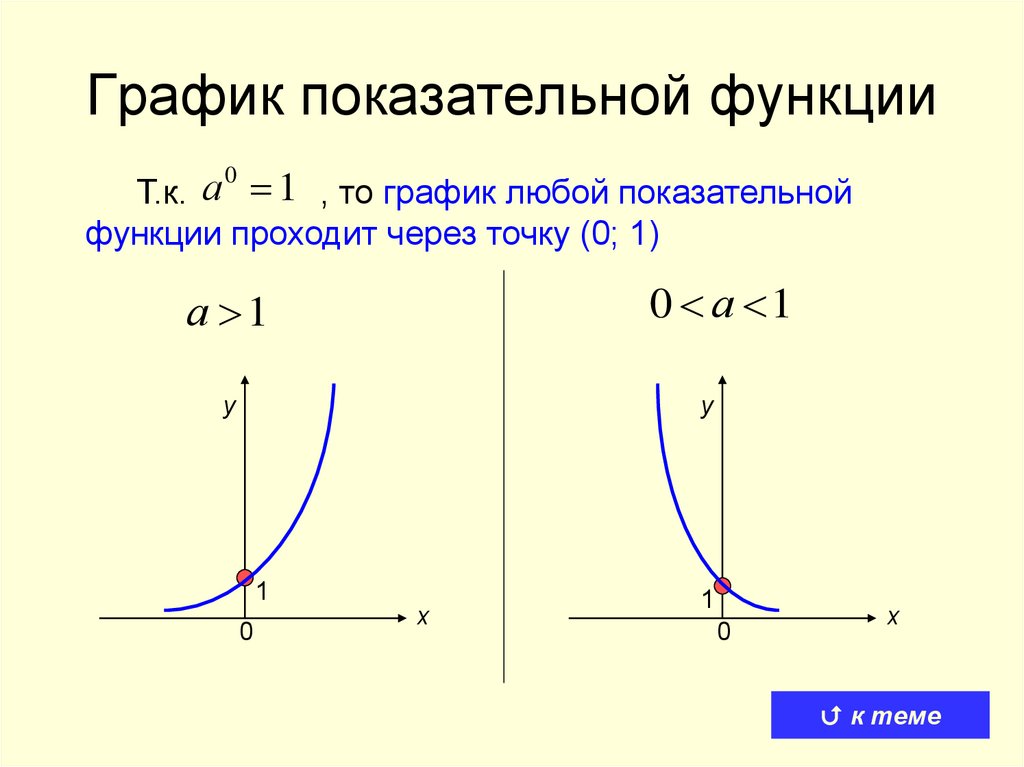
6. График показательной функции

Т.к. а 1 , то график любой показательной
функции проходит через точку (0; 1)
0
а 1
0 а 1
у
у
1
0
х
1
0
х
к теме

7. Показательные уравнения

Определение
Простейшие
уравнения
Способы решения
сложных уравнений
Содержание

8. Определение

Уравнение, в котором
переменная содержится в
показателе степени, называется
показательным.
Примеры:
2 8; 9 5 3 6 0
х
х
х
к теме

9. Простейшее показательное уравнение – это уравнение вида

a a , где a 0, a 1.
x
b
Простейшее показательное
уравнение решается с
использованием свойств степени.
a a x b
x
b
к теме

10.

Способы решения сложных
показательных уравнений.
Замена
переменной
Деление на
показательную
функцию
Вынесение
за скобки
степени с
меньшим
показателем
к теме

11. Вынесение за скобки степени с меньшим показателем

Данный способ используется,
если соблюдаются два условия:
1) основания степеней
одинаковы;
2) коэффициенты перед
переменной одинаковы
Например:
2
x 1
4 2
решение
x 2
32

12. Замена переменной

При данном способе показательное
уравнение сводится к квадратному.
Способ замены переменной используют, если
а) основания степеней одинаковы;
б) показатель одной из коэффициенты перед
степеней в 2 раза
переменной
больше, чем
противоположны.
у другой.
Например:
Например:
х
2x
2-х
х–1
3 – 4 · 3 – 45 = 0
2
–2
=1
решение
решение

13. Деление на показательную функцию

Данный способ используется, если
основания степеней разные.
x
x
=5 |:5
x
а) в уравнении вида a = b делим на b
Например: 2
х
х
x
решение
б) в уравнении A a + B (ab) + C b = 0
2x
x
2x
2x
делим на b .
Например:
х
х
х
решение
3 25 - 8 15 + 5 9 = 0 | : 9
x

14.

Показательные неравенства
Определение
Простейшие
неравенства
Решение неравенств
Содержание

15. Определение

Показательные неравенства –
это неравенства, в которых
неизвестное содержится в
показателе степени.
Примеры:
3 9;
х
2 5 2
х
х 1
11
к теме

16. Простейшие показательные неравенства – это неравенства вида:

a a
b
a a
b
x
x
a a
x
b
a a
x
b
где a > 0, a 1, b – любое число.
к теме

17.

При решении простейших
неравенств используют свойства
возрастания или убывания
показательной функции.
a a
x b
a 1
x
b
a a
x b
0 a 1
x
b
Для решения более сложных
показательных неравенств используются те
же способы, что и при решении
показательных уравнений.
к теме

18. Типовые задачи

• Показательная функция
• Показательные уравнения
• Показательные неравенства
Содержание

19.

• Построение графика
• Сравнение чисел с использованием свойств
показательной функции
• Сравнение числа с 1
а) аналитический способ;
б) графический способ.
типовые задачи

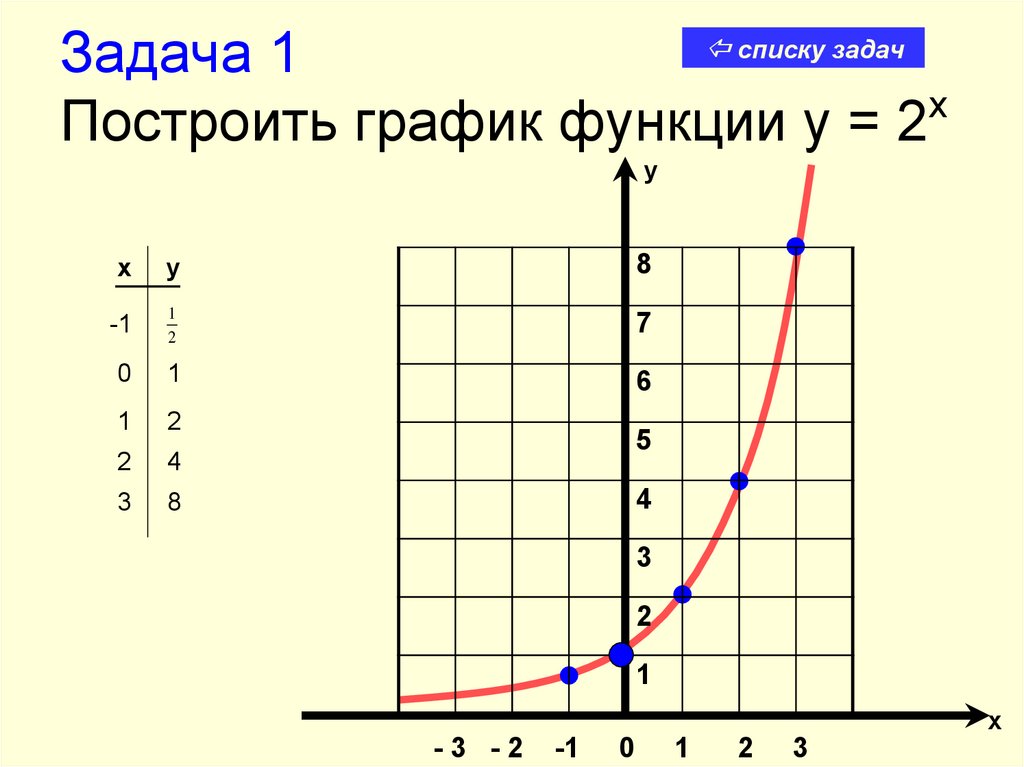
20. Задача 1 Построить график функции y = 2x

списку задач
Задача 1
x
Построить график функции y = 2
у
x
y
8
-1
1
2
7
0
1
6
1
2
2
4
3
8
5
4
3
2
1
х
-3 -2
-1
0
1
2
3

21. Задача 2 Сравнить числа

Задача 2
1
1
и
Сравнить числа 3 3
2
списку задач
1, 4
Решение
1
3
2 1,41... 1,4
1
0 1
3
Ответ:
1
3
2
1, 4
1
3
2
1, 4
1
3

22. Задача 3 Сравнить число с 1.

списку задач
Задача 3
5
Сравнить число 3 с 1.
Решение
1 3
0
-5 < 0
5
3 3
3 1
Ответ: 3 5 1
0
3 5 1

23. Задача 4 Cравнить число р с 1

р=2
3
2 > 1, то
t
функция у = 2 –
возрастающая.
3
Ответ: 2 > 1.
списку задач
1
р = 2
4
1
0 < 2 < 1, то
функция у =
– убывающая
4
1
Ответ: > 1
2

24.

• Простейшие показательные уравнения
• Уравнения, решаемые вынесением за скобки
степени с меньшим показателем
• Уравнения, решаемые заменой переменной
случай 1;
случай 2.
• Уравнения, решаемые делением на
показательную функцию
случай 1;
случай 2.
типовые задачи

25. Простейшие показательные уравнения

Простейшие показательные
списку задач
уравнения
1). 23 x 4 2 x 7 3х 4 х 7
3х х 7 4 2х 11 х 5,5.
Ответ: - 5,5.
2). 5
x 2 3 x
1 5
х 2 3 х
2
х
3х 0
5
0
х 0,
х х 3 0
х 3.
Ответ: 0; 3.

26. Вынесение за скобки степени с меньшим показателем

Вынесение за скобки степени с
списку задач
меньшим показателем
2
x 1
4 2
x 2
32
2 х 2 ( 23 4 1) 32
x + 1 - (x - 2) =
=x+1–x+2=3
2 х 2 (8 4) 32
2 х 2 4 32 | : 4
2 х 2 8
2 х 2 23
х 2 3
х 5
Ответ: 5
к теории

27. Замена переменной (сл.1)

списку задач
основания степеней одинаковы, показатель одной из
степеней в 2 раза больше, чем у другой .
х
2x
3 – 4 · 3 – 45 = 0
t = 3x (t > 0)
t 2 – 4t – 45 = 0
По т. Виета: t1· t 2 = - 45; t1+ t 2 =4
t1 = 9; t 2 = - 5 – посторонний корень
x
x
2
3 = 9; 3 = 3 ; x = 2.
Ответ: 2
к теории

28. Замена переменной (сл. 2)

списку задач
Основания степеней одинаковы,
коэффициенты перед переменной противоположны.
2
2 х
2
х
х 1
1
1
2 2 2 2 1
2
х
t 2 t 0
x
4 t
1
t 2
8 t 2t
2
t 2t 8 0
2
По т. Виета:
t1 t2 8, t1 t2 2
t1 4 - посторонний корень
t2 2
x
2 2
х 1
Ответ: 1
к теории

29. Деление на показательную функцию

а) 2 5 |: 5
х
х
списку задач
x
х
2
1
5
х
2 2
5 5
0
х 0
Ответ: 0
к теории

30. Деление на показательную функцию

3 25 х 8 15 х 5 9 х 0 : 9 х
3 52 х 8 5 x 3 x
5 0
2х
2x
3
3
2x
x
5
5
3 8 5 0
3
3
5
t
3
х
(t 0)
списку задач
3t 2 8t 5 0
D 64 4 3 5 4 2 2
8 2 10 5
t1
;
6
6 3
8 2
t2
1.
6
х
х
5
5
3
3
5
1
3
х 1
5 5
3 3
х
х 0
3t 8t 5 0
2
Ответ: 0; 1.
к теории
0

31.

• Простейшие показательные
неравенства
• Двойные неравенства
• Неравенства, решаемые вынесением за
скобки степени с меньшим показателем
• Неравенства, решаемые заменой
переменной
типовые задачи

32. Простейшие показательные неравенства

списку задач
Простейшие
показательные неравенства
1). 3 9 3 3 x 2
х
x
2
Ответ : х 2.
х
x
1
1 1
1
2).
4
2
2 2
Ответ : х 2.
2
x 2

33. Двойные неравенства

1
33 x 9
3
1
3 x
3 3 3
3 > 1, то 1 3 x 2
2
1 3 x 2 3
4 x 1
Ответ: (- 4; -1).
списку задач

34. Решение показательных неравенств

списку задач
Решение
показательных неравенств
Метод: Вынесение за скобки степени с меньшим
показателем
3
3
х 3
х 3
3
3
1 х
3 10
3
1 3
(1 3 ) 10
3
х 3
(1 9) 10
х 3
10 10 : 10
х 3
1
х 3
0
3
3
3 > 1, то х 3 0
3
х 3.
Ответ: х >3

35. Решение показательных неравенств

Метод: Замена переменной
1
3 (t 4) t 0
3
3 9 11 3 4
х
х
3 3 11 3 4 0
2х
списку задач
х
3 t (t 0)
2
3t 11t 4 0
х
D 11 4 3 ( 4) 121 48 169 13
2
11 13 2 1
t1
2 3
6 3
t2
11 13 24
4
6
6
2
1
1
x
0 t ;0 3
3
3
1
3 3 ;
х
3>1, то
х 1.
Ответ: х < -1.

36. Тесты по темам:

• Показательная функция и её свойства
• Показательные уравнения
• Показательные неравенства
Содержание

37. Литература

• 1). Ш. А. Алимов. Алгебра и начала
анализа: Учеб. Для 10-11 кл.
общеобразоват. учреждений., М. :
Просвещение, 2007.
• 2). Г. В. Дорофеев. Сборник заданий
для проведения письменного экзамена
по математике за курс средней школы,
М.: ООО «Дрофа», 2002.