Решение систем двух линейных уравнений с двумя переменными с помощью определителей

1. Решение систем двух линейных уравнений с двумя переменными с помощью определителей

2. 1. Умножим первое уравнение на b2, а второе уравнение на ­b1 и сложим эти уравнения

-общий вид системы линейных
уравнений с двумя неизвестными
Если
, то находим х:

3. 2. Аналогично, умножим первое уравнение на –а2, а второе – на а1 и сложим эти уравнения

Если
, то находим y:

4.

-главный определитель системы линейных
уравнений с двумя неизвестными

5. Вспомогательные определители

Определитель Δₓ получается из главного определителя системы
заменой первого столбца столбцом свободных членов, второй столбец
оставляем таким же.
Определитель Δу получается из главного определителя системы
заменой второго столбца столбцом свободных членов. первый столбец
оставляем таким же, как в главном определителе системы,

6. Решение системы

Если Δ≠0, то система имеет единственное решение
(x,y), которое находится по формулам Крамера:
- формулы Крамера для решения
системы
двух
линейных
уравнений с двумя переменными.
Если Δ=0, Δy≠0, Δₓ≠0, то система не имеет решений.
Если Δ=Δy=Δₓ=0, то система имеет бесконечное
множество решений.

7.

Некоторые свойства определителей
2-го порядка
Свойство 1. Определитель не изменится, если его строки
поменять местами с соответствующими столбцами
Свойство 2. При перестановке двух строк (столбцов)
определитель изменит знак на противоположный,
сохраняя абсолютную величину.
Свойство 3. Определитель с двумя одинаковыми
строками (или столбцами) равен нулю.
Свойство 4. Определитель, у которого элементы двух
строк (столбцов) соответственно пропорциональны,
равен нулю.

8.

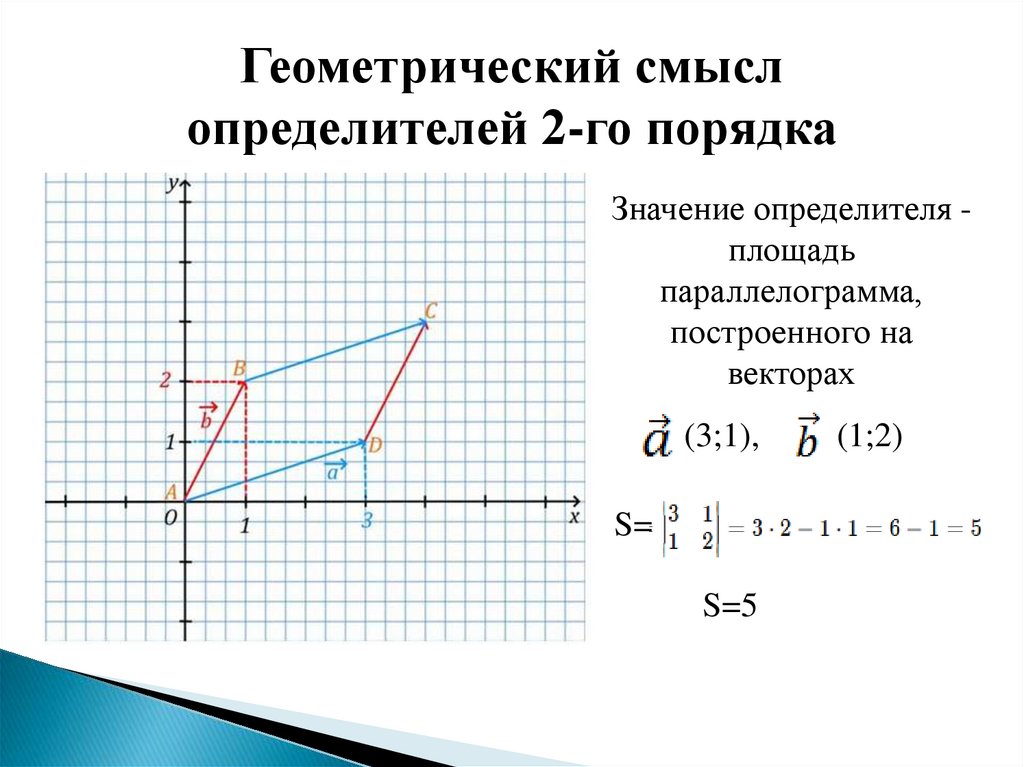
Геометрический смысл
определителей 2-го порядка
Значение определителя площадь
параллелограмма,
построенного на
векторах
(3;1),
S=
S=5
(1;2)

9. Домашнее задание: 1. Вычислить значение определителей

2) Решить систему уравнений двумя способами, способом
сложения и способом подстановки:
а)
б)
3) Решить систему уравнений: