Похожие презентации:
Построение сечений
1.
Методыпостроения
Проект Габрусевич Ксении
сечений многогранников
2.
Содержание проекта1 Что такое сечение многогранника
2 Методы построений многогранников:
2.1 Аксиоматический
2.1.1 Метод следов
2.1.2 Метод вспомогательных сечений
2.2 Комбинированный
2.2.1 Построение сечения, проходящего
через заданную прямую параллельную
другой заданной прямой.
2.2.2 Построение сечения, проходящего через
заданную точку параллельно двум заданным
скрещивающимся прямым.
3.
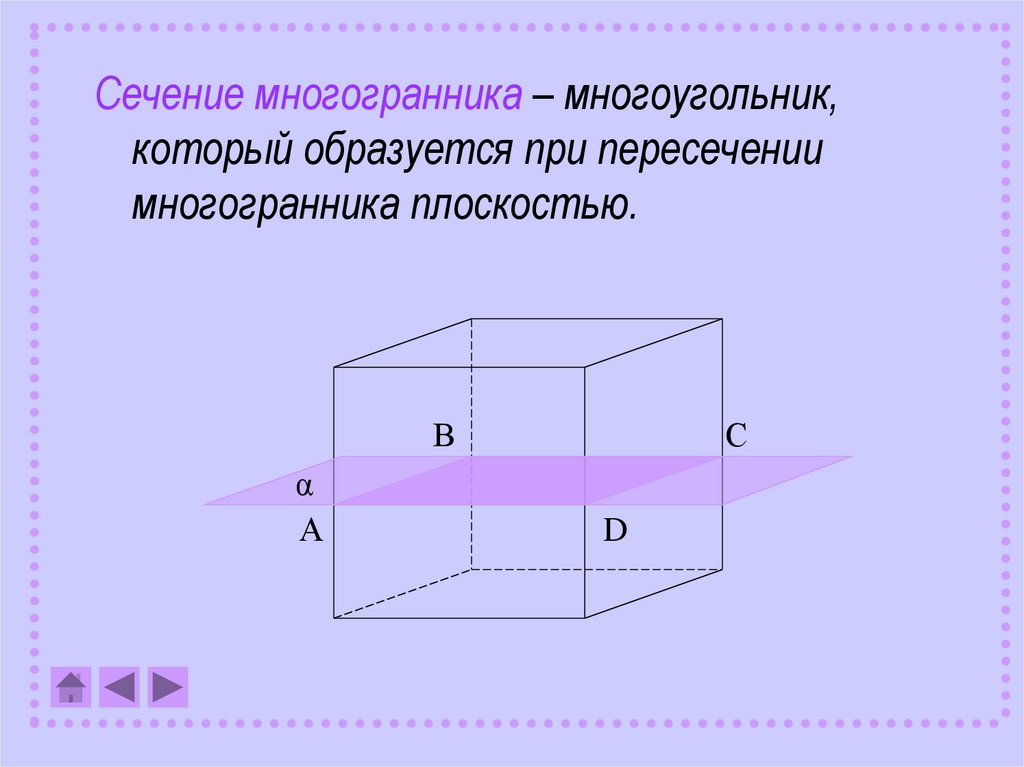
Сечение многогранника – многоугольник,который образуется при пересечении
многогранника плоскостью.
В
α
А
С
D
4.
Существует два основных способапостроения сечений:
1 Аксиоматический
2 Комбинированный
5.
Существует два основных способапостроения сечений:
1.1 Метод следов
1 Аксиоматический
1.2 Метод вспомогательных сечений
2 Комбинированный
6.
1 АксиоматическийСлед – это вспомогательная прямая,
являющаяся
изображением
лини
1.1 Метод
следов
секущей плоскости
с
1.2пересечения
Метод вспомогательных
сечений
плоскостью какой-либо грани
многогранника.
7.
В`` и QVC``
B``P
PC``
QR–-–след
следы
–- след
след
(PQR)
(PQR)
(PQR)
(PQR)на
на
на
на
B`A`C`
BB`
ACC`
ВАА`
и CC` сечение
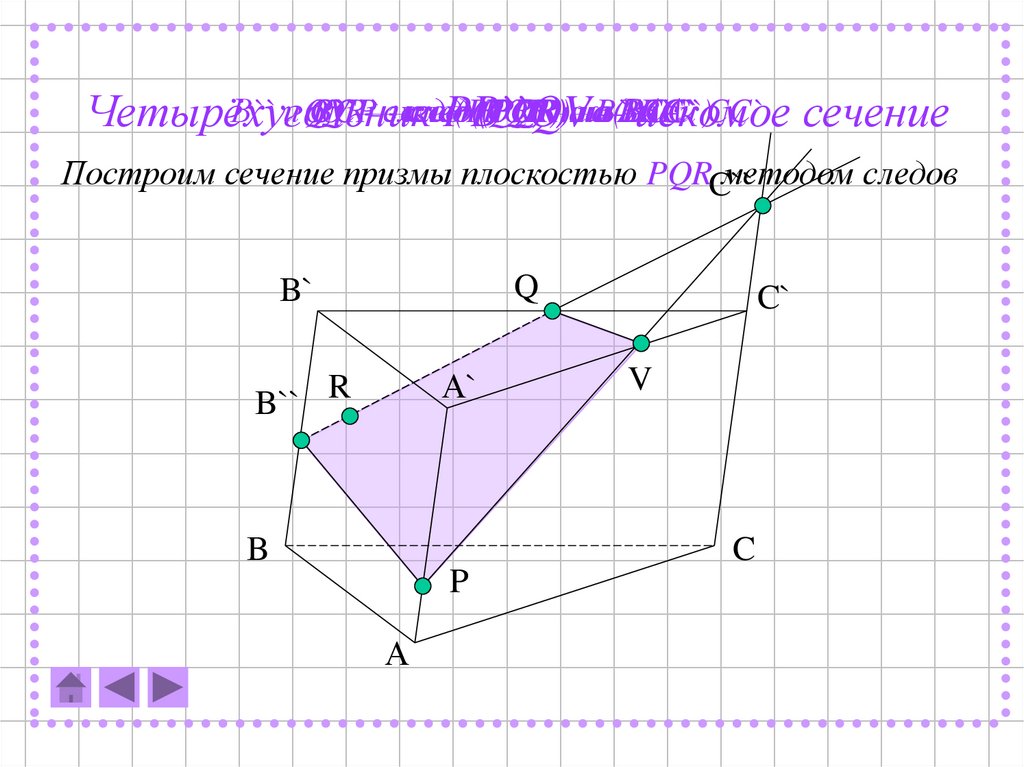
Четырёхугольник
PB``QV
–(BCC`)
искомое
Построим сечение призмы плоскостью PQRC``
методом следов
Q
B`
А`
B`` R
B
C`
V
C
P
А
8.
C``Многоугольник PS`S``QFPF –QF
след
S`P
след(PQR)на(B`A`C`)
(PQR)
––след
след
на(PQR)
(ACC`)
(PQR)на
на (ВАА`)
(BCC``)
SR
–-S``Q
основной
след
(PQR)
на (ABC)
искомое
сечение
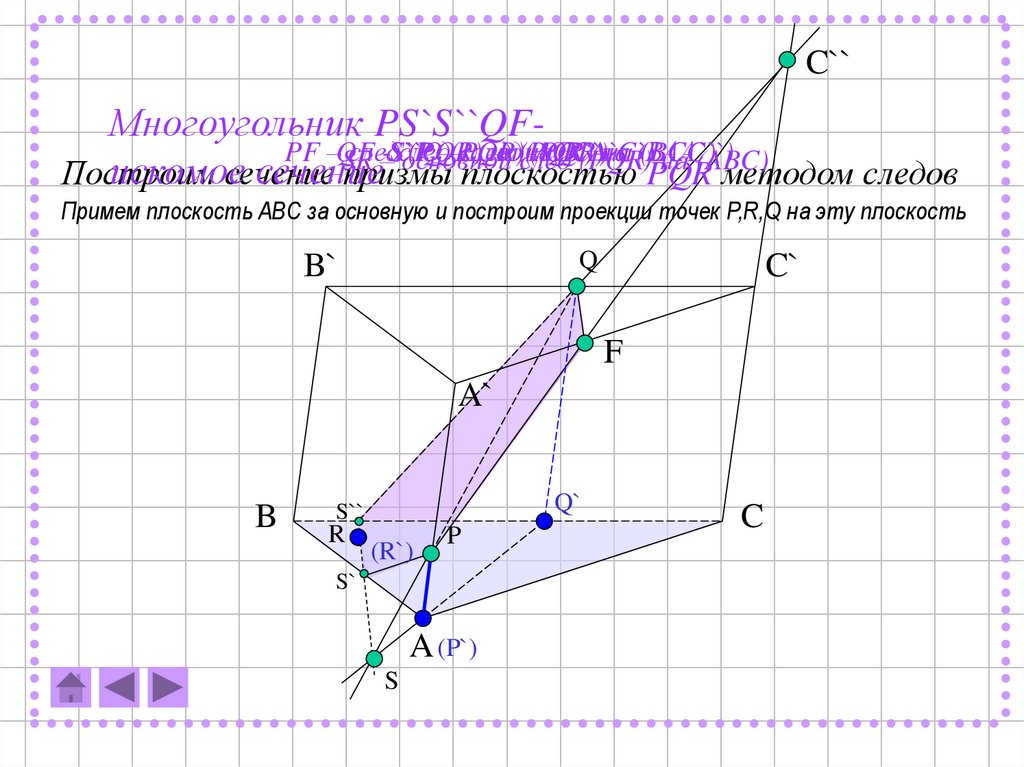
Построим
сечение
призмы плоскостью PQR
методом следов
Примем плоскость ABC за основную и построим проекции точек P,R,Q на эту плоскость
Q
B`
C`
F
A`
B
Q`
S``
R
(R`)
P
S`
A (P`)
S
C
9.
S`S``пирамиды- основной
след –плоскости
PQR
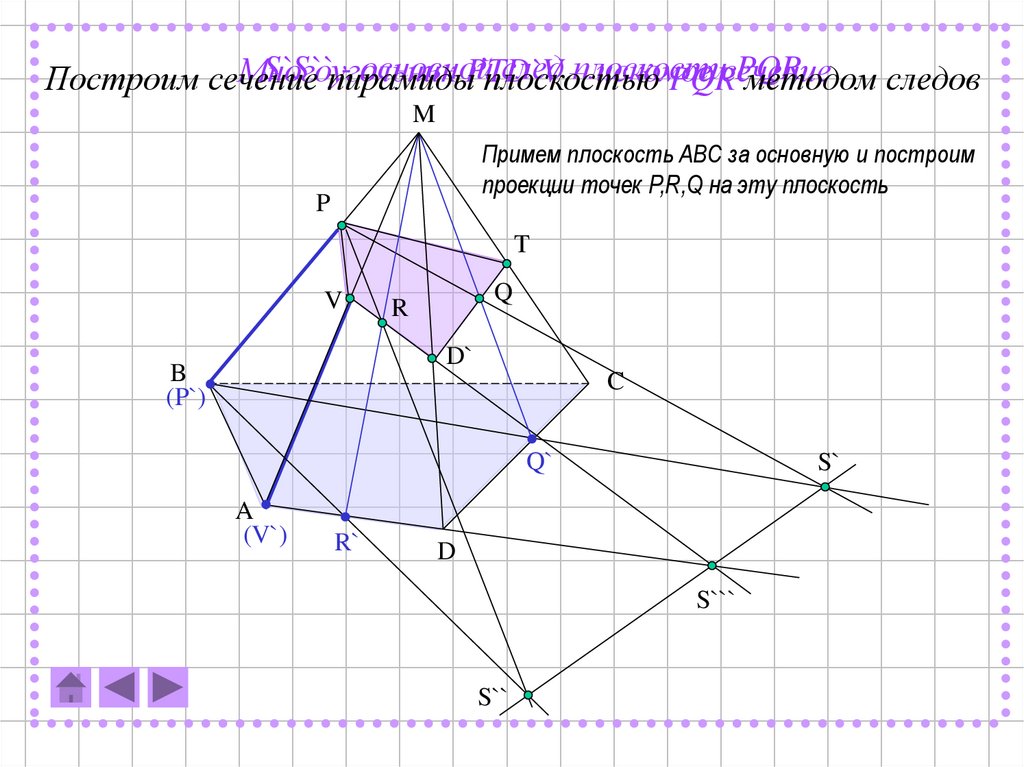
Многоугольник
PTD`V
искомое
Построим сечение
плоскостью
PQRсечение
методом следов
M
Примем плоскость ABC за основную и построим
проекции точек P,R,Q на эту плоскость
P
T
V
Q
R
D`
B
(P`)
C
Q`
A
(V`)
R`
S`
D
S```
S``
10.
1 АксиоматическийУниверсальный метод.
в тех случаях, когда,
1.1 Используется
Метод следов
нужный след секущей плоскости оказывается за
1.2 Метод вспомогательных сечений
пределами чертежа. Сущность метода заключается в
построении несложных вспомогательных сечений.
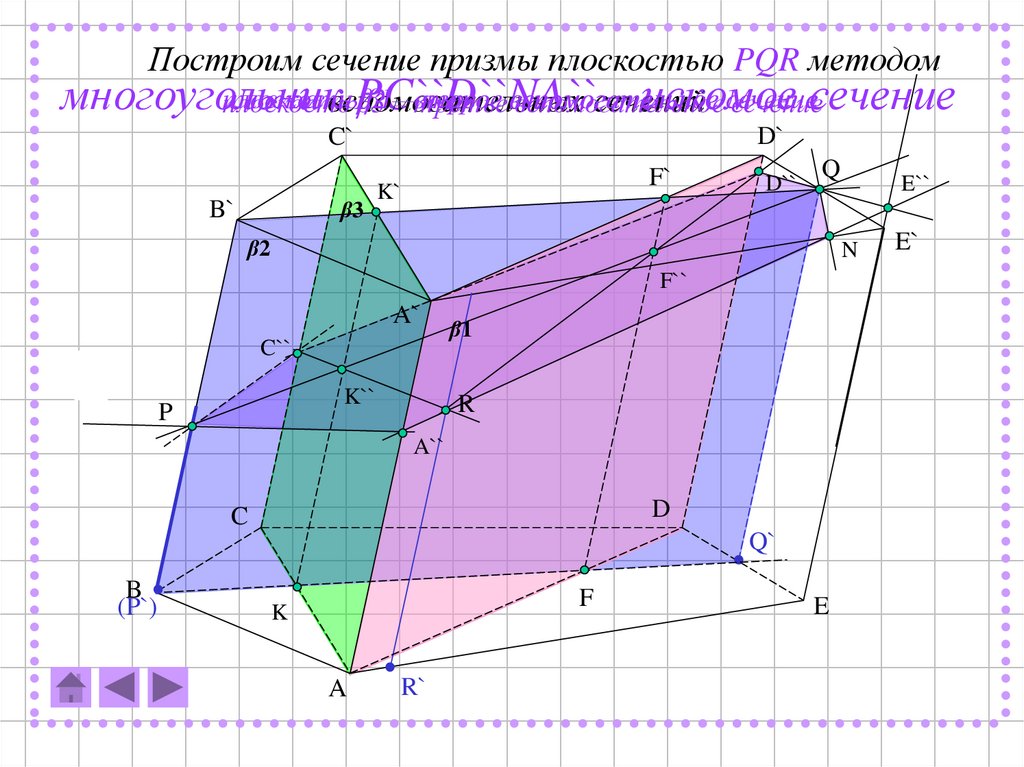
11.
Построим сечение призмы плоскостью PQR методомплоскость
плоскость
β2
β1––второе
первое вспомогательное
сечение
многоугольник
PC``D``NA``
– искомое
сечение
вспомогательных
сечений
β3
третье
вспомогательное
сечение
D`
C`
β3
B`
F`
K`
D``
Q
β2
N
F``
A`
C``
K``
P
β1
R
A``
D
C
Q`
B
(P`)
E``
F
K
A
R`
E
E`
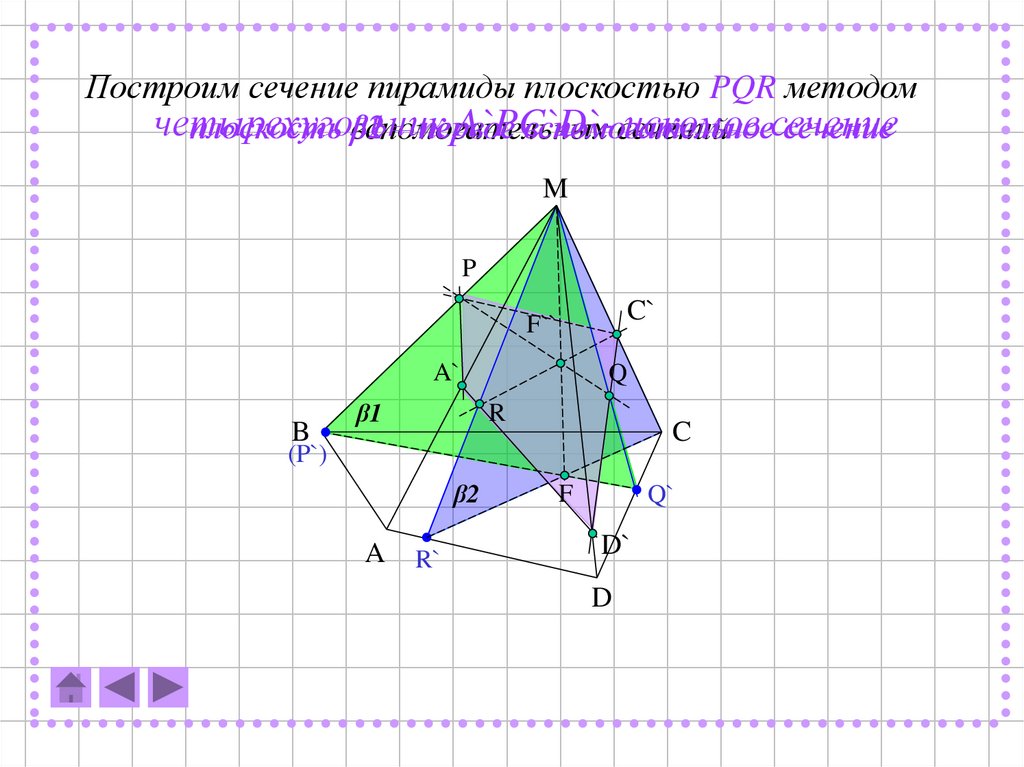
12.
Построим сечение пирамиды плоскостью PQR методомчетырехугольник
A`PC`D`искомое сечение
плоскость β2
β1 – первое
вспомогательное
сечение
вспомогательных
сечений
M
P
C`
F``
A`
B
β1
Q
R
C
(P`)
β2
A
R`
F
Q`
D`
D
13.
Существует два основных способапостроения сечений:
2.1 Построение сечения, проходящего через
заданную
прямую
параллельную другой
1
Аксиоматический
заданной прямой.
2 Комбинированный
2.2 Построение сечения, проходящего через
заданную точку параллельно двум заданным
Скрещивающимся прямым.
14.
2 Комбинированный2.1 Построение сечения, проходящего через
заданную прямую параллельную другой
заданной прямой.
2.2 Построение сечения, проходящего через
заданную точку параллельно двум заданным
Скрещивающимся прямым.
15.
Построимплоскостью
проходящей
через
1 Через
прямую q исечение
какую-нибудь
точку Wα,прямой
p проведем
плоскость
β
заданную
прямую
p параллельно второй заданной прямой q
2 В плоскости β через точку W проведём прямую q' параллельную q.
3 Пересекающимися прямыми p и q'. Определяется плоскость α,
плоскость искомого сечения
β
α
W
p
q`
q
16.
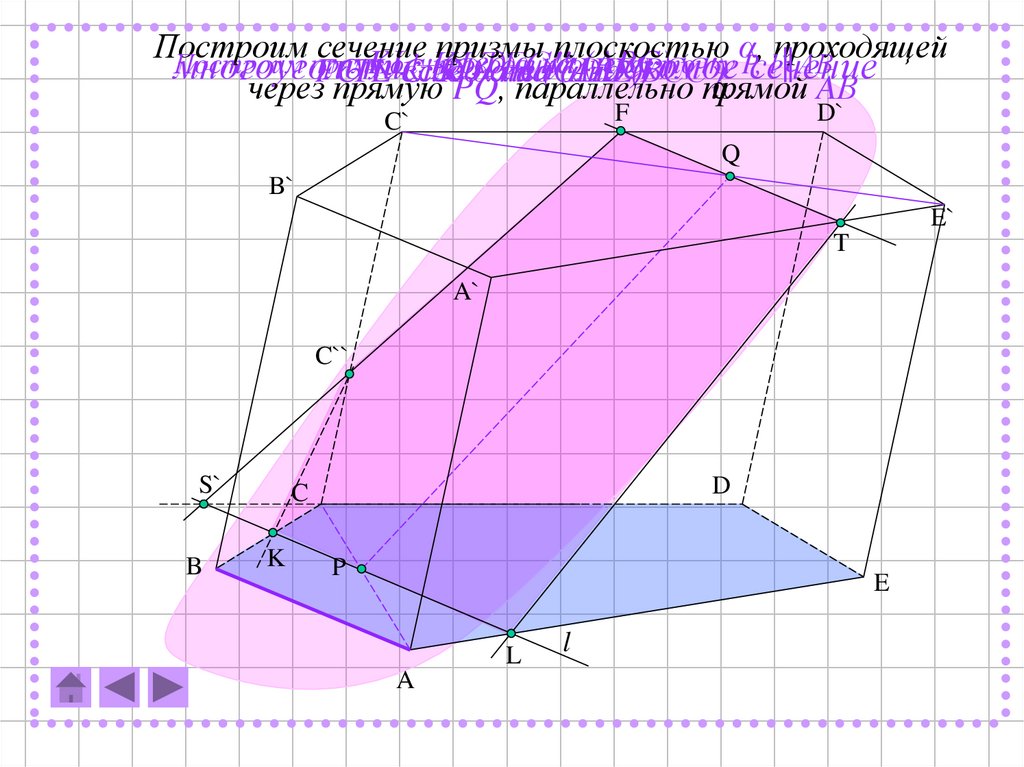
Построимсечение
призмы
плоскостью
α,
проходящей
Построим
прямую
KL
l,
–
проходящую
след
α
на
(ABC)
через
точку
P,
l║AB
многоугольник
KLTFC''
искомое
сечение
TL- -C''K
след
след
-αα
след
на
на(CDD')
(AEE')
α-на
(BCC')
α
черезFC''
прямую
PQ,
параллельно
прямой
AВ
F
C`
D`
Q
B`
E`
T
A`
C``
S`
B
D
C
K
P
E
L
A
l
17.
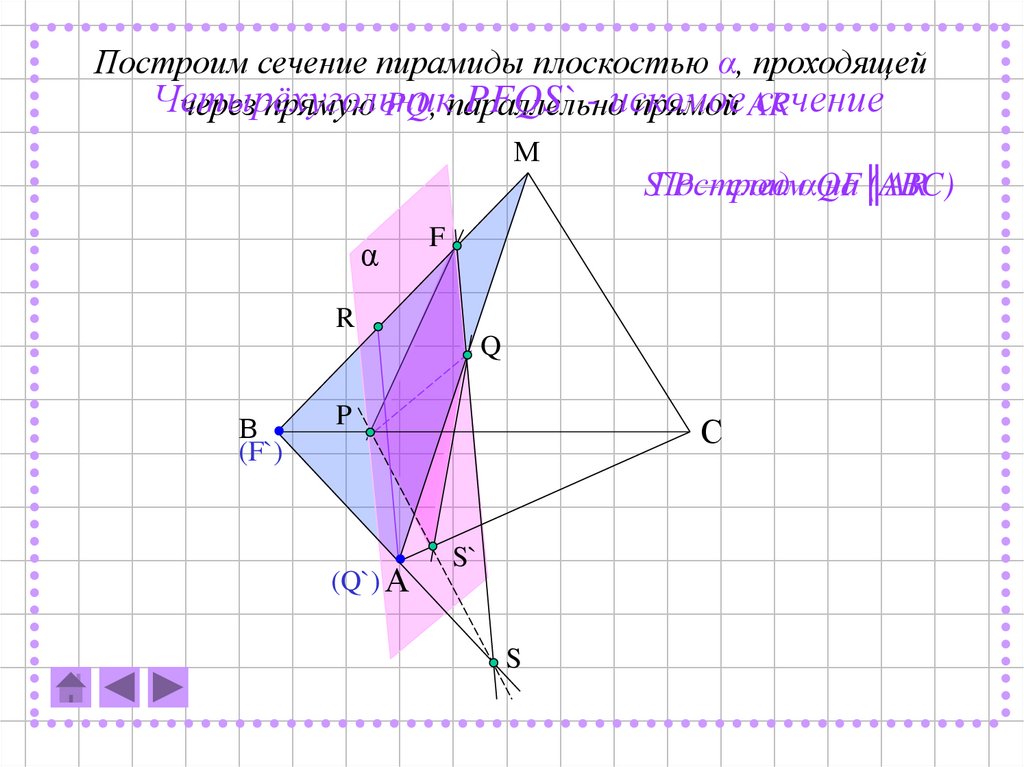
Построим сечение пирамиды плоскостью α, проходящейЧетырёхугольник
PFQS` - искомое
сечение
через прямую PQ, параллельно
прямой AR
М
α
S`P
Построим
– след αQF║AR
на (ABC)
F
R
Q
В
(F`)
P
(Q`) А
С
S`
S
18.
2 Комбинированный2.1 Построение сечения, проходящего через
заданную прямую параллельную другой
заданной прямой.
2.2 Построение сечения, проходящего через
заданную точку параллельно двум заданным
Скрещивающимся прямым.
19.
Построим сечение плоскостью α, проходящей через заданную точку К1 Выбираем некоторую точку W
параллельно 2-м заданным скрещивающимся прямым l и m
2 Проводим через неё прямые l` и m`параллельные прямым l и m
Прямыми l' и m' определяется
3 Строим
плоскость
сечение
β - плоскостью
плоскость вспомогательного
β.
сечения
4 Строим сечение плоскостью α, проходящей через точку K,
параллельно плоскости β.
l
β
K
m
m`
W
α
20.
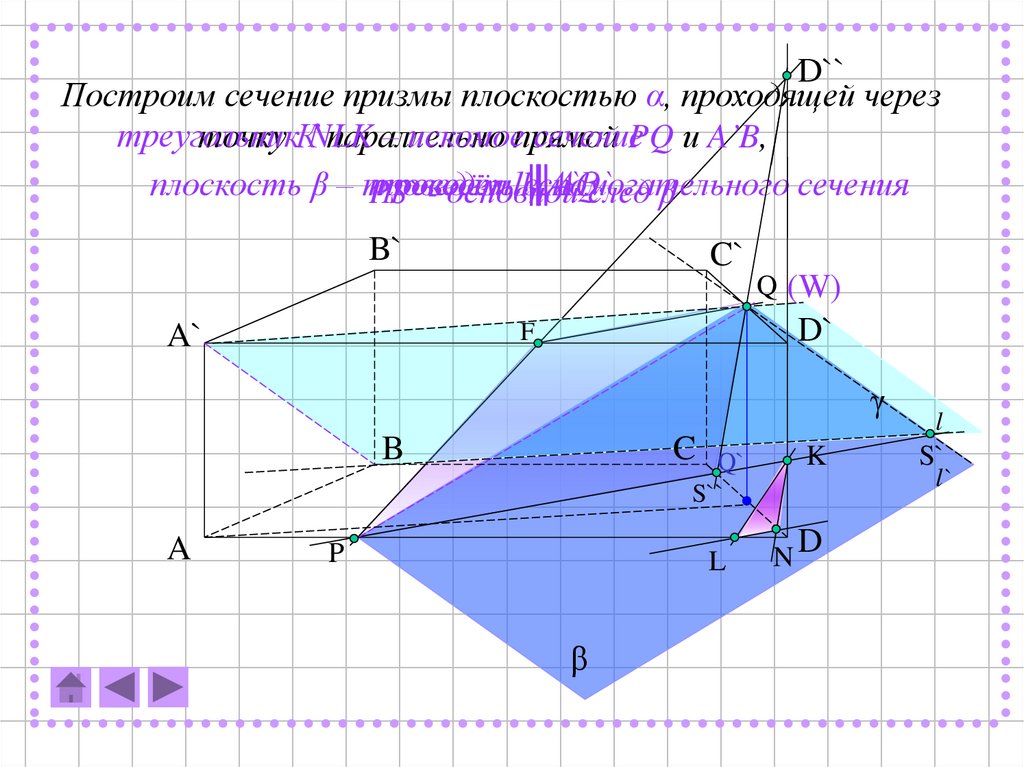
D``Построим сечение призмы плоскостью α, проходящей через
треугольник
– искомоепрямой
сечениеPQ и A’B,
точку КNLK
параллельно
плоскость β – плоскость
проведём
проведём
l║A`B
l║AQ`
вспомогательного
сечения
PS`
- основной
след β
B`
C`
Q (W)
D`
F
A`
γ
B
C Q`
K
S``
A
P
L
β
N
D
l
S`
l`
21.
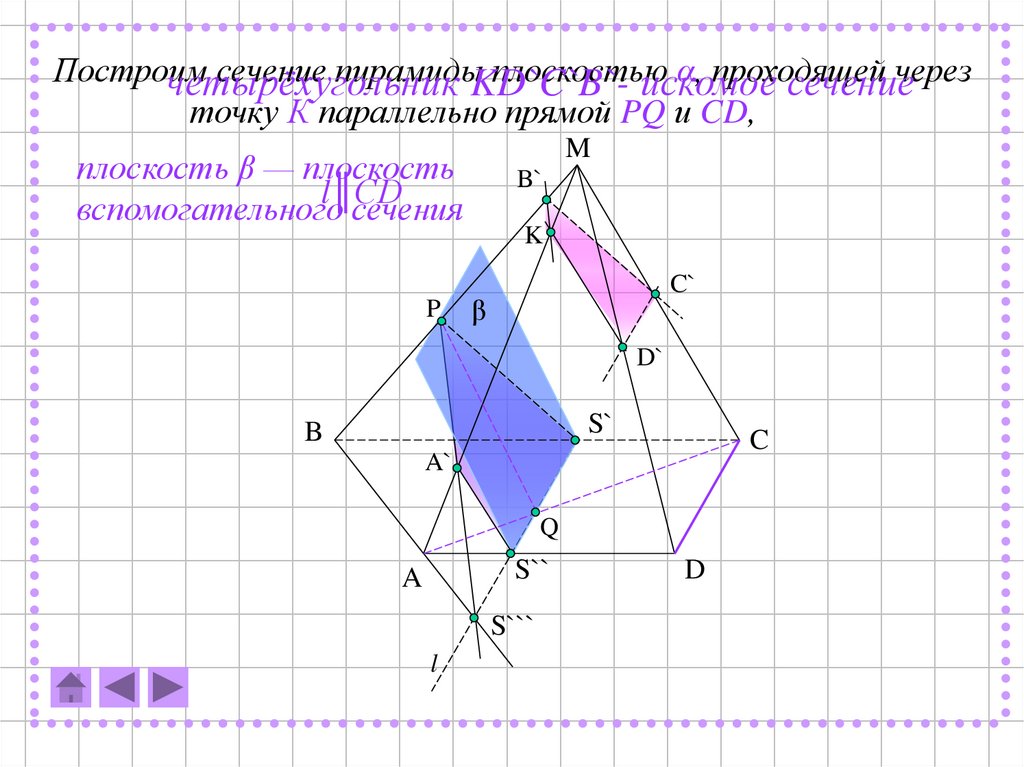
Построимсечение пирамидыKD`C`B`плоскостью
α, проходящей
через
четырёхугольник
искомое
сечение
точку К параллельно прямой PQ и CD,
M
плоскость β — плоскость
l║CD
вспомогательного
сечения
P
B`
K
C`
β
D`
S`
B
C
A`
Q
S``
A
S```
l
D
22.
Список используемой литературы1 Еженедельная учебно-методическая газета
«Математика» 31/2001. Объединение педагогических
изданий «Первое сентября».
2 В. Н. Литвиенко. Задачи на развитие
пространственных представлений, книга для учителя.
М.: Просвещение 1991 г.
3 Д. Е. Родионов, Е. М. Родионов. Стереометрия
в задачах. Пособие для поступающих в ВУЗы. М.:
Самсусам, 2002.
4 Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев,
Л. С. Киселёва, Э. Г. Позняк. Геометрия: учебник
для 10-11 классов средней школы.М.: Просвещение,












 Математика
Математика








