Похожие презентации:
Игровые модели. Примеры
1.
ИГРОВЫЕ МОДЕЛИ2.
Одной из неотъемлемых черт окружающего нас мираявляется присутствие (если не господство!) в нем
конфликтных ситуаций.
В расширительной трактовке под конфликтной ситуацией
мы понимаем такие ситуации, в которых сталкиваются
интересы двух (или более) сторон, преследующих разные
(иногда противоположные) цели, причем результаты
действия каждой из сторон зависят от того, как поведут
себя другие стороны.
3.
ПРИМЕРЫ (ВООБЩЕ):Боевые действия армий в военном конфликте
Выборы в парламент при наличии нескольких
кандидатов на одно место
Межвидовая борьба в природе
Разнообразные спортивные игры
и др.
4.
ПРИМЕРЫ В ЭКОНОМИКЕ:борьба фирм за рынки сбыта
явления олигополии
планирование рекламных компаний
формирование цен на конкурентных рынках
биржевая игра
и др.
5.
ЗАДАЧА:провести научный анализ обобщенной конфликтной
ситуации и попытаться выработать разумные
правила поведения для ее участников.
Именно этим и занимается теория игр математическая теория конфликтных ситуаций.
В ней под игрой понимается математическая модель
конфликтной ситуации
6.
Теория игр впервые была систематическиизложена Дж. фон Нейманом и О. Моргенштерном
в 1944 году в книге «Теория игр и экономическое
поведение»
7.
ОСНОВНЫЕ СОСТАВЛЯЮЩИЕЛЮБОЙ ИГРЫ
1) Множество конфликтующих сторон (игроков):
I={P1, P2,…,Pn}
2) Cовокупности множеств стратегий каждого из игроков
{Si}iєI
3) Cовокупности функций выигрыша каждого из игроков
{Hi}iєI
8.
ПОЯСНЕНИЯ:Стратегия игрока - одна из возможных линий
поведения в течение одной партии (однократном
осуществлении игры)
Ситуация – набор стратегий всех игроков
Выигрыш игрока - степень удовлетворения его
интересов в данной ситуации
9.
ПРЕДПОЛАГАЕТСЯ:Функции выигрыша и множества стратегий игроков
общеизвестны.
В соответствии с этой информацией каждый из
участников игры и организует свое поведение,
стремясь обеспечить себе максимально возможный
выигрыш при любых действиях партнеров
10.
Содержательный анализ игры в такой обобщеннойпостановке весьма затруднителен.
Методы анализа игр значительно различаются в
зависимости от числа игроков, от количества
стратегий, от свойств платежных функций, а также от
характера предварительной договоренности между
игроками.
11.
Наиболее изученный класс игр - классматричных игр
12.
ОПИСАНИЕ МАТРИЧНОЙ ИГРЫВ игре участвуют 2 игрока: А и В
Каждый из игроков располагает конечным набором стратегий:
А1,…,Аm и В1,…,Вn - возможные стратегии игроков А и В
(Аi,Bj) – возможные ситуации в игре
Значения функций выигрыша НА и НВ игроков в каждой ситуации
равны по величине и противоположны по знаку, то есть
НА(Аi,Bj)=-HB(Ai,Bj)= aij
(выигрыш одного из игроков равен проигрышу другого)
(антагонизм!)
13.
ОЧЕВИДНОзадание матричной игры эквивалентно заданию всех
значений функции выигрыша одного из игроков
(например, игрока А) в виде так называемой платежной
матрицы или матрицы игры:
a11
a 21
H
...
a m1
a12
a 22
...
am2
... a1n
... a 2 n
... ...
... a m n
14.
В ЭТОЙ МАТРИЦЕ:Строки – стратегии игрока А
Столбцы – стратегии игрока В
Элементы aij - выигрыши игрока А в ситуации, когда А
выбирает стратегию Аi, а В – стратегию Вj
15.
ПРИМЕР:Каждый из двух игроков А и В независимо друг от
друга кладет на стол монету в 1 рубль или в 2 рубля.
Если монеты одинаковые, то выигрывает игрок А,
если разные - игрок В. Выигрыш равен сумме
достоинств монет. Необходимо построить
платежную матрицу игры
16.
ОТВЕТ:17.
Окончательная цель теории игр состоит вопределении для каждого игрока стратегий,
удовлетворяющих некоторым условиям
оптимальности.
Это и называется решением игры.
18.
ТОНКОСТЬ:для многих естественных классов игр выбор
удовлетворительного принципа оптимальности
весьма затруднителен, не говоря уже о поиске
оптимальных стратегий игроков
19.
Для матричных игр основной принцип оптимальности– принцип минимакса:
«поступайте так, чтобы при наихудшем для вас
поведении противника получить максимальный
выигрыш»
или:
«выбирайте наилучшее из наихудшего»
20.
РЕАЛИЗАЦИЯ ПРИНЦИПА МИНИМАКСАДля игрока А:
- в каждой строке находим минимальный элемент;
- из этих минимальных элементов выбираем максимальный
α=maxi minj aij
Для игрока В:
- в каждом столбце находим максимальный элемент;
- из этих максимальных элементов выбираем минимальный
β=minj maxi aij
21.
α - нижняя цена игры, или максимин.Это гарантированный выигрыш игрока А при любой стратегии
игрока В.
Стратегия, соответствующая максимину, называется
максиминной стратегией (их может быть несколько).
β - верхняя цена игры, или минимакс.
Это - гарантированный проигрыш игрока В (β с обратным
знаком - гарантированный выигрыш игрока В).
Стратегия, соответствующая минимаксу, называется
минимаксной стратегией
22.
ВОПРОС:Можно ли считать таким образом
найденные максиминные и
минимаксные стратегии игроков
безусловно оптимальными для них?
23.
Имеются две принципиальноразличные ситуации:
1) α=β
2) α<β
24.
ПРИМЕР 125.
1 СИТУАЦИЯ:α=β=v
общее значение v называют ценой игры,
соответствующие стратегии - оптимальными чистыми стратегиями,
их совокупность - решением.
При этом решение игры обладает очень важным свойством
устойчивости: если один из игроков придерживается своей
оптимальной стратегии, то для другого игрока не может
быть выгодным отклоняться от своей оптимальной
стратегии.
(седловая точка!)
26.
ПРИМЕР 227.
2 СИТУАЦИЯα<β
Пара, состоящая из максиминной и минимаксной стратегий
игроков, вряд ли может считаться вполне оптимальной для
них, т.к. не выполняется условие устойчивости
Как быть?
28.
СМЕШАННОЕ РАСШИРЕНИЕ ИГРЫПусть матричная антагонистическая игра двух игроков А и В задана
платежной матрицей
a11 a12 ... a1n
a 21 a 22 ... a 2 n
H
... ... ... ...
a m1 a m 2 ... a m n
Предположим также, что игра состоит из большого числа партий.
Поэтому, стремясь к максимизации суммарного выигрыша, каждый игрок
может свои стратегии «смешивать», чередуя с какой-либо частотой.
29.
СМЕШАННЫЕ СТРАТЕГИИСмешанной стратегией игрока А назовем неотрицательный вектор вида:
SA=(p1,p2,…, pm),
где pi - вероятность применения игроком А стратегии Ai,
причем р1+р2+…+pm=1
Смешанной стратегией игрока В назовем неотрицательный вектор вида:
SВ=(q1, q2,…, qn),
где qj - вероятность применения игроком А стратегии Ai,
причем q1+q2+…+qn=1
30.
Пусть игроки А и В независимо друг от друга выбралисоответственно стратегии SA и SB.
Тогда средний выигрыш игрока А составит:
HA(SA,SB)=∑i∑j aij*pi*qj
Cредний выигрыш игрока B:
HB(SA,SB)= -HA(SA,SB)
Руководствуясь принципом минимакса, каждый игрок
стремится в наибольшей степени увеличить свой
гарантированный средний выигрыш.
31.
ПОЛУЧАЕМαS=maxSA minSB HA(SA,SB) - значение гарантированного
среднего выигрыша игрока А в одной партии (аналог
нижней цены игры в случае чистых стратегий)
βS=minSB maxSF HA(SA,SB) - значение гарантированного
среднего проигрыша игрока В в одной партии (аналог
верхней цены игры в случае чистых стратегий)
32.
ОСНОВНОЙ РЕЗУЛЬТАТ ТЕОРИИМАТРИЧНЫХ ИГР (ТЕОРЕМА ФОН
НЕЙМАНА)
Для матричной игры с любой платежной матрицей Н
величины αS и βS существуют и равны между собой.
Более того, существует хотя бы одна пара смешанных
стратегий SA* и SB*, для которых выполняется:
Н(SA*,SB*)= αS = βS .
33.
Стратегии SA* и SB* называются оптимальнымисмешанными стратегиями;
пара таких стратегий – решением игры в
смешанных стратегиях,
а общее значение vS для αS и βS - ценой такой
игры.
Если vS=0, то игра называется справедливой
34.
Как и в случае игры с седловой точкой, решение игрыв смешанных стратегиях является устойчивым:
если один из игроков придерживается своей
оптимальной смешанной стратегии, то другому не
может быть выгодно отступление от своей
оптимальной стратегии
35.
СВОЙСТВО 1Игры, заданные платежными матрицами
одинаковой размерности, элементы которых
связаны линейным соотношением имеют
одинаковые решения в смешанных стратегиях.
Цены таких игр связаны тем же соотношением
36.
СВОЙСТВО 2Для любой матричной игры справедливо
двойное неравенство:
α≤vS≤β
37.
МЕТОДЫ РЕШЕНИЯ МАТРИЧНЫХ ИГР.МЕТОД 1. ИГРЫ 2Х2
a11 a12
.
H
a 21 a 22
р1=(а22–а21)/(а11+а22–а12–а21),
р2=1–р1
q1=(a22–a12)/(a11+a22–a12–a21),
q2=1–q1
vS=(a22·a11-a12·a21)/(a11+a22–a12–a21)
38.
ПРИМЕРНайти оптимальные смешанные стратегии
игроков в игре про монеты. Справедлива ли эта
игра?
39.
МЕТОД 2. УПРОЩЕНИЕ ИГР С ПОМОЩЬЮОТБРАСЫВАНИЯ ДОМИНИРУЕМЫХ
СТРАТЕГИЙ
Стратегия Аi игрока А называется доминирующей над
стратегией Аk (а стратегия Аk доминируемой стратегией Аi),
если все элементы i-й строки платежной матрицы не меньше
соответствующих элементов k-й строки
Стратегия Вj игрока В называется доминирующей над
стратегией Вl (а стратегия Вl - доминируемой стратегией Вj),
если все элементы j-го столбца платежной матрицы не
больше соответствующих элементов l-го столбца
40.
Доминируемая стратегия является заведомоневыгодной для игрока, ее выбирающего, и потому
при дальнейшем исследовании игры может быть
отброшена.
41.
ПРИМЕР:42.
МЕТОД 3. ГРАФИЧЕСКИЙ МЕТОДПрименяется для решения игр 2хn и mx2
43.
МЕТОД 4. СВЕДЕНИЕ ИГРЫ К ЗАДАЧЕЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Задача ЛП для игрока А
Найти неотрицательные значения x1, x2,…, xm, которые удовлетворяют
линейным ограничениям – неравенствам
и обращают в минимум целевую функцию L=x1+x2+…+xm
44.
Задача ЛП для игрока ВНайти неотрицательные значения у1, у2,…, уn, которые удовлетворяют
линейным ограничениям – неравенствам
и обращают в максимум целевую функцию L=у1+у2+…+уn
45.
Пусть (x1*,x2*,…,xm*) - некоторое решение первой задачи,L* - минимальное значение целевой функции.
Тогда цена игры vS=1/L*, а компоненты оптимальной
стратегии игрока А равны: pj*=xj*/L*
Пусть (у1*,у2*,…,уn*) - некоторое решение второй задачи,
L* - максимальное значение целевой функции .
Тогда цена игры vS=1/L*, а компоненты оптимальной
стратегии игрока В равны: qi*=yi*/L*
46.
ВАЖНОЕ ДОПОЛНЕНИЕФормулы справедливы только, когда цена игры >0.
Если это не так, то предварительно необходимо
преобразовать исходную матрицу, прибавив, например, ко
всем элементам модуль наименьшего отрицательного
элемента.
47.
МЕТОД 5. МЕТОД БРАУНАРОБИНСОНОсновная идея:
Разыгрывается «мысленный» эксперимент, в котором игроки А и В
поочередно применяют друг против друга свои стратегии, стремясь
выиграть побольше.
При этом каждый игрок при выборе очередной стратегии ориентируется
не на оптимальный выигрыш относительно последней стратегии
противника, а на оптимальный «накопленный» выигрыш за все
предыдущие ходы.
Приближенные оптимальные стратегии игроков определяются
относительными частотами применения ими чистых стратегий.
48.
ПРИМЕР:Найти приближенное решение игры, заданной матрицей
49.
РЕАЛИЗАЦИЯ МЕТОДАk
Ai
B1
B2
B3
Bj
A1
A2
A3
v*
v*
vS
1
2
3
4
5
6
7
8
9
10
11
12
1
A3
7
5
4*
B3
8*
2
4
4.00
8.00
6.00
2
A1
10*
11
12
B1
11*
11
11
5.00
5.50
5.25
3
A1
13*
17
20
B1
14
20*
18
4.33
6.67
5.55
4
A2
22
21*
22
B2
20
24*
23
5.25
6.00
5.63
5
A2
31
25
24*
B3
28*
26
27
4.80
5.60
5.20
6
A1
34
31*
32
B2
34*
30
32
5.17
5.67
5.32
7
A1
37*
37
40
B1
37
39*
39
5.29
5.86
5.58
8
A2
46
41*
42
B2
43
43
44*
5.13
5.50
5.31
9
A3
53
46*
46
B2
49*
47
49
5.11
5.37
5.24
10
A1
56
52*
54
B2
55*
51
54
5.20
5.50
5.35
…
…
…
…
…
…
…
…
…
…
…
…
50.
ОТВЕТ:SA≈(0.5, 0.3, 0.2), SB≈(0.3, 0.5, 0.2), VS≈5,35
Для сравнения точное решение:
SA*=(0.4, 0, 0.6), SB*=(0.2, 0.8, 0), vS=5.4
51.
ДВА ВЫВОДА О МЕТОДЕ БРАУНА1) Метод Брауна позволяет сравнительно просто
находить приближенные решения матричных игр,
причем трудоемкость метода с увеличением
размерности игры возрастает незначительно
2) Сходимость приближенных решений,
рассчитанных методом Брауна, к точному решению
происходит довольно медленно















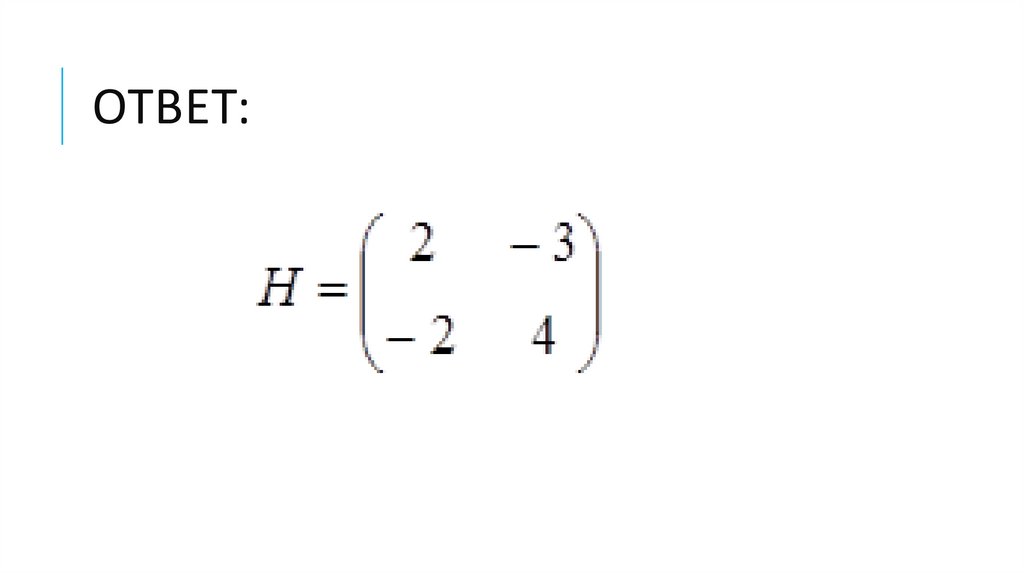



































 Математика
Математика








