Похожие презентации:
Теория игр. Введение в матричные игры
1.
Теория игрЛекция 1-2
Введение в матричные игры
2. Введение в матричные игры
1.2.
3.
4.
История предмета теории игр
Представление игры
Классификация игр
Решение матричных игр в чистых
стратегиях
5. Смешанные стратегии
6. Методы решения матричных игр
3. Изучение курса теории игр
4. История предмета теории игр
• Теория игр является частью теории принятиярешений. В теории принятия решений у лица,
принимающего решения (ЛПР), имеется ряд
альтернатив и его целью является выбор наилучшей
альтернативы, принятие оптимального решения.
• Различают задачу оптимизации –принятие
оптимального решения одним ЛПР в
бесконфликтной ситуации – и задачу теории игр,
занимающуюся отысканием оптимальных решений
для нескольких ЛПР( игроков), в рамках их
конфликтного взаимодействия, обусловленного
несовпадением их интересов.
16.10.2018
4
5. История предмета теории игр
• Теория игр — математический метод изученияоптимальных стратегий в играх.
• Теория игр – это совокупность математических методов
анализа и оценки конфликтных ситуаций.
• Под игрой понимается процесс, в котором участвуют две
и более сторон, ведущих борьбу за реализацию своих
интересов. Каждая из сторон имеет свою цель и
использует некоторую стратегию, которая может вести к
выигрышу или проигрышу — в зависимости от поведения
других игроков.
• Теория игр изучает ситуации принятия решений
несколькими взаимодействующими игроками.
• Теория игр помогает выбрать лучшие стратегии с учётом
представлений о других участниках, их ресурсах и их
возможных поступках.
16.10.2018
5
6. История предмета теории игр
• Содержание теории игр:1. установление принципов оптимального
поведения в условиях неопределенности
(конфликта),
2. доказательство существования решений,
удовлетворяющих этим принципам,
3. указание алгоритмов нахождения решений, их
реализация.
• Моделями теории игр можно описать
биологические, экономические, правовые,
классовые, военные конфликты,
взаимодействие человека с природой.
• Все такие модели в теории игр принято называть
играми.
16.10.2018
6
7. История предмета теории игр
• Оптимальные решения или стратегии в математическоммоделировании предлагались ещё в XVIII в. Задачи
производства и ценообразования в условиях
олигополии, которые стали позже хрестоматийными
примерами теории игр, рассматривались в XIX в. А. Курно
и Ж.Бертраном. В начале XX в. Э.Ласкер, Э.Цермело,
Э.Борель выдвигают идею математической теории
конфликта интересов.
• Математическая теория игр берёт своё начало из
неоклассической экономики. Впервые математические
аспекты и приложения теории были изложены в
классической книге 1944 года Джона фон Неймана и
Оскара Моргенштерна «Теория игр и экономическое
поведение»
16.10.2018
7
8. История предмета теории игр
• Дж. Нэш в 1949 году пишет диссертацию по теорииигр, через 45 лет он получает Нобелевскую премию
по экономике. В Принстонском университете
Дж.Нэш посещал лекции Дж. Неймана. В своих
трудах Дж. Нэш разработал принципы
«управленческой динамики». Первые концепции
теории игр анализировали антагонистические
игры, когда есть проигравшие и выигравшие за
их счет игроки. Нэш разрабатывает методы анализа,
в которых все участники или выигрывают, или
терпят поражение. Эти ситуации получили
названия «равновесие по Нэшу», или
«некооперативное равновесие».
16.10.2018
8
9. История предмета теории игр
• Игрокам выгодно сохранять это равновесие, таккак любое изменение ухудшит их положение.
Эти работы Дж. Нэша сделали серьёзный вклад
в развитие теории игр, были пересмотрены
математические инструменты экономического
моделирования. Дж. Нэш показывает, что
классический подход к конкуренции А.Смита,
когда каждый сам за себя, не оптимален. Более
оптимальны стратегии, когда каждый
старается сделать лучше для себя, делая
лучше для других.
16.10.2018
9
10. История предмета теории игр
• Хотя теория игр первоначально и рассматривалаэкономические модели, вплоть до 1950-х она
оставалась формальной теорией в рамках
математики. С 1950-х гг. начинаются попытки
применить методы теории игр не только в
экономике, но в биологии, кибернетике, технике,
антропологии и военной области.
• С середины 1980-х гг. начинается активное
практическое использование теории игр, особенно
в экономике и менеджменте. За последние 20 —
30 лет значение теории игр и интерес значительно
растет, некоторые направления современной
экономической теории невозможно изложить без
применения теории игр.
16.10.2018
10
11. История предмета теории игр
• Большим вкладом в применение теории игр сталаработа Томаса Шеллинга, нобелевского лауреата
по экономике 2005 г. «Стратегия конфликта».
• Игры также используются для обучения в бизнескейсах, семинарах Г. П. Щедровицкого,
основоположника организационно-деятельностного
подхода. Понятие игры используется в психологии
и культурологии.
• Математическая теория игр сейчас бурно
развивается, рассматриваются динамические игры.
16.10.2018
11
12. История предмета теории игр
• Нобелевскими лауреатами по экономике задостижения в области теории игр и экономической
теории стали: Роберт Ауманн, Райнхард Зелтен,
Джон Нэш, Джон Харсаньи, Уильям Викри, Джеймс
Миррлис, Томас Шеллинг, Джордж Акерлоф, Майкл
Спенс, Джозеф Стиглиц, Леонид Гурвиц, Эрик
Мэскин, Роджер Майерсон.
• Однако, математический аппарат теории игр —
затратен. Его применяют для оправданных задач:
политика, экономика монополий и распределения
рыночной власти и т. п.
16.10.2018
12
13. История предмета теории игр
• Лауреатами Нобелевской премии в экономикеза 2012 стали Элвин Рот из Гарварда, США, и
Ллойд Шепли из Калифорнийского
университета, США за цикл работ - «Теория
устойчивых распределений и практика
рыночного конструирования». Весь механизм
базируется на алгоритме Гейла — Шепли,
разработанном в 1962 году Ллойдом Шепли и
Дэвидом Гейлом.
• Лауреатами Нобелевской премии в экономике
за 2014 стал Жан Тироль (Анализ рыночной
власти и её регулирования)
16.10.2018
13
14. Представление игры
• Игры представляют собой строгоопределённые математические объекты.
• Игра образуется игроками, набором стратегий
для каждого игрока и указания выигрышей, или
платежей, игроков для каждой комбинации
стратегий.
• Большинство кооперативных игр описываются
характеристической функцией, в то время как
для остальных видов чаще используют
нормальную или экстенсивную форму.
16.10.2018
14
15. Представление игры
• Характеризующие признаки игры какматематической модели ситуации:
1. наличие нескольких участников;
2. неопределенность поведения участников,
связанная с наличием у каждого из них нескольких
вариантов действий;
3. различие (несовпадение) интересов участников;
4. взаимосвязанность поведения участников,
поскольку результат, получаемый каждым из них,
зависит от поведения всех участников;
5. наличие правил поведения, известных всем
участникам.
16.10.2018
15
16. Представление игры
• Определение:Игра – математическая модель конфликтной
ситуации.
• Определение:
Ход в игре – выбор и осуществление игроком
одного из предусмотренных правилами игры
действий.
• Определение:
Стратегия – последовательность всех ходов до
окончания игры.
16.10.2018
16
17. Представление игры
• Анализ конфликтной ситуации начинаетсяс построения формальной модели, т.е.
превращения ее в игру.
• Существует несколько способов
представления игры:
1. Развернутая( экстенсивная, или
позиционная) форма;
2. Стратегическая (нормальная) форма;
3. Байесова форма.
16.10.2018
17
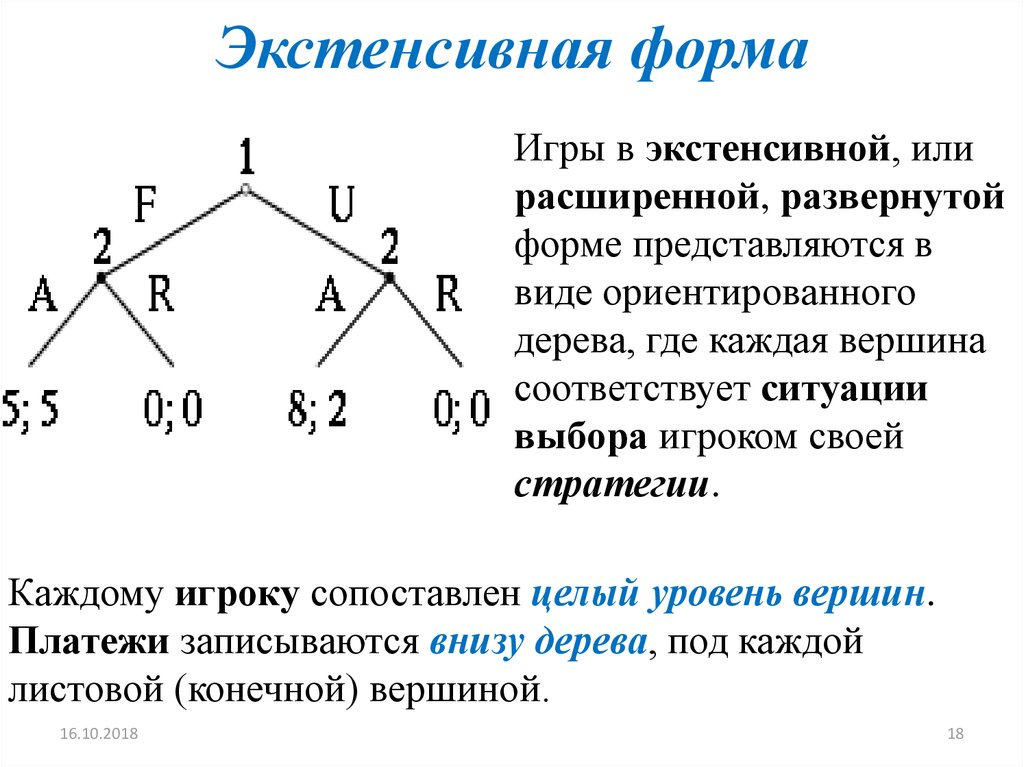
18. Экстенсивная форма
Игры в экстенсивной, илирасширенной, развернутой
форме представляются в
виде ориентированного
дерева, где каждая вершина
соответствует ситуации
выбора игроком своей
стратегии.
Каждому игроку сопоставлен целый уровень вершин.
Платежи записываются внизу дерева, под каждой
листовой (конечной) вершиной.
16.10.2018
18
19. Нормальная форма
• В нормальной, или стратегической, форме играописывается платёжной матрицей. Каждая
сторона (точнее, измерение) матрицы — это игрок,
строки определяют стратегии первого игрока, а
столбцы — второго. На пересечении двух
стратегий можно увидеть выигрыши, которые
получат игроки.
• В примере , если игрок 1 выбирает первую
стратегию, а второй игрок — вторую стратегию, то
на пересечении мы видим (−1, −1), это значит, что в
результате хода оба игрока потеряли по одному очку.
16.10.2018
19
20. Нормальная форма
Игрок 2стратегия 1
Игрок 1
стратегия 1
Игрок 1
стратегия 2
4, 3
0, 0
Игрок 2
стратегия 2
–1, –1
3, 4
Нормальная форма для игры с 2 игроками, у
каждого из которых по 2 стратегии.
16.10.2018
20
21. 2. Классификация игр
• Игры можно классифицировать по различнымпризнакам:
1. стратегические и чисто случайные,
2. бескоалиционные и коалиционные,
3. игры 1, 2, …, n лиц (по числу игроков),
4. конечные и бесконечные (по числу стратегий),
5. игры в нормальной форме и динамические,
6. с нулевой суммой («антагонистические») и с
ненулевой суммой.
7. Статические и динамические игры.
8. Игры с полной и неполной информацией.
9. Игры с совершенной и несовершенной
информацией.
10. Метаигры.
16.10.2018
21
22. 2. Классификация игр
• Определение:В играх с нулевой суммой одни игроки
выигрывают за счет других, т.е. суммарный
выигрыш всех игроков равен нулю.
• Определение:
Парные игры с нулевой суммой называются
антагонистическими.
• Определение:
Конечные антагонистические игры
называются матричными играми.
16.10.2018
22
23. Решение матричных игр в чистых стратегиях
• Рассмотрим простейшую модель – игру, в которойучаствуют два игрока (парная), множество
стратегий каждого игрока конечно (конечная), а
выигрыш одного игрока равен проигрышу другого
(бескоалиционная, конечная, антагонистическая
парная игра ). Такую игру (Г) называют матричной.
Она определяется тройкой Г=(X,Y,K), где Х –
множество стратегий 1-го игрока, Y – множество
стратегий 2-го игрока, K=K(x,y) – функция
выигрыша (выигрыш 1-го игрока и соответственно
проигрыш 2-го при условии, что 1-й игрок выбрал
стратегию x , а 2-й – стратегию y). Пару (x,y)
называют ситуацией в игре Г.
16.10.2018
23
24. Решение матричных игр в чистых стратегиях
1. Пусть игрок Р1 располагает m стратегиями (a 1, …,a i, …, a m ) , а игрок Р2 располагает n стратегиями
(a 1, …, a j, …, a n).
2. Выбор игроком Р1 стратегии a i (строки a i матрицы
A) и выбор игроком Р2 стратегии a j (столбца a j
матрицы A) приводит к тому, что игрок Р1
выигрывает некоторую величину a ij ( a ij >0), а
игрок Р2 ее проигрывает. Стратегии называются
чистыми. Далее везде для игрока Р1 используем
термин выигрыш, а для игрока Р2 проигрыш.
3. Тогда игра Г полностью определяется заданием
матрицы A. Матрица А = ( a ij ) mn называется
матрицей игры или платежной матрицей.
16.10.2018
24
25. Платежная матрица
Стратегии игрока Р2a1
…
aj
…
an
Стратегии
игрока
Р1
16.10.2018
a1
a 11
…
a 1j
…
a 1n
…
…
…
…
…
…
ai
a i1
…
a ij
…
a in
…
…
…
…
…
…
am
a m1
…
a mj
…
a mn
25
26. Решение матричных игр в чистых стратегиях
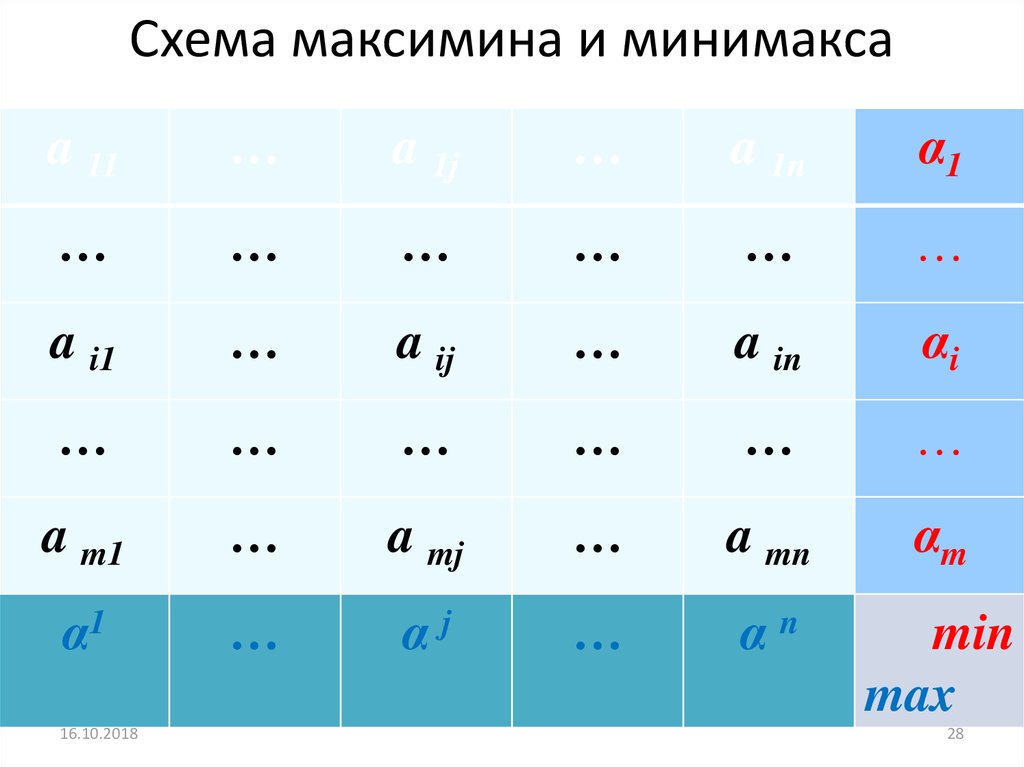
1. Если 1-й игрок выбрал стратегию i, то в худшемслучае он выиграет min(j) a ij при 1<j<n.
Поэтому он всегда может гарантировать себе
выигрыш ά = max(i) αi = max(i) min(j) a ij ,
обозначим его ά – нижняя цена игры, или
максимин, соответствующая стратегия 1-го
игрока называется максиминной. Таким
образом нижняя цена игры ά есть
максимальный гарантированный выигрыш
1-го игрока , какую бы стратегию не выбрал
2-ой игрок.
16.10.2018
26
27. Решение матричных игр в чистых стратегиях
1. Второй игрок, выбрав стратегию j, в худшемслучае проиграет max(i) a ij при 1<i<m, а значит,
может гарантировать себе проигрыш , α =
min(j) αj = min(j) max(i) a ij обозначим его α= β верхняя цена игры, или минимакс,
соответствующая стратегия 2-го игрока
называется минимаксной. Итак, верхняя цена
игры α = β есть минимально гарантированный
проигрыш 2-го игрока при любом выборе
стратегии 1-ым игроком.
16.10.2018
27
28. Схема максимина и минимакса
a 11…
a 1j
…
a 1n
α1
…
…
…
…
…
…
a i1
…
a ij
…
a in
αi
…
…
…
…
…
…
a m1
…
a mj
…
a mn
αm
α1
…
αj
…
αn
min
max
16.10.2018
28
29. Орлянка. Нижняя цена игры. максимин
1-1
-1
-1
1
-1
-1
α 1 = α 2 = -1, α = -1 - нижняя цена игры
16.10.2018
29
30. Орлянка. Верхняя цена. Минимакс.
1-1
-1
1
1
1
1
α1 = α2 = 1, ά = 1 - верхняя цена игры
α = -1 нижняя цена игры < 1 = ά
16.10.2018
30
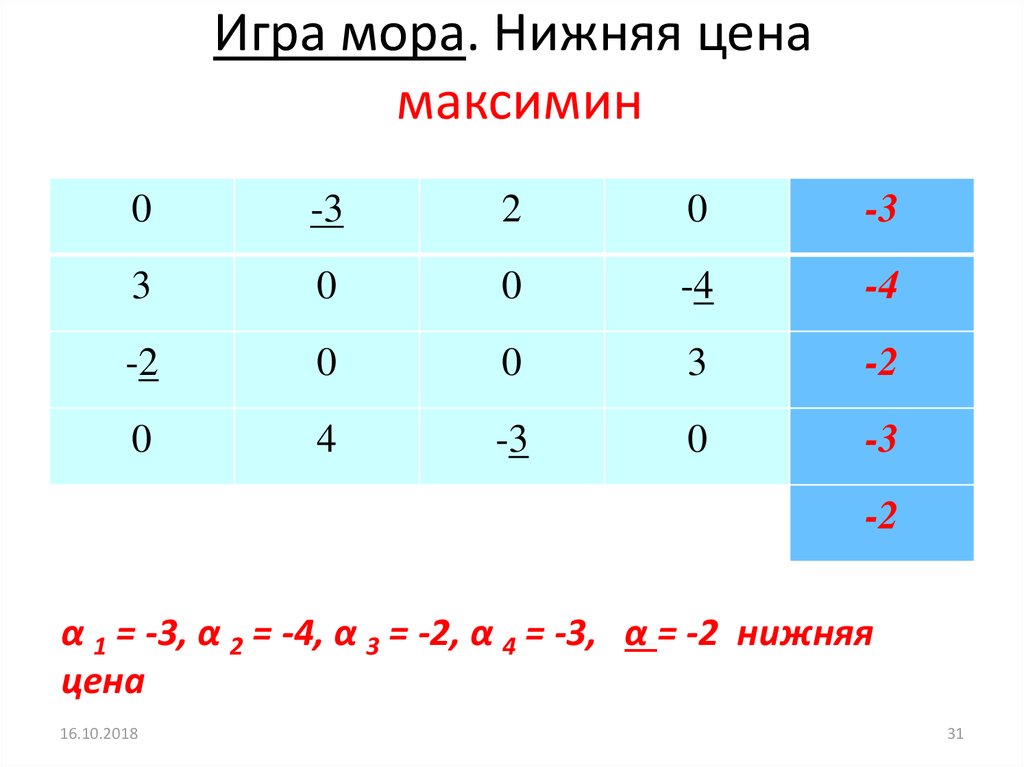
31. Игра мора. Нижняя цена максимин
0-3
2
0
-3
3
0
0
-4
-4
-2
0
0
3
-2
0
4
-3
0
-3
-2
α 1 = -3, α 2 = -4, α 3 = -2, α 4 = -3, α = -2 нижняя
цена
16.10.2018
31
32. Игра мора. Верхняя цена Минимакс.
0-3
2
0
3
0
0
-4
-2
0
0
3
0
4
-3
0
3
4
2
3
2
α 1 = 3, α 2 = 4, α 3 = 2, α 4 = 3, ά = 2.
α = -2 нижняя цена игры < 2 = ά
16.10.2018
32
33. Решение матричных игр в чистых стратегиях
1. Справедливо неравенство: α < ά .2. В игре Г естественно считать оптимальной такую
ситуацию (i,j), от которой ни одному из игроков
невыгодно отклоняться.
3. Ситуация (i*,j*) называется ситуацией равновесия, или
седловой точкой, если для любых 1<i<m, 1<j<n ,
выполняется неравенство a ij* < a i*j* < a i*j .
Соответствующие стратегии i*, j* называются
оптимальными чистыми стратегиями 1-го и 2-го
игроков, а число a i*j* называется ценой игры. Элемент
a i*j* является одновременно минимумом в своей
строке и максимумом в своем столбце.
4. Ситуация равновесия существует тогда и только тогда,
когда α = ά (это значение и является ценой игры ).
16.10.2018
33
34. Решение матричных игр в чистых стратегиях
1. Если α = ά , то говорят, что матричная игра имеетрешение в чистых стратегиях. Соответствующие
максиминная и минимаксная стратегии (a i0 и a j0 )
называются оптимальными (чистыми)
стратегиями матричной игры. Цена игры α = ά
равна максимальному гарантированному
выигрышу 1-го игрока и минимальному
гарантированному проигрышу 2-го игрока. При α
= ά имеет место наилучшее решение для обоих
игроков.
2. Если α < ά , то говорят, что матричная игра не
имеет решения (в чистых стратегиях).
3. Для одних игр выполняется равенство, а для других
неравенство (орлянка, мора).
16.10.2018
34
35. Решение матричных игр в чистых стратегиях
• Появление равенства α = ά или неравенстваα < ά целиком обусловлено только платежной
матрицей А.
• Для любой матрицы А с размерами m x n
справедливо следующее утверждение: если
max(i) min(j) a ij = min(j) max(i) a ij = ν , то
существует элемент a i0 j0 матрицы А такой, что
для любого номера i (1,2,3,….m) и j (1,2,3,…n)
имеет место цепочка неравенств:
a i j0 < a i0 j0 < a i0 j и ν = a i0 j0 . ( это седловой
элемент ( седловая точка) матрицы А.
Справедливо и обратное утверждение.
16.10.2018
35
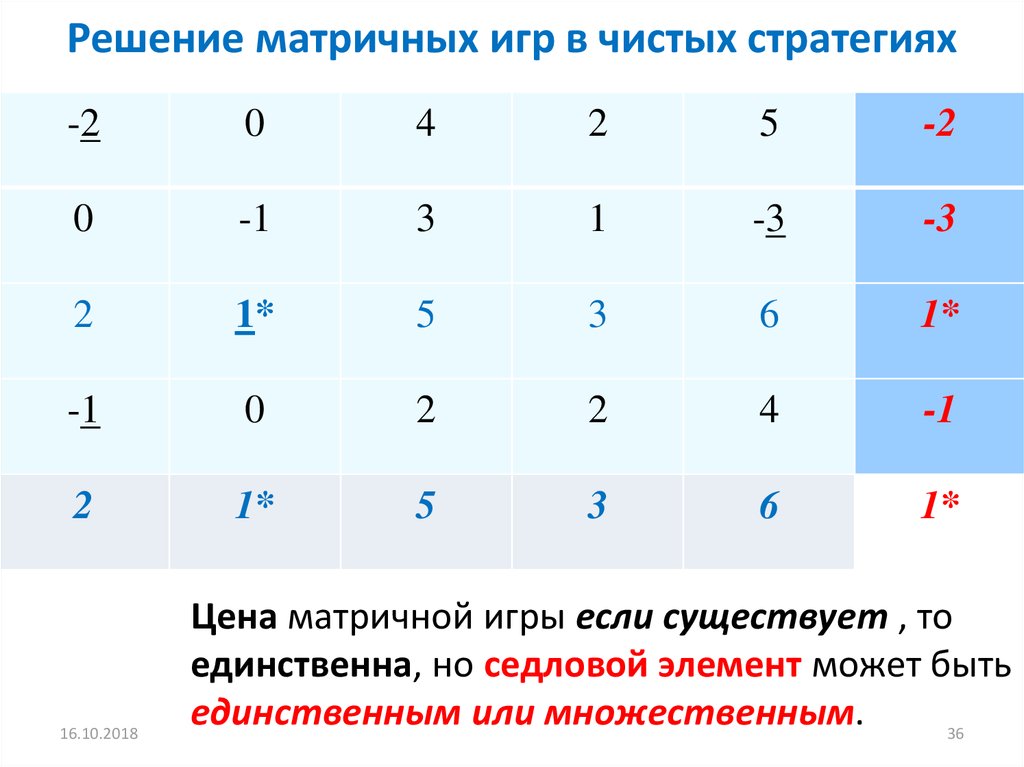
36. Решение матричных игр в чистых стратегиях
-20
4
2
5
-2
0
-1
3
1
-3
-3
2
1*
5
3
6
1*
-1
0
2
2
4
-1
2
1*
5
3
6
1*
16.10.2018
Цена матричной игры если существует , то
единственна, но седловой элемент может быть
единственным или множественным.
36
37. Решение матричных игр в чистых стратегиях
• Доминирование в теории игр — ситуация, прикоторой одна из стратегий некоторого игрока
дает больший выигрыш, нежели другая, при
любых действиях его оппонентов. Обратное
понятие, нетранзитивность, возникает, если
некоторая стратегия может давать меньшие
выигрыши, чем другая, в зависимости от
поведения остальных участников.
• Понятие доминирования используется при
решении или упрощении некоторых типов
некооперативных игр.
16.10.2018
37
38. Матричные игры
• Рассмотрим матричную игру( конечнаяигра двух лиц с нулевой суммой,
антагонистичная игра).
• Первый игрок располагает m стратегиями.
• Второй игрок n стратегиями.
• При выборе игроками Ai и Bj стратегий
возникает ситуация характеризующаяся
выигрышем первого игрока , равным aij.
• Числа aij являются элементами матрицы A
с размерностью m на n.
39. Матричные игры
a11a21
A
a
m1
a12
a22
am 2
A1 , A2 , , Am
B1 , B2 , , Bn
a
ij mxn
R
a1n
a2 n
a
ij
mxn
amn
40.
Платежная матрица матричной игрыB1
B2
Bn
A1
a11
a12
…
a1n
A2
a21
a22
…
a2n
…
…
…
…
…
Am
am1
am2
…
amn
41.
Bn…
a1n
1
a22
…
a2n
2
…
…
…
…
…
Am
am1
am2
…
amn
m
1
2
…
n
B1
B2
A1
a11
a12
A2
a21
…
Нижняя цена игры (максимин):
max min aij max i
i
j
i
Верхняя цена игры (минимакс):
min max aij min j
j
i
j
42.
Пример 1. Найти нижнюю и верхнюю чистыецены матричной игры:
4 4 5
A 3 5 7
5 6 6
max i max 4; 3; 5 5
i
min j min 5; 6; 7 5
j
a31 v 5
43.
Пример 2. Найти нижнюю и верхнюю чистыецены матричной игры:
7 1 9
A 6 8 4
1 2 0
4
7
4 v 7
44. Чистые и смешанные стратегии игроков
A3 : x 0; 0; 1B1 : y 1; 0; 0
Определение:
Чистая стратегия игрока – это возможный ход игрока,
выбранный им с вероятностью, равной единице.
x 0, ,0, 1, 0, ,0
Ai , B j : y 0, ,0, 1, 0, ,0
45.
46.
47.
• Но в некоторых играх естественно ввести врассмотрение также смешанные стратегии. Под
смешанной стратегией понимают
распределение вероятностей на чистых
стратегиях.
• В частном случае, когда множество чистых
стратегий каждого игрока конечно,
Xi =
{x1i , . . . , xni i } (соответствующая игра называется
конечной), смешанная стратегия представляется
вектором вероятностей соответствующих
чистых стратегий:
μi = (μ1i, . . . , μni i ).
16.10.2018
47
48.
• Обозначим множество смешанных стратегийi-го игрока через Mi:
M i i 0, k 1, , ni ; 1
k
i
1
i
ni
i
• Стандартное предположение теории игр
состоит в том, что если выигрыш—случайная
величина, то игроки предпочитают действия,
которые приносят им наибольший ожидаемый
выигрыш.
• Ожидаемый выигрыш i-го игрока,
соответствующий набору смешанных
стратегий всех игроков (μ1, . . . , μm),
вычисляется по формуле:
16.10.2018
48
49.
n1nm
k1 1
k m 1
U i , i u x , , x
ki
1
km
m i
ki
1
km
m
• Ожидание рассчитывается в предположении, что
игроки выбирают стратегии независимо (в
статистическом смысле). Поскольку игрок
максимизирует ожидаемый выигрыш, то он будет
смешивать несколько разных стратегий, только если
они дают ему одинаковый выигрыш (при данных
стратегиях других игроков). Смешанные стратегии
можно представить как результат рандомизации
игроком своих действий, т. е. как результат их
случайного выбора.
16.10.2018
49
50.
• Набор смешанных стратегийμ
= (μ1 , . . . , μm) является равновесием Нэша
в смешанных стратегиях, если стратегия
μ*i каждого игрока i = 1, . . . , n является
наилучшим для него откликом на стратегии
других игроков μ*−i:
U ,
16.10.2018
*
i
*
i
max U ,
i M i
i
*
i
50
51. Определение. Смешанной стратегией первого (второго) игрока называется вектор
x x1 , x2 ,..., xm , xi 0, i 1, m,y y1 , y2 ,..., yn ,
m
x
i 1
i
1
y j 0, i 1, n, y j 1
j 1
n
Определение. Если xi>0, yj>0, игра называется
активной
52.
Платежная функция игры:n
m
f x , y aij xi y j
j 1 i 1
Определение. Стратегии
x * x1* , x2* ,..., xm* ,
y * y1* , y2* ,..., yn*
называются оптимальными, если для произвольных
стратегий x x1 , x2 ,..., xm , y y1 , y2 ,..., yn
выполняется условие
f x, y f x , y f x , y
*
*
*
*
53.
Определение. Решением игры называетсясовокупность оптимальных стратегий и
цены игры
Цена игры:
f x ,y v
*
*
Теорема (об активных стратегиях). Если один
игрок придерживается своей оптимальной
смешанной стратегии, то выигрыш остается
неизменным и равным цене игры, если другой
игрок не выходит за пределы своих активных
стратегий.
54.
Теорема фон Неймана (основная теоремаматричных игр). Любая матричная игра имеет
по крайней мере одно решение в смешанных
стратегиях – две оптимальные стратегии и
соответствующую им цену:
x , y ,v f x , y
*
*
*
*
55.
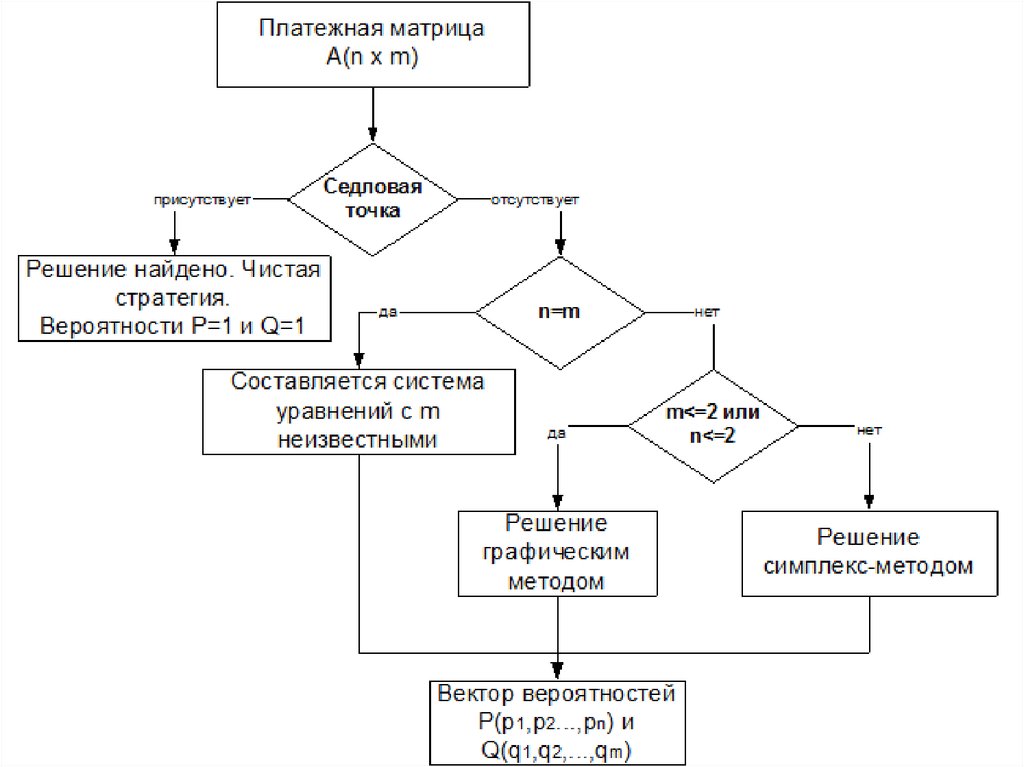
56. Методы решения матричных игр
1. Игра имеет седловой элемент в платежнойматрице.
В этом случае игрок 1 имеет чистую
максиминную стратегию, а игрок 2 чистую минимаксную стратегию, и при
этом α= = . Тогда говорят, что игра
решается в чистых стратегиях.
57. Методы решения матричных игр
2. Игра с платежной матрицей 2х2 безседлового элемента.
B1
B2
A1
a11
a12
х1
A2
a21
a22
х2
у1
у2
a x a x v
a x a x v
x
x
1
*
11 1
*
12 1
*
1
*
21 2
*
22 2
*
2
(если 2-й игрок играет только В1)
(если 2-й игрок играет только В2)
58.
a22 a21x
a11 a22 a12 a21
*
1
a11 a12
x 1 x
a11 a22 a12 a21
*
2
*
1
a22 a11 a12a21
v
a11 a22 a12 a21
59.
a y a12 y v (если 1-й игрок играет только A )a y a22 y v (если 1-й игрок играет только A )
y
y
1
*
11 1
*
21 1
*
1
*
2
*
2
*
2
a22 a12
y
a11 a22 a12 a21
*
1
a11 a21
y 1 y
a11 a22 a12 a21
*
2
*
1
1
2
60.
Пример. Найти смешанные стратегии игроков для игры сматрицей
1 3
1
A
2
y1*
A
2 1
*
*
3 x1*
x1 1 / 3, x2 2 / 3, v 5 / 3
*
1 x2
y1* 2 / 3, y2* 1 / 3
y1*
1x1* 2 x2* v
*
*
3
x
1
x
v
1
2
*
x*
x2 1
1
1/ 3; 2 / 3 ; 2 / 3; 1/ 3 ;
1y1* 3 y2* v
*
*
2
y
1
y
v
1
2
*
y*
y2 1
1
5/ 3
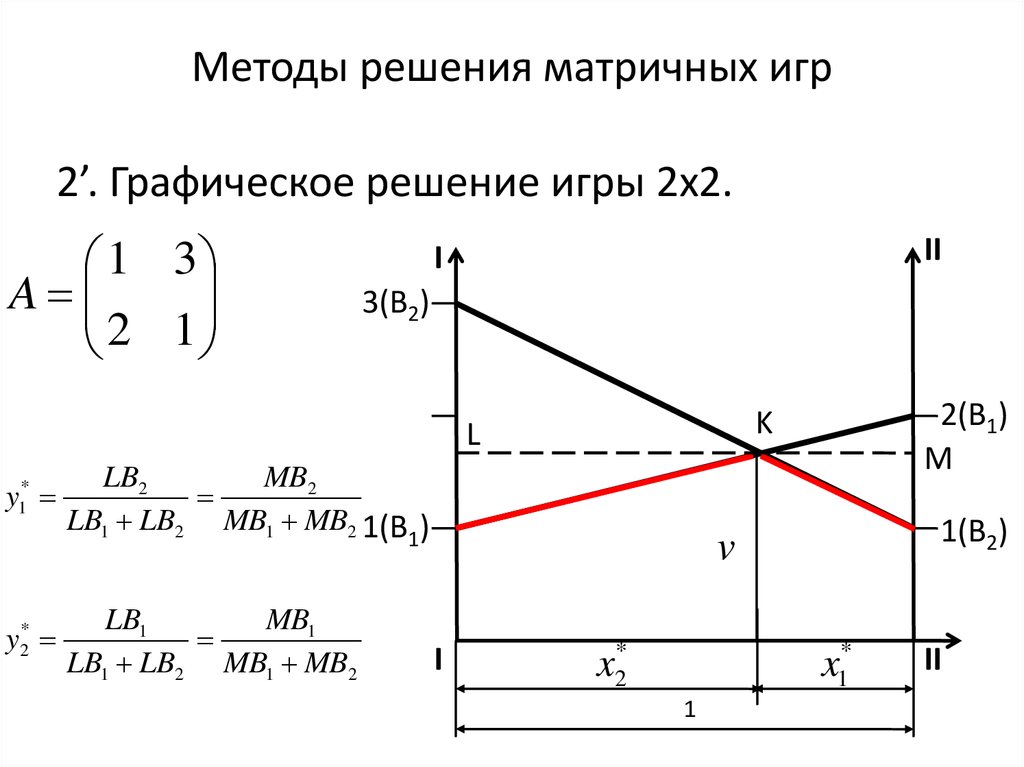
61. Методы решения матричных игр
2’. Графическое решение игры 2х2.1 3
A
2 1
II
I
3(B2)
L
y1*
y2*
LB2
MB2
LB1 LB2 MB1 MB2 1(B )
1
LB1
MB1
LB1 LB2 MB1 MB2
2(B1)
M
K
1(B2)
v
I
x2*
x1*
1
II
62. Методы решения матричных игр Решение игр вида 2хn и mх2
• У таких игр всегда имеется решение, содержащеене более двух активных стратегий для
каждого из игроков. Если найти эти активные
стратегии, то игра 2 х n или m х 2 сводится к
игре 2 х 2, которую мы уже умеем решать.
Поэтому игры 2 х n и m х 2 решают обычно
графоаналитическим методом.
• Следовательно активные стратегии
позволяют упростить задачу также, как и
доминирование.
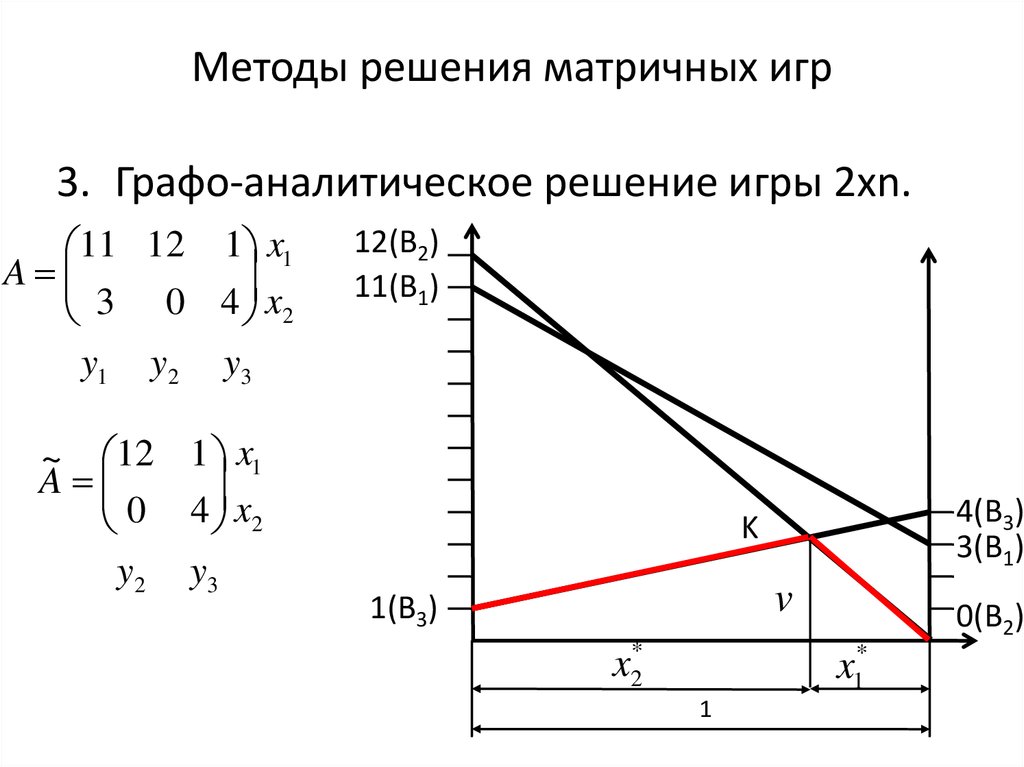
63. Методы решения матричных игр
3. Графо-аналитическое решение игры 2хn.11 12 1 x1
A
3 0 4 x2
y1 y2 y3
~ 12 1 x1
A
0 4 x2
y 2 y3
12(B2)
11(B1)
4(B3)
3(B1)
K
v
1(B3)
x2*
0(B2)
*
1
x
1
64.
~ 12 1 x1A
0 4 x2
y 2 y3
12 x1* 0 x2* v
*
*
1
x
4
x
v
1
2
*
x*
x
1
2
1
x1* 4 / 15, x2* 11 / 15, v 3,2
12 y1* 1 y2* v
*
*
0
y
4
y
v
1
2
*
y*
y2 1
1
4 / 15; 11/ 15 ; 0; 1/ 5; 4 / 5 ;
y1* 1 / 5,
y2* 4 / 5
3,2
65. Методы решения матричных игр
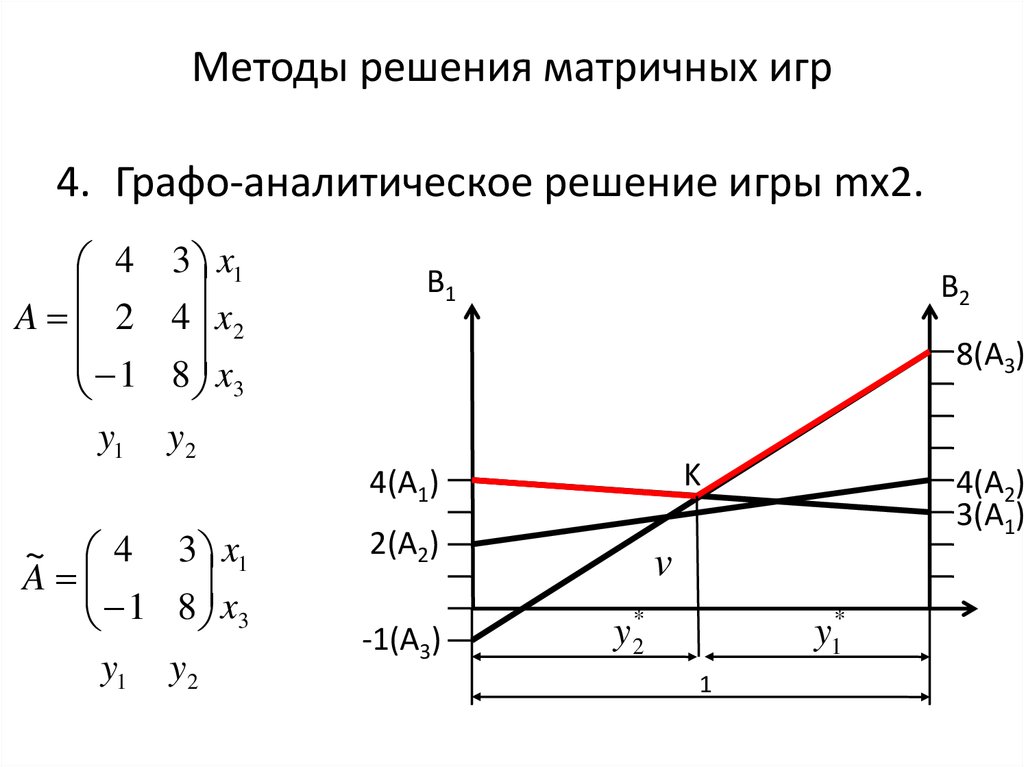
4. Графо-аналитическое решение игры mx2.4
A 2
1
y1
3 x1
4 x2
8 x3
B1
B2
8(A3)
y2
K
4(A1)
~ 4 3 x1
A
1 8 x3
y1 y2
2(A2)
-1(A3)
4(A2)
3(A1)
v
y
*
2
*
1
y
1
66.
*4
3
x
~
1*
A
1 8 x3
y1* y 2*
4 x1* 1x3* v
*
*
3
x
8
x
v
1
3
x* x* 1
3
1
4 y1* 3 y2* v
*
*
y
8
y
v
1
2
*
y*
y2 1
1
x 0,9, x 0,1, v 3,5
*
1
y1* 0,5,
*
3
y2* 0,5
0,9; 0; 0,1 ; 0,5; 0,5 ;
3,5
67. Методы решения матричных игр
5. Игры с доминирующими и дублирующимистратегиями.
ai1 ak1 , ai 2 ak 2 ,..., ain akn .
a1 j , , a1l ,
a2 j , , a2l ,
...
amj , , aml .
y 0
*
l
x 0
*
k
68. Первый метод, используемый для уменьшения размерности матрицы, основан на одном из важнейших понятий в теории игр - понятии
доминированиястратегий.
• Если i-я строка поэлементно не меньше (≥) j-й
строки, то говорят, что i-я строка доминирует
над j-й строкой.
• Поэтому игрок A не использует j-ю стратегию,
так как его выигрыш при i-й стратегии не
меньше, чем при j-й стратегии, вне зависимости
от того, как играет игрок B.
69. Первый метод, используемый для уменьшения размерности матрицы, основан на одном из важнейших понятий в теории игр - понятии
доминированиястратегий.
• Если i-й столбец поэлементно не меньше (≥) j-го
столбца, то говорят, что j-й столбец доминирует
над i-м столбцом. Поэтому игрок B не
использует i-ю стратегию, так как его проигрыш
(равный выигрышу игрока A) при j-й стратегии
не больше (≤), чем при i-й стратегии, вне
зависимости от того, как играет игрок A.
70. Первый метод, используемый для уменьшения размерности матрицы, основан на одном из важнейших понятий в теории игр - понятии
доминированиястратегий.
• Стратегии, над которыми доминируют другие
стратегии, надо отбросить и приписать им нулевые
вероятности. На цене игры это никак не скажется.
Зато размер матрицы игры понизится. С этого и
нужно начинать решение игры.
• Частный случай доминирования является
дублирование стратегий.
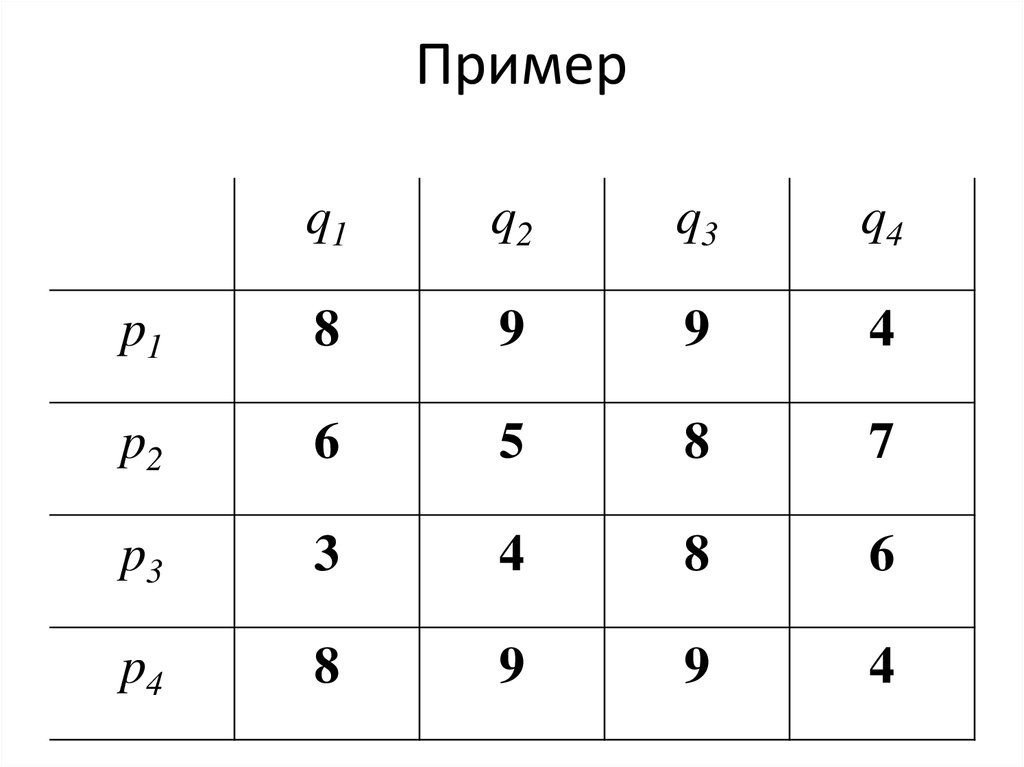
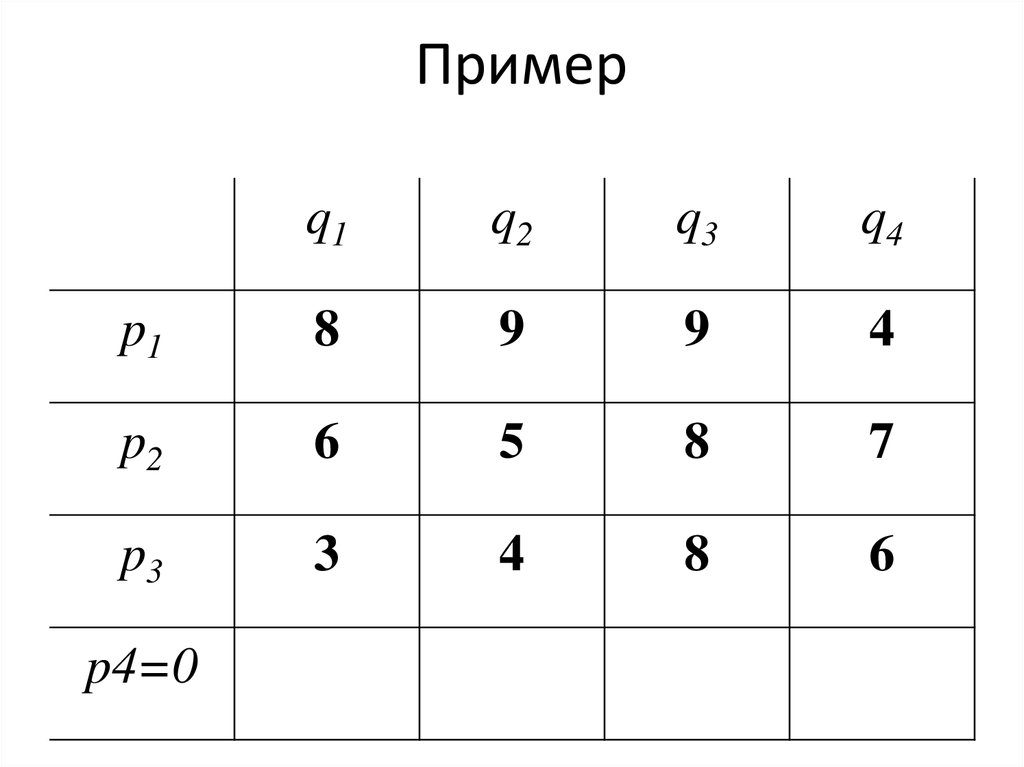
71. Пример
q1q2
q3
q4
p1
8
9
9
4
p2
6
5
8
7
p3
3
4
8
6
p4
8
9
9
4
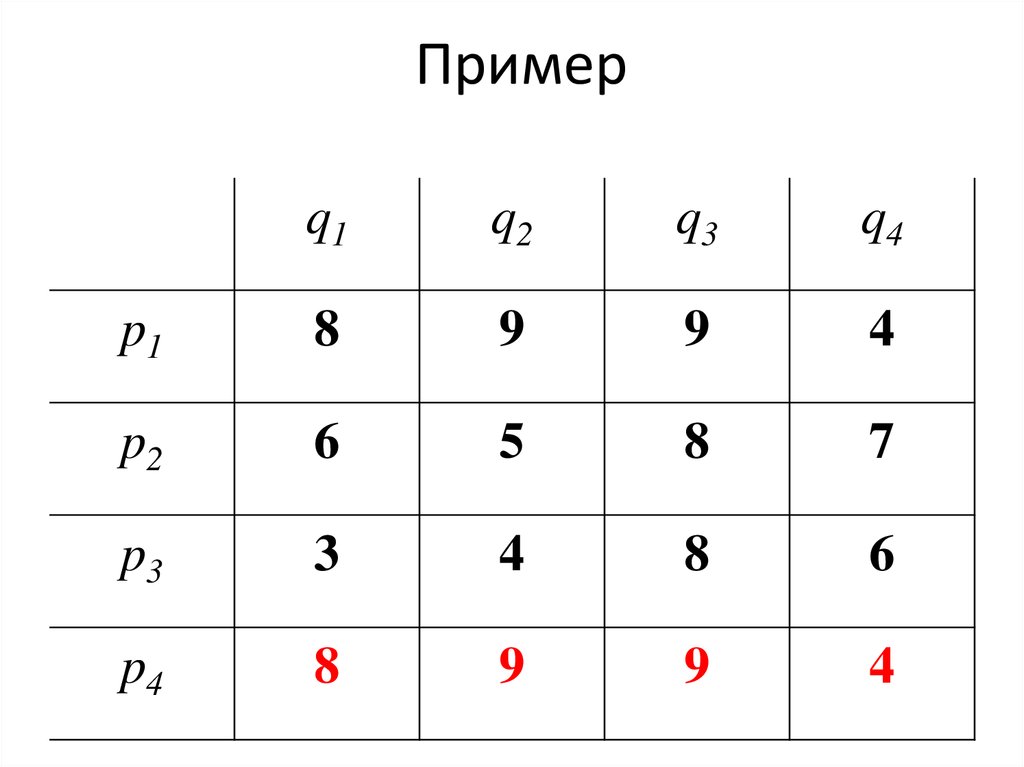
72. Пример
q1q2
q3
q4
p1
8
9
9
4
p2
6
5
8
7
p3
3
4
8
6
p4
8
9
9
4
73. Пример
q1q2
q3
q4
p1
8
9
9
4
p2
6
5
8
7
p3
3
4
8
6
p4=0
74. Пример
q1q2
q3
q4
p1
8
9
9
4
p2
6
5
8
7
p3
3
4
8
6
p4=0
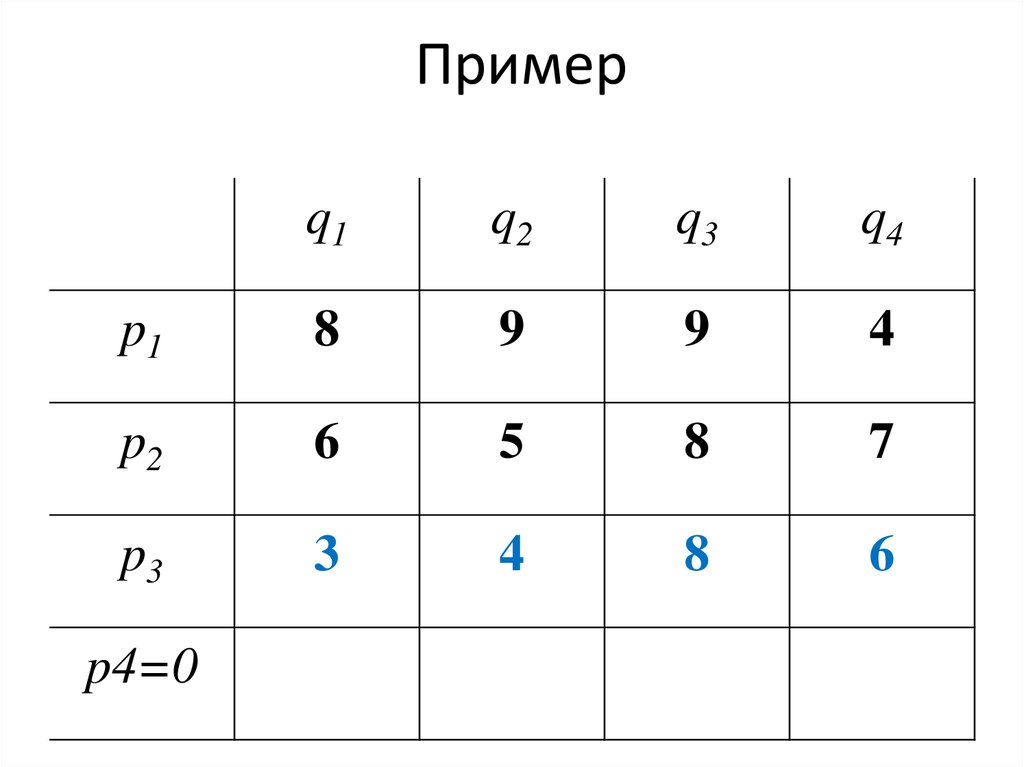
75. Пример
q1q2
q3
q4
p1
8
9
9
4
p2
6
5
8
7
p3=0
p4=0
76. Пример
q1q2
q3
q4
p1
8
9
9
4
p2
6
5
8
7
p3=0
p4=0
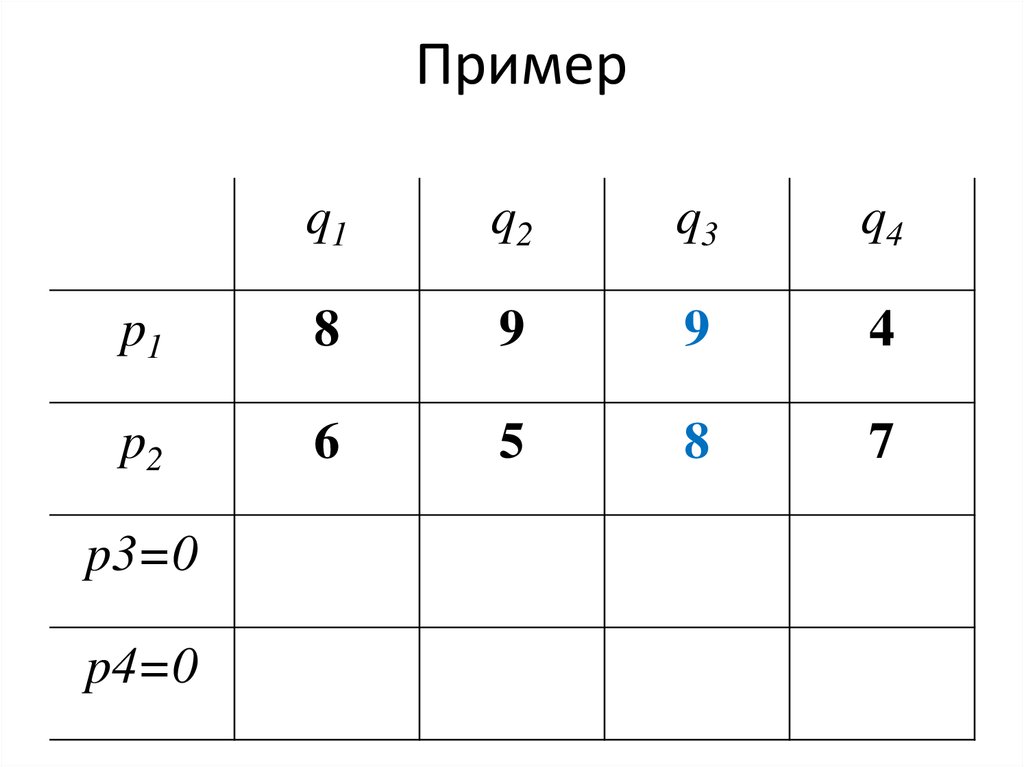
77. Пример
p1p2
p3=0
p4=0
q1
8
6
q2
9
5
q3=0
q4
4
7
Дальнейшее упрощение невозможно.
Мы свели игру 4×4 к игре 2×3.
78. Пример 2 - упростить игру
q1q2
q3
q4
p1
4
5
6
7
p2
3
4
6
5
p3
7
6
10
8
p4
8
5
4
3
79. Дублирование и доминирование
• Замечание. Если игра m×n имеетседловую точку, то после упрощений
платёжной матрицы мы всегда
получим игру 1×1.
80. Методы решения матричных игр
6. Эквивалентное преобразованиеплатежной матрицы.
Теорема. Оптимальные смешанные стратегии х* и у*
соответственно 1-го и 2-го игроков в матричной игре
с ценой v будут оптимальными и в матричной игре
с ценой v’=bv+c, где
b 0, c R
Пример:
1,2 1,8
A
0,6 0,9
~ 6 12
b 10, c 6 A
0 3
a
ba
ij mxn
ij
c mxn
81. Пример 3
• Задана платежная матрица:400 -300 600
-200 -400 500
800 700 -100
• Необходимо упростить матрицу.
8 1 10
b=0.01
2 0 9
c=4
12 11 3
82. Методы решения матричных игр
7. Решение матричной игры mxn (общий случай).Здесь матричная игра сводится к задаче
линейного программирования. Пусть дана игра
с матрицей:
y1
y2
yn
x1
a11
a12
…
a1n
x2
a21
a22
…
a2n
…
…
…
…
…
xm
am1
am2
…
amn
Все элементы матрицы при этом считаются неотрицательными;
Тогда цена игры будет положительной, v>0. Вводятся
новые переменные:
yj
xi
ti , u j , i 1,..., m; j 1,..., n
v 0
aij 0
v
v
83.
Теперь матричная игра сводится к следующей задачелинейного программирования относительно
1-го игрока:
a11t1 a21t 2 ... am1t m 1,
a t a t ... a t 1,
22 2
m2 m
12 1
...
a t a t ... a t 1,
1n 1
2n 2
mn m
1
T t1 t 2 ... t m min,
v
ti 0, i 1,..., m.
84.
или к двойственной ей – для 2-го игрока:a11u1 a12u 2 ... a1n u n 1,
a u a u ... a u 1,
22 2
2n n
21 1
...
a u a u ... a u 1,
m1 1
m2 2
mn n
1
Z u1 u 2 ... u n max
v
u j 0, j 1,..., n.
85. Понятие об игре с природой
П1П2
Пn
A1
a11
a12
…
a1n
A2
a21
a22
…
a2n
…
…
…
…
…
Am
am1
am2
…
amn
p
p1
p2
…
pn
Матрица рисков:
r11
r21
R
r
m1
r1n
r22 r2 n
, rij max aij aij
i
rm 2 rmn
r12
86. Понятие об игре с природой
• Любую хозяйственную деятельность человекаможно рассматривать как игру с природой. В
широком смысле под "природой" понимается
совокупность неопределенных факторов;
влияющих на эффективность принимаемых
решений. Безразличие природы к игре (выигрышу)
к возможности получения экономистом
(статистиком) дополнительной информации о ее
состоянии отличают игру экономиста с природой от
обычной матричной игры, в которой принимают
участие два сознательных игрока.
• Данный тип задач относится к задачам принятия
решений в условиях неопределенности.
87. Понятие об игре с природой
• Предположим, что ЛПР рассматриваетнесколько возможных решений: i = 1,…,m.
Ситуация, в которой действует ЛПР, является
неопределенной. Известно лишь, что
наличествует какой-то из вариантов: j = 1,…, n.
Если будет принято i-e решение, а ситуация
есть j-я , то фирма, возглавляемая ЛПР,
получит доход aij. Матрица A = (aij) называется
матрицей последствий (возможных решений).
88. Понятие об игре с природой
• В этой ситуации полной неопределенности могутбыть высказаны лишь некоторые рекомендации
предварительного характера. Они не обязательно
будут приняты ЛПР. Многое будет зависеть,
например, от его склонности к риску.
• Оценим риск, который несет i-e решение. Нам
неизвестна реальная ситуация. Но если бы ее знали,
то выбрали бы наилучшее решение, т.е.
приносящее наибольший доход. Т.е. если ситуация
есть j-я , то было бы принято решение, дающее
доход aij.
89. Понятие об игре с природой
• Значит, принимая i-e решение мы рискуемполучить не aj, а только aij, значит принятие
i-го решения несет риск недобрать rij = aj aij. Матрица R = (rij) называется матрицей
рисков.
• Уникальные единичные случайные
явления связаны с неопределенностью,
массовые случайные явления обязательно
допускают некоторые закономерности
вероятностного характера.
90. Пример:
25
8
4
Пусть матрица последствий есть:
Q= 2 3 4 12
8 5 3 10
1 4 2 8
Составим матрицу рисков.
Имеем q1 = max(qi1) = 8, q2 = 5, q3 = 8, q4 = 12.
Следовательно, матрица рисков есть 6 0 0 8
rij = qj - qij.
6 2 4 0
R = (rij)
R= 0 0 5 2
716 4
91. Понятие об игре с природой
• Ситуация полной неопределенностихарактеризуется отсутствием какой бы то
ни было дополнительной информации.
• Какие же существуют правиларекомендации по принятию решений в
этой ситуации?
92. Понятие об игре с природой
1. Правило Вальда (правило крайнегопессимизма). Рассматривая i-e решение
будем полагать, что на самом деле ситуация
складывается самая плохая, т.е. приносящая
самый малый доход ai Но теперь уж
выберем решение i0 с наибольшим ai0. Итак,
правило Вальда рекомендует принять
решение i0, такое что:
ai0 = max ai = max ( min aij )
i
i
j
93.
• По критерию Вальда за оптимальнуюпринимается чистая стратегия, которая в
наихудших условиях гарантирует максимальный
выигрыш, т.е. a = max(min aij)
Критерий Вальда ориентирует статистику на
самые неблагоприятные состояния природы,
т.е. этот критерий выражает пессимистическую
оценку ситуации.
• Так, в вышеуказанном примере, имеем a1 = 2,
a2 = 2, a3 = 3, a4 = 1. Из этих чисел
максимальным является число 3. Значит,
правило Вальда рекомендует принять 3-е
решение.
94.
2. Правило Сэвиджа (правило минимальногориска). При применении этого правила
анализируется матрица рисков R = (rij).
Рассматривая i-e решение будем полагать, что
на самом деле складывается ситуация
максимального риска
bi = max [rij] ,
Но теперь уж выберем решение i0 с наименьшим
bi0. Итак, правило Сэвиджа рекомендует
принять решение i0, такое что
bi0 =min bi = min ( max rij )
i
i
j
95.
Критерий минимального риска Севиджа
рекомендует выбирать в качестве оптимальной
стратегии ту, при которой величина максимального
риска минимизируется в наихудших условиях, т.е.
обеспечивается:
a = min(max rij)
Kритерий Сэвиджа ориентирует статистику на
самые неблагоприятные состояния природы, т.е.
этот критерий выражает пессимистическую оценку
ситуации.
В рассматриваемом примере имеем b1 = 8, b2 = 6, b3
= 5, b4 = 7. Минимальным из этих чисел является
число 5. Т.е. правило Сэвиджа рекомендует
принять 3-е решение.
96.
3. Правило Гурвица (взвешивающеепессимистический и оптимистический подходы
к ситуации). Принимается решение i, на
котором достигается максимум:
λ min qij + (1-λ) max qij
где 0 < λ < 1
j
j
Значение λ выбирается из субъективных
соображений. Если λ приближается к 1, то
правило Гурвица приближается к правилу
Вальда, при приближении λ к 0, правило
Гурвица приближается к правилу "розового
оптимизма" (догадайтесь сами, что это
значит). (максимакс)
97.
Критерий Гурвица является критериемпессимизма - оптимизма.
Критерий Гурвица учитывает возможность как
наихудшего, так и наилучшего для человека
поведения природы.
• Как выбирается λ? Чем хуже последствия
ошибочных решений, тем больше желание
застраховаться от ошибок, тем λ ближе к 1.
• В вышеуказанном примере при λ= 1/2 правило
Гурвица рекомендует 2-е решение.
98.
4. Предположим, что в рассматриваемой схемеизвестны вероятности pj того, что реальная
ситуация развивается по варианту j. Именно
такое положение называется частичной
неопределенностью. Как здесь принимать
решение? Можно выбрать одно из следующих
правил.
• Правило максимизации среднего ожидаемого
дохода. Доход, получаемый фирмой при
реализации i-го решения, является случайной
величиной Qi с рядом распределения. Правило
рекомендует принять решение, приносящее
максимальный средний ожидаемый доход.
99.
4а. По критерию Байеса за оптимальныепринимается та стратегия (чистая) Ai, при
которой максимизируется средний выигрыш a
или минимизируется средний риск
r - max ∑(aijpj)
4б. Критерий Лапласа.
Если вероятности состояний природы
правдоподобны, для их оценки используют
принцип недостаточного основания Лапласа,
согласно которого все состояния природы
полагаются равновероятными, т.е.:
q1 = q2 = ... = qn = 1/n.
100. Пример
• Предположим, что в схеме из предыдущегопримера вероятности есть (1/2, 1/6, 1/6, 1/6).
• Математическое ожидание M[Qi] и есть средний
ожидаемый доход, обозначаемый Qi . Правило
рекомендует принять решение, приносящее
максимальный средний ожидаемый доход.
Q1 23 ; Q2 25 ; Q3 7; Q4 17
• Тогда
6
6
6
• Максимальный средний ожидаемый доход равен
7, соответствует третьему решению.
101. Пример
• Вычислим средние ожидаемые риски приуказанных выше вероятностях. Получаем:
R1 26 ; R2 4; R3 7 ; R4 32
6
6
6
• Минимальный средний ожидаемый риск равен
7/6, соответствует третьему решению.
• По правилу Лапласа просчитать
самостоятельно!
• В случае, если количество Парето-оптимальных
решений больше одного, то для определения
лучшего решения применяется взвешивающая
формула
102.
nКритерий Байеса:
1
p1 p2 ... pn
n
Критерий Вальда:
max ai max aij p j
i
i
j 1
1 n
max ai aij
i
n j 1
max min aij
j
i
m
a
max min
j
x
Критерий Сэвиджа:
x
ij i
i 1
S min max rij
i
j
m
S min max rij xi
x
j
i 1
103.
Критерий Гурвица:0,1
1
0
H max min aij 1 max aij
i
j
j
- «коэффициент пессимизма»
- критерий Вальда
- ситуация «крайнего оптимизма»
























































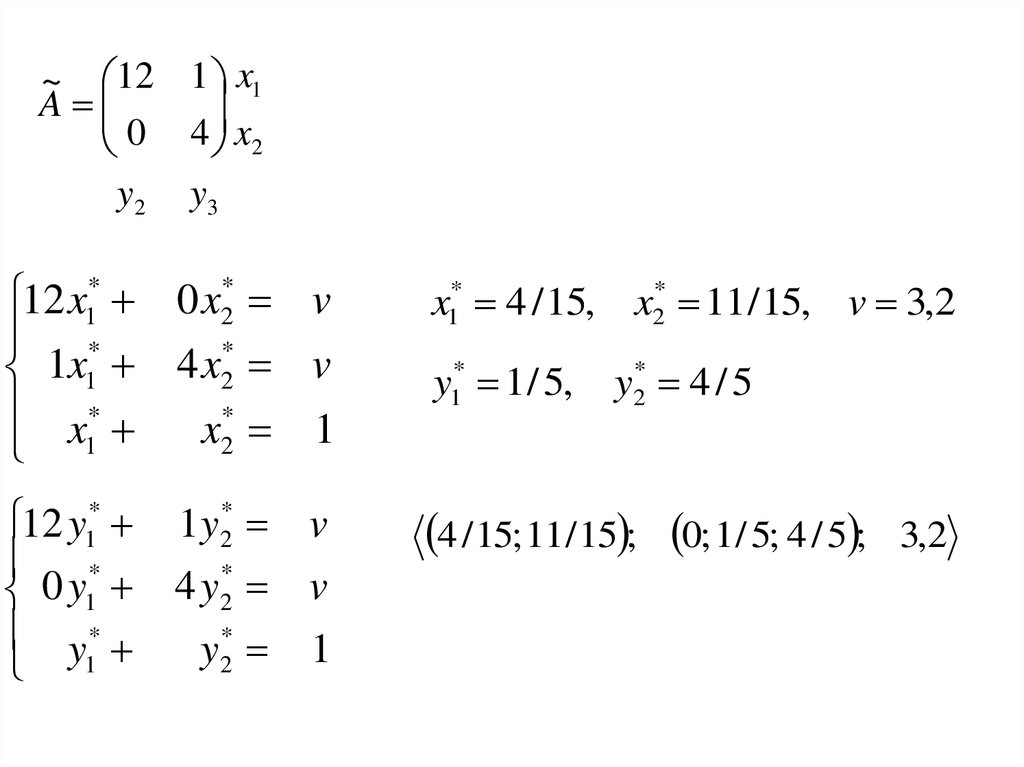
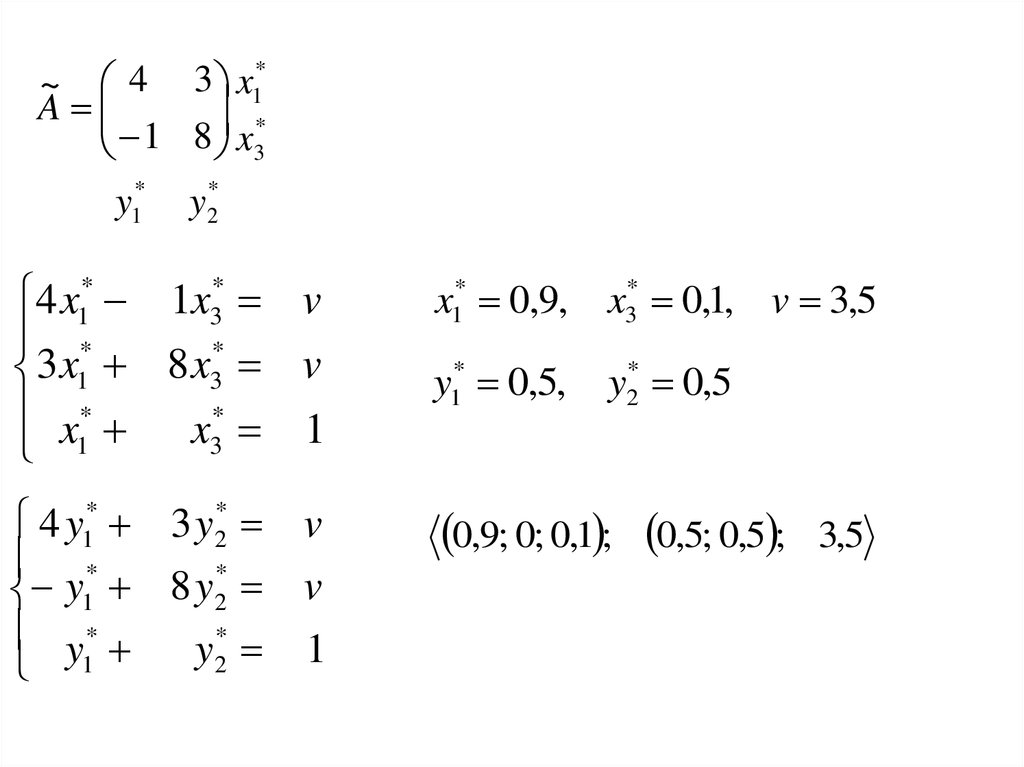
































 Математика
Математика








