Похожие презентации:
Введение в Matlab (Matrix Laboratory)
1.
12.
Спектр проблем:Матричный анализ;
Обработка сигналов и изображений;
Проектирование и анализ
радиочастотных цепей;
Задачи математической физики;
Оптимизационные задачи;
Обработку и визуализацию данных и
многое другое.
2
3.
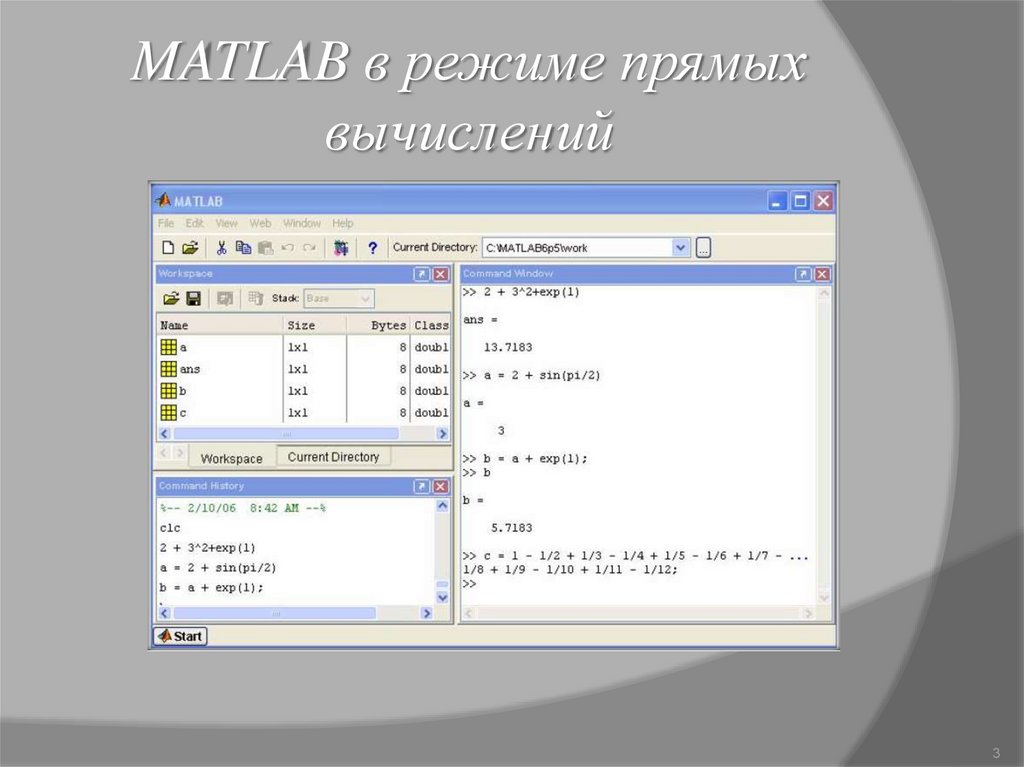
MATLAB в режиме прямыхвычислений
3
4.
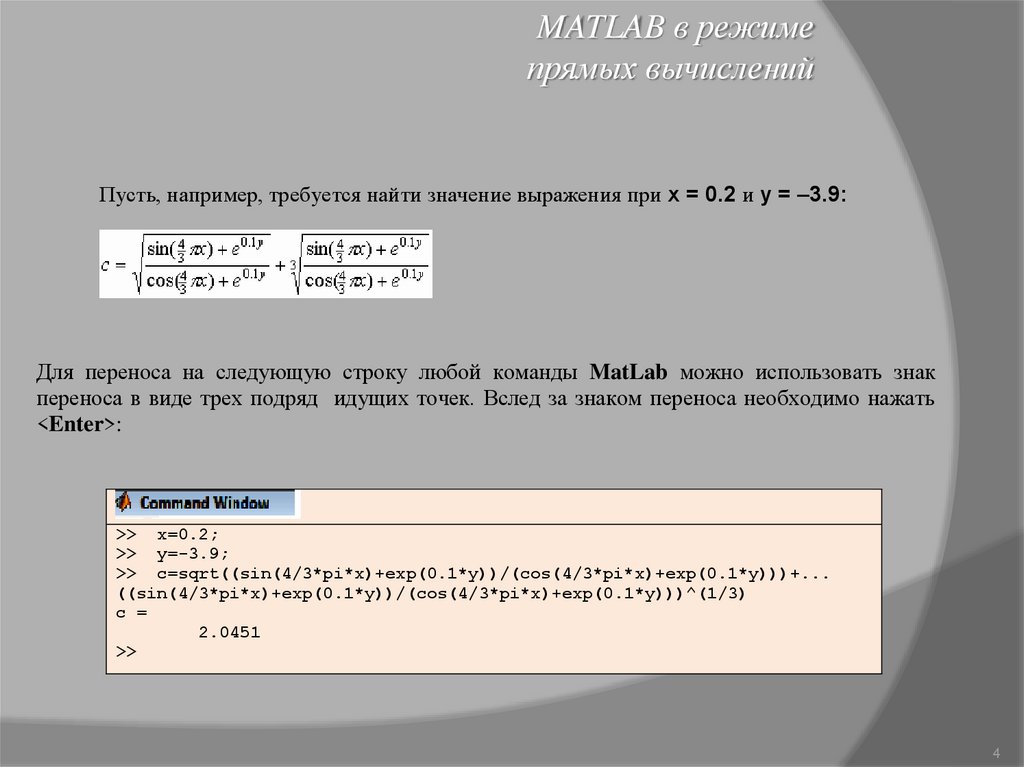
MATLAB в режимепрямых вычислений
Пусть, например, требуется найти значение выражения при x = 0.2 и y = –3.9:
Для переноса на следующую строку любой команды MatLab можно использовать знак
переноса в виде трех подряд идущих точек. Вслед за знаком переноса необходимо нажать
<Enter>:
>> x=0.2;
>> y=-3.9;
>> c=sqrt((sin(4/3*pi*x)+exp(0.1*y))/(cos(4/3*pi*x)+exp(0.1*y)))+...
((sin(4/3*pi*x)+exp(0.1*y))/(cos(4/3*pi*x)+exp(0.1*y)))^(1/3)
c =
2.0451
>>
4
5.
Основные объекты MATLABВсе числовые значения, с которыми оперирует
MatLab, в оперативной памяти компьютера представлены
вещественными или комплексными значениями double. Это
означает, что каждое вещественное число занимает 8 байт в
памяти и принимает по модулю значения из диапазона [10-308,
10+308], причем количество значащих десятичных цифр
достигает 16. Именно с такой точностью MatLab выполняет
все вычисления.
Ниже приводятся примеры представления чисел:
0
2
-3
2.301
0.00001
123.456е-24
-234.456е10
5
6.
Числа могут быть комплексными: z = Re(z) + Im(z)*i.Функция real(z) возвращает действительную часть
комплексного числа, Re(z), а функция imag(z) – мнимую,
Im(z). Для получения модуля комплексного числа
используется функция abs(z), а для вычисления фазы —
angle(Z). Ниже даны простейшие примеры работы с
комплексными числами:
>> abs(z)
ans =
>> i
3.6056
ans =
>> real(z)
ans =
0 + 1.0000i
2
>> j
>> imag(z)
ans =
ans =
0 + 1.0000i
3
>> z=2+3i
>> angle(z)
z=
ans =
2.0000 + 3.0000i
0.9828
6
7.
Форматы чиселКоманда format служит для установки формата из командной строки. Например,
обращение
>>
>>
Формат
short
long
short e
long e
short g
long g
hex
+
rational
format short e
Описание
Короткое число с плавающей точкой. Представляется с помощью
четырех цифр после десятичной точки ( по умолчанию)
Длинное число с плавающей точкой. Представляется с помощью
четырнадцати цифр после десятичной точки
Короткое число с плавающей точкой. Представляется с помощью пяти
разрядов, четыре из которых отводится под вывод дробной части
Длинное число с плавающей точкой. Представляется с помощью
шестнадцати разрядов, пятнадцать из которых отводится под вывод
дробной части
Выбирается наилучшая форма представления числа из форматов short
и short e
Выбирается наилучшая форма представления числа из форматов long и
long e
Число выводится в шестнадцатеричной форме
Символьное обозначение числа: «+» - положительное число; «-» отрицательное число; пробел - нулевое значение
Число выводится в дробном виде
Для иллюстрации различных
форматов рассмотрим число
х=4/3. В различных форматах
оно будет иметь следующий
вид:
format short 1.3333
format short e 1.3333E+000
format long
1.333333333333338
format long e
1.333333333333338E+000
7
8.
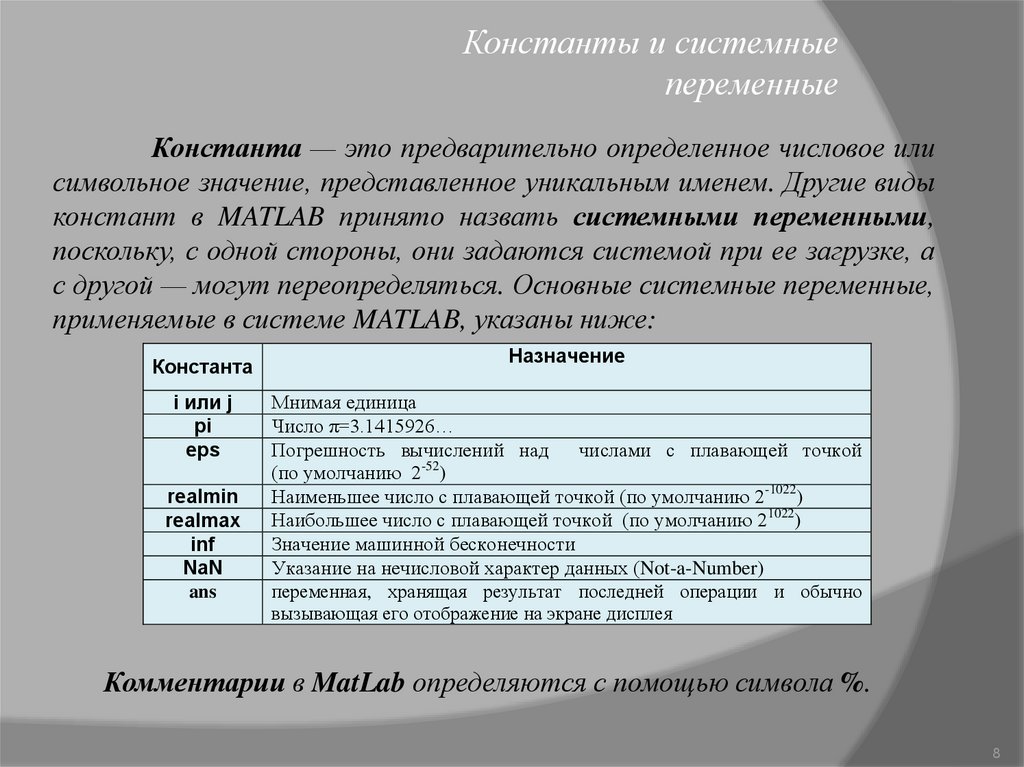
Константы и системныепеременные
Константа — это предварительно определенное числовое или
символьное значение, представленное уникальным именем. Другие виды
констант в MATLAB принято назвать системными переменными,
поскольку, с одной стороны, они задаются системой при ее загрузке, а
с другой — могут переопределяться. Основные системные переменные,
применяемые в системе MATLAB, указаны ниже:
Константа
i или j
pi
eps
realmin
realmax
inf
NaN
ans
Назначение
Мнимая единица
Число π=3.1415926…
Погрешность вычислений над
числами с плавающей точкой
-52
(по умолчанию 2 )
Наименьшее число с плавающей точкой (по умолчанию 2-1022)
Наибольшее число с плавающей точкой (по умолчанию 21022)
Значение машинной бесконечности
Указание на нечисловой характер данных (Not-a-Number)
переменная, хранящая результат последней операции и обычно
вызывающая его отображение на экране дисплея
Комментарии в MatLab определяются с помощью символа %.
8
9.
ПеременныеПеременные – это имеющие имена объекты, способные хранить
некоторые, разные по значению, данные. В зависимости от этих данных,
переменные могут быть числовыми или символьными, векторными или
матричными. При использовании переменных необходимо придерживаться правил:
имя переменной (ее идентификатор) может состоять из символов латинского
алфавита, знака подчёркивания и цифр, но начинаться обязательно с символа
алфавита;
прописные и строчные буквы различаются;
пробел не входит в имя переменной.
Для задания переменным определенных значений используется операция
присваивания, обозначаемая знаком равенства =.
>> a=3.25*(0.7-3.3/5.1)+2.3^3
a =
12.3391
>> b=5*(2.2+3.9i)+0.8
b =
11.8000 +19.5000i
>>
Для очистки рабочей области используется функция clear в разных формах,
например:
clear – уничтожение определений всех переменных;
clear х – уничтожение определения переменной х;
clear а, b, с – уничтожение определений нескольких переменных.
9
10.
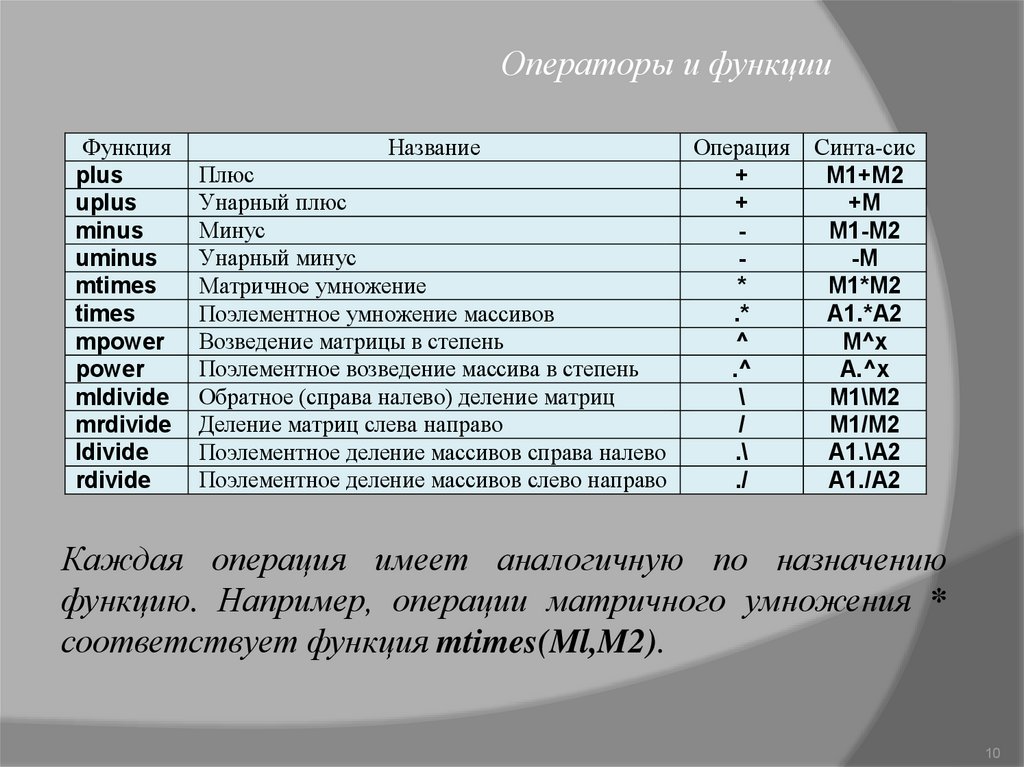
Операторы и функцииФункция
plus
uplus
minus
uminus
mtimes
times
mpower
power
mldivide
mrdivide
ldivide
rdivide
Название
Плюс
Унарный плюс
Минус
Унарный минус
Матричное умножение
Поэлементное умножение массивов
Возведение матрицы в степень
Поэлементное возведение массива в степень
Обратное (справа налево) деление матриц
Деление матриц слева направо
Поэлементное деление массивов справа налево
Поэлементное деление массивов слево направо
Операция
+
+
*
.*
^
.^
\
/
.\
./
Синта-сис
M1+M2
+M
М1-M2
-М
M1*M2
A1.*A2
М^х
A.^x
M1\M2
M1/M2
A1.\A2
A1./A2
Каждая операция имеет аналогичную по назначению
функцию. Например, операции матричного умножения *
соответствует функция mtimes(Ml,M2).
10
11.
Операторы и функцииТригонометрические функции (результат вычисляется в радианах)
sin, cos, tan, cot
Синус, косинус, тангенс и котангенс
sec, csc
Секанс, косеканс
Обратные тригономе-кие функции (результат вычисляется в рад.)
asin, acos,atan,atan2, acot
Арксинус, арккосинус, арктангенс и арккотангенс
asec, acsc
Арксеканс, арккосеканс
Гиперболические функции
sinh, cosh, tanh, coth
Гипербол. синус, косинус, тангенс и котангенс
sech, csch
Гиперболические секанс и косеканс
asinh, acosh, atanh, acoth
Гиперболические арксинус,
арккосинус, арктангенс и арккотангенс;
Экспоненциальная функция, логарифмы, степенные функции
exp
Экспоненциальная функция
log, log2, log10
Логарифм натуральный, по основанию 2 и 10
sqrt
Квадратный корень
Модуль, знак и функции для работы с комплексными числами
abs, sign
Модуль и знак числа
conj, imag, real
Комплексно-сопряжённое
mod, rem
Остаток от деления с учетом знака делимого и без
gcd, lcm
Наибольший и наименьший общий делитель
cell, fix, floor, round
округления
Со списком элементарных
функций
можно
ознакомиться, выполнив
команду help elfun, а со
списком
специальных
функций – с помощью
команды help specfun.
Функции могут быть
встроенными
(внутренними)
и
внешними,
или
тфункциями.
11
12.
Функции пользователя>> sc2 = inline('sin(x).^2+соs(у).^2')
sc2 =
Inline function:
sc2(x,y) = sin(x).^2+cos(у).^2
Можно также задавать свои функции в виде m-файлов. Например, можно в окне редактора mфайлов (открывается командой New в меню File) создать m- файл с именем sc2 и листингом:
function y=sc2(x,y)
y=sin(x).^2+cos(y).^2;
Записав его на диск, можно командой type sc2 вывести листинг созданной функции:
>> type sc2
function y=sc2(x,y)
y=sin(x).^2+cos(y).^2;
Обращение к функции, созданной описанными методами, задается как sc2(x,y), где на место х и
y подставляются значения переменных – аргументов функции пользователя. Например:
>> sс2(1,2)
ans =
0.8313
>> sc2(2,1)
ans =
1.1187
12
13.
Массивы. Способы формирование иоперации над ними.
Одним
из самых заметных и важных преимуществ
системы MATLAB над другими программными пакетами,
ориентированными на вычисления и программирование
это то, что она специально предназначенная для
проведения
сложных
вычислений
с
векторами,
матрицами и массивами – в том числе многомерными.
Двумерные
массивы в математике принято называть
матрицами. Любая строка и любой столбец матрицы
являются одномерными массивами, которые также
принято называть вектором-строкой и векторомстолбцом соответственно.
13
14.
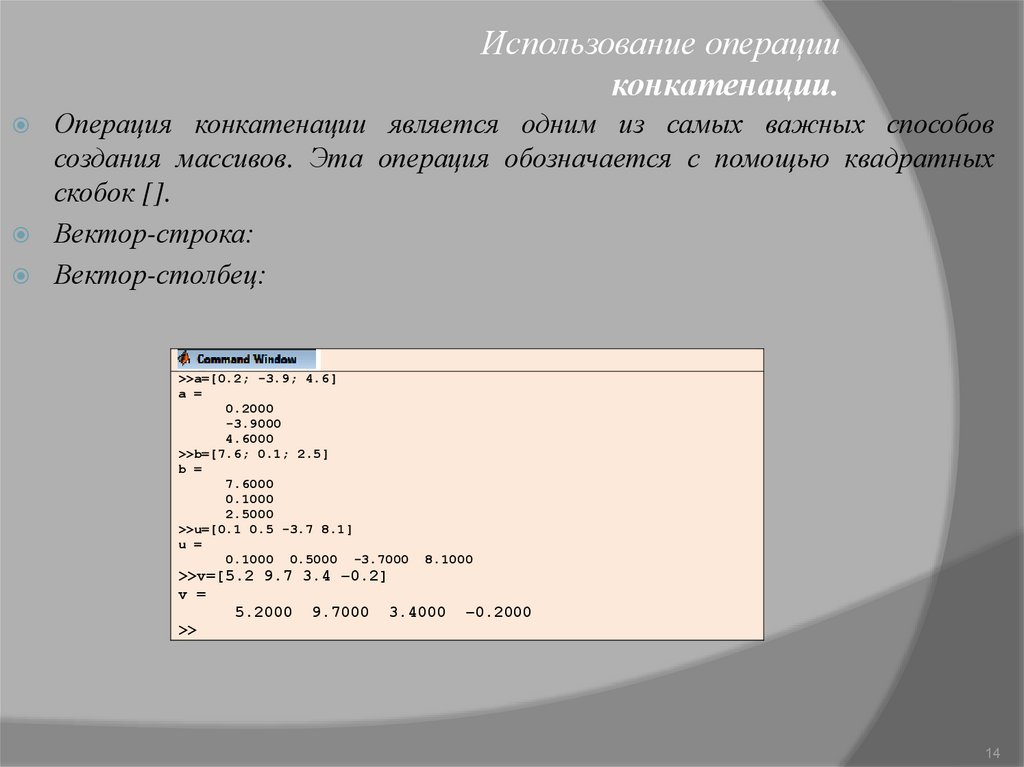
Использование операцииконкатенации.
Операция конкатенации является одним из самых важных способов
создания массивов. Эта операция обозначается с помощью квадратных
скобок [].
Вектор-строка:
Вектор-столбец:
>>a=[0.2; -3.9; 4.6]
a =
0.2000
-3.9000
4.6000
>>b=[7.6; 0.1; 2.5]
b =
7.6000
0.1000
2.5000
>>u=[0.1 0.5 -3.7 8.1]
u =
0.1000 0.5000 -3.7000
8.1000
>>v=[5.2 9.7 3.4 –0.2]
v =
5.2000 9.7000 3.4000
>>
–0.2000
14
15.
Использование операцииконкатенации.
Задание матрицы требует указания нескольких строк. Для разграничения
строк используется знак ; (точка с запятой).
>>A=[0.7 -2.5 9.1
8.4 0.3 1.7
-3.5 6.2 4.7]
A =
0.7000
-2.5000
8.4000
0.3000
-3.5000
6.2000
>>
9.1000
1.7000
4.7000
>>B=[6.1 0.3; -7.9 4.4; 2.5 -8.1]
B =
6.1000
0.3000
-7.9000
4.4000
2.5000
-8.1000
>>
>> C=[[0.4; 0.1] [-7.2; -2.1] [5.3; -9.5]]
C =
0.4000
-7.2000
5.3000
0.1000
-2.1000
-9.5000
>>
15
16.
Использование операциииндексации.
Для доступа к индивидуальному элементу одномерного массива нужно применить
операцию индексации, для чего после его имени указать в круглых скобках индекс
(т.е. номер) элемента.
Для указания отдельного элемента матрицы M используется выражение вида
M(k,m), где k,m обозначают номер строки и столбца соответственно.
Операция индексации позволяет непосредственно задавать элементы векторов и
матриц. Если нужно присвоить элементу M(k,m) новое значение х, следует
использовать выражение M(k,m)=x
Выражение M(k) с одним индексом дает доступ к элементам матрицы,
развернутым в один столбец. Такая матрица образуется из исходной, если подряд
выписать ее столбцы. Следующий пример поясняет такой доступ к элементам
матрицы M:
>> M=[1 2 3; 4 5 6; 7 8 9]
M=
1 2 3
4 5 6
7 8 9
>> M(2)
ans =
4
>> M(9)
ans =
9
>> M(5)=100;
>> M
M=
1 2
3
4 100 6
7 8 9
16
17.
Использованиеоператора :
Очень часто необходимо произвести формирование упорядоченных
числовых последовательностей или задание диапазона значений. Для
этого используется оператор : (двоеточие) – один из наиболее важных
операторов в MATLAB. Общий синтаксис использования этого оператора
имеет вид:
Начальное_значение:Шаг:Конечное_значение
Для формирования вектор строк :
>>x=-1.2:0.5:1.8
x =
-1.2000 -0.7000
-0.2000
0.3000
0.8000
1.3000
1.8000
>>n=-3:4
n =
-3 -2 -1 0 1 2 3 4
>>
>>x=10:-2:0
x =
10
8
6
4
2
0
17
18.
Генерирование матрицMATLAB имеет функции, которые позволяют создавать
матрицы с заданными свойствами. Ниже приводятся примеры
несколько таких функций
Функция
Результат и примеры вызовов
zeros
Нулевая матрица
F=zeros(4,5) F=zeros(3) F=zeros([3 4])
eye
Единичная прямоугольная матрица (единицы расположены на
главной диагонали)
I=eye(5,8) I=eye(5) I=eye([5 8])
ones
Матрица, целиком состоящая из единиц
E=ones(3,5) E=ones(6) E=ones([2 5])
rand
Матрица, элементы которой — случайные числа, равномерно
распределенные на интервале (0,1)
R=rand(5,7) R=rand(6) R=rand([3 5])
randn
Матрица, элементы которой — случайные числа, распределенные
по нормальному закону с нулевым средним и дисперсией, равной
единице N=randn(5,3) N=randn(9) N=randn([2 4])
diag
1) диагональная матрица, элементы которой задаются во входном
аргументе – векторе D=diag(v)
2) диагональная матрица со смещенной на k позиций диагональю
(положительные k — смещение вверх, отрицательные — вниз),
результатом является квадратная матрица
размера length(v)+abs(k) D=diag(v,k)
3) выделение главной диагонали из матрицы в вектор d=diag(A)
4) выделение k-ой диагонали из матрицы в вектор d=diag(A,k)
magic
задает магическую матрицу размера 5х5, у которой сумма всех
столбцов, всех строк и даже диагоналей равна одному и тому же
числу
a5=magic(5)
18
19.
Операции над массивамиАрифметические операции
+ Сложение. При сложении матрицы должны иметь одинаковые размеры. К матрице
любого размера можно прибавлять скаляр.
- Вычитание. При вычитании матрицы должны иметь одинаковые размеры. Из
матрицы любого размера можно вычитать скаляр.
* Матричное умножение. Число столбцов первого сомножителя равно числу строк
второго.
/ Деление матриц. A/B эквивалентно A*inv(B), inv - функция для вычисления обратной
матрицы.
\ Левое деление. A\B эквивалентно inv(A)*B. Результатом операции A\B является
решение системы линейных уравнений A*X=B.
^ Возведение в степень. Вычисление целой степени квадратной матрицы.
' Транспонирование матриц. Если матрица комплексная, то выполняется
транспонирование и комплексное сопряжение.
Поэлементные операции:
.* Поэлементное умножение. Матрицы должны иметь одинаковые размеры.
./ Поэлементное деление. Матрицы должны быть одинаковых размеров.
.\ Поэлементное левое деление. Матрицы должны быть одинаковых размеров.
.^ Поэлементное возведение в степень. Матрицы должны быть одинаковых размеров.
.' Транспонирование матрицы. (Без комплексного сопряжения).
19
20.
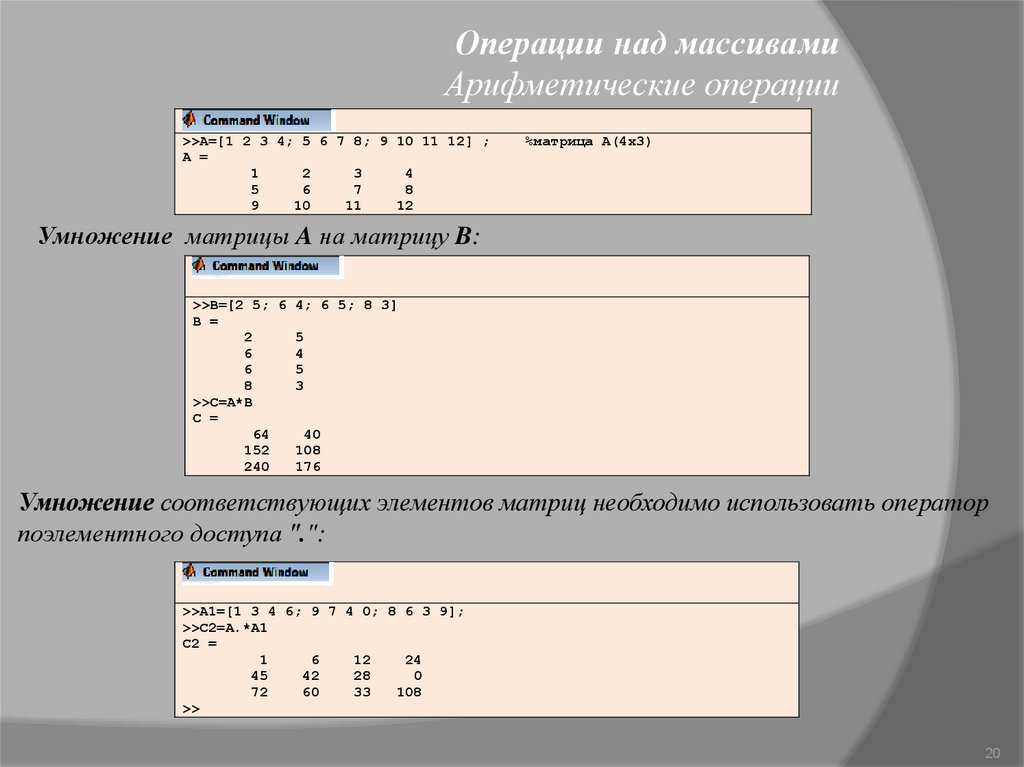
Операции над массивамиАрифметические операции
>>A=[1 2 3 4; 5 6 7 8; 9 10 11 12] ;
A =
1
2
3
4
5
6
7
8
9
10
11
12
%матрица А(4х3)
Умножение матрицы A на матрицу B:
>>B=[2 5; 6 4; 6 5; 8 3]
B =
2
5
6
4
6
5
8
3
>>C=A*B
C =
64
40
152
108
240
176
Умножение соответствующих элементов матриц необходимо использовать оператор
поэлементного доступа ".":
>>A1=[1 3 4 6; 9 7 4 0; 8 6 3 9];
>>С2=A.*A1
С2 =
1
6
12
24
45
42
28
0
72
60
33
108
>>
20
21.
Операции над массивамиАрифметические операции
Добавление элементов ("увеличение матрицы"):
>>a1=[A;x]
a1 =
1
5
9
1
2
6
10
2
3
7
11
3
4
8
12
4
>>
Транспонирование матрицы (апостроф - ' ):
>>Bt=B'
Bt =
2
5
6
4
6
5
8
3
>>
Удаление строки (столбца матрицы), в примере удален второй столбец:
>>A(:,2)=[ ]
A =
1
3
5
7
9
11
%круглые скобки – оператор извлечения
4
8
12
>>
21
22.
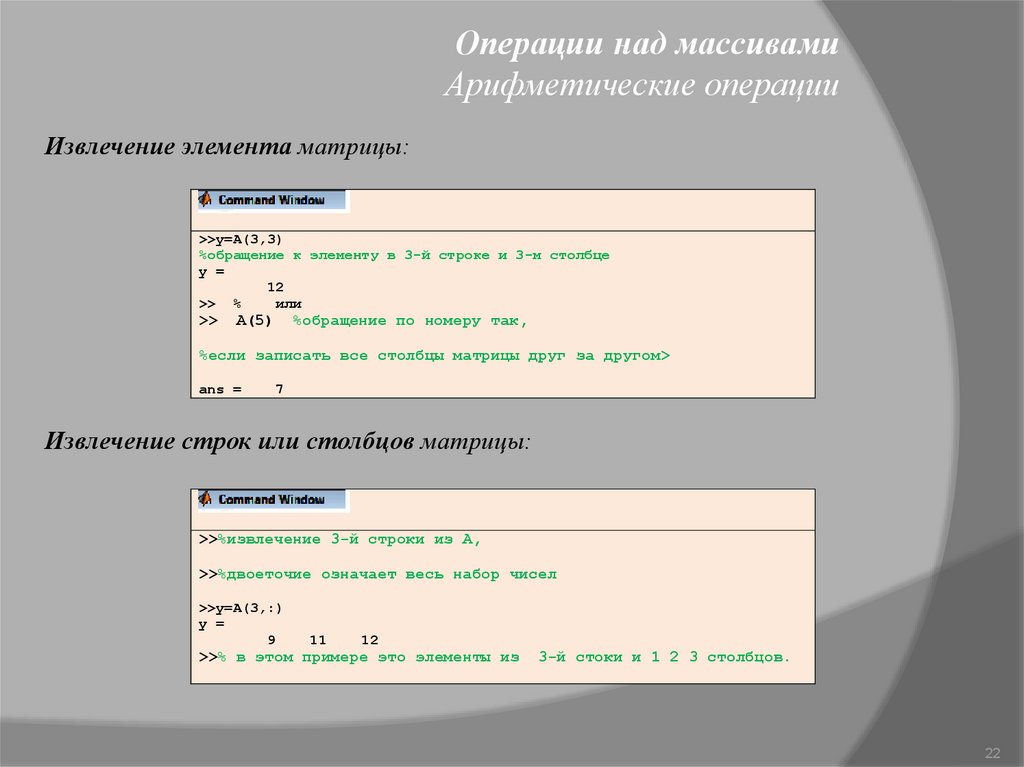
Операции над массивамиАрифметические операции
Извлечение элемента матрицы:
>>y=A(3,3)
%обращение к элементу в 3-й строке и 3-м столбце
y =
12
>> %
или
>>
A(5)
%обращение по номеру так,
%если записать все столбцы матрицы друг за другом>
ans =
7
Извлечение строк или столбцов матрицы:
>>%извлечение 3-й строки из А,
>>%двоеточие означает весь набор чисел
>>y=A(3,:)
y =
9
11
12
>>% в этом примере это элементы из
3-й стоки и 1 2 3 столбцов.
22
23.
Операции над массивамиВычисление функций от массивов
>>x=-1.2:0.5:1.8
x =
-1.2000 -0.7000 -0.2000
>>f=(x.*sin(x)+x.^2)./(x+1)
f =
-12.7922 3.1365
0.0997
>>
0.3000
0.1374
0.8000
0.6744
1.3000
1.8000
1.2794
1.7832
Как отмечалось, принадлежность MATLAB к матричным системам
вносит коррективы в назначение операторов. Рассмотрим пример:
>> х=0:5
х=
012345
>> cos(х)
ans =
1.0000 0.5403 -0.4161 -0.9900 -0.6536 0.2837
>> sin(х)/х
ans =
>> sin(x)./х
-0.0862
Warning: Divide by zero.
ans =
NaN 0.8415 0.4546 0.0470 -0.1892 -0.1918
23
24.
Операции над массивамиФункции для работы с матрицами
Полный список таких функций можно непосредственно получить, используя
команды help datafun и help elmat.
Функции
Назначение
s=sum(a)
Сумма всех элементов вектора a
p=prod(a)
Произведение всех элементов вектора a
m=max(a)
Нахождение максимального значения среди элементов вектора a
[m,k]=max(a)
Второй выходной аргумент k содержит номер максимального
элемента в векторе a
m=min(a)
Нахождение минимального значения среди элементов вектора a
[m,k]=min(a)
Второй выходной аргумент k содержит номер минимального
элемента в векторе a
m=mean(a)
Вычисление среднего арифметического элементов вектора a
a1=sort(a)
Упорядочение элементов вектора a по возрастанию
[a1,ind]=sort(a) Второй выходной аргумент ind является вектором из целых чисел
от 1 до length(a), который соответствует проделанным
перестановкам
length(v)
длина вектора v;
size(A)
размер матрицы A;
diag(A)
выделение главной диагонали матрицы A;
24

















 Математика
Математика Программирование
Программирование








