Похожие презентации:
Методы целочисленного линейного программирования
1.
Методы целочисленноголинейного
программирования
Подготовили:
Дральщиков Н.С.
Зайцев Е.С.
Кирейченков Н.С.
Преподаватель: Новицкий В.О.
2.
Целочисленное линейноепрограммирование
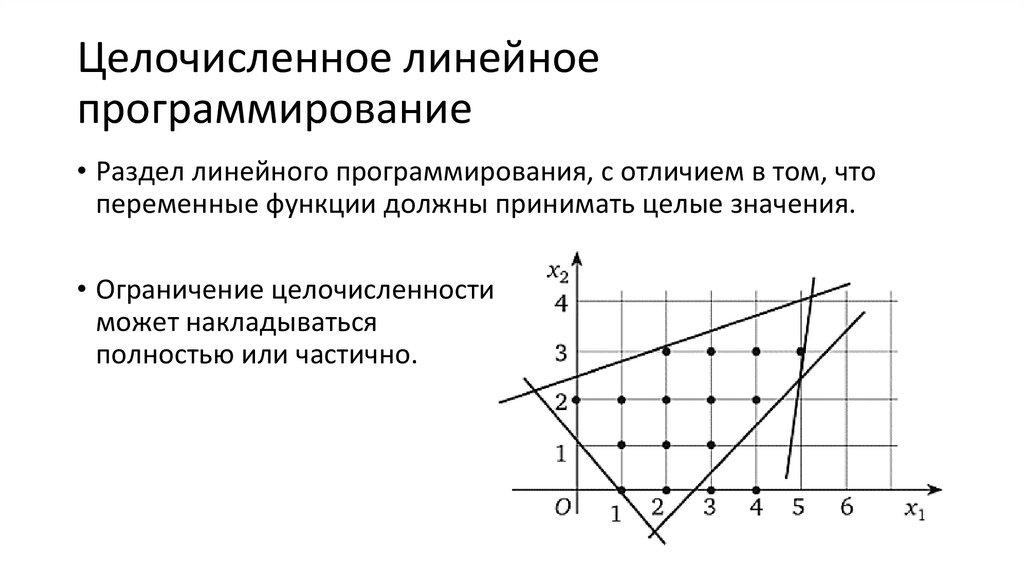
• Раздел линейного программирования, с отличием в том, что
переменные функции должны принимать целые значения.
• Ограничение целочисленности
может накладываться
полностью или частично.
3.
Задачи ЦЛП – Задача о рюкзаке• Представим себе путешественника, который собирает в дорогу
рюкзак. В его распоряжении n предметов. Пусть известны
вес aj и «ценность» cj каждого предмета (j = 1, 2, . . . , n).
Требуется заполнить рюкзак, не превышая его грузоподъемности
b и максимизируя суммарную ценность груза.
• Получаем следующую булеву ЗЦЛП (задача о {0, 1}-рюкзаке):
4.
Задачи ЦЛП – Задача о рюкзаке• Предположим теперь, что каждый предмет имеется в
неограниченном числе экземпляров, и требуется также
максимизировать суммарную ценность груза, не превышая
грузоподъемности. Получаем так называемую задачу о
целочисленном рюкзаке:
5.
Задачи ЦЛП – Задача коммивояжера• Коммивояжер должен посетить n городов, не побывав ни в
одном дважды, и в конце возвратиться в исходный город.
Предположим, что известны все расстояния aij между любыми
двумя городами i и j (i = 1, . . . , n; j = 1, . . . , n). Каков должен быть
маршрут коммивояжера, чтобы суммарное расстояние,
пройденное им, было минимальным?
• Известно несколько способов сведения этой задачи к ЗЦЛП.
Рассмотрим способ, принадлежащий Таккеру.
6.
Задачи ЦЛП – Задача коммивояжера• Определим переменные xij следующим образом:
7.
Задачи ЦЛП – Задача коммивояжера• Из каждого города коммивояжер должен выехать ровно один раз,
поэтому
• В каждый город коммивояжер должен въехать ровно один раз,
поэтому:
• Однако, таких условий не достаточно.
8.
Задачи ЦЛП – Задача коммивояжера• Чтобы отбросить такие случаи, Таккер предложил ограничения
дополнить n · (n − 1) неравенствами вида:
где xi — новые вещественные переменные.
• Итак, задача коммивояжера состоит в минимизации
функции
при ограничениях выше.
9.
Задачи ЦЛП – Дихотомии• Пусть среди ограничений некоторой задачи математического
программирования есть условия-дихотомии вида:
или
где G1, G2 — некоторые функции. Предположим, что известны
нижние границы g1, g2 для значений этих функций:
10.
Задачи ЦЛП – Дихотомии• Тогда, введя новую целочисленную переменную y,
удовлетворяющую условиям:
сведем условия к системе линейных неравенств:
• Если остальные ограничения являются линейными, а также
линейными являются функции G1 и G2, то полученная задача
является ЗЦЛП.
11.
Задачи ЦЛППомимо указанных, существуют еще следующие задачи
целочисленного линейного программирования:
• Задачи о выполнимости КНФ
• Задача о «раскрое»
• Задача коммивояжера
12.
Различия методов ЛП и ЦЛПМетоды линейного программирования (ЛП) и методы целочисленного линейного
программирования (ЦЛП) имеют общие основы, но существенные отличия в том,
как они решают оптимизационные задачи. Линейное программирование
работает с непрерывными переменными, которые могут принимать любые
действительные значения в заданных диапазонах, в то время как целочисленное
линейное программирование работает с переменными, ограниченными целыми
числами. Это означает, что решения в ЦЛП должны быть целыми числами, что
ограничивает множество допустимых решений.
• Когда решения в ЦЛП ограничены целыми числами, это усложняет процесс
поиска оптимального решения. Решение задач ЦЛП требует более сложных
методов, таких как метод ветвей и границ, что может привести к значительному
увеличению вычислительной сложности по сравнению с ЛП. Линейное
программирование имеет эффективные методы решения, такие как симплексметод, и обычно может быть решено быстро для большинства задач.
• Методы ЦЛП берут основу из ЛП и используют такие подходы из симплексметода и графического метода.
13.
Методы отсеченияСуть методов состоит в том, что сначала решается задача линейного
программирования без условия целочисленности. Если полученный
ответ удовлетворяет условию целочисленности, то задача решена. В
противном случае к ограничениям задачи добавляется новое
ограничение.
После введения нового ограничения вновь решается задача линейного
программирования. Если вновь полученный план целочисленный, то
задача решена. Если это не так, то к задаче добавляется новое
ограничение. Процесс повторяется до тех пор, пока полученный
оптимальный план не будет полностью целочисленным.
Геометрический смысл добавления новых ограничений – это
проведение дополнительной прямой, которая отсекает от
многоугольника его часть решений с нецелыми координатами.
14.
Алгоритм ГомориЭтапы работы алгоритма Гомори:
• Решение задачи линейного программирования без учета
целочисленности
• Выбор дробного элемента и составление ограничений
• Преобразованная задача решается симплекс-методом
15.
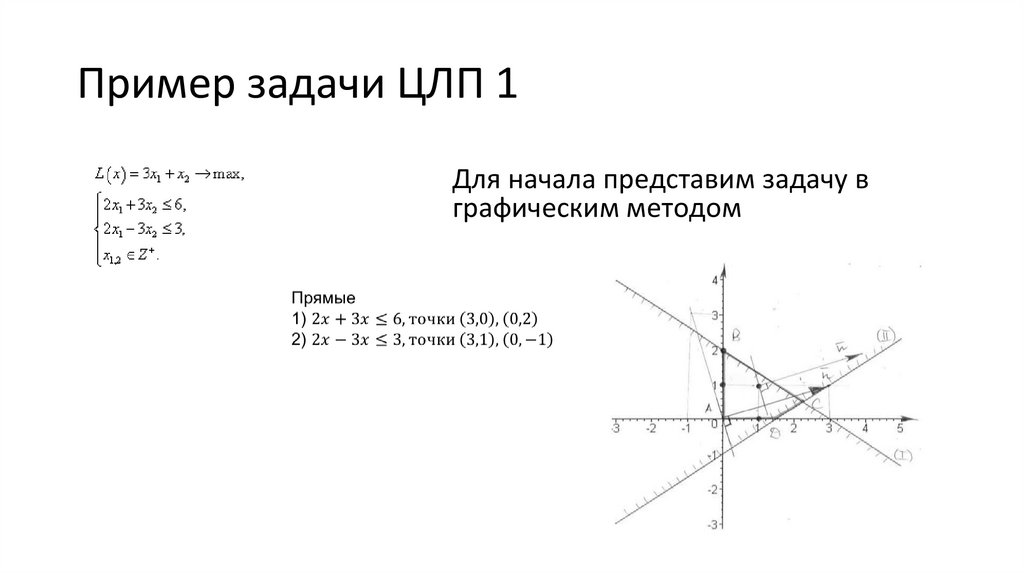
Пример задачи ЦЛП 1Для начала представим задачу в
графическим методом
16.
Пример решения методом ГомориБазис
B
x1
x2
x3
x4
x3
21
5
7
1
0
x4
8
-1
3
0
1
F(X0)
0
-1
-2
0
0
17.
18.
На основе новых ограничений строим симплекс-таблицу
Решение нецелочисленно, вводим новое ограничение
целочисленности
Решение нецелочисленно, вводить ограничения, следует до
момента пока оптимальное решение не станет целочисленным.
19.
20.
Особенность метода ГомориПрименение дробного отсечения предполагает
целочисленность всех переменных, включая дополнительные.
Это значит, что данный метод применим только к решению
полностью целочисленных задач, для решения частично
целочисленных задач линейного программирования можно
использовать метод ветвей и границ
21.
Метод ветвей и границ• Суть метода заключается в поиске оптимального решения задачи
целочисленного линейного программирования путём разбиения
задачи на более мелкие подзадачи и эффективного поиска в
пространстве возможных решений.
• Основные концепции метода – ветвление и поиск границ.
• Если в результате получено оптимальное нецелочисленное
решение, ОДР подзадачи снова разбивается на части и этот
процесс продолжается до тех пор, пока не будет найдено
оптимальное целочисленное решение исходной задачи.
22.
Пример задачи ЦЛП 2Воспользуемся методом ветвей и границ для решения этой
ЗЦЛП
Для начала, составляем первую симплекс-таблицу
23.
24.
Данная задача имеет нецелочисленный оптимальный план
Эта задача не имеет решения
Теперь рассматриваем задачу 1, которая имеет решение, и, аналогично
предыдущему случаю, разбиваем ее на две задачи. Выбираем переменную с
дробным значением с x2 = 51/22. Разбиваем задачу на две подзадачи
(учитывая, что [51/ 22] 2 = , в одной полагаем x2 ≤ 2 , в другой – x2 ≥ 3.
Решаем обе задачи.
25.
Задача 1-1, имеет нецелочисленный оптимальный план
Данная задача имеет нецелочисленный оптимальный план
Так как задача 1-1 имеет значение целевой функции больше, чем
задача 1-2, разбиваем её на две подзадачи. Выбираем переменную с
дробным значением с x3 =1/ 8 . Разбиваем задачу на две подзадачи
(учитывая, что [1/8] = 0 , в одной полагаем x3 ≤ 0 , в другой – x3 ≥1.
26.
Данная задача имеет целочисленный оптимальный план.
Задача 1-1-2 имеет целочисленный оптимальный план.
27.
Оптимальное целочисленное решениеДерево решений задачи
28.
Графический метод• Графический метод является одним из способов решения задачи
целочисленного линейного программирования, когда
переменные ограничены целыми числами. Этот метод особенно
полезен, когда есть только две переменные (двумерное
пространство), так как он позволяет визуально представить
решение задачи.
• Графический метод является хорошим способом начать решение
задачи ЦЛП с двумя переменными, но может быть
неэффективным для задач с более чем двумя переменными или
сложными ограничениями.



























 Программирование
Программирование








