Похожие презентации:
Метод Гомори решения задач ЦЛП. Лекция 8
1. Метод Гомори решения задач ЦЛП
Лекция 81
2. План лекции
I Постановка задачи ЦЛП в общем видеII Алгоритм метода Гомори
III Пример реализации
2
3. Общая постановка ЗЦЛП
Целевая функцияn
F x с jx j max 1
j 1
Система ограничений
n
a ijx j bi , i 1, m 2
j 1
x j 0, j 1, n
3
x j Z (целые) j 1, k , k n 4
Если k<n задача частичноцелочисленная
Если k=n задача полностью целочисленная
3
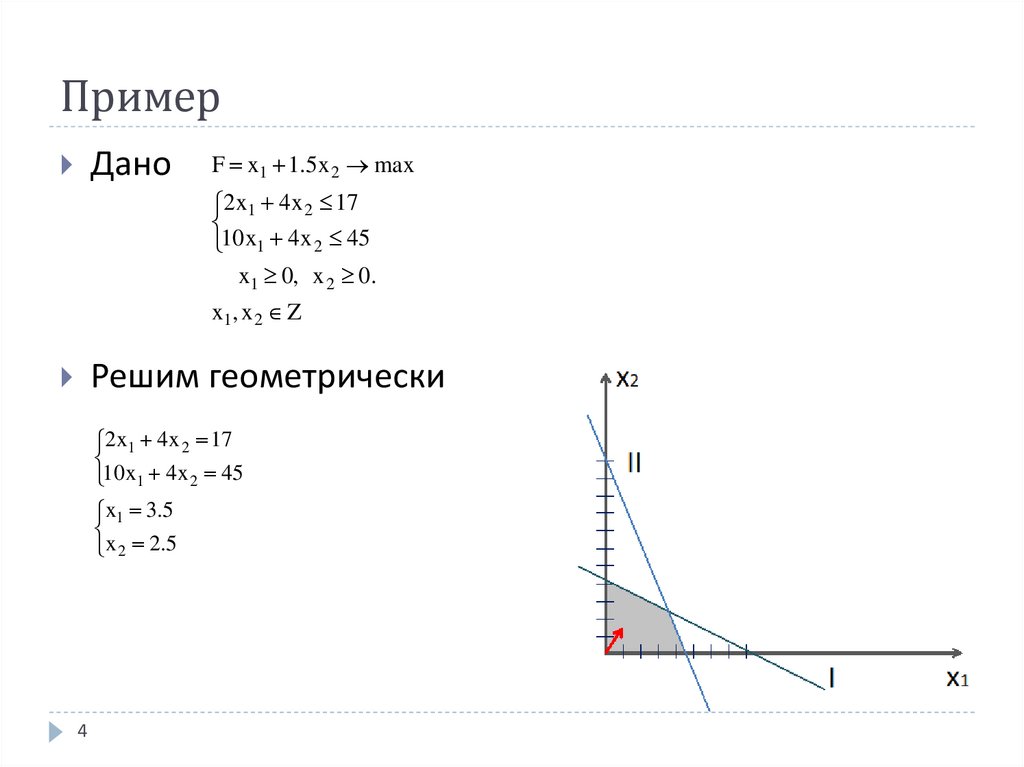
4. Пример
ДаноF x1 1.5x 2 max
2 x1 4 x 2 17
10 x1 4 x 2 45
x1 0, x 2 0.
x1, x 2 Z
Решим геометрически
2 x1 4 x 2 17
10 x1 4 x 2 45
x1 3.5
x 2 2 .5
4
5. Алгоритм метода Гомори
1. Решаем задачу ЛП (1- 3) симплекс-методом.2. Полученное оптимальное решение задачи (1-3), если оно
существует, проверяем на целочисленность:
если все xj, допустимые целые, то, полученное оптимальное
решение задачи ЛП является оптимальным решением задачи
целочисленного программирования, конец алгоритма;
если задача ЛП решения не имеет, то не имеет решения и задача
целочисленного программирования;
наконец, если хотя бы одна координата не удовлетворяет условию
(4), то переходим к шагу 3.
3. Строим дополнительное линейное ограничение, с помощью
которого отсекается та часть допустимой области,
определяемой условиями (2-3), в которой содержится
оптимальное решение задачи ЛП (1-3), но нет ни одного
допустимого решения, удовлетворяющего условию (4) и вновь
выполняем пункт 1 для задачи ЛП с дополнительным
ограничением.
5
6. Построение отсечения
Гомори показал, что при «k-м" возвращении к решениюзадачи ЛП, “k-е" дополнительное ограничение имеет
вид:
x n k 1 x i0 x i0
x ij x ij x j ,
j I s
k 0,1,2,..., x n k 1 0
5
где [xi0], [xij] – целая часть соответствующей величины;
xi0 – нецелая координата оптимального плана задачи (13) у которой нецелая часть самая большая;
xij – координаты разложения векторов Аj, не попавших в
базис;
Is – множество векторов, не попавших в базис
6
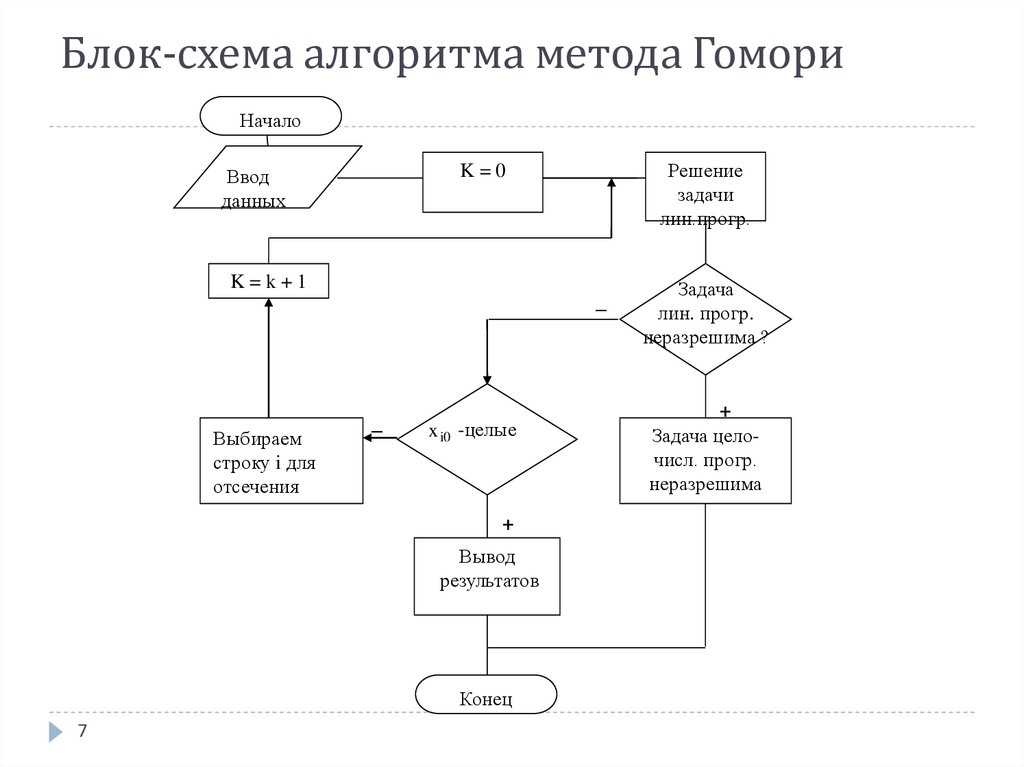
7. Блок-схема алгоритма метода Гомори
НачалоРешение
задачи
лин.прогр.
K=0
Ввод
данных
K=k+1
–
Выбираем
строку i для
отсечения
–
x i0 -целые
+
Вывод
результатов
Конец
7
Задача
лин. прогр.
неразрешима ?
+
Задача целочисл. прогр.
неразрешима
8. Расчетные формулы для построения отсечения
Ограничение (5) может быть записано в виде:1) отсечение для целочисленной задачи ЛП
x ij x j x i0 (6)
j I s
2) отсечение для частично целочисленной задачи
ijx j x i0 (7)
j I s
где коэффициенты зависит от типа переменной:
а) для переменных, которые могут быть нецелыми
x ij ,
ij x i 0
1 x x ij ,
i0
8
x ij 0
x ij 0
8
б) для переменных, которые должны быть целые
x ij x i 0
x ij ,
ij 1 x ij
1 x x i 0 , x ij x i 0
i0
9. Пример
ДаноF x1 x 2 max
x 1 2 .5
x 2 2 .5
x1 0, x 2 0.
x1 , x 2 Z
Канонический вид
F x1 1x 2 max
x1 x 3 2,5
x 2 x 4 2,5
x1 0, x 2 0, x 3 0, x 4 0
x1 , x 2 Z
9
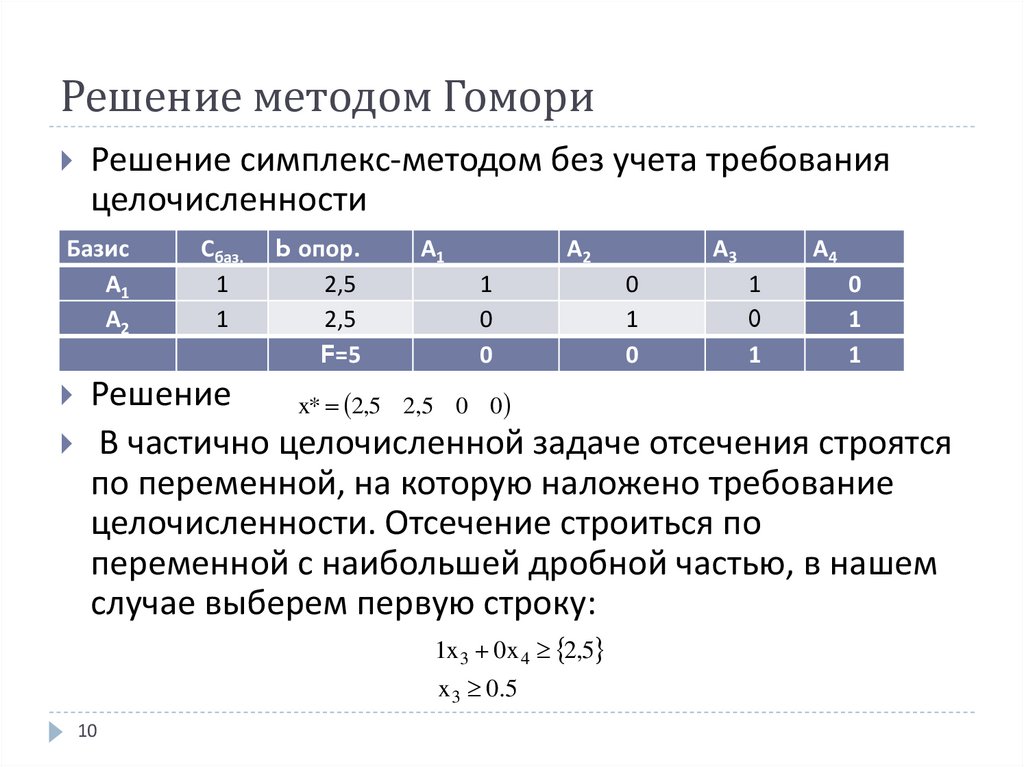
10. Решение методом Гомори
Решение симплекс-методом без учета требованияцелочисленности
Базис
А1
А2
Сбаз.
1
1
b опор.
2,5
2,5
F=5
А1
А2
1
0
0
А3
0
1
0
А4
1
0
1
0
1
1
Решение
x* 2,5 2,5 0 0
В частично целочисленной задаче отсечения строятся
по переменной, на которую наложено требование
целочисленности. Отсечение строиться по
переменной с наибольшей дробной частью, в нашем
случае выберем первую строку:
1x 3 0x 4 2,5
x 3 0 .5
10
11. Решение методом Гомори. Вторая итерация
Выразим фиктивную переменную x3 из первогоограничения и подставим его в полученное отсечение:
2.5 x1 0,5
x1 2
F x1 x 2 max
F x1 1x 2 max
x1 2,5
x 2 2,5
x 2
1
x1 0, x 2 0.
x1 x 3 2
x 2 x 4 2,5
x1 0, x 2 0, x 3 0, x 4 0
x1 , x 2 Z
x1, x 2 Z
Решаем симплекс-методом
Базис
А1
А2
11
Сбаз.
1
1
b опор.
2
2,5
F=4,5
А1
1
0
0
x* 2 2,5 0 0
А2
0
1
0
А3
1
0
1
А4
0
1
1
12. Решение методом Гомори. Третья итерация
Построение отсечения0 x 3 1x 4 2,5
x 4 0 .5
Выражаем фиктивную переменную
2.5 x 2 0,5
x2 2
F x1 x 2 max
F x1 1x 2 max
x1 2
x 2 2,5
x 2
2
x1 0, x 2 0.
x1 x 3 2
x 2 x 4 2
x1 0, x 2 0, x 3 0, x 4 0
x1 , x 2 Z
x1, x 2 Z
Базис
А1
А2
12
Сбаз.
1
1
b опор.
2
2
F=4
А1
1
0
0
А2
0
1
0
А3
1
0
1
А4
0
1
1
13. Задание на практику
Решить методом Гомори примерF x1 1.5x 2 max
2 x1 4 x 2 17
10 x1 4 x 2 45
x1 0, x 2 0.
x1, x 2 Z
13









 Программирование
Программирование








